0106广度优先搜索和最短路径-无向图-数据结构和算法(Java)
1 单点最短路径
单点最短路径。 给定一幅图和一个起点s,回答“从s到给定目的顶点v是否存在一条路径?如果有,找出其中最短的那条(所含边数最少)。“等类似问题。
深度优先搜索在这个问题上没有什么作为,因为它遍历整个图的顺序和找出最短路径的目标没有任何关系。相比之下,广度优先搜索正好可以解决这个问题。
分析:
- 要找的从s到v的最短路径,从s开始,在所有由一条边就可以到达的顶点中寻找v,找到标记结束。
- 如果没有找到,我们继续在于s距离2条边的顶点中查找v,如此一直进行。
- 最后也没有找到,那么说明s到给定顶点v不存在路径,此图为非连通图。
结构选择:
- 广度优先搜索中,我们希望按照与起点的距离顺序遍历所有顶点,所以我们选择队列(先入先出)。
2 广度优先搜索实现
实现代码如下:
package com.gaogzhen.datastructure.graph.undirected;import edu.princeton.cs.algs4.*;/*** 最短路径算法* @author: Administrator* @createTime: 2023/03/07 21:04*/
public class BreadthFirstDirectedPaths {private static final int INFINITY = Integer.MAX_VALUE;/*** 标记顶点是否与起点连通*/private boolean[] marked;/*** 表示顶点到与该顶点连通的顶点间最短路径*/private int[] edgeTo;/*** 顶点到起点之间的边数*/private int[] distTo;/*** 计算从指定顶点到起点最短路径* @param G 无向图* @param s 起点* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public BreadthFirstDirectedPaths(Graph G, int s) {marked = new boolean[G.V()];distTo = new int[G.V()];edgeTo = new int[G.V()];for (int v = 0; v < G.V(); v++) {distTo[v] = INFINITY;edgeTo[v] = -1;}validateVertex(s);bfs(G, s);}/*** 计算多个起点到指定顶点之间的最短路径* @param G 无向图* @param sources 多个起点集合* @throws IllegalArgumentException if {@code sources} is {@code null}* @throws IllegalArgumentException unless each vertex {@code v} in* {@code sources} satisfies {@code 0 <= v < V}*/public BreadthFirstDirectedPaths(Graph G, Iterable<Integer> sources) {marked = new boolean[G.V()];distTo = new int[G.V()];edgeTo = new int[G.V()];for (int v = 0; v < G.V(); v++) {distTo[v] = INFINITY;edgeTo[v] = -1;}validateVertices(sources);bfs(G, sources);}/*** 广度优先搜索从指定顶点到起点最短路径* @param G 无向图* @param s 起点*/private void bfs(Graph G, int s) {Queue<Integer> q = new Queue<Integer>();marked[s] = true;distTo[s] = 0;q.enqueue(s);while (!q.isEmpty()) {int v = q.dequeue();for (int w : G.adj(v)) {if (!marked[w]) {edgeTo[w] = v;distTo[w] = distTo[v] + 1;marked[w] = true;q.enqueue(w);}}}}// BFS from multiple sourcesprivate void bfs(Graph G, Iterable<Integer> sources) {Queue<Integer> q = new Queue<Integer>();for (int s : sources) {marked[s] = true;distTo[s] = 0;q.enqueue(s);}while (!q.isEmpty()) {int v = q.dequeue();for (int w : G.adj(v)) {if (!marked[w]) {edgeTo[w] = v;distTo[w] = distTo[v] + 1;marked[w] = true;q.enqueue(w);}}}}/*** 起点s与指定顶点v之间是否有路径(连通)* @param v the vertex* @return {@code true} if there is a directed path, {@code false} otherwise* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public boolean hasPathTo(int v) {validateVertex(v);return marked[v];}/*** 返回指定顶点v到起点直接的最短路径(边数)}?* @param v the vertex* @return the number of edges in such a shortest path* (or {@code Integer.MAX_VALUE} if there is no such path)* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public int distTo(int v) {validateVertex(v);return distTo[v];}/*** 返回指定顶点v到起点直接的最短路径,没有返回null* @param v the vertex* @return the sequence of vertices on a shortest path, as an Iterable* @throws IllegalArgumentException unless {@code 0 <= v < V}*/public Iterable<Integer> pathTo(int v) {validateVertex(v);if (!hasPathTo(v)) return null;Stack<Integer> path = new Stack<Integer>();int x;for (x = v; distTo[x] != 0; x = edgeTo[x])path.push(x);path.push(x);return path;}// throw an IllegalArgumentException unless {@code 0 <= v < V}private void validateVertex(int v) {int V = marked.length;if (v < 0 || v >= V)throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}// throw an IllegalArgumentException if vertices is null, has zero vertices,// or has a vertex not between 0 and V-1private void validateVertices(Iterable<Integer> vertices) {if (vertices == null) {throw new IllegalArgumentException("argument is null");}int V = marked.length;int count = 0;for (Integer v : vertices) {count++;if (v == null) {throw new IllegalArgumentException("vertex is null");}validateVertex(v);}if (count == 0) {throw new IllegalArgumentException("zero vertices");}}
}
队列保存所有已被标记但其邻接表未被检查过的顶点。先将起点加入队列,然后重复一下步骤知道队列为空。
- 取出队列中的下一个顶点v并标记它。
- 将与v相邻的所有未被标记过的顶点加入队列。
说明:
- edgeTo[]数组结果,也是一棵用父链接表示的根结点为s的树
- 多起点中,则以各自起点为根结点的树组成的森林。
- distTo[]表示到起点的路径长度,即边数。代码distTo[w] = distTo[v] + 1;当前顶点路径长度为其父顶点路径长度+1,起点为0。
- 与算法第四版不同的地方只是在初始化edgeTo为-1表示根结点;算法第四版默认都是0。
以之前无向图(6个顶点,8条边)为例单起点搜索索引起点为0(单起点的路径结果:

多起点(0,2)搜索结果如下图所示:

多起点搜索很少用到,一般情况下我们讨论最短路径默认为单点最短路径。
3 总结
命题B。对于从s可达的任意顶点v,广度优先搜索都能找到一条从s到v的最短路径(没有其他从s到v的路径所含有的边比这条路径少。
证明:由归纳易得队列总是包含林哥或者多个到起点的距离为k的顶点,之后是零个或者多个到起点为k+1的顶点,k为整数,起始值为0.这意味着顶点是按照它们和s的距离顺序加入或者离开队列。从顶点v加入队列到它离开队列之前,不可能找出到v的更短路径,而在v离开队列之后发现的所有能够到达v的路径都不可能短于v在树中的路径长度。
命题B(续)。广度优先搜索所需的时间在最坏情况下和V+E成正比。
证明:广度优先搜索标记所有与s连通的顶点所需的时间与它们的度数之和成正比。如果图是连通的,这个和就是所有顶点的度数之和,也就是2E。
广度优先搜索也可以解决单点连通问题,它检查所有与起点连通的顶点和边的方法取决于查找的能力。代码如下:
private void bfs(Graph G, int s) {Queue<Integer> q = new Queue<Integer>();marked[s] = true;q.enqueue(s);while (!q.isEmpty()) {int v = q.dequeue();for (int w : G.adj(v)) {if (!marked[w]) {marked[w] = true;q.enqueue(w);}}}
}
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p344-348.
相关文章:

0106广度优先搜索和最短路径-无向图-数据结构和算法(Java)
1 单点最短路径 单点最短路径。 给定一幅图和一个起点s,回答“从s到给定目的顶点v是否存在一条路径?如果有,找出其中最短的那条(所含边数最少)。“等类似问题。 深度优先搜索在这个问题上没有什么作为,因为…...

僵尸(Zombie)进程
文章目录1.僵尸进程2.产生僵尸进程的原因3.利用 wait 函数销毁僵尸进程4.使用 waitpid 函数销毁僵尸进程1.僵尸进程 进程完成工作后(执行完 main 函数中的程序后)应被销毁,但有时这些进程将变成僵尸进程,占用系统中的重要资源。这…...
JS实现:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?
题目:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少? 数列是 1,1,2,3,5,8,13,21....观察可以看出来从第三个数字开始…...

Verilog如何编写一个基础的Testbench
本文将讲述如何使用Verilog 编写一个基础的测试脚本(testbench)。在考虑一些关键概念之前,先来看看testbench的架构是什么样的。架构包括建模时间、initial块(initial block)和任务(task)。此文…...
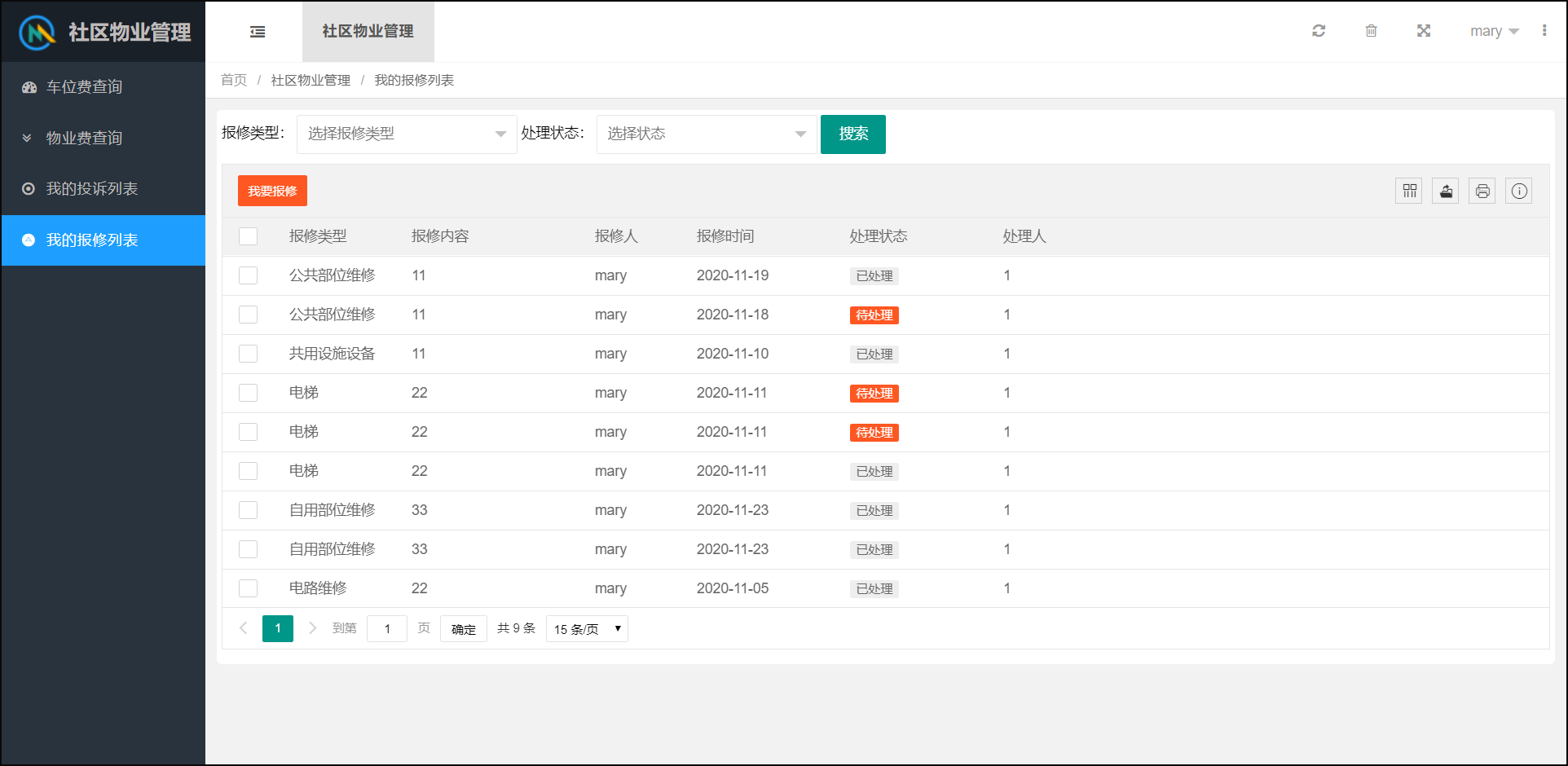
基于JavaEE社区物业管理系统开发与实现(附源码资料)
文章目录1. 适用人群2. 你将收获3.项目简介4.技术栈5.测试账号6.部分功能模块展示6.1.管理员6.2.业主1. 适用人群 本课程主要是针对计算机专业相关正在做毕业设计或者是需要实战项目的Java开发学习者。 2. 你将收获 提供:项目源码、项目文档、数据库脚本、软件工…...
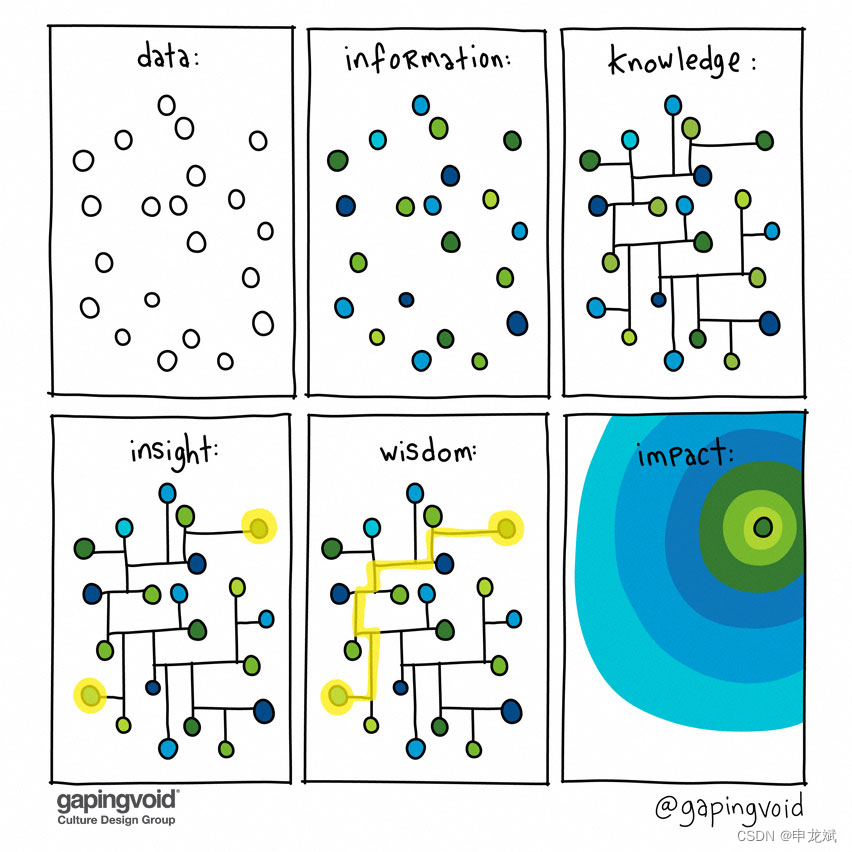
问一下ChatGPT:DIKW金字塔模型
经常看到这张DIKW金字塔模型图,还看到感觉有点过份解读的图,后面又加上了insight,impact等内容。 Data:是数据,零散的、无规则的呈现到人们眼前,如果你只看到这些数字,如果没有强大的知识背景&a…...

javaScript基础面试题 ---闭包
闭包1、闭包是什么?2、闭包可以解决什么问题?3、闭包的缺点1、闭包是什么? 闭包是一个函数加上到创建这个函数的作用域的链接,就是一个作用域可以访问到另一个作用域的变量,闭包‘关闭’了函数的自由变量 function f…...
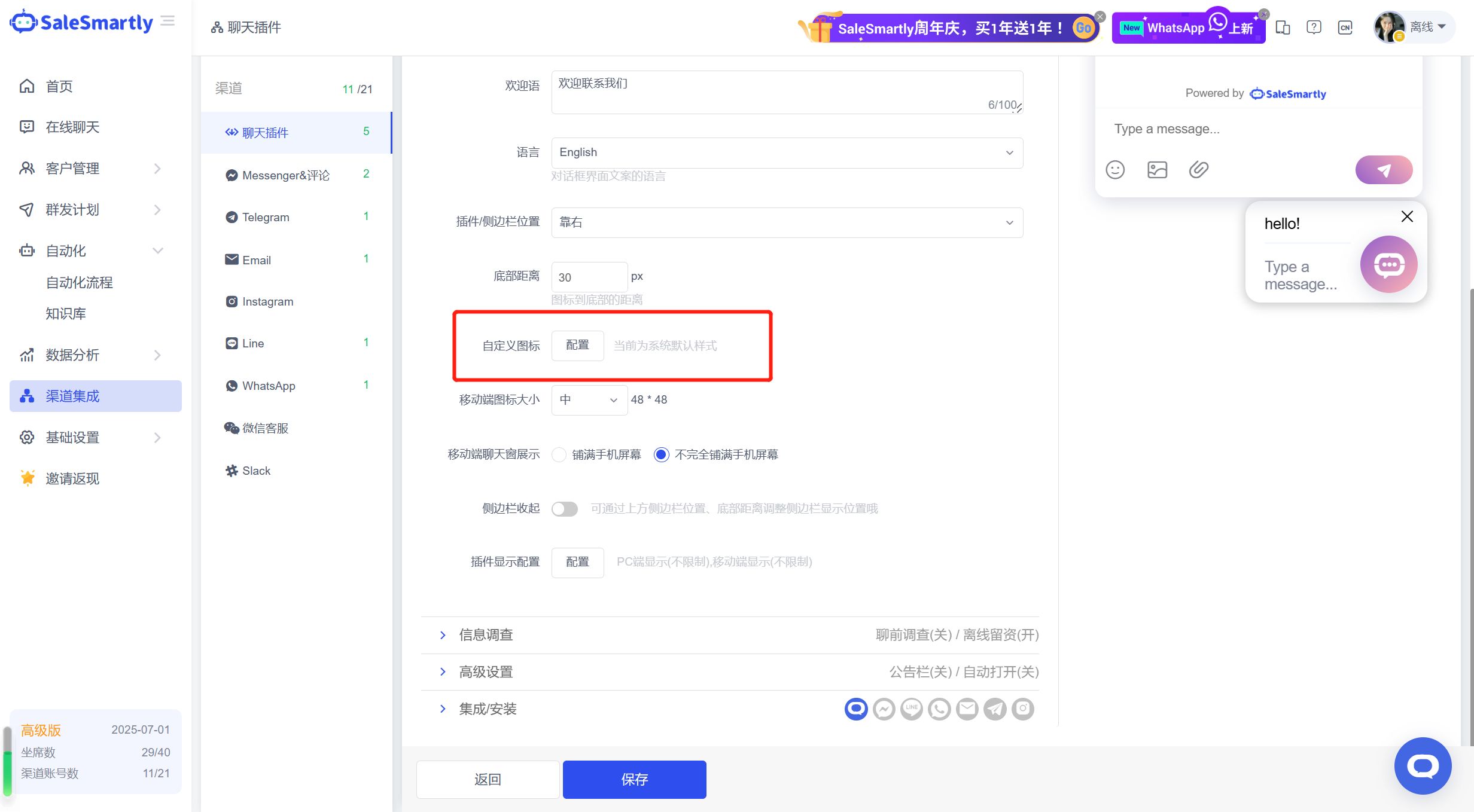
如何自定义您的网站实时聊天图标
实时聊天图标是您网站上的一个按钮,可在访问者单击时打开实时聊天。它代表了您的企业与客户沟通的门户。这是您的网站访问者与您联系、提出问题和接收个性化推荐的一种方式,聊天图标的设计最好是简单且引人入胜,个性化的图标往往更能提现企业…...

Vue侦听器Watch
31. Vue侦听器Watch 1. 定义 Watch是Vue.js提供的一个观察者模式,用于监听数据的变化并执行相应的回调函数。虽然计算属性Computed在大多数情况下更合适,但有时也需要一个自定义的侦听器Watch。因为在有些情况下,我们需要在状态变化时执行一…...

云快充研发中心平台架构师谈云原生稳定性建设之路
作者:吕周洋 大家好,我是来自云快充研发中心的平台架构师吕周洋,今天我给大家分享云快充云原生稳定性之路。 点击查看:云快充研发中心平台架构师 吕周洋:云快充云原生稳定性治理之路 云快充成立于2016年,…...
ENVI IDL学习笔记之基本操作
前言ENVI IDL(交互式数据语言)是一个通用的科学计算包,它提供了一套数学函数、数据分析工具,以及一些科学可视化和动画工具。IDL 是 ENVI 图像处理和分析软件的基础,可用于编写脚本并自动执行许多使用 ENVI 图形用户界…...

多线程面试题
1. Sychronized的锁升级过程是怎样的? 2. Tomcat 中为什么要使用自定义类加载器? 3. 说说对线程安全的理解 4. 对守护线程的理解 5. 并发、并行、串行之间的区别 6. Java死锁如何避免? 7. 谈谈你对AQS的理解,AQS如何实现可重入锁&…...

YARN运行流程
YARN是Hadoop资源管理器,他是一个通用资源管理平台和调度平台,可为上层应用提供统一的资源管理和调度,MapReduce等运算程序则相当于运行于操作系统上的应用程序,YARN为这些程序提供运算所需的资源内存、cpu。 YARN并不清楚用户提…...

java八股系列——SpringMVC从接受请求到完成响应的过程
Spring的MVC框架是围绕一个DispatcherServlet来设计的,这个Servlet会把请求分发给各个处理器,并支持可配置的处理器映射、视图渲染、本地化、时区与主题渲染等,甚至还能支持文件上传。 流程大致如下: 用户发起请求:用…...

Elasticsearch索引全生命周期
索引(Index)是Elasticsearch中最重要的概念之一,也是整个Elasticsearch操作的基础,它是相互关联的文档的一个集合。在Elasticsearch种,数据存储为 JSON 文档,每个文档将一组键(字段或属性的名称)与其对应的…...

汇编指令学习(LOOP)
一、xor异或操作,相同为0,不同为1xor eax,eaxeax异或eax,相同为0,并把结果存放到eax,简单说该语句就是想eax寄存器清零。二、ECX,计数器mov ecx,0x3将ecx寄存器设置为3三、DEC减一操作dec ecxecx寄存器的值…...

Linux 配置本地yum源
挂载光盘 进入包 配置路径,查看在线yum源 移动在线yum源到/home/目录下 进入vi,任意取名以.repo结尾即可 按住i进行编辑,输入以下内容 注意gpgcheck1是检验,配置本地yum源不需要检验 写入上图内容按住:输入wq,点击回车…...
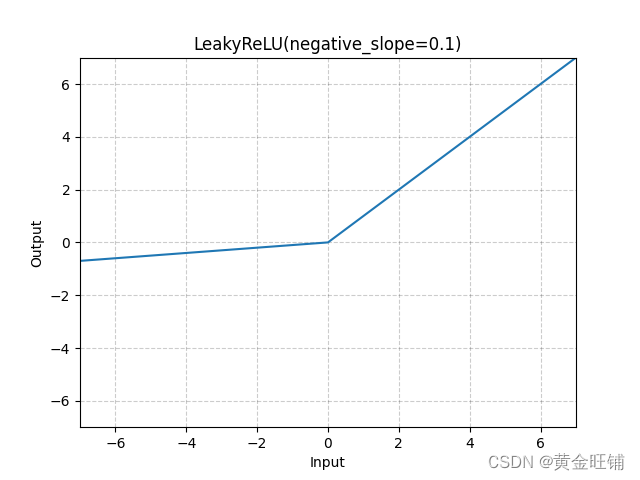
【PyTorch】教程:torch.nn.LeakyReLU
torch.nn.LeakyReLU 原型 CLASS torch.nn.LeakyReLU(negative_slope0.01, inplaceFalse) 参数 negative_slope (float) – 控制负值斜率,默认为 1e-2inplace (bool) – in-place 操作,默认为 False 定义 LeakyReLU(x)max(0,x)negative_slope∗min…...

【刷题】-- 基础 -- 二分查找
精于结构、敏于心智、熟于代码 方式:对于会的代码:学会以最快的速度构建,并以最快的速度书写;对于不会的代码:学会(以最短的路径下)看懂别人的代码。学会使用参考文档、熟悉每一个容器。 刷题位…...

Spark MLlib 特征工程
Spark MLlib 特征工程预处理特征选择归一化离散化Embedding向量计算特征工程制约了模型效果 : 决定了模型效果的上限 , 而模型调优只是在不停地逼近上限好的特征工程才能有好的模型 特征处理函数分类 : 预处理 : 将模型无法直接消费的数据,转为可消费的数据形式特…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
