LeetCode-Java:303、304区域检索(前缀和)
文章目录
- 题目
- 303、区域和检索(数组不可变)
- 304、二维区域和检索(矩阵不可变)
- 解
- ①303,一维前缀和
- ②304,二维前缀和
- 算法
- 前缀和
- 一维前缀和
- 二维前缀和
题目
303、区域和检索(数组不可变)
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
304、二维区域和检索(矩阵不可变)
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。
示例 1:

输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
解
①303,一维前缀和
class Solution {public int[] productExceptSelf(int[] nums) {int len=nums.length;int[] answer=new int[len];answer[0]=1;for(int i=1;i<len;i++){answer[i]=nums[i-1]*answer[i-1];}int R=nums[len-1]; // R存储右侧所有元素乘积for (int i = len - 2; i >= 0; i--) {answer[i] = answer[i] * R;R=R*nums[i];}return answer;}
}
②304,二维前缀和
class NumMatrix {int[][] sum;public NumMatrix(int[][] matrix) {int m=matrix.length,n=matrix[0].length;sum=new int[m+1][n+1];for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];}}}public int sumRegion(int row1, int col1, int row2, int col2) {return sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];}
}
算法
前缀和
前缀和是一种常见的算法技巧,用于快速计算数组中某个区间内元素的和,通常用于优化处理大量的区间求和问题,比如给定一个数组,询问其中某个连续区间内元素的和。
算法原理: 前缀和的核心思想是通过对数组进行预处理,计算出从数组开头到每个位置的元素累加和,然后利用这些预先计算好的累加和,在O(1)时间内求出任意区间的和。假设给定数组为A,其前缀和数组为prefix,其中prefix[i]表示数组A从0到i的元素和。
一维前缀和
假设给定数组为A = [1, 2, 3, 4, 5],其前缀和数组为prefix = [1, 3, 6, 10, 15]。
但在①②中,A数组的前缀和应当为prefix = [0,1, 3, 6, 10, 15],比原数组要多一个。
在计算任意区间的和时,通过在前缀和数组中添加0,可以统一处理起始位置为0的边界情况,无需单独考虑。例如,对于查询区间[0, 3],直接使用prefix[3]即可得到结果,无需特殊处理。
具体使用的时候建议用草稿纸绘制相关的数组或者矩阵的图形,进行检验。
二维前缀和
二维的前缀和更为复杂,
A = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
prefix = [ [1, 3, 6], [5, 12, 21], [12, 27, 45] ]
prefix[i] [j] = A[i] [j] + prefix[i-1] [j] + prefix[i] [j-1] - prefix[i-1] [j-1]
可以用下图帮助理解(图源LeetCode:负雪明烛):
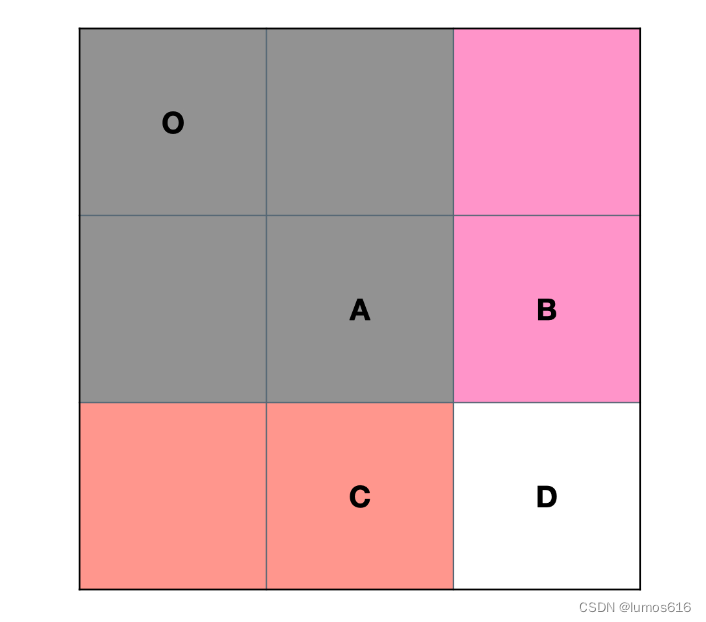
至于输出的公式,也类似于上面的用右下角位置加上左上角-1的位置减去区域右上角和左下角:
area=sum[row2+1] [col2+1]-sum[row1] [col2+1]-sum[row2+1] [col1]+sum[row1] [col1](为了方便书写代码,实际矩阵比原矩阵大一圈,所以这里所有的加减都在原矩阵基础上+1)
相关文章:

LeetCode-Java:303、304区域检索(前缀和)
文章目录 题目303、区域和检索(数组不可变)304、二维区域和检索(矩阵不可变) 解①303,一维前缀和②304,二维前缀和 算法前缀和一维前缀和二维前缀和 题目 303、区域和检索(数组不可变ÿ…...

出海业务的网络安全挑战
出海业务的扩展带来了巨大的市场机遇,同时也带来了不少网络安全挑战: 数据泄露与隐私保护:跨境数据传输增加了数据被截获和泄露的风险。地理位置限制和审查:某些地区的网络审查和地理位置限制可能阻碍企业正常开展业务。网络攻击…...

蓝桥杯考前准备— — c/c++
蓝桥杯考前准备— — c/c 对于输入输出函数 如果题目中有要求规定输入数据的格式与输出数据的格式,最好使用scanf()和prinrf()函数。 例如:输入的数据是 2020-02-18,则使用scanf("%d-%d-%d",&year,&mouth,&day)即可…...
【MATLAB源码-第4期】基于MATLAB的1024QAM误码率曲线,以及星座图展示。
1、算法描述 正交幅度调制(QAM,Quadrature Amplitude Modulation)是一种在两个正交载波上进行幅度调制的调制方式。这两个载波通常是相位差为90度(π/2)的正弦波,因此被称作正交载波。这种调制方式因此而得…...
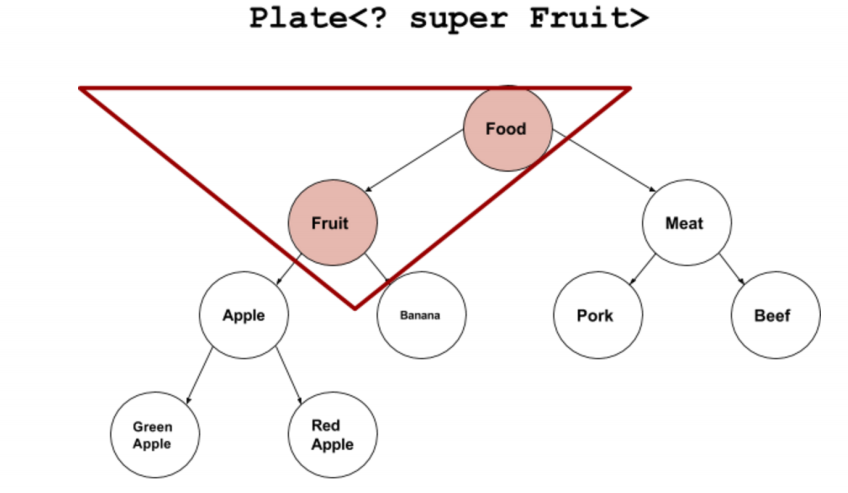
数据结构-----枚举、泛型进阶(通配符?)
文章目录 枚举1 背景及定义2 使用3 枚举优点缺点4 枚举和反射4.1 枚举是否可以通过反射,拿到实例对象呢? 5 总结 泛型进阶1 通配符 ?1.1 通配符解决什么问题1.2 通配符上界1.3 通配符下界 枚举 1 背景及定义 枚举是在JDK1.5以后引入的。主要用途是&am…...

线上问题监控 Sentry 接入全过程
背景: 线上偶发问题出现后 ,测试人员仅通过接口信息无法复现错误场景;并且线上环境的监控,对于提高系统的稳定性 (降低脱发率) 至关重要;现在线上监控工具这个多,为什么选择Sentry?…...
基础】以MySQL为例的数据库基础)
【数据库(MySQL)基础】以MySQL为例的数据库基础
文章目录 0. 本文用到的emp表,dept表,salgrade表1. MySQL入门2. 简单查询3. 字段计算4. 条件查询4.1 and4.2 null4.3 or4.4 and和or的优先级4.4 in 和 not in4.5 模糊查询 5. 排序5.1 简单排序5.2 两个字段排序5.3 综合排序 6. 一些常用函数6.1 大小写转换6.2 substr子字符串6.…...
权限修饰符,代码块,抽象类,接口.Java
1,权限修饰符 权限修饰符:用来控制一个成员能够被访问的范围可以修饰成员变量,方法,构造方法,内部类 👻👗👑权限修饰符的分类 🧣四种作用范围由小到大(private<空着…...

CSS设置文本
目录 概述: text-aling: text-decoration: text-transform: text-indent: line-height: letter-spacing: word-spacing: text-shadow: vertical-align: white-space: direction: 概述: 在CSS中我们可以设置文本的属性,就像Word文…...

【svg】—— java提取svg中的颜色
需要针对svg元素进行解析,并提取其中的颜色,首先需要知道svg中的颜色。针对svg中颜色的格式大致可以一般有纯色和渐变两种形式。对于渐变有分为:线性渐变和放射性渐变针对svg中的颜色支持16进制的格式,又可以支持RGB的格式&#x…...

论文分享 | FAST'23 阿里云提出的针对SMR优化的存储引擎SMRSTORE
今天分享的一篇最近阅读的论文是FAST23的SMRstore: A Storage Engine for Cloud Object Storage on HM-SMR Drives。 https://www.usenix.org/conference/fast23/presentation/zhou 这篇文章是由阿里巴巴公司完成的,在这篇文章中,团队针对SMR的特性提出了…...

题目:建造房屋 (蓝桥OJ3362)
问题描述: 代码: #include<bits/stdc.h> using namespace std; int n, m, k, ans, mod 1e9 7; long long dp[55][2605]; /*dp[i][j]:第i个街道上建j个房屋的总方案数枚举所有的转移,累加到dp[n][k]即总方案数 */ int main() {cin >> n &…...

智能合约平台开发指南
随着区块链技术的普及,智能合约平台已经成为了这个领域的一个重要趋势。智能合约可以自动化执行合同条款,大大减少了执行和监督合同条款所需的成本和时间。那么,如何开发一个智能合约平台呢?以下是一些关键步骤。 一、选择合适的区…...
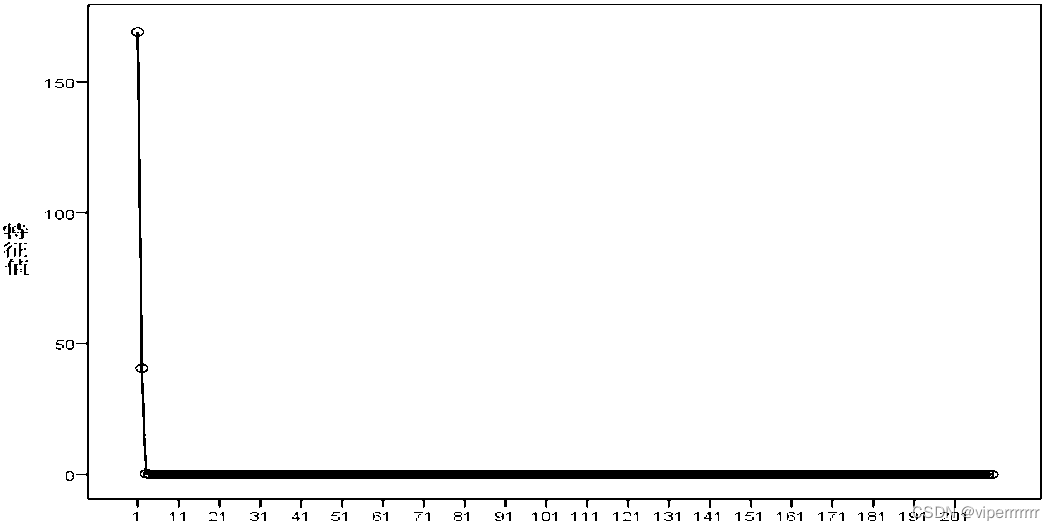
数学建模-最优包衣厚度终点判别法(主成分分析)
💞💞 前言 hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页ÿ…...

Mysql内存表及使用场景(12/16)
内存表(Memory引擎) InnoDB引擎使用B树作为主键索引,数据按照索引顺序存储,称为索引组织表(Index Organized Table)。 Memory引擎的数据和索引分开存储,数据以数组形式存放,主键索…...
Django交易商场
Hello,我是小恒不会java 最近学习django,写了一个demo,学到了不少东西。 我在GitHub上开源了,提示‘自行查看代码,维护,运行’。 最近有事,先发布代码了,我就随缘维护更新吧 介绍: 定…...

华为校园公开课走入上海交大,鸿蒙成为专业核心课程
4月12日,华为校园公开课在中国上海交通大学成功举办,吸引了来自计算机等相关专业的150余名学生参加。据了解,由吴帆、陈贵海、过敏意、吴晨涛、刘生钟等教授在中国上海交通大学面向计算机系本科生开设的《操作系统》课程,是该系学…...

【会员单位】泰州玉安环境工程有限公司
中华环保联合会理事单位 水环境治理专业委员会副主任委员单位 我会为会员单位提供服务: 1、企业宣传与技术项目对接; 2、企业标准、行业标准制定; 3、院士专家指导与人才培训 4、国际与国内会议交流 5、专精特新、小巨人等申报认证 6…...
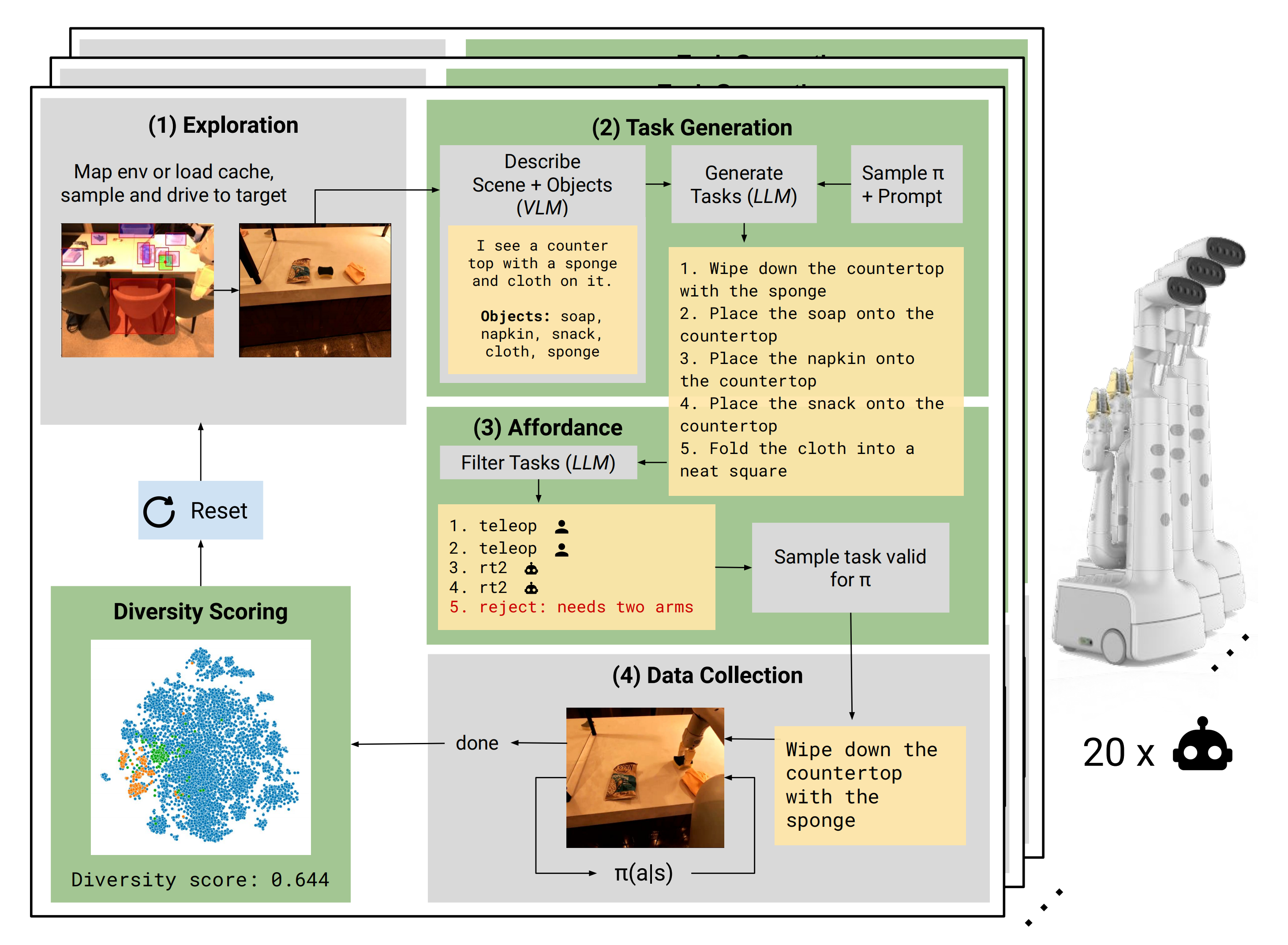
Google视觉机器人超级汇总:从RT、RT-2到AutoRT/SARA-RT/RT-Trajectory、RT-H
前言 随着对视觉语言机器人研究的深入,发现Google的工作很值得深挖,比如RT-2 想到很多工作都是站在Google的肩上做产品和应用,Google真是科技进步的核心推动力,做了大量大模型的基础设施,服(推荐重点关注下Googl…...
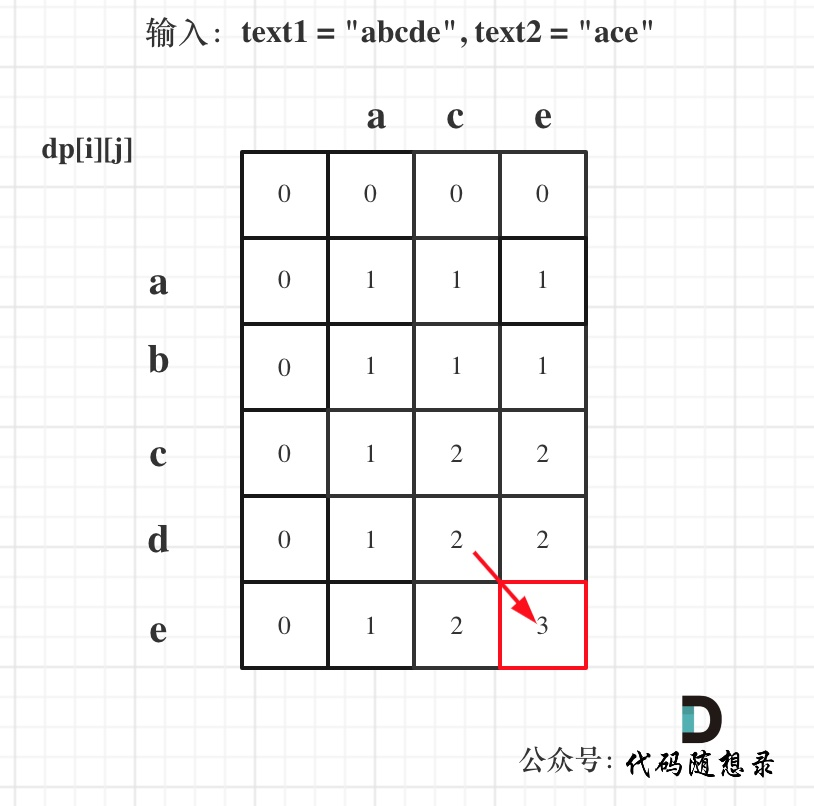
LeetCode-1143. 最长公共子序列【字符串 动态规划】
LeetCode-1143. 最长公共子序列【字符串 动态规划】 题目描述:解题思路一:动规五部曲解题思路二:1维DP解题思路三:0 题目描述: 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
