力扣207.课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]] 输出:false 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= 5000prerequisites[i].length == 20 <= ai, bi < numCoursesprerequisites[i]中的所有课程对 互不相同
这道题说人话就算判断这个有向图有没有环路。
我们知道拓扑排序可以用来判断是否有环路,不过仅仅是判断环路也可以直接用dfs,不需要完全写出拓扑排序,毕竟拓扑排序相比dfs还是更复杂一些。
下面给出上述两种思路的代码
1.拓扑排序判断
我的拓扑排序的代码思路是参考王道书介绍的思路
class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {vector<vector<int>> graph(numCourses, vector<int>(numCourses));//邻接矩阵vector<int> indegree(numCourses, 0);//每个节点的入度for (int i = 0; i < prerequisites.size(); i++) {graph[prerequisites[i][1]][prerequisites[i][0]] = 1;//构造邻接矩阵indegree[prerequisites[i][0]]++;//修改该点的入度}stack<int> stk;//用栈或队列都可以for (int i = 0; i < numCourses; i++) {if (indegree[i] == 0)//入度为0的点入栈stk.push(i);}int cnt = 0;//记录节点的数量while (!stk.empty()) {int i = stk.top();stk.pop();//如果是正常的拓扑排序,这里就可以输出节点了,本题只要求判断环路cnt++;//出栈的节点入度都为0,cnt++for (int j = 0; j < numCourses; j++) {//遍历当前节点的临边if (graph[i][j] != 0) {graph[i][j] = 0;//删除这条有向边indegree[j]--;//相邻边的入度减1if (indegree[j] == 0)//如果临边入度为0,入栈stk.push(j);}}}return cnt == numCourses;//最终的判断条件,cnt不为n,则有环路//因为有环路的情况下环路上的节点的入度不可能为0,就不会入栈,所以最后cnt的值不为n}
};下面用一张图作为示例:
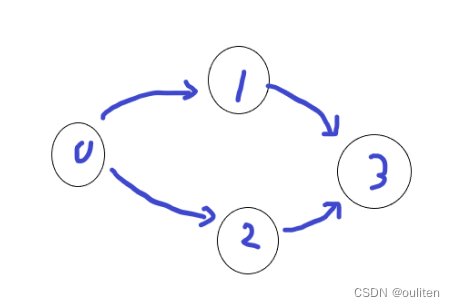
一开始只有0的度为0,所以0入栈,出栈时会执行这一段代码
for (int j = 0; j < numCourses; j++) {//遍历当前节点的临边if (graph[i][j] != 0) {graph[i][j] = 0;//删除这条有向边indegree[j]--;//相邻边的入度减1if (indegree[j] == 0)//如果临边入度为0,入栈stk.push(j);}}那么就把从0开始的弧都删掉,并把弧所指向的节点的入度减1
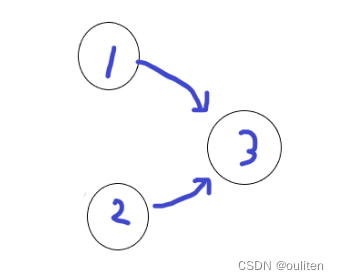
这时候1和2的入度就为0了,入栈。然后2先出栈,把2->3这段弧也删掉

但是此时3的入度不为0,也就先不会入栈。然后1出栈,把1->3这段弧删掉

这时候3的入度也为0,3入栈。3再出栈,3出栈反正啥也不会做。
最终,4个节点全部入了栈,因此cnt==n成立,该图是无环有向图。
如果是有环图,可以自己试一下,最后图里会剩下环,因为环上所有节点的入度都不为0,因此不会入栈。
2.dfs
class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {graph=vector<vector<int>>(numCourses, vector<int>(numCourses));//邻接矩阵vis = vector<int>(numCourses, 0);//visit数组valid = true;//标记是否存在环路vector<int> indegree(numCourses, 0);for (int i = 0; i < prerequisites.size(); i++) {graph[prerequisites[i][1]][prerequisites[i][0]] = 1;}//以上和拓扑排序都是一样的步骤for (int i = 0; i < numCourses; i++) {dfs(i);}return valid;}
private:void dfs(int u) {if (!valid) return;//如果存在环路直接返回if (vis[u] == 1) { valid = false; return; }//如果当前节点正在遍历,则表明存在环路if (vis[u] == 2) return;//如果当前节点已经遍历完成,直接返回vis[u] = 1;//vis置为1,表示当前节点正在dfs中for (int v = 0; v < vis.size(); v++) {//遍历当前节点的临边if (graph[u][v] != 0) {dfs(v);if (!valid) return;//有环直接退出}}vis[u] = 2;//置为2,表示当前节点已经走过了}bool valid;vector<int> vis;vector<vector<int>> graph;
};关键点在于vis数组的值有1和2的区分
画图解释,设1代表蓝色,2代表红色

从0出发,进行一次dfs,假设路径是0-1-3-4,那么最后1,3,4会变成红色,0还是蓝色

之后dfs会走2这条路

走到2后,会再次调用dfs(3),但是因为
if (vis[u] == 2) return;//如果当前节点已经遍历完成,直接返回所以valid还是true;
如果是有环路的情况,从0出发进行一次dfs
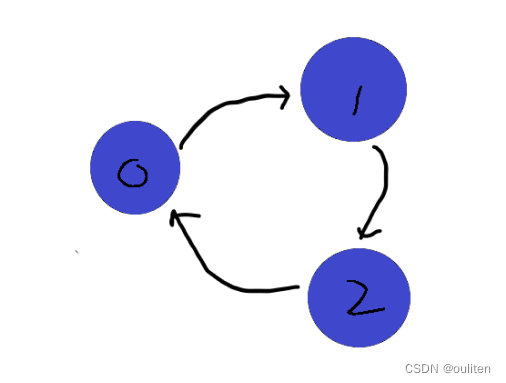
走到2后会再次调用dfs(0),而
if (vis[u] == 1) { valid = false; return; }//如果当前节点正在遍历,则表明存在环路所以有环路。
相关文章:

力扣207.课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 例如…...

十五届web模拟题整理
模拟赛一期 1.动态的Tab栏 请在 style.css 文件中补全代码。 当用户向下滚动的高度没有超过标题栏(即 .heading 元素)的高度时,保持 Tab 栏在其原有的位置。当滚动高度超过标题栏的高度时,固定显示 Tab 栏在网页顶部。 /* TODO…...

ubuntu20.04 安裝PX4 1.13
step1_install_depenences.sh #!/bin/bash #install gazebo 11 #install protobuf 3.19.6python3 -m pip install --upgrade pip python3 -m pip install --upgrade Pillow# 將 empy 的版本調整爲3.3.4 pip3 uninstall empy pip3 install empy3.3.4sudo apt-get update sudo ap…...
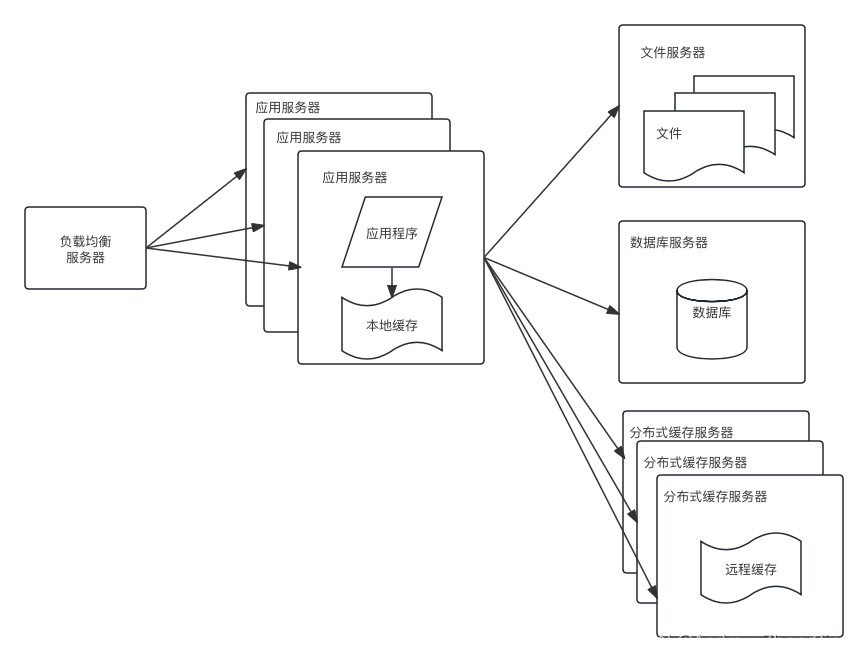
大型网站系统架构演化
大型网站质量属性优先级:高性能 高可用 可维护 应变 安全 一、单体架构 应用程序,数据库,文件等所有资源都在一台服务器上。 二、垂直架构 应用和数据分离,使用三台服务器:应用服务器、文件服务器、数据服务器 应用服…...
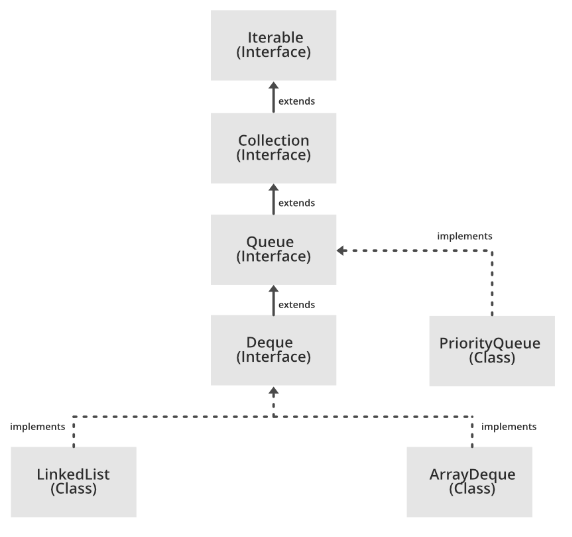
探索Java中的栈:Stack与Deque(ArrayDeque和LinkedList)
文章目录 1. 栈(Stack)1.1 定义方式1.2 特点1.3 栈的层次结构 2. 双端队列(Deque)2.1 定义方式及继承关系2.2 特点:2.3 ArrayDeque2.4 LinkedList2.5 Deque 的各种方法2.6 如何选择ArrayDeque和LinkedList 3. 如何选择…...

实践笔记-03 docker buildx 使用
docker buildx 使用 1.启用docker buildx2.启用 binfmt_misc3.从默认的构建器切换到多平台构建器3.1创建buildkitd.toml文件(私有仓库是http没有证书的情况下,需要配置)3.2创建构建器并使用新创建的构建器 4.构建多架构镜像并推送至harbor仓库…...

【数据结构与算法】之8道顺序表与链表典型编程题心决!
个人主页:秋风起,再归来~ 数据结构与算法 个人格言:悟已往之不谏,知来者犹可追 克心守己,律己则安! 目录 1、顺序表 1.1 合并两个有序数组 1.2 原地移除数组中所有的元素va…...

Go 源码之旅-开篇
欢迎来到《Go 源码之旅》专栏!在这个专栏中,我们将深入探索 Go 编程语言的内部数据结构的工作原理,一起踏上一段令人兴奋的源码之旅。 我们将一步步解析关键的数据结构底层工作原理以及一些常用框架的设计原理及其源码。 无论你是初学者还是…...

spring的事件推送
本质上是设计模式中的观察者模式。 一、什么是观察者模式 观察者模式是一种行为型设计模式,它定义了一种一对多的依赖关系,当一个对象的状态发生改变时,其所有依赖者都会收到通知并自动更新。 二、什么是spring的事件推送 在 Spring 的事…...

计算机网络—HTTPS协议详解:工作原理、安全性及应用实践
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:ヒューマノイド—ずっと真夜中でいいのに。 1:03━━━━━━️💟──────── 5:06 🔄 ◀️ ⏸…...

卫星遥感影像在农业方面的应用及评价
一、引言 随着科技的进步,卫星遥感技术在农业领域的应用越来越广泛。卫星遥感技术以其宏观、快速、准确的特点,为农业生产和管理提供了有力的技术支撑。本文将对卫星遥感在农业方面的应用进行详细介绍,并通过具体案例进行说明。 二、…...
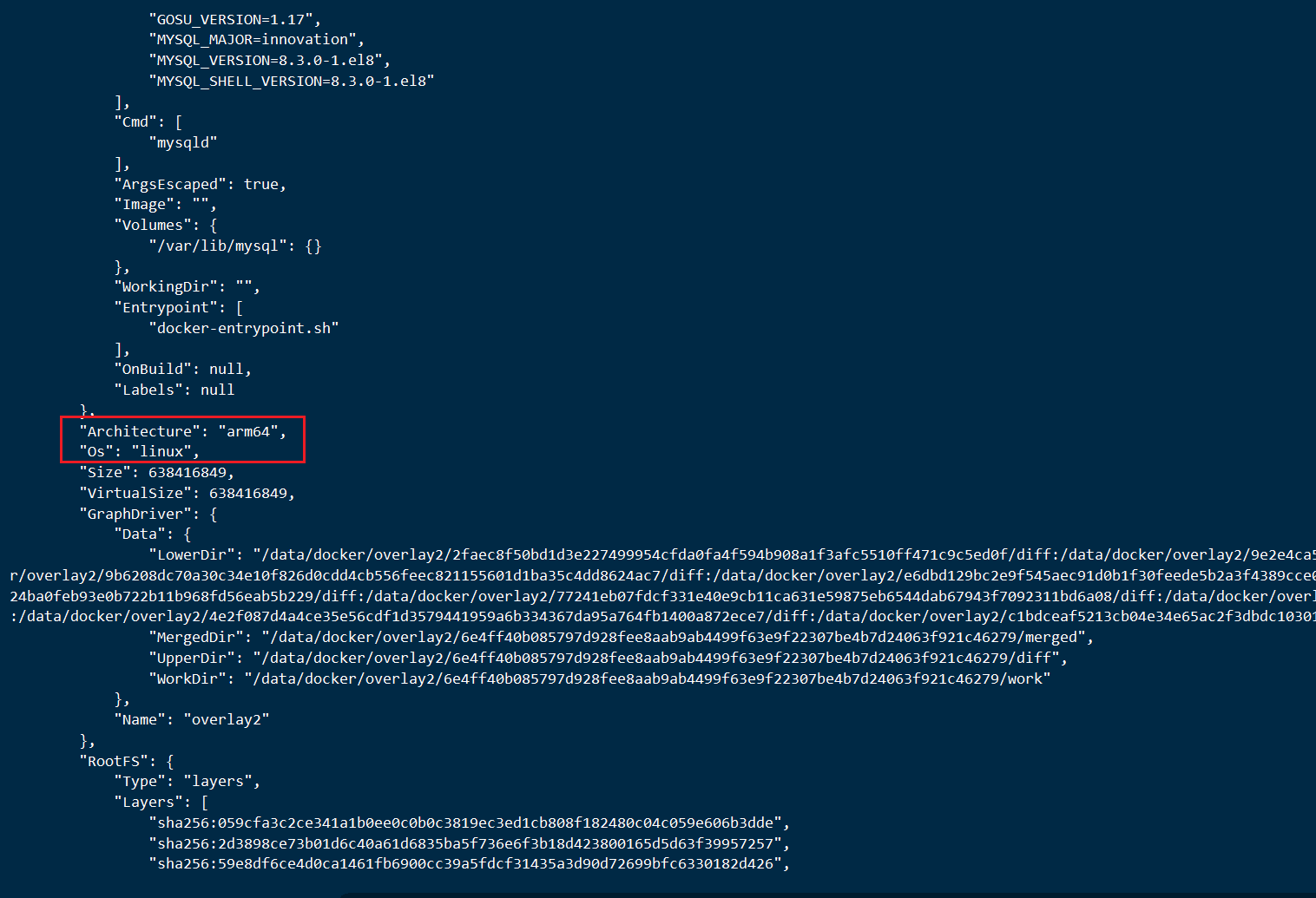
docker pull镜像的时候指定arm平台
指定arm平台 x86平台下载arm平台的镜像包 以mysql镜像为例 docker pull --platform linux/arm64 mysqldocker images查看镜像信息 要查看Docker镜像的信息,可以使用docker inspect命令。这个命令会返回镜像的详细信息,包括其元数据和配置。 docker i…...

如何通过OceanBase V4.2 动态采样优化查询性能
OceanBase v4.2 推出了优化器动态采样的功能,在SQL运行过程中,该功能会收集需要的统计信息,协助优化器制定出更好的执行计划,进一步提升了查询性能。 影响查询性能的因素是什么?为何你的优化器效果不佳? …...
Vue3---基础1(认识,创建)
变化 相对于Vue2,Vue3的变化: 性能的提升 打包大小减少 41% 初次渲染快 55%,更新渲染快133% 内存减少54% 源码的升级 使用 proxy 代替 defineProperty 实现响应式 重写虚拟 DOM 的实现和 Tree-shaking TypeScript Vue3就可以更好的支持TypeSc…...

JAVA集合ArrayList
目录 ArrayList概述 add(element) 用法 add(index, element)用法 remove(element)用法 remove(index)用法 get(index)用法 set(index,element) 练习 test1 定义一个集合,添加字符串,并进行遍历&…...

Bitmap OOM
老机器Bitmap预读仍然OOM,无奈增加一段,终于不崩溃了。 if (Build.VERSION.SDK_INT < 21)size 2; 完整代码: Bitmap bitmap; try {//Log.e(Thread.currentThread().getStackTrace()[2] "", surl);URL url new URL(surl);…...

基于深度学习的人脸表情识别系统(PyQT+代码+训练数据集)
基于深度学习的人脸表情识别系统(PyQT代码训练数据集) 前言一、数据集1.1 数据集介绍1.2 数据预处理 二、模型搭建三、训练与测试3.1 模型训练3.2 模型测试 四、PyQt界面实现 前言 本项目是基于mini_Xception深度学习网络模型的人脸表情识别系统&#x…...

Qt 中的项目文件解析和命名规范
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、Qt项目文件解析 1、.pro 文件解析 2、widget.h 文件解析 3、main.cpp 文件解析 4、widget.cpp…...

【chatGPT】我:在Cadence Genus软件中,出现如下问题:......【4】
我 在Cadence Genus中,tcl代码为:foreach clk $clk_list{ set clkName [lindex $clk_list 0] set targetFreq [lindex $clk_list 1] set uncSynth [lindex $clk_list 4] set clkPeriod [lindex “%.3f” [expr 1 / $targetFreq]] … } 以上代码出现如下…...
在JAVA中的应用)
单例模式(Singleton Pattern)在JAVA中的应用
在软件开发中,设计模式是解决特定问题的一种模板或者指南。它们是在多年的软件开发实践中总结出的有效方法。JAVA设计模式广泛应用于各种编程场景中,以提高代码的可读性、可维护性和扩展性。本文将介绍单例模式,这是一种常用的创建型设计模式…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
