docker、ctr、crictl命令对比
| 命令 | docker | ctr(containerd) | crictl(kubernetes) |
|---|---|---|---|
| 查看运行的容器 | docker ps | ctr task ls/ctr container ls | crictl ps |
| 查看镜像 | docker images | ctr image ls | crictl images |
| 查看容器日志 | docker logs | 无 | crictl logs |
| 查看容器数据信息 | docker inspect | ctr container info | crictl inspect |
| 查看容器资源 | docker stats | 无 | crictl stats |
| 启动/关闭已有的容器 | docker start/stop | ctr task start/kill | crictl start/stop |
| 运行一个新的容器 | docker run | ctr run | 无(最小单元为pod) |
| 修改镜像标签 | docker tag | ctr image tag | 无 |
| 创建一个新的容器 | docker create | ctr container create | crictl create |
| 导入镜像 | docker load | ctr image import | 无 |
| 导出镜像 | docker save | ctr image export | 无 |
| 删除容器 | docker rm | ctr container rm | crictl rm |
| 删除镜像 | docker rmi | ctr image rm | crictl rmi |
| 拉取镜像 | docker pull | ctr image pull | ctictl pull |
| 推送镜像 | docker push | ctr image push | 无 |
| 在容器内部执行命令 | docker exec | 无 | crictl exec |
相关文章:

docker、ctr、crictl命令对比
命令dockerctr(containerd)crictl(kubernetes)查看运行的容器docker psctr task ls/ctr container lscrictl ps查看镜像docker imagesctr image lscrictl images查看容器日志docker logs无crictl logs查看容器数据信息docker insp…...
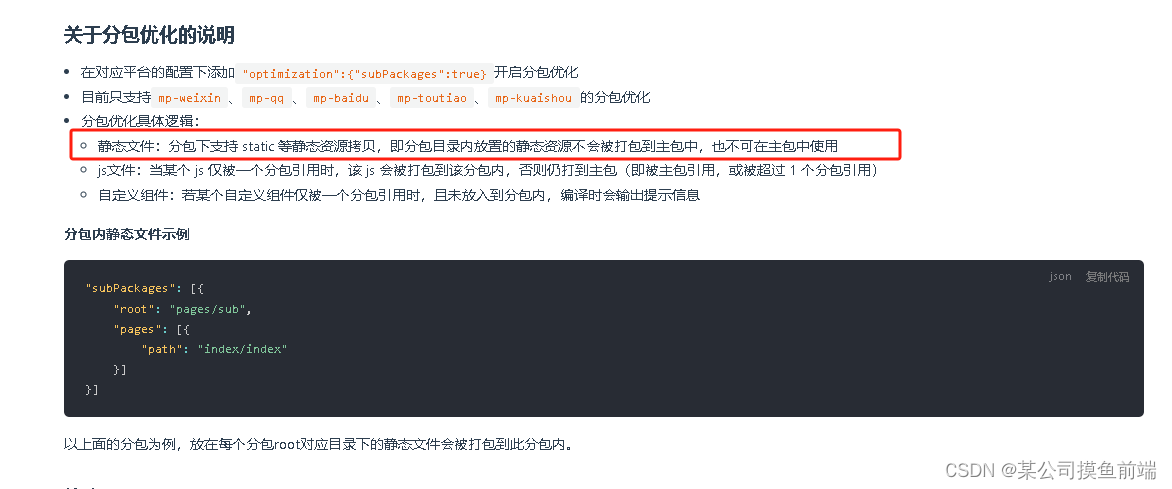
uniapp 编译后分包下静态图片404问题解决方案
如上图官方说明: 在分包下建立一个static文件夹即可: 分包内代码引用图片 <image src"/分包名称/img/图片名称"></image> <image src"/dataView/img/图片名称"></image>...

第十二届蓝桥杯大赛软件赛省赛Java 大学 B 组题解
1、ASC public class Main {public static void main(String[] args) {System.out.println(...

关于openai和chatgpt、gpt-4、PyTorch、TensorFlow 两者和Transformers的关系
近两年,随着人工智能的火爆,不论通过哪个渠道,相信我们都听说过openai、gpt等这类名词,那么它们到底是什么意思,请看下文。 openai:是一家人工智能公司; openai-api:是openai提供的api…...

C 共用体
共用体是一种特殊的数据类型,允许您在相同的内存位置存储不同的数据类型。您可以定义一个带有多成员的共用体,但是任何时候只能有一个成员带有值。共用体提供了一种使用相同的内存位置的有效方式。 定义共用体 为了定义共用体,您必须使用 u…...

智能合约:未来数字经济的基石
智能合约是一种自动执行交易的计算机协议,它以代码形式规定了交易双方的权利和义务,具有高度的可靠性和安全性。随着数字经济的发展,智能合约的重要性日益凸显,将成为未来数字经济的基石。 首先,智能合约在金融领域的应…...

第十一届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组
第十一届蓝桥杯大赛软件赛省赛C/C 大学 B 组 文章目录 第十一届蓝桥杯大赛软件赛省赛C/C 大学 B 组1、字串排序2、门牌制作3、既约分数4、蛇形填数5、跑步锻炼6、七段码7、成绩统计8、回文日期9、子串分值和10、平面切分 1、字串排序 // 转载博客链接 https://blog.csdn.net/we…...
——元表与元方法)
Lua语法(三)——元表与元方法
参考链接: 系列链接: Lua语法(一) 系列链接: Lua语法(二)——闭包/日期和时间 系列链接: Lua语法(三)——元表与元方法 系列链接: Lua语法(四)——协程 系列链接: Lua语法(五)——垃圾回收 系列链接: Lua语法(六)——面相对象编程 元表与元方法目录 简介正文元表元方法表相关常…...
——垃圾回收)
Lua语法(五)——垃圾回收
参考链接: 系列链接: Lua语法(一) 系列链接: Lua语法(二)——闭包/日期和时间 系列链接: Lua语法(三)——元表与元方法 系列链接: Lua语法(四)——协程 系列链接: Lua语法(五)——垃圾回收 系列链接: Lua语法(六)——面相对象编程 Lua语法 五——垃圾回收 垃圾回收弱引用表__m…...

已解决java.net.NoRouteToHostException: 无法到达主机异常的正确解决方法,亲测有效!!!
已解决java.net.NoRouteToHostException: 无法到达主机异常的正确解决方法,亲测有效!!! 目录 问题分析 报错原因 解决思路 解决方法 检查网络连接 核实目标地址 检查防火墙和路由器规则 验证VPN/代理设置 修正网络配置 …...

代码随想录算法训练营第三十八天| 509. 斐波那契数,70. 爬楼梯,746. 使用最小花费爬楼梯
题目与题解 参考资料:动态规划基础 动态规划五步曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 题目链接:509. 斐波那契数 代码随想录题解&am…...
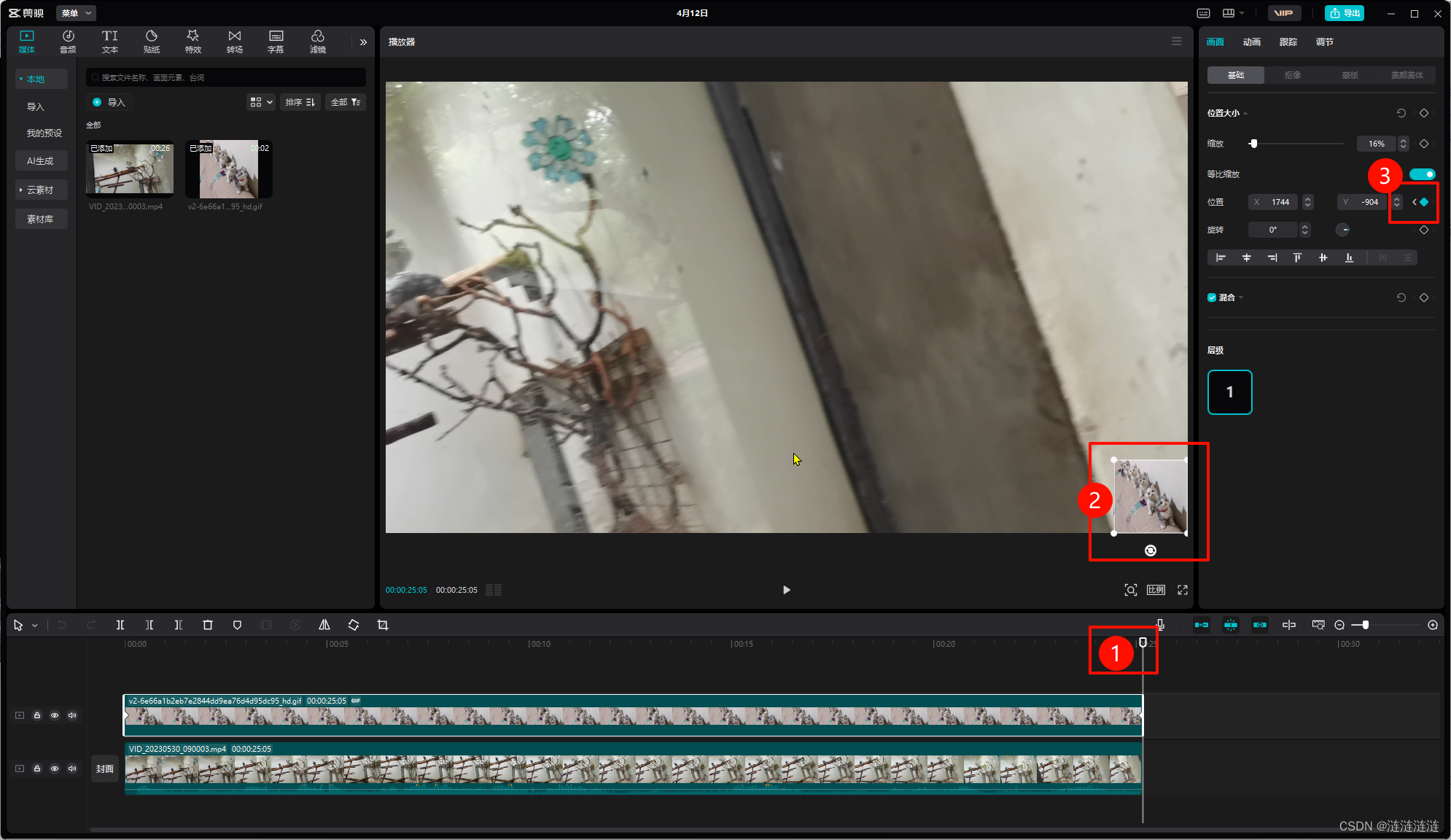
视频中会动的进度条
视频中会动的进度条 1.成果展示:2.步骤: 1.成果展示: 2.步骤:...
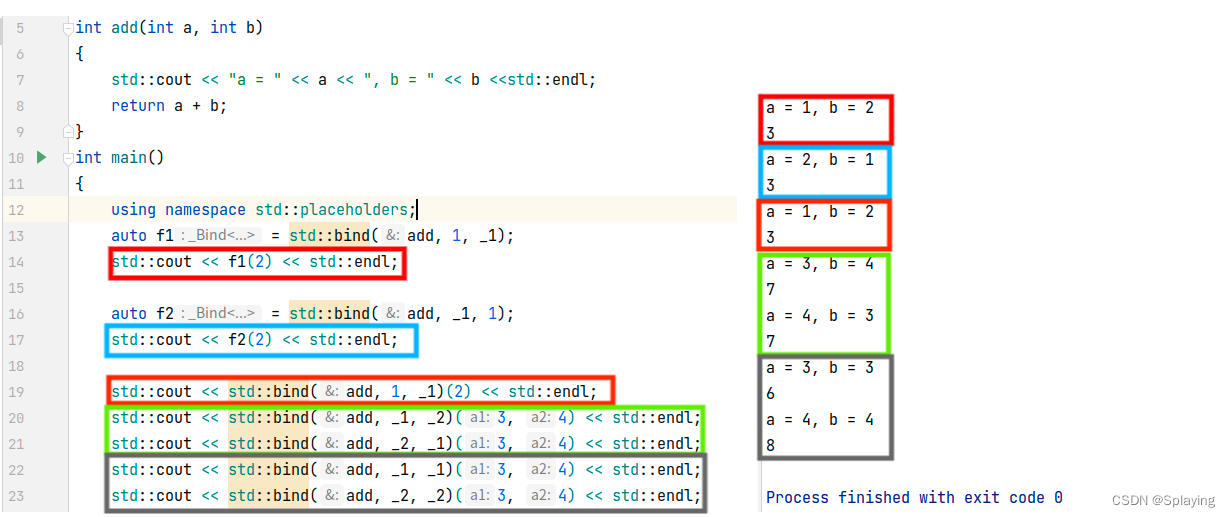
C++高级特性:柯里化过程与std::bind(六)
1、柯里化过程 1.1、operator()的引入 现在需要完成这样一个需求:有一个函数每次调用返回的结果不一样。例如:两次调用的返回值都不一样那么就可以达到这种目的 1.1.1、简单点的写法 可以给一个全局的变量(静态变量)ÿ…...
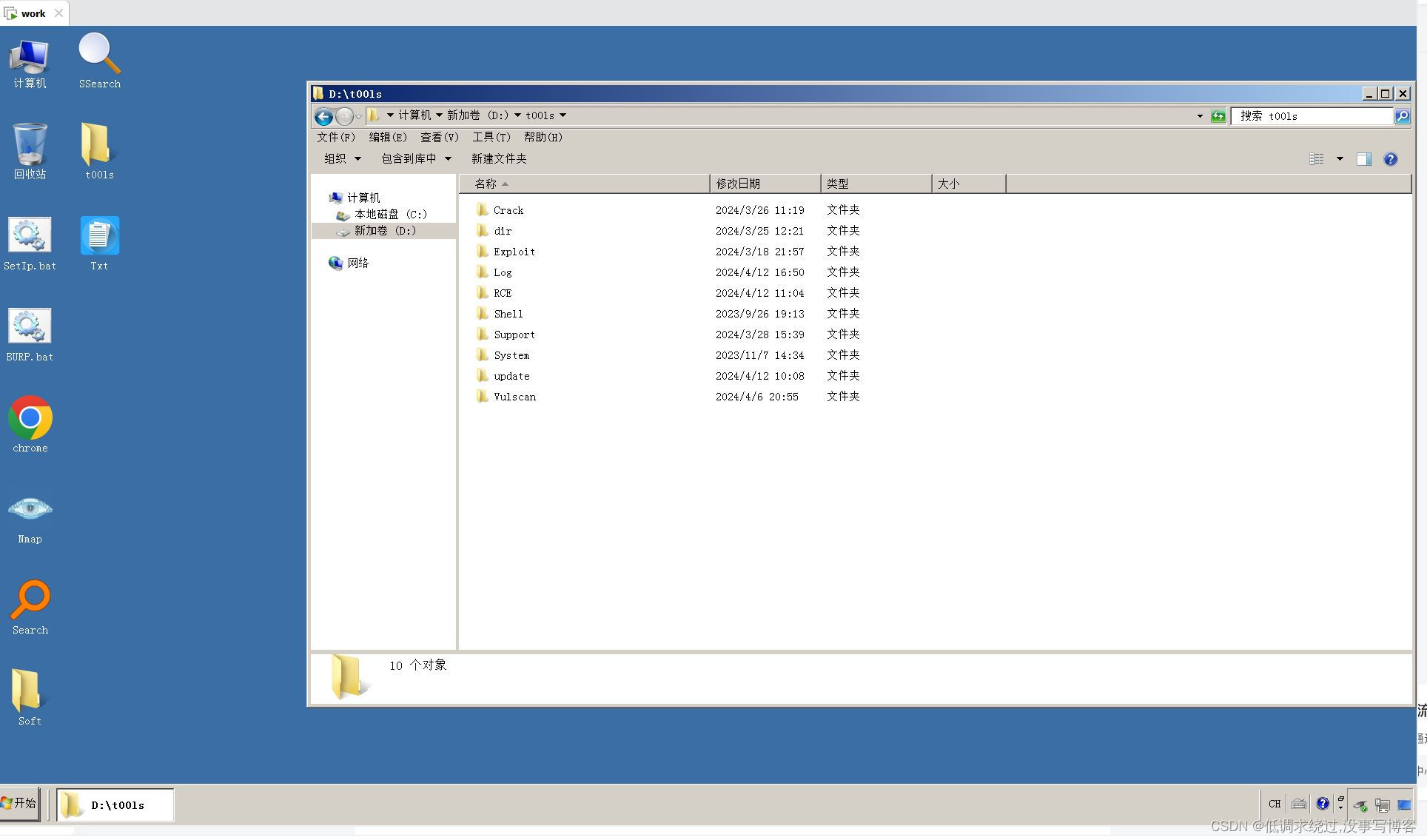
vmware虚拟机补救
更新了虚拟机里面工具和资料,进行了磁盘整理和压缩,虚拟机运行进不去系统了。 网站找的修复方法均不可行。补救措施:利用DiskGenius.exe(要用高版本不然复制的时候就知道了) DG1342.rar - 蓝奏云 加载虚拟硬盘 2008x…...

数据结构(算法)
总结,建议看EXCEL的《算法》页签,不然感觉有点乱 备注原理/步骤时间复杂度空间复杂度串的应用模式匹配简单/暴力O(mn) KMP O(mn) 树的应用树哈夫曼树1、带权路径长度WPL 2、外部排序-最佳归并树1、哈夫曼树的度,只有0和m(m叉…...
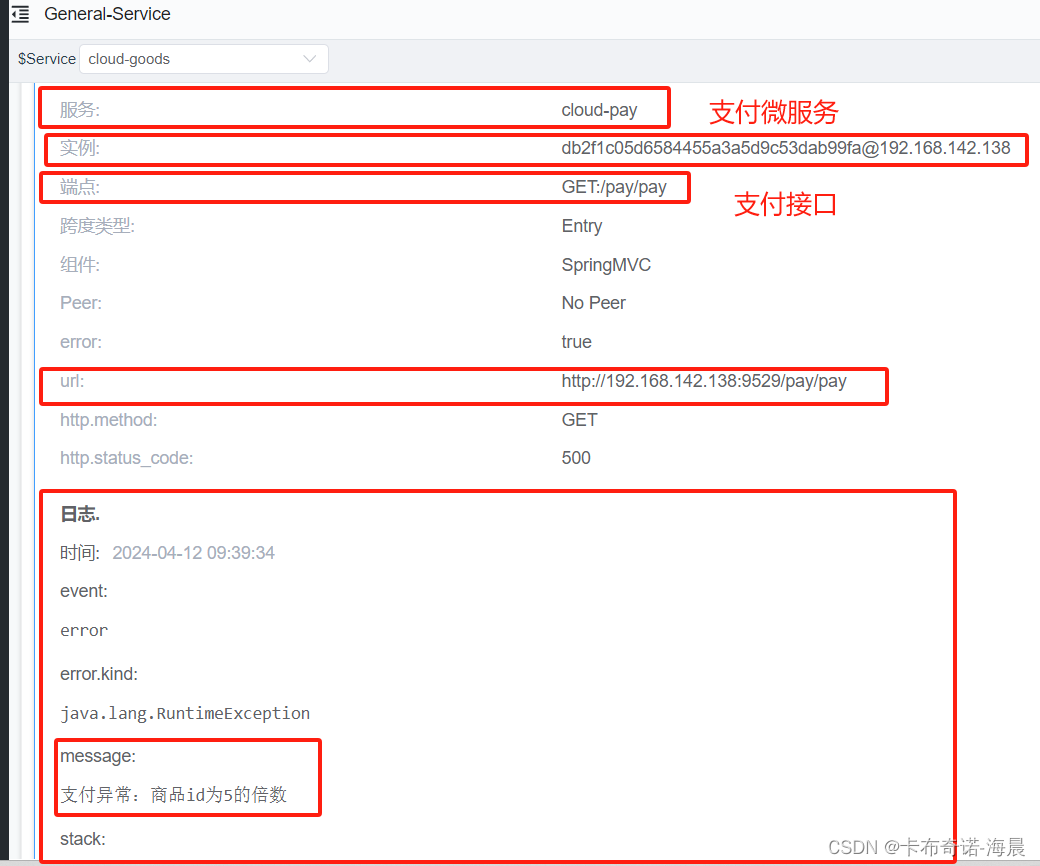
SpringCloud集成SkyWalking链路追踪并收集日志2
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录 数学质因数分解辗转相除法求最大公约数最小公倍数:快速幂乘法逆元费马小定理 逆元乘法逆元素数判定与埃式筛法朴素素数判定法埃式筛法 图论并查集T3:真题--合根植物DijkstraFloyd 基础算法递归,循环,前缀和,差分STL 数学…...

python 最简单的网页爬虫
import requests url"https://news.ifeng.com/c/8OZc7eV01sM" rrequests.get(url) print(r.status_code) print(r.iter_lines()) # 获取响应的内容 content r.text# 打印网页内容 print(content) # responser.json() # print(response) 爬虫知识讲解: …...

二叉树-数据结构
二叉树-数据结构 二叉树是属性结构的一个重要类型。 如下图二叉树形状 二叉树特征如下: 1.二叉树由 n(n > 0) 个节点组成 2.如果 n 为 0,则为空树 3.如果 n 1,则只有一个节点称为根节点(root) 4.每个节点最多有两个节点,节…...

ansible使用shell模块的环境变量问题
在本机写了一个shell脚本,关于操作mysql的,在本机执行脚本可以正常操作数据库,脚本运行正常。 但是使用ansible ansible -i ./hosts test_teledb -m copy -a "src/etc/ansible/scripts/check.sh dest/tmp"ansible -i ./hosts test…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
