Jones矩阵符号运算
文章目录
- Jones向量
- Jones矩阵
有关Jones矩阵、Jones向量的基本原理,可参考这个: 通过Python理解Jones矩阵,本文主要介绍sympy中提供的有关偏振光学的符号计算工具
Jones向量
Jones向量是描述光线偏振状态的重要工具,例如一个偏振角度为 ψ \psi ψ的Jones向量可表示为
J ^ = [ cos ψ sin ψ ] \hat J=\begin{bmatrix} \cos\psi\\ \sin\psi \end{bmatrix} J^=[cosψsinψ]
【jones_vector】是sympy.physics.optics.polarization中用于表示Jones向量的对象,其调用方法为
jones_vector(psi, chi)
其中,psi为 x x x方向的极化角度;chi为与晶体主轴的夹角。
import sympy
from sympy.physics.optics.polarization import jones_vector
psi = sympy.symbols('psi')
V = jones_vector(psi, 0)
sympy.pprint(V)
'''
⎡cos(ψ)⎤
⎢ ⎥
⎣sin(ψ)⎦
'''
Jones矩阵
Jones矩阵可以描述Jones向量在通过偏振元件后的变化,例如偏振光在经过 x x x线偏振片之后, sin ψ \sin\psi sinψ会被滤掉,从而其对应的Jones矩阵可表示为
[ 1 0 0 0 ] \begin{bmatrix} 1&0\\0&0 \end{bmatrix} [1000]
sympy.physics.optics.polarization中封装了多种偏振器件的Jones矩阵。
linear_polarizer(theta=0)线偏振光half_wave_retarder(theta)半波片quarter_wave_retarder(theta)λ / 4 \lambda/4 λ/4波片phase_retarder(theta=0, delta=0)相位延迟reflective_filter(R)反射滤光片,R为反射率transmissive_filter(T)透射滤光片,T为透过率polarizing_beam_splitter(Tp=1, Rs=1, Ts=0, Rp=0, phia=0, phib=0)偏振片
import sympy
from sympy.physics.optics.polarization import half_wave_retarder
theta = sympy.symbols("theta", real=True)
HWP = half_wave_retarder(theta)
sympy.latex(HWP)
结果如下
[ − i ( − sin 2 θ + cos 2 θ ) − 2 i sin θ cos θ − 2 i sin θ cos θ − i ( sin 2 θ − cos 2 θ ) ] \left[\begin{matrix}- i \left(- \sin^{2}\theta + \cos^{2}{\theta}\right) & - 2 i \sin\theta \cos\theta\\- 2 i \sin\theta\cos\theta & - i \left(\sin^{2}\theta - \cos^{2}\theta\right)\end{matrix}\right] [−i(−sin2θ+cos2θ)−2isinθcosθ−2isinθcosθ−i(sin2θ−cos2θ)]
偏振片的参数较多,现列如下polarizing_beam_splitter(Tp=1, Rs=1, Ts=0, Rp=0, phia=0, phib=0)
- J 琼斯矩阵
- Tp p偏振光的透过率
- Rs s偏振光的反射率
- Ts s偏振光的透过率
- Rp p偏振光的反射率
- phia 透射和反射分量的相位差
- phib 透射和反射分量的相位差
相关文章:

Jones矩阵符号运算
文章目录 Jones向量Jones矩阵 有关Jones矩阵、Jones向量的基本原理,可参考这个: 通过Python理解Jones矩阵,本文主要介绍sympy中提供的有关偏振光学的符号计算工具 Jones向量 Jones向量是描述光线偏振状态的重要工具,例如一个偏振…...

解决 App 自动化测试的常见痛点!
App 自动化测试中有些常见痛点问题,如果框架不能很好的处理,就可能出现元素定位超时找不到的情况,自动化也就被打断终止了。很容易打消做自动化的热情,导致从入门到放弃。比如下面的两个问题: 一是 App 启动加载时间较…...

2016NOIP普及组真题 1. 买铅笔
线上OJ: 一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid1973 核心思想: 向上取整的代码 (m (n-1))/n 。(本题考点与2023年J组的第一和第二题一样) 比如需要买31支笔,每包30支,则需要…...
机器学习—数据集(二)
1可用数据集 公司内部 eg:百度 数据接口 花钱 数据集 学习阶段可用的数据集: sklearn:数据量小,方便学习kaggle:80万科学数据,真实数据,数据量大UCI:收录了360个数据集,覆盖科学、生活、经济等…...

华为S5735S核心交换配置实例
以下脚本实现创建vlan2,3,IP划分,DHCP启用,接口划分,ssh,telnet,http,远程登录启用 默认用户创建admin/admin123提示首次登录需要更改用户密码S5735产品手册更多功能配置,移步官网参考手册配置 system-viewsysname t…...

Mysql主从复制安装配置
mysql主从复制安装配置 1、基础设置准备 #操作系统: centos6.5 #mysql版本: 5.7 #两台虚拟机: node1:192.168.85.111(主) node2:192.168.85.112(从)2、安装mysql数据库 #详细安装和卸载的步骤…...

【刷题】图论——最小生成树:Prim、Kruskal【模板】
假设有n个点m条边。 Prim适用于邻接矩阵存的稠密图,时间复杂度是 O ( n 2 ) O(n^2) O(n2),可用堆优化成 O ( n l o g n ) O(nlogn) O(nlogn)。 Kruskal适用于稀疏图,n个点m条边,时间复杂度是 m l o g ( m ) mlog(m) mlog(m)。 Pr…...

使用uniapp实现小程序获取wifi并连接
Wi-Fi功能模块 App平台由 uni ext api 实现,需下载插件:uni-WiFi 链接:https://ext.dcloud.net.cn/plugin?id10337 uni ext api 需 HBuilderX 3.6.8 iOS平台获取Wi-Fi信息需要开启“Access WiFi information”能力登录苹果开发者网站&…...

回忆杀之手搓当年搓过的Transformer
整体代码 import mathimport paddle import paddle.nn as nn import paddle.nn.functional as Fclass MaskMultiHeadAttention(nn.Layer):def __init__(self, hidden_size, num_heads):super(MaskMultiHeadAttention, self).__init__()assert hidden_size % num_heads 0, &qu…...

【AR】使用深度API实现虚实遮挡
遮挡效果 本段描述摘自 https://developers.google.cn/ar/develop/depth 遮挡是深度API的应用之一。 遮挡(即准确渲染虚拟物体在现实物体后面)对于沉浸式 AR 体验至关重要。 参考下图,假设场景中有一个Andy,用户可能需要放置在包含…...

python-pytorch实现skip-gram 0.5.001
python-pytorch实现skip-gram 0.5.000 数据加载、切词准备训练数据准备模型和参数训练保存模型加载模型简单预测获取词向量画一个词向量的分布图使用词向量计算相似度参考数据加载、切词 按照链接https://blog.csdn.net/m0_60688978/article/details/137538274操作后,可以获得…...

C语言:约瑟夫环问题详解
前言 哈喽,宝子们!本期为大家带来一道C语言循环链表的经典算法题(约瑟夫环)。 目录 1.什么是约瑟夫环2.解决方案思路3.创建链表头结点4.创建循环链表5.删除链表6.完整代码实现 1.什么是约瑟夫环 据说著名历史学家Josephus有过以下…...
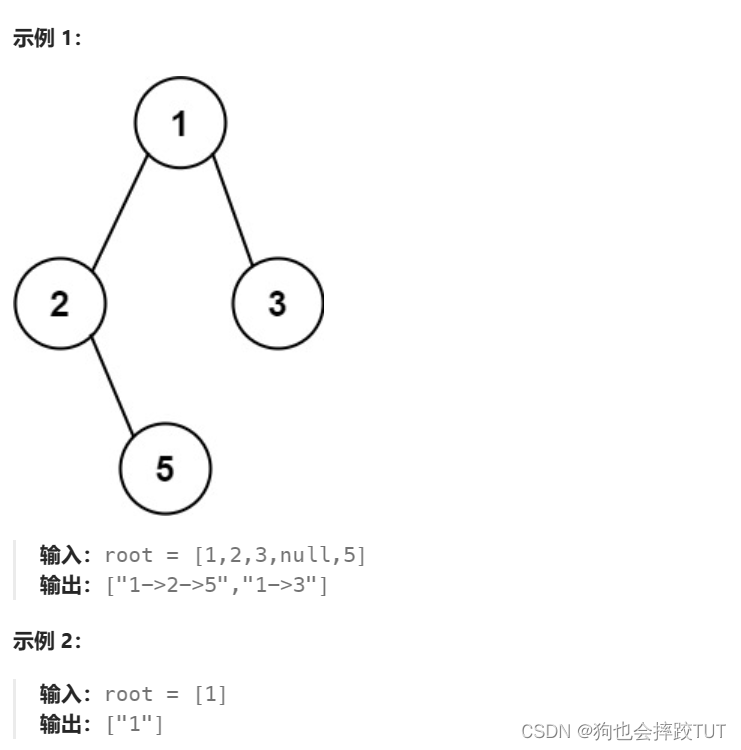
【刷题篇】回溯算法(二)
文章目录 1、求根节点到叶节点数字之和2、二叉树剪枝3、验证二叉搜索树4、二叉搜索树中第K小的元素5、二叉树的所有路径 1、求根节点到叶节点数字之和 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...
Windows系统本地部署Jupyter Notebook并实现公网访问编辑笔记
文章目录 1.前言2.Jupyter Notebook的安装2.1 Jupyter Notebook下载安装2.2 Jupyter Notebook的配置2.3 Cpolar下载安装 3.Cpolar端口设置3.1 Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 在数据分析工作中,使用最多的无疑就是各种函数、图表、…...
Ansible 实战Shell 插件和模块工具)
自动化运维(二十七)Ansible 实战Shell 插件和模块工具
Ansible 支持多种类型的插件,这些插件可以帮助你扩展和定制 Ansible 的功能。每种插件类型都有其特定的用途和应用场景。今天我们一起学习Shell 插件和模块工具。 一、 Shell 插件 Ansible shell 插件决定了 Ansible 如何在远程系统上执行命令。这些插件非常关键&a…...

Jenkins使用-绑定域控与用户授权
一、Jenkins安装完成后,企业中使用,首先需要绑定域控以方便管理。 操作方法: 1、备份配置文件,防止域控绑定错误或授权策略选择不对,造成没办法登录,或登录后没有权限操作。 [roottest jenkins]# mkdir ba…...
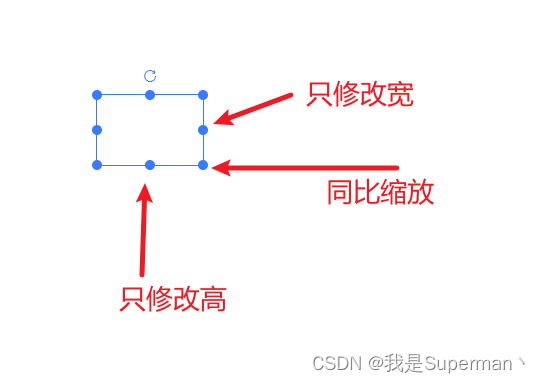
【前端】es-drager 图片同比缩放 缩放比 只修改宽 只修改高
【前端】es-drager 图片同比缩放 缩放比 ES Drager 拖拽组件 (vangleer.github.io) 核心代码 //初始宽 let width ref(108)//初始高 let height ref(72)//以下两个变量 用来区分是单独的修改宽 还是高 或者是同比 //缩放开始时的宽 let oldWidth 0 //缩放开始时的高 let o…...

蓝桥杯第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 A 组题解
1.幸运数 题目链接:0幸运数 - 蓝桥云课 (lanqiao.cn) #include<bits/stdc.h> using namespace std; bool deng(string& num){int n num.size();int qian 0,hou 0;for(int i0;i<n/2;i) qian (num[i]-0);for(int in/2;i<n;i) hou (num[i]-0);r…...
eclipse .project
.project <?xml version"1.0" encoding"UTF-8"?> <projectDescription> <name>scrm-web</name> <comment></comment> <projects> </projects> <buildSpec> <buil…...

react的闭包陷阱
React 的闭包陷阱是指在使用 React Hooks 时,由于闭包特性导致在某些函数或异步操作中无法正确访问到更新后状态或 prop 的值,而仍旧使用了旧值。下面通过几个代码示例来具体说明闭包陷阱的几种常见情形: 示例 1: useState 闭包陷阱 import…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
