【刷题篇】回溯算法(二)

文章目录
- 1、求根节点到叶节点数字之和
- 2、二叉树剪枝
- 3、验证二叉搜索树
- 4、二叉搜索树中第K小的元素
- 5、二叉树的所有路径
1、求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。

class Solution {
public:int dfs(TreeNode* root,int presum){presum=presum*10+root->val;if(root->left==nullptr&&root->right==nullptr)return presum;int ret=0;if(root->left) ret+=dfs(root->left,presum);if(root->right) ret+=dfs(root->right,presum);return ret;}int sumNumbers(TreeNode* root) {return dfs(root,0);}
};
2、二叉树剪枝
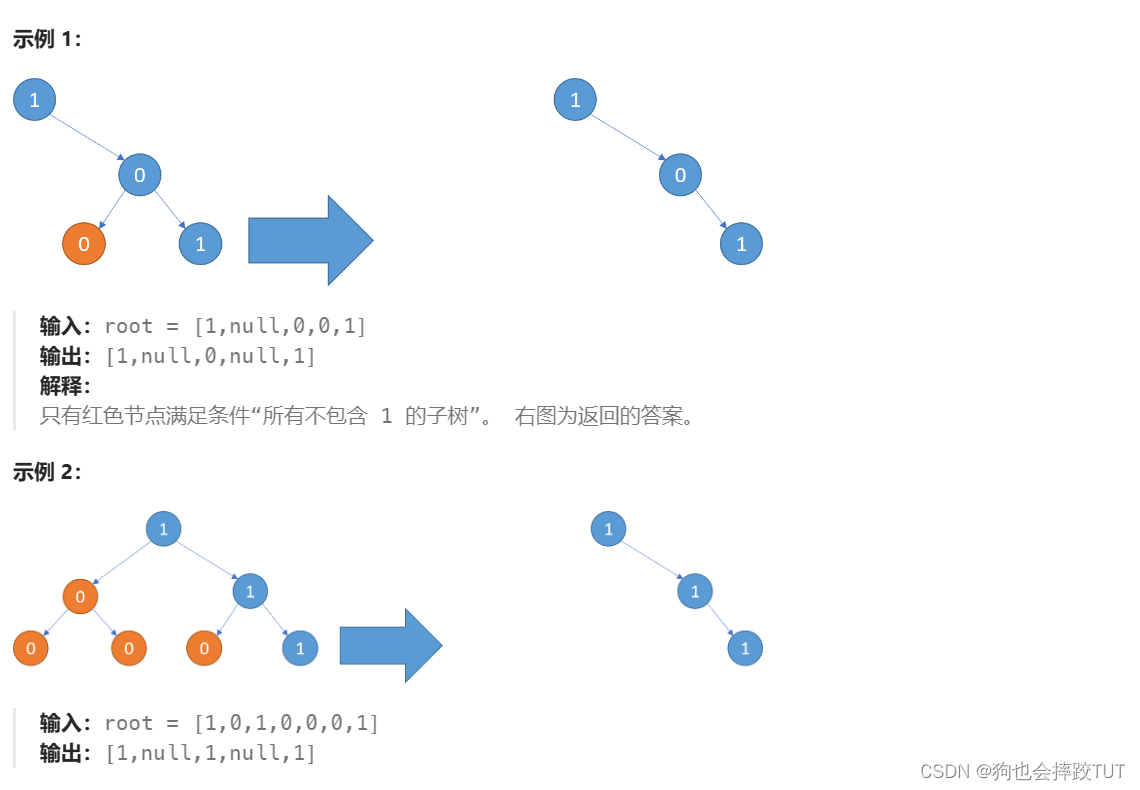
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
节点 node 的子树为 node 本身加上所有 node 的后代。
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root==nullptr)return nullptr;root->left=pruneTree(root->left);root->right=pruneTree(root->right);if(root->left==nullptr&&root->right==nullptr&&root->val==0){delete root;//可加可不加return nullptr;}return root;}
};
3、验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树
只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

class Solution {
public:long flag=LONG_MIN;bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);if(left==false) return false;//剪枝,作用为了提高效率bool cur=false;if(root->val>flag){ cur=true;flag=root->val;}if(cur==false) return false;//剪枝bool right=isValidBST(root->right);return left&&right&&cur;}
};
4、二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)

class Solution {
public:int count=0;int ret=0;void dfs(TreeNode* root,int k){if(root==nullptr||count==k)//count==0是剪枝return ;dfs(root->left,k);count++;if(count==k)ret=root->val;dfs(root->right,k);}int kthSmallest(TreeNode* root, int k) {dfs(root,k);return ret;}
};
5、二叉树的所有路径
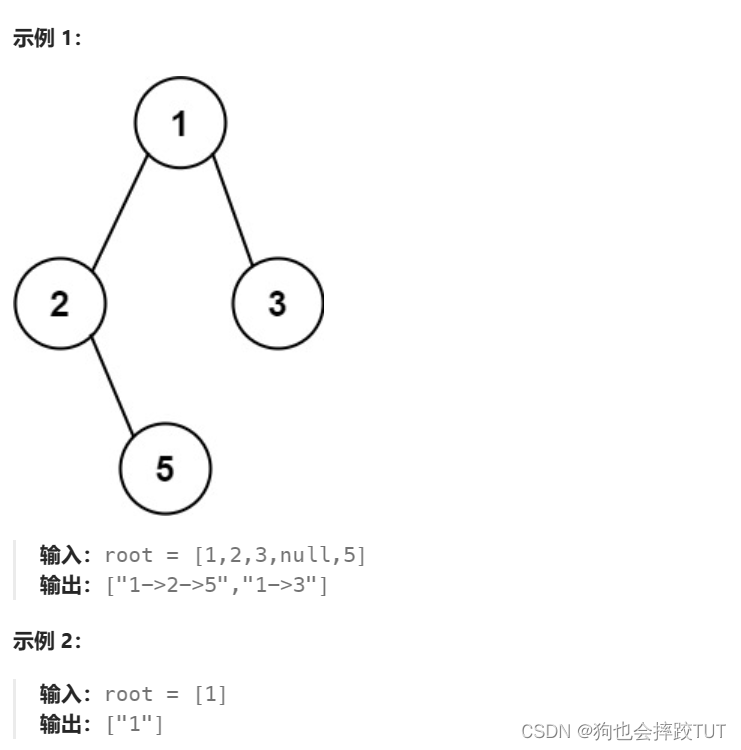
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
class Solution {
public:vector<string> dummy;void dfs(TreeNode* root,string str){str+=to_string(root->val);if(root->left==nullptr&&root->right==nullptr){dummy.push_back(str);return;}str+="->";if(root->left) dfs(root->left,str);//dfs(root->left,str);之前的操作是没有判断,不能只if(root->right) dfs(root->right,str);//判断root->left==nullptr&&root->right==nullptr,//还要想着单子树的问题,已经好几次了}vector<string> binaryTreePaths(TreeNode* root) {dfs(root,"");return dummy;}
};
相关文章:

【刷题篇】回溯算法(二)
文章目录 1、求根节点到叶节点数字之和2、二叉树剪枝3、验证二叉搜索树4、二叉搜索树中第K小的元素5、二叉树的所有路径 1、求根节点到叶节点数字之和 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...
Windows系统本地部署Jupyter Notebook并实现公网访问编辑笔记
文章目录 1.前言2.Jupyter Notebook的安装2.1 Jupyter Notebook下载安装2.2 Jupyter Notebook的配置2.3 Cpolar下载安装 3.Cpolar端口设置3.1 Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 在数据分析工作中,使用最多的无疑就是各种函数、图表、…...
Ansible 实战Shell 插件和模块工具)
自动化运维(二十七)Ansible 实战Shell 插件和模块工具
Ansible 支持多种类型的插件,这些插件可以帮助你扩展和定制 Ansible 的功能。每种插件类型都有其特定的用途和应用场景。今天我们一起学习Shell 插件和模块工具。 一、 Shell 插件 Ansible shell 插件决定了 Ansible 如何在远程系统上执行命令。这些插件非常关键&a…...

Jenkins使用-绑定域控与用户授权
一、Jenkins安装完成后,企业中使用,首先需要绑定域控以方便管理。 操作方法: 1、备份配置文件,防止域控绑定错误或授权策略选择不对,造成没办法登录,或登录后没有权限操作。 [roottest jenkins]# mkdir ba…...
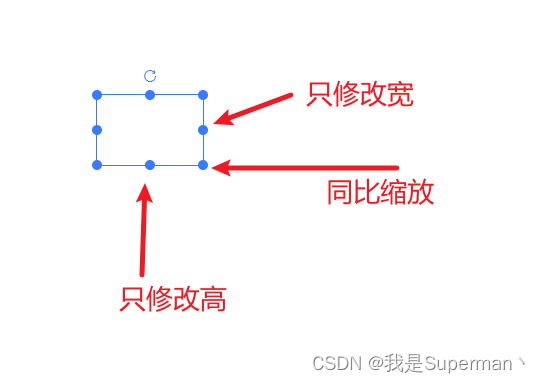
【前端】es-drager 图片同比缩放 缩放比 只修改宽 只修改高
【前端】es-drager 图片同比缩放 缩放比 ES Drager 拖拽组件 (vangleer.github.io) 核心代码 //初始宽 let width ref(108)//初始高 let height ref(72)//以下两个变量 用来区分是单独的修改宽 还是高 或者是同比 //缩放开始时的宽 let oldWidth 0 //缩放开始时的高 let o…...

蓝桥杯第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 A 组题解
1.幸运数 题目链接:0幸运数 - 蓝桥云课 (lanqiao.cn) #include<bits/stdc.h> using namespace std; bool deng(string& num){int n num.size();int qian 0,hou 0;for(int i0;i<n/2;i) qian (num[i]-0);for(int in/2;i<n;i) hou (num[i]-0);r…...
eclipse .project
.project <?xml version"1.0" encoding"UTF-8"?> <projectDescription> <name>scrm-web</name> <comment></comment> <projects> </projects> <buildSpec> <buil…...

react的闭包陷阱
React 的闭包陷阱是指在使用 React Hooks 时,由于闭包特性导致在某些函数或异步操作中无法正确访问到更新后状态或 prop 的值,而仍旧使用了旧值。下面通过几个代码示例来具体说明闭包陷阱的几种常见情形: 示例 1: useState 闭包陷阱 import…...

神经网络解决回归问题(更新ing)
神经网络应用于回归问题 优势是什么???生成数据集:通用神经网络拟合函数调整不同参数对比结果初始代码结果调整神经网络结构调整激活函数调整迭代次数增加早停法变量归一化处理正则化系数调整学习率调整 总结ingfnn.py进行计算&am…...

【小红书校招场景题】12306抢票系统
1 坐过高铁吧,有抢过票吗。你说说抢票系统对于后端开发人员而言会有哪些情况? 对于后端开发人员来说,开发和维护一个高铁抢票系统(如中国的12306)会面临一系列的挑战和情况。这些挑战主要涉及系统的性能、稳定性、数据…...
)
Spring(三)
1. Spring单例Bean是不是线程安全的? Spring单例Bean默认并不是线程安全的。由于多个线程可能访问同一份Bean实例,当Bean的内部包含了可变状态(mutable state)即有可修改的成员变量时,就可能出现线程安全问题。Spring容器不会自动…...

使用element-plus中的表单验证
标签页代码如下: // 注意:el-form中的数据绑定不可以用v-model,要使用:model <el-form ref"ruleFormRef" :rules"rules" :model"userTemp" label-width"80px"><el-row :gutter"20&qu…...

flinksql
Flink SQL 是 Apache Flink 项目中的一个重要组成部分,它允许开发者使用标准的 SQL 语言来处理流数据和批处理数据。Flink SQL 提供了一种声明式的编程范式,使得用户能够以一种简洁、高效且易于理解的方式来表达复杂的数据处理逻辑。 ### 背景 Flink SQL 的设计初衷是为了简…...

Dockerfile中 CMD和ENTRYPOINT的区别
在 Dockerfile 中,CMD 和 ENTRYPOINT 都用于指定容器启动时要执行的命令。它们之间的主要区别是: - CMD 用于定义容器启动时要执行的命令和参数,它设置的值可以被 Dockerfile 中的后续指令覆盖,包括在运行容器时传递的参数。如果…...

【TC3xx芯片】TC3xx芯片的总线内存保护
前言 广义上的内存保护,包括<<【TC3xx芯片】TC3xx芯片MPU介绍>>一文介绍的MPU(常规狭义上的内存保护),<<【TC3xx芯片】TC3xx芯片的Endinit功能详解>>一文中介绍的寄存器的EndInit保护,<<【TC3xx芯片】TC3xx芯片ACCEN寄存器保护详解>>一…...
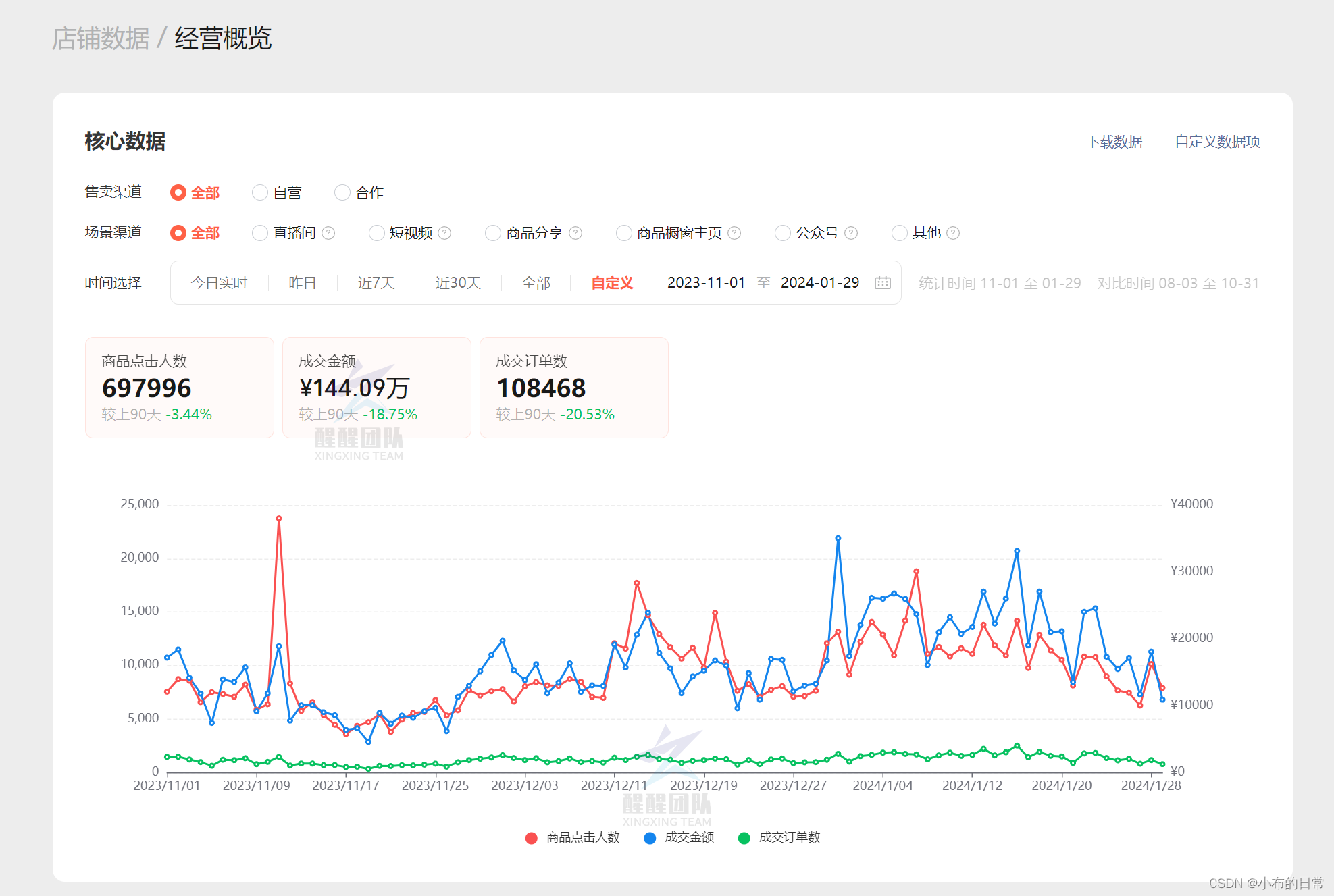
抖音小店选品必经五个阶段,看你到哪一步了,直接决定店铺爆单率
大家好,我是电商笨笨熊 新手选品必经的阶段就是迷茫期,不知道怎么选品,在哪里选品,选择什么样的品; 而有些玩家也会在进入店铺后疯狂选品,但是上架的商品没有销量; 而这些都是每个玩家都要经…...
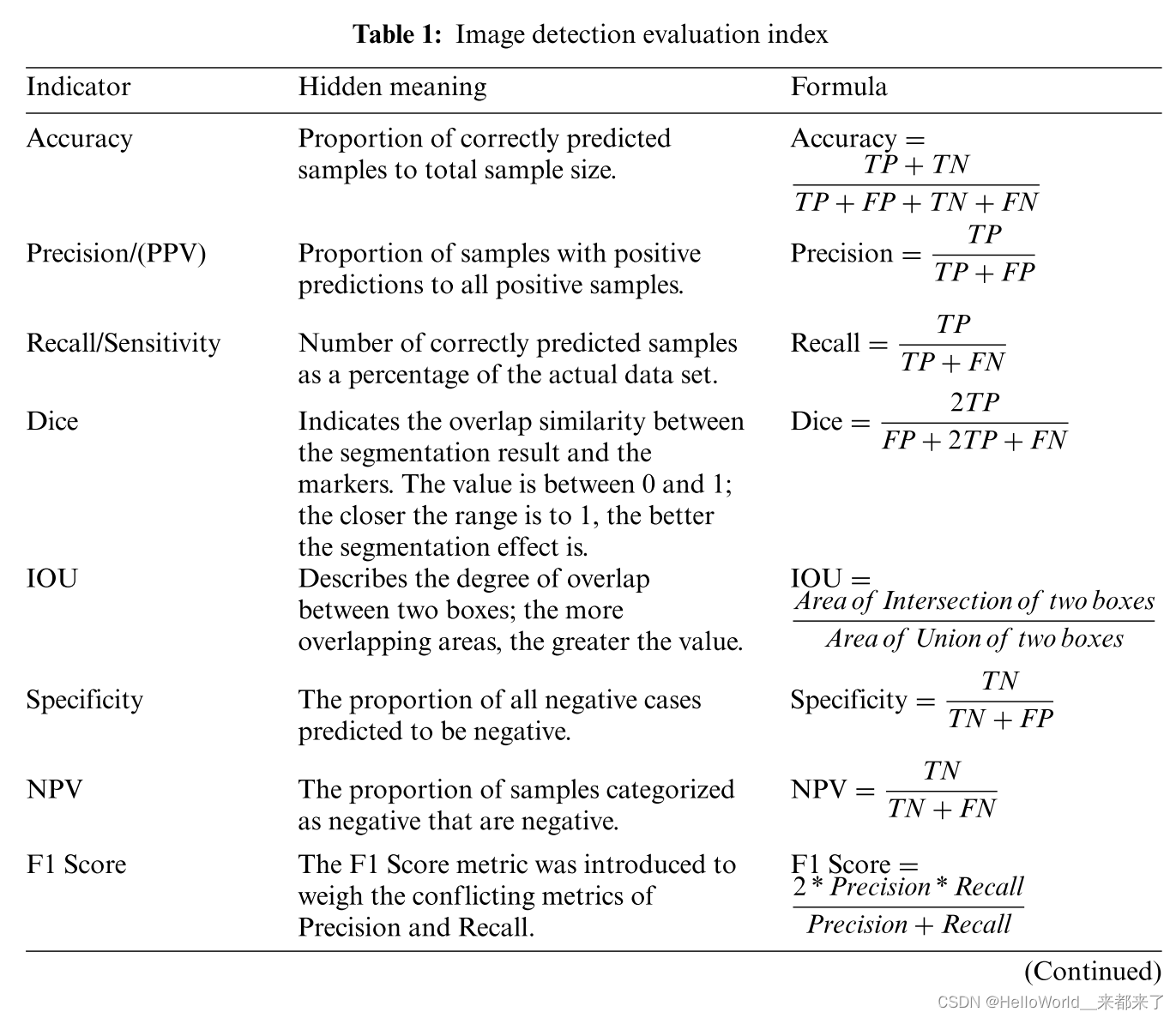
ML在骨科手术术前、书中、术后方法应用综述【含数据集】
达芬奇V手术机器人 近年来,人工智能(AI)彻底改变了人们的生活。人工智能早就在外科领域取得了突破性进展。然而,人工智能在骨科中的应用研究尚处于探索阶段。 本文综述了近年来深度学习和机器学习应用于骨科图像检测的最新成果,描述了其贡献、优势和不足。以及未来每项研究…...

vue3-video-play 在安卓上正常播放,在ios上不能播放,问题解决
1.ios上autoplay需要静音,在播放后再打开声音 <vue3videoPlay v-if"!isComponent" v-bind"options" :playsinline"playsinline"></vue3videoPlay>let playsinline computed(() > {if (props.isComponent) {return}o…...
【C++类和对象】上篇
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...

微信订阅号环境搭建及开发者工具下载
目录 一、注册订阅号 1.1 选择注册 2.2 选择订阅号注册 1.3 登录进入主页面 编辑 1.4 可以进行自定义菜单 1.5 我们重点关注公众平台测试账号 编辑 1.6 自定义一个域名 1.7 用自己的微信扫描这个二维码 编辑 1.8 点击修改,并自定义个域名 二、开发…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
