力扣刷题 二叉树层序遍历相关题目II
NO.116 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
本题难点在于如何填充每个节点的next 指针,让这个指针指向其下一个右侧节点。如何获取队列中下一个节点,我们还没有遍历到下一个节点,怎么能获取下一个节点的指针呢?
这里的思路是保存上一个遍历节点的指针,让它的next指针指向当前节点。是不是很巧妙,和我们自然的思路不太一样。
因为我们用到了前节点的变量,而头节点并没有前节点,所以需要单独考虑情况。
完整代码如下
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();//建立当前节点Node* node;Node* prenode;// 遍历队列,放入数组for(int i = 0; i < size; i++ ){//如果遍历到这一层的头节点if(i == 0){node = que.front();prenode = node;}else{//出队列第一个元素放入数组node = que.front();//上一个节点的next指针指向当前节点prenode->next = node;//将前节点更新为当前节点prenode = node;}//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();}//这一层遍历完,将最后一个元素的next设置为nullnode->next = NULL;}return root;}
};总结与反思
层序遍历最关键的是深刻理解整个for循环是每一层遍历的核心,这样添加代码就会更加自如,知道是在层前还是层中还是层后。
写完代码,可以验证一遍测试用例,发现bug,避免显而易见的错误。
NO.117 填充每个节点的下一个右侧节点指针II
给定一个二叉树:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:
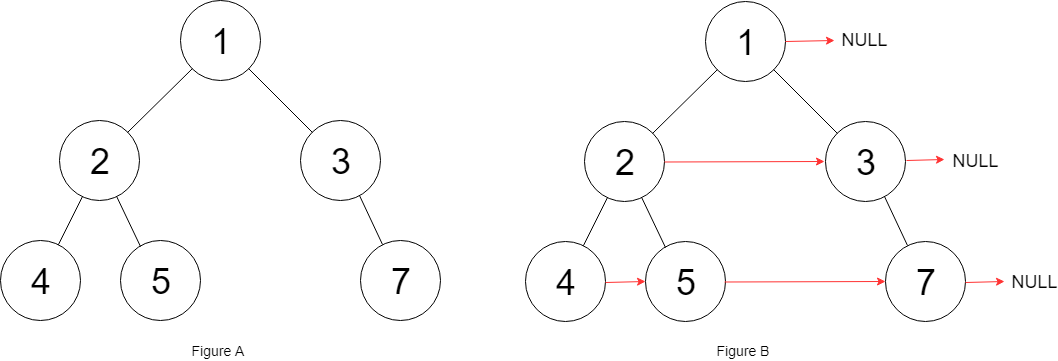
输入:root = [1,2,3,4,5,null,7] 输出:[1,#,2,3,#,4,5,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = [] 输出:[]
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
完整代码如下
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();//建立当前节点Node* node;Node* prenode;// 遍历队列,放入数组for(int i = 0; i < size; i++ ){//如果遍历到这一层的头节点if(i == 0){node = que.front();prenode = node;}else{//出队列第一个元素放入数组node = que.front();//上一个节点的next指针指向当前节点prenode->next = node;//将前节点更新为当前节点prenode = node;}//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();}//这一层遍历完,将最后一个元素的next设置为nullnode->next = NULL;}return root;}
};NO.104 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
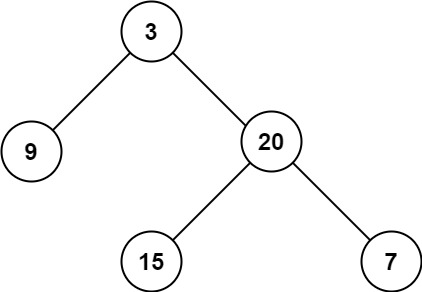
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
完整代码如下
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;//记录最大深度int depth = 0;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();// 遍历队列,放入数组for(int i = 0; i < size; i++ ){TreeNode* node = que.front();//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();} depth++;}//循环结束说明遍历完最后一层,返回深度return depth;}
};NO.111 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
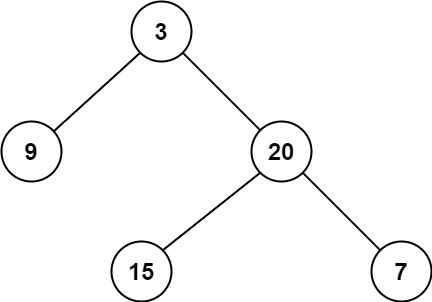
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
完整代码如下
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> que;//记录深度int depth = 0;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();// 遍历队列,放入数组depth++;for(int i = 0; i < size; i++ ){TreeNode* node = que.front();//一旦找到叶子节点就返回深度if(node->left == NULL && node->right == NULL) return depth;//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();} }return 0;}
};相关文章:

力扣刷题 二叉树层序遍历相关题目II
NO.116 填充每个节点的下一个右侧节点指针 给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下: struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针,…...

智能电网将科技拓展至工厂之外的领域
【摘要/前言】 物联网已然颠覆我们日常生活的许多层面。在家居方面,家电变成连网设备,不仅让我们能控制灯光与上网购物,甚至在出门时提供安全功能。在工业领域,智能工厂改变产品制造的方式。工业物联网(IIoT)不仅让制造商更加敏捷…...

单列模式1.0
单列模式 单例模式能保证某个类在程序中只存在唯⼀⼀份实例, ⽽不会创建出多个实例 1.饿汉模式 只要程序一启动就会立即创建出一个对象 class Signleton{private static Signleton instancenew Signleton();//防止在以后的代码中再创建对象,我们将构造方法private,…...

golang kafka sarama源码分析
一些理论 1.topic支持多分区,每个分区只能被组内的一个消费者消费,一个消费者可能消费多个分区的数据; 2.消费者组重平衡的分区策略,是由消费者自己决定的,具体是从消费者组中选一个作为leader进行分区方案分配&#…...
计算机组成原理【CO】Ch2 数据的表示和应用
文章目录 大纲2.1 数制与编码2.2 运算方法和运算电路2.3 浮点数的表示和运算 【※】带标志加法器OFSFZFCF计算机怎么区分有符号数无符号数? 【※】存储排列和数据类型转换数据类型大小数据类型转换 进位计数制进制转换2的次幂 各种码的基本特性无符号整数的表示和运算带符号整…...

dfs回溯 -- Leetcode46. 全排列
题目链接:46. 全排列 题目描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示…...
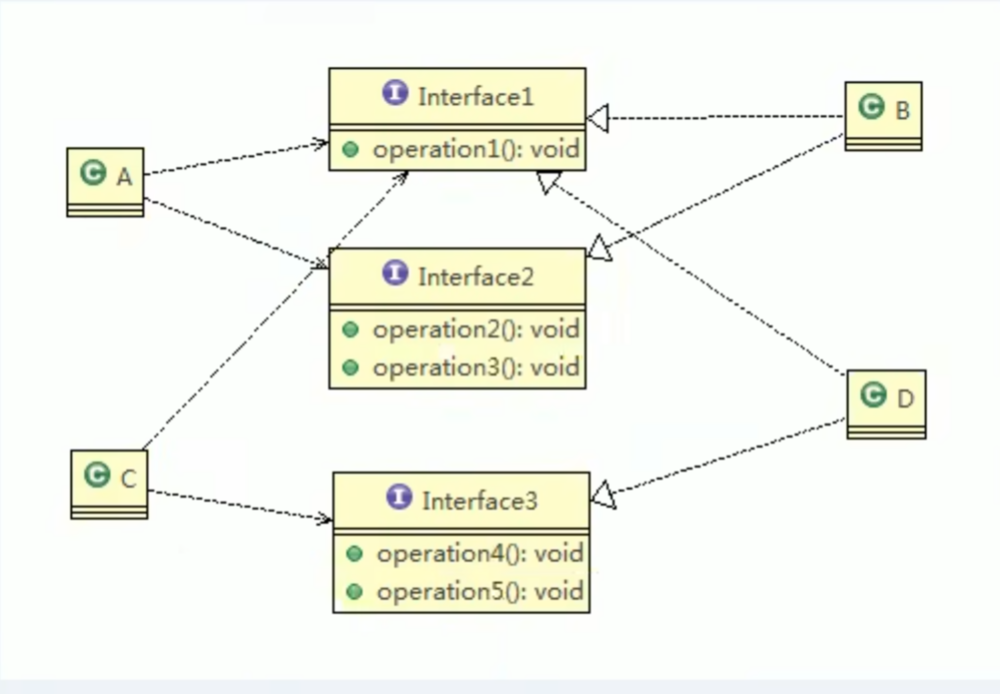
设计模式-接口隔离原则
基本介绍 客户端不应该依赖它不需要的接口,即一个类对另一个类的依赖应该建立在最小的接口上先看一张图: 类A通过接口Interface1 依赖类B,类C通过接口Interface1 依赖类D,如果接口Interface1对于类A和类C来说不是最小接口,那么类…...
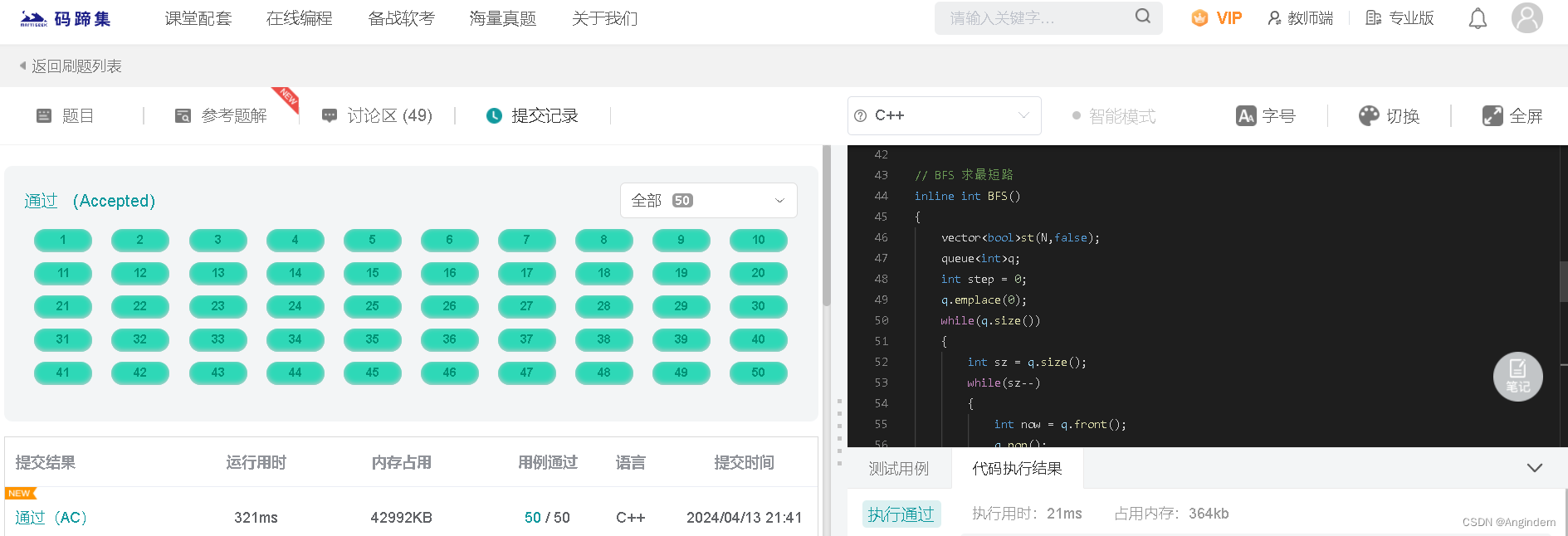
BD202311夏日漫步(最少步数,BFS或者 Dijstra)
本题链接:码蹄集 题目: 夏日夜晚,小度看着庭院中长长的走廊,萌发出想要在上面散步的欲望,小度注意到月光透过树荫落在地砖上,并且由于树荫的遮蔽度不通,所以月光的亮度不同,为了直…...

React - 你知道props和state之间深层次的区别吗
难度级别:初级及以上 提问概率:60% 如果把React组件看做一个函数的话,props更像是外部传入的参数,而state更像是函数内部定义的变量。那么他们还有哪些更深层次的区别呢,我们来看一下。 首先说props,他是组件外部传入的参数,我们知道…...
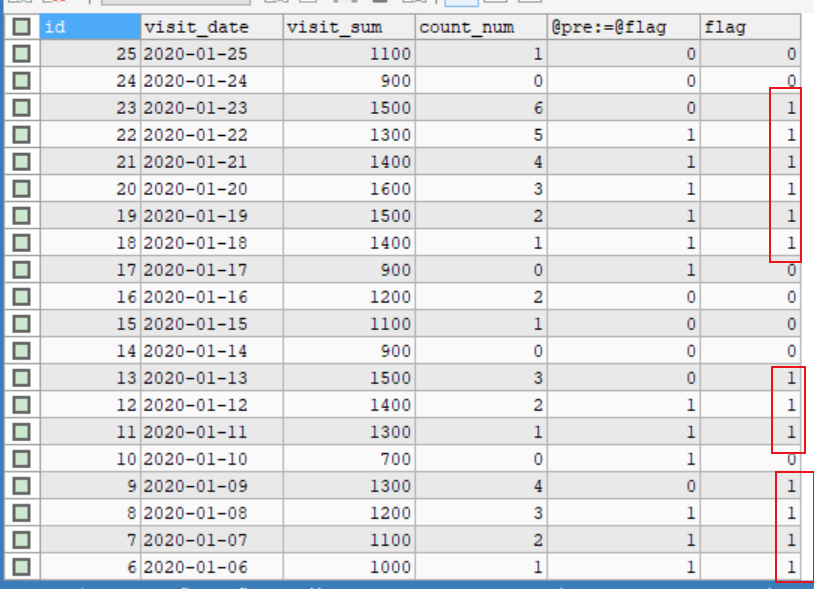
mysql 查询实战-变量方式-解答
对mysql 查询实战-变量方式-题目,进行一个解答。(先看题,先做,再看解答) 1、查询表中⾄少连续三次的数字 1,处理思路 要计算连续出现的数字,加个前置变量,记录上一个的值,…...

SpringBoot3配置SpringSecurity6
访问1:localhost:8080/security,返回:需要先认证才能访问(说明没有权限) 访问2:localhost:8080/anonymous,返回:anonymous(说明正常访问) 相关文件如下&…...
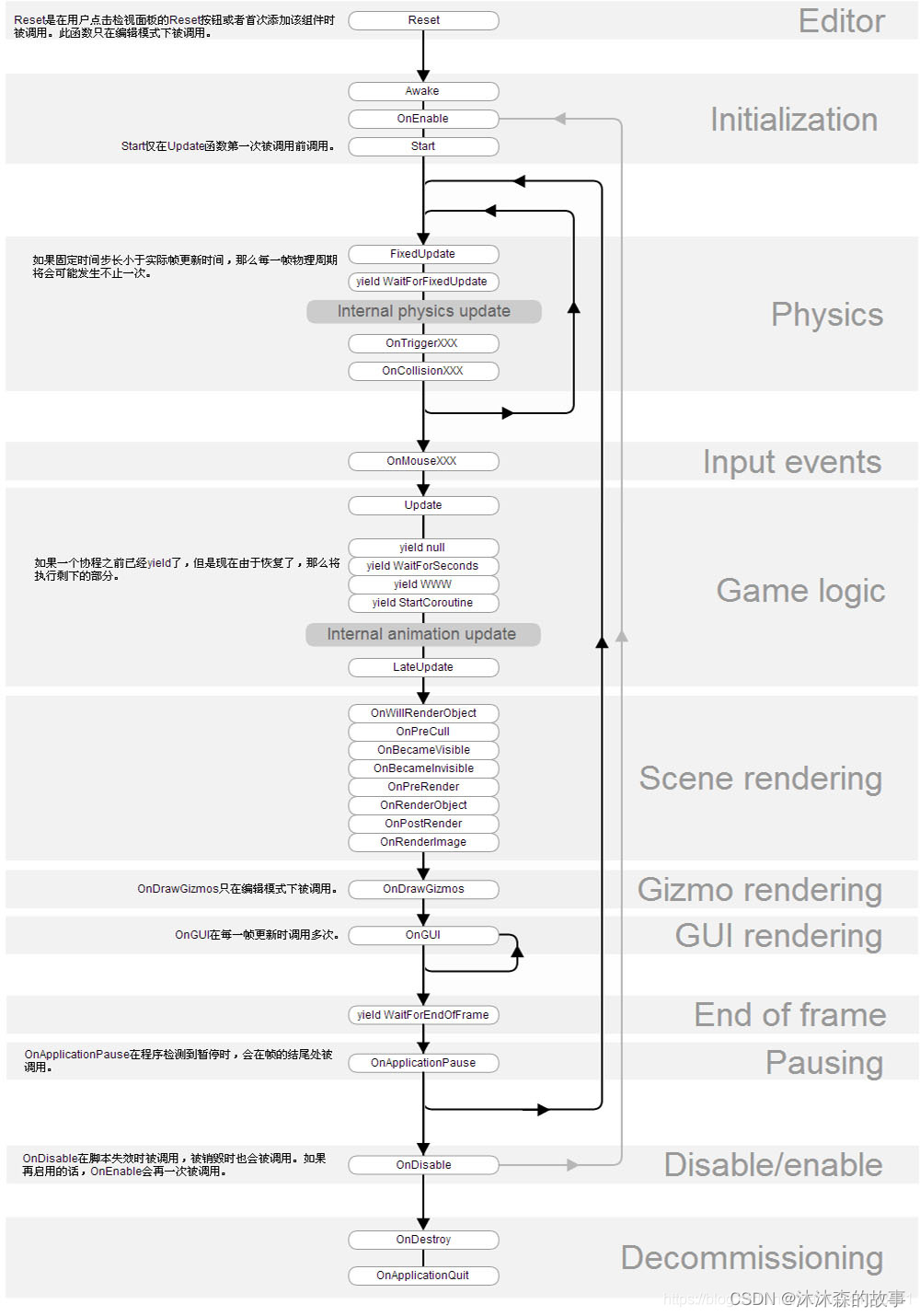
Unity之Unity面试题(三)
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity之Unity面试题(三) TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进取…...
)
Linux命令-dos2unix命令(将DOS格式文本文件转换成Unix格式)
说明 dos2unix命令 用来将DOS格式的文本文件转换成UNIX格式的(DOS/MAC to UNIX text file format converter)。DOS下的文本文件是以 \r\n 作为断行标志的,表示成十六进制就是0D0A。而Unix下的文本文件是以\n作为断行标志的,表示成…...

企业怎么做数据分析
数据分析在当今信息化时代扮演着至关重要的角色。能够准确地收集、分析和利用数据,对企业的决策和发展都具有重要意义。数聚将介绍企业如何合理地利用数据分析,如何协助企业在竞争激烈的市场中取得优势。 一、建立完善的数据收集系统 在进行数据分析之…...

1111111111
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...
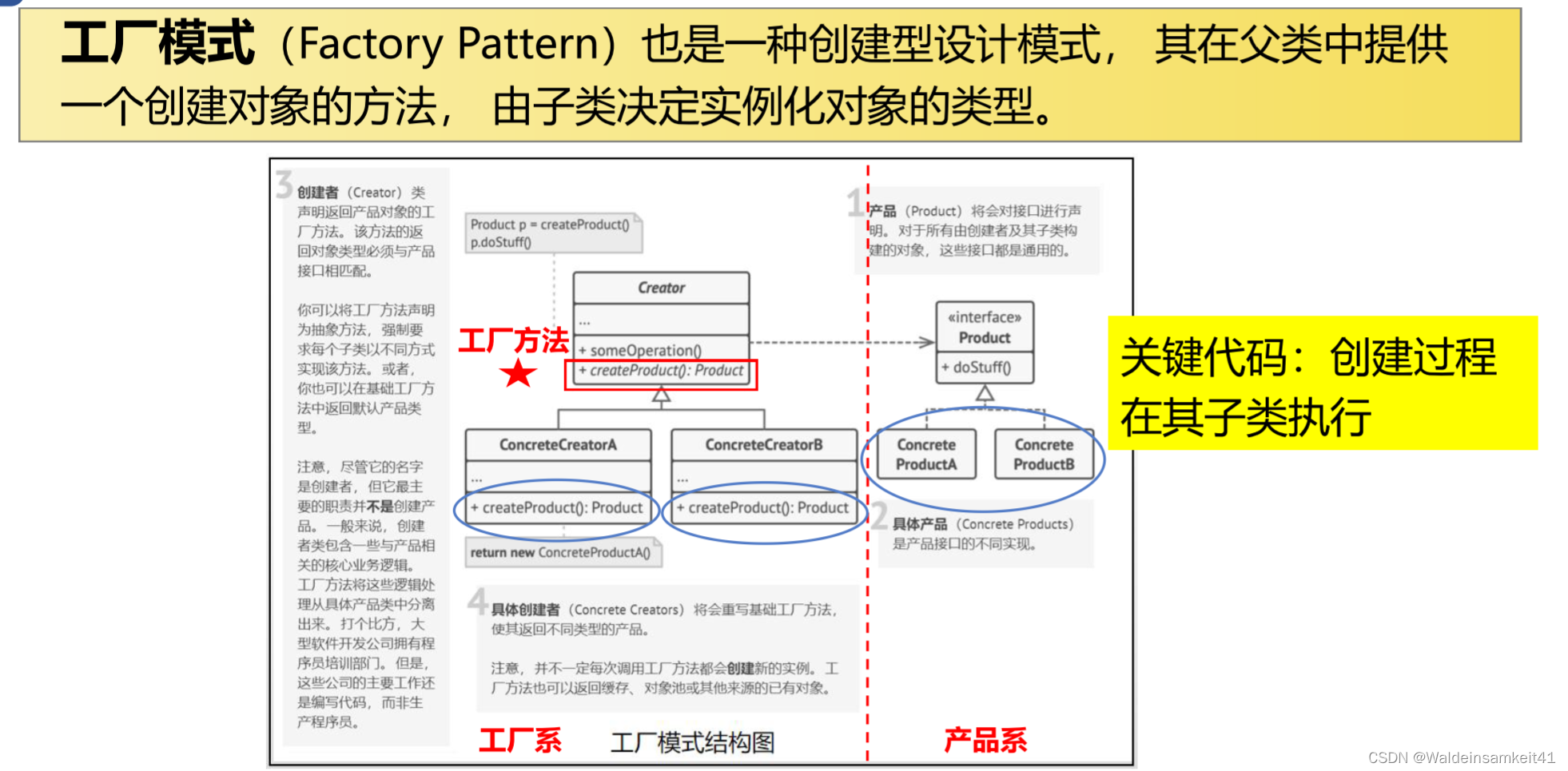
[面向对象] 单例模式与工厂模式
单例模式 是一种创建模式,保证一个类只有一个实例,且提供访问实例的全局节点。 工厂模式 面向对象其中的三大原则: 单一职责:一个类只有一个职责(Game类负责什么时候创建英雄机,而不需要知道创建英雄机要…...
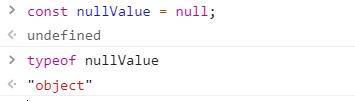
《前端防坑》- JS基础 - 你觉得typeof nullValue === null 么?
问题 JS原始类型有6种Undefined, Null, Number, String, Boolean, Symbol共6种。 在对原始类型使用typeof进行判断时, typeof stringValue string typeof numberValue number 如果一个变量(nullValue)的值为null,那么typeof nullValue "?" const u …...
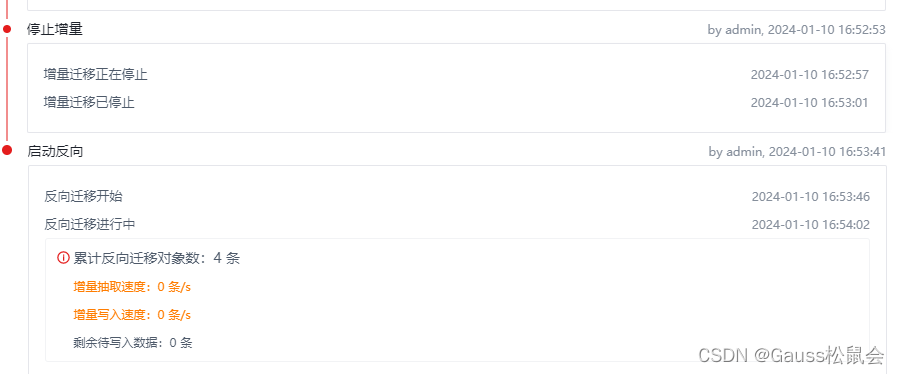
【项目实战经验】DataKit迁移MySQL到openGauss(下)
上一篇我们分享了安装、设置、链接、启动等步骤,本篇我们将继续分享迁移、启动~ 目录 9. 离线迁移 9.1. 迁移插件安装 中断安装,比如 kill 掉java进程(安装失败也要等待300s) 下载安装包准备上传 缺少mysqlclient lib包 mysq…...
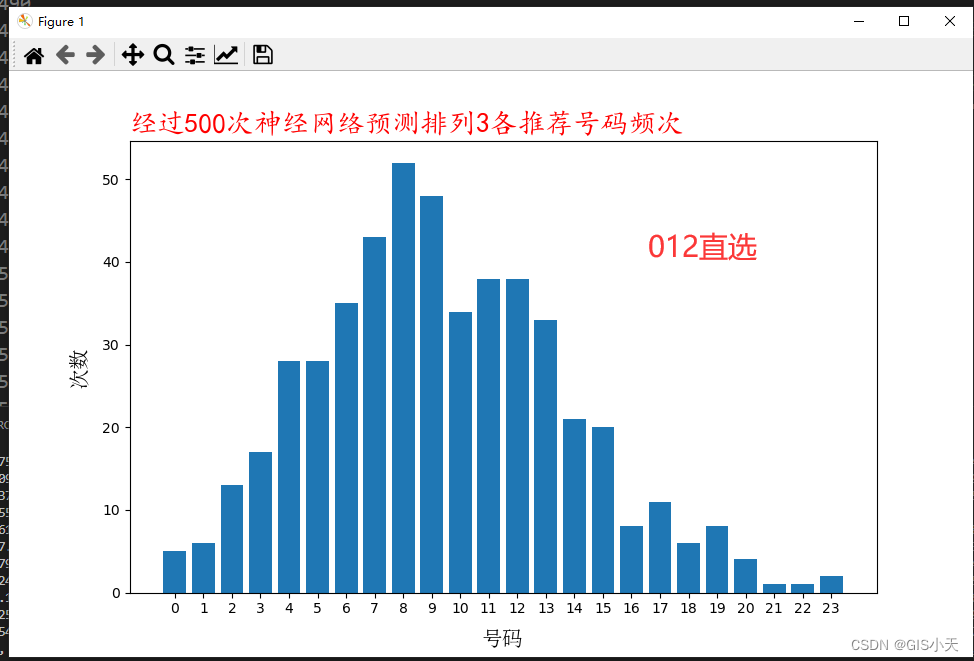
AI预测体彩排3第2弹【2024年4月13日预测--第1套算法开始计算第2次测试】
各位小伙伴,今天实在抱歉,周末回了趟老家,回来比较晚了,数据今天上午跑完后就回老家了,晚上8点多才回来,赶紧把预测结果发出来吧,虽然有点晚了,但是咱们前面说过了,目前的…...
2024年4月串讲题组一)
【13137】质量管理(一)2024年4月串讲题组一
目录 1.选择题 2.多选题 3.简答题 4.论述题 5.计算题 6.论述题 【13137】质量管理-速 记 宝 典【全国通用】</...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
