视觉SLAM学习打卡【10】-后端·滑动窗口法位姿图
- 本节是对上一节BA的进一步简化,旨在提高优化实时性.
- 难点在于位姿图部分的雅可比矩阵求解(涉及李代数扰动模型求导),书中的相关推导存在跳步(可能数学功底强的人认为过渡的理所当然),笔者参考了知乎Clark的推导,并以顺向思维的方式重新整理推导过程,使得该部分更加通俗易懂.
视觉SLAM学习打卡【10】-后端·滑动窗口法&位姿图
- 一、本讲缘由
- 二、滑动窗口法
- (1)某个时刻窗口的优化处理
- (2)窗口滑动,结构发生改变
- 三、位姿图
- 四、实践g2o_viewer报错解决方案
一、本讲缘由
接上节 视觉SLAM学习打卡【9】-后端·卡尔曼滤波器&光束法平差,BA能同时优化位姿与空间点。然而,大量的路标点/特征点,使得计算量增大,实时性降低。本讲致力于控制BA的规模。
- 滑动窗口法(Sliding Window):将BA控制在一个时间窗口中,离开窗口的关键帧被丢弃.
- 共视图(Covisibility graph):与当前相机存在共同观测的关键帧构成的图像即为共视图。仅优化与当前帧有20个以上共视路标的关键帧,其余固定不变.
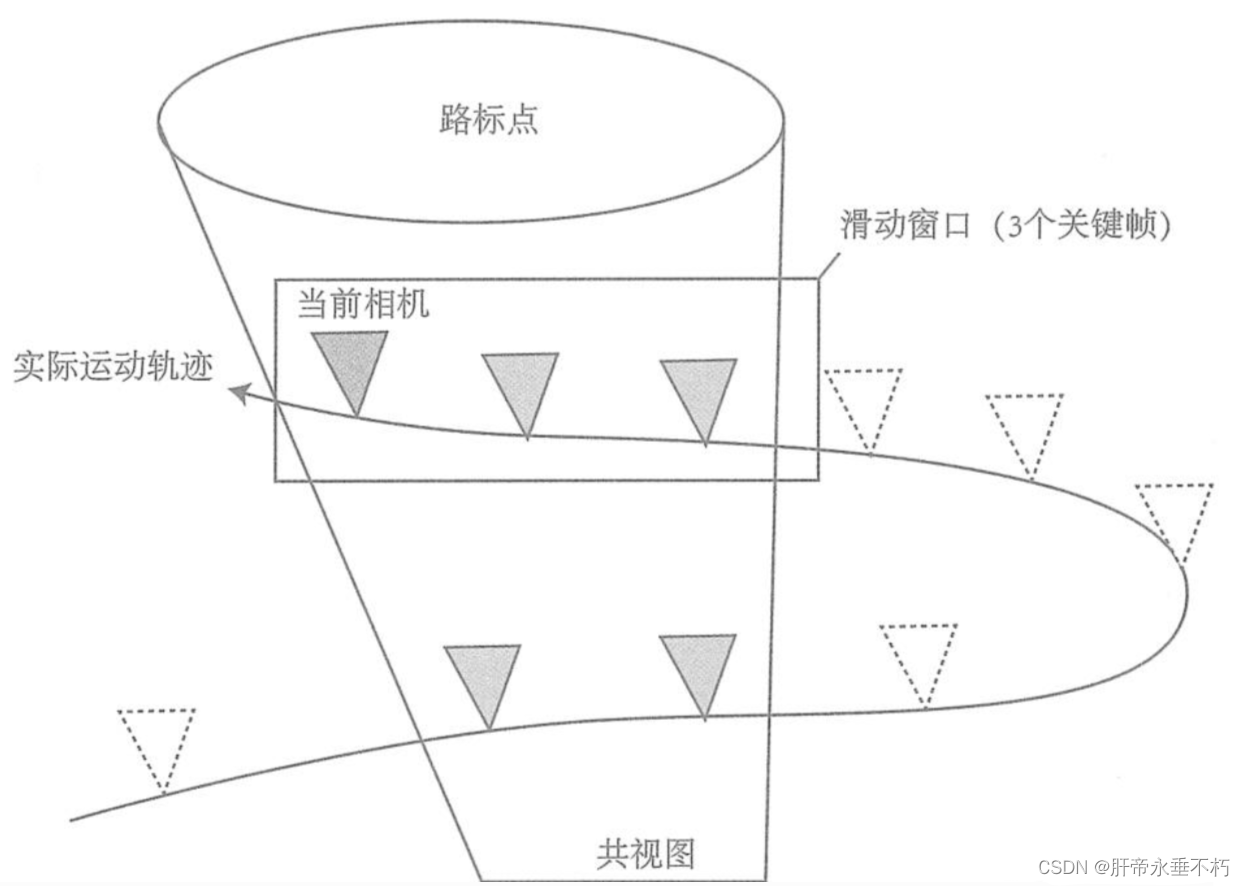
- 位姿图(Pose Graph):不管路标,只管轨迹,构建一个只有轨迹的图优化.
二、滑动窗口法
仅保留离当前时刻最近的 N个关键帧(从连续视频中抽出的一部分图像),去掉时间上最早的关键帧。于是BA被固定在一个时间窗口内,离开这个窗口则被丢弃,这种方法称为滑动窗口法。
(1)某个时刻窗口的优化处理
假设此时这个窗口内有 N 个关键帧和M个路标点.
- 关键帧位姿表达为: x 1 , ⋯ , x N x_1,\cdots,x_N x1,⋯,xN
- 路标点为: y 1 , ⋯ , y M y_1,\cdots,y_M y1,⋯,yM
用上一讲BA方法处理这个滑动窗口,包括建立最小二乘问题,构建整体的Hessian海森矩阵,然后边缘化所有路标点来加速求解。
最后,优化结果为: [ x 1 , ⋯ , x N ] T ∼ N ( [ μ 1 , ⋯ , μ N ] T , Σ ) [x_1,\cdots,x_N]^T\sim N([\mu_1,\cdots,\mu_N]^T,\Sigma) [x1,⋯,xN]T∼N([μ1,⋯,μN]T,Σ)
其中,均值部分 μ k \mu_{k} μk为为第 k个关键帧的位姿均值,即BA迭代之后的结果;所有关键帧的协方差矩阵 Σ \Sigma Σ是对整个 BA 的 H 矩阵进行舒尔消元边缘化后的系数矩阵.
(2)窗口滑动,结构发生改变
滑动中,状态变量的更新讨论:
- 新增一个关键帧和对应观测到的路标点
类似于(1),BA (N+1) 个关键帧和对应的路标点. - 删除 / 边缘化一个旧的关键帧
删除旧关键帧 x1,将 x1 边缘化之后将导致整个问题不再稀疏,将破坏路标部分的对角块结构.
当边缘化路标点时,S= [ B − E C − 1 E T 0 E T C ] \begin{bmatrix}B-EC^{-1}E^\mathrm{T}&0\\E^\mathrm{T}&C\end{bmatrix} [B−EC−1ETET0C],Fill-in将出现在左上角的位姿块中,右下角的路标块仍为对角阵,保持稀疏,不影响求解
当边缘化关键帧时,Fill-in将出现在右下角的路标块中,BA无法按照之前的稀疏方式迭代求解.
解决方法:边缘化关键帧的同时,边缘化它观测到的路标点,保持了右下角的对角块结构。在OKVIS中,根据要边缘化的关键帧所看到的路标点是否在最新的关键帧中能看到来考虑是否边缘化此路标点。如果不能,就直接边缘化这个路标点;如果能,就丢弃被边缘化关键帧对这个路标点的观测,从而保持BA的稀疏性。
三、位姿图
构建一个只有轨迹的图优化,而位姿节点之间的边,可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初值(对极几何 / PnP / ICP)。不同的是,一旦初始估计完成,就不再优化那些路标点的位置,而只关心所有的相机位姿之间的联系,省去了大量特征点优化的计算,只保留了关键帧的轨迹,从而构建了所谓的位姿图.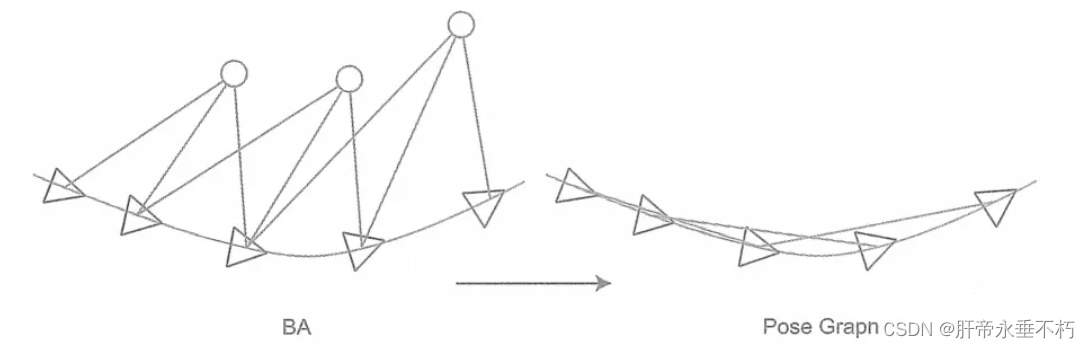
图优化中,节点表示相机位姿,以 T 1 , ⋯ , T n T_1,\cdots,T_n T1,⋯,Tn表示;边是两个位姿节点之间相对运动的估计(特征点法/直接法/GPS / IMU积分)
GPS通过连续测量两个位姿节点在不同时间点的绝对位置,进而通过比较这些位置数据来间接估计它们之间的相对运动。
IMU积分通过测量和跟踪物体的加速度和角速度,并对其进行积分运算,从而估计出两个位姿节点之间的相对运动。
估计 T i T_{i} Ti和 T j T_{j} Tj之间的运动 Δ T i j \Delta T_{ij} ΔTij,李群写法: Δ T i j = T i − 1 T j ΔT_{ij}=T_i^{-1}T_j ΔTij=Ti−1Tj李代数写法: Δ ξ i j = ξ i − 1 ∘ ξ j = ln ( T i − 1 T j ) ∨ \Delta\xi_{ij}=\xi_i^{-1}\circ\xi_j=\ln(T_i^{-1}T_j)^\vee Δξij=ξi−1∘ξj=ln(Ti−1Tj)∨构建误差 e i j e_{ij} eij: e i j = ln ( T i j − 1 T i − 1 T j ) ∨ = l n ( I ) = 0 e_{ij}=\ln(T_{ij}^{-1}T_i^{-1}T_j)^\vee= ln(I)=0 eij=ln(Tij−1Ti−1Tj)∨=ln(I)=0优化变量有两个 ξ i \xi_{i} ξi和 ξ j \xi_{j} ξj,求 e i j e_{ij} eij关于这两个变量的导数(利用扰动模型,给 ξ i \xi_{i} ξi和 ξ j \xi_{j} ξj各乘一个左扰动 δ ξ i \delta\xi_{i} δξi和 δ ξ j \delta\xi_{j} δξj): e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) exp ( δ ξ j ∧ ) T j ) ∨ \hat{e}_{ij}=\ln(T_{ij}^{-1}T_i^{-1}\exp((-\delta\xi_i)^{\wedge})\exp(\delta\xi_j^{\wedge})T_j)^{\vee} e^ij=ln(Tij−1Ti−1exp((−δξi)∧)exp(δξj∧)Tj)∨
其中, δ ξ i \delta\xi_{i} δξi乘左扰动到了右边,是因为逆的存在 ( exp ( δ ξ i ∧ ) T i ) − 1 = T i − 1 ⋅ ( exp ( δ ξ i ∧ ) ) − 1 = T i − 1 ⋅ exp ( − δ ξ i ∧ ) \begin{aligned}&(\exp(\delta\xi_{i}^{\wedge})T_{i})^{-1}\\&=T_{i}^{-1}\cdot(\exp(\delta\xi_{i}^{\wedge}))^{-1}\\&=T_{i}^{-1}\cdot \exp(-\delta\xi_{i}^{\wedge})\end{aligned} (exp(δξi∧)Ti)−1=Ti−1⋅(exp(δξi∧))−1=Ti−1⋅exp(−δξi∧)
根据伴随性质公式 exp ( ( A d ( T ) ξ ) ∧ ) = T exp ( ξ ∧ ) T − 1 \exp((Ad(T)\xi)^{\wedge})=T\exp(\xi^{\wedge})T^{-1} exp((Ad(T)ξ)∧)=Texp(ξ∧)T−1 (其中, A d ( T ) = [ R t ∧ R 0 R ] Ad(T)=\begin{bmatrix}R&t^\wedge R\\\mathbf{0}&R\end{bmatrix} Ad(T)=[R0t∧RR])的变形 exp ( ξ ∧ ) T = T exp ( ( A d ( T − 1 ) ξ ) ∧ ) \exp(\xi^\wedge)T=T\exp((Ad(T^{-1})\xi)^\wedge) exp(ξ∧)T=Texp((Ad(T−1)ξ)∧) ,把扰动项挪到最右边: e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) exp ( δ ξ j ∧ ) T j ⏟ 伴随性质 ) ∨ = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) T j exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) ⏞ ) ∨ = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) T j ⏟ 伴随性质 exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) ∨ = ln ( T i j − 1 T i − 1 T j exp ( ( − A d ( T j − 1 ) δ ξ i ) ∧ ) ⏞ exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) ) ∨ \begin{aligned} \hat{e}_{ij}& =\ln\left(T_{ij}^{-1}T_{i}^{-1}\exp\left((-\delta\xi_{i})^{\wedge}\right)\underbrace{\exp(\delta\xi_{j}^{\wedge})T_{j}}_{\text{伴随性质}}\right)^{\vee} \\ &=\ln\left(T_{ij}^{-1}T_i^{-1}\exp((-\delta\xi_i)^\wedge)\overbrace{T_j\exp((Ad(T_j^{-1})\delta\xi_j)^\wedge)}\right)^\vee \\ &=\ln\left(T_{ij}^{-1}T_i^{-1}\underbrace{\exp\left((-\delta\xi_i)^\wedge\right)T_j}_\text{伴随性质}\exp\left((Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right)^\vee \\ &=\ln\left(T_{ij}^{-1}T_i^{-1}\overbrace{T_j\exp\left(\left(-Ad(T_j^{-1})\delta\xi_i\right)^{\wedge}\right)}\exp\left(\left(Ad(T_j^{-1})\delta\xi_j\right)^{\wedge}\right)\right)^{\vee} \end{aligned} e^ij=ln Tij−1Ti−1exp((−δξi)∧)伴随性质 exp(δξj∧)Tj ∨=ln(Tij−1Ti−1exp((−δξi)∧)Tjexp((Ad(Tj−1)δξj)∧) )∨=ln Tij−1Ti−1伴随性质 exp((−δξi)∧)Tjexp((Ad(Tj−1)δξj)∧ ∨=ln(Tij−1Ti−1Tjexp((−Ad(Tj−1)δξi)∧) exp((Ad(Tj−1)δξj)∧))∨
对上述指数 exp ( ( − A d ( T j − 1 ) δ ξ i ) ∧ ) \exp\left(\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge\right) exp((−Ad(Tj−1)δξi)∧)和 exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) \exp\left(\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right) exp((Ad(Tj−1)δξj)∧)分别做泰勒一阶展开: exp ( ( − A d ( T j − 1 ) δ ξ i ) ∧ ) = I + ( − A d ( T j − 1 ) δ ξ i ) ∧ exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) = I + ( A d ( T j − 1 ) δ ξ j ) ∧ \exp\left(\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge\right)=I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge\\\exp\left(\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right)=I+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge exp((−Ad(Tj−1)δξi)∧)=I+(−Ad(Tj−1)δξi)∧exp((Ad(Tj−1)δξj)∧)=I+(Ad(Tj−1)δξj)∧忽略二次项得: exp ( ( − A d ( T j − 1 ) δ ξ i ) ∧ ) exp ( ( A d ( T j − 1 ) δ ξ j ) ∧ ) ≈ ( I + ( − A d ( T j − 1 ) δ ξ i ) ∧ ) ( I + ( A d ( T j − 1 ) δ ξ j ) ∧ ) ≈ I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ + ( − A d ( T j − 1 ) δ ξ i ) ∧ ( A d ( T j − 1 ) δ ξ j ) ∧ ⏟ 二次项忽略不计 = I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ \begin{aligned} \exp\left(\left(-Ad(T_{j}^{-1})\delta\xi_{i}\right)^{\wedge}\right)\exp\left(\left(Ad(T_{j}^{-1})\delta\xi_{j}\right)^{\wedge}\right)& \approx\left(I+\left(-Ad(T_{j}^{-1})\delta\xi_{i}\right)^{\wedge}\right)\left(I+\left(Ad(T_{j}^{-1})\delta\xi_{j}\right)^{\wedge}\right) \\ &\approx I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^{\wedge}+\left(Ad(T_j^{-1})\delta\xi_j\right)^{\wedge} \\ &+\underbrace{{\left(-Ad(T_{j}^{-1})\delta\xi_{i}\right)^{\wedge}\left(Ad(T_{j}^{-1})\delta\xi_{j}\right)^{\wedge}}}_{\text{二次项忽略不计}} \\ &=I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^{\wedge}+\left(Ad(T_j^{-1})\delta\xi_j\right)^{\wedge} \end{aligned} exp((−Ad(Tj−1)δξi)∧)exp((Ad(Tj−1)δξj)∧)≈(I+(−Ad(Tj−1)δξi)∧)(I+(Ad(Tj−1)δξj)∧)≈I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧+二次项忽略不计 (−Ad(Tj−1)δξi)∧(Ad(Tj−1)δξj)∧=I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧
e ^ i j ≈ ln ( T i j − 1 T i − 1 T j [ I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ ] ) ∨ \hat{e}_{ij}\approx\ln\left(T_{ij}^{-1}T_i^{-1}T_j\left[I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right]\right)^\vee e^ij≈ln(Tij−1Ti−1Tj[I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧])∨
- 令变换矩阵 T i j − 1 T i − 1 T j T_{ij}^{-1}T_i^{-1}T_j Tij−1Ti−1Tj对应的李代数为 e i j e_{ij} eij,根据李群李代数的对应关系得: T i j − 1 T i − 1 T j = exp ( e i j ∧ ) T_{ij}^{-1}T_i^{-1}T_j=\exp(e_{ij}^{\wedge}) Tij−1Ti−1Tj=exp(eij∧)
- 再令 exp ( x ∧ ) = I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ \exp(x^\wedge)=I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge exp(x∧)=I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧根据对数函数的泰勒展开式: ln ( A ) = ( A − I ) − ( A − I ) 2 2 + ( A − I ) 3 3 − … \ln(A)=(A-I)-\frac{(A-I)^2}2+\frac{(A-I)^3}3-\ldots ln(A)=(A−I)−2(A−I)2+3(A−I)3−…取其中的一阶项,可得: x ∧ = ln ( I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ ) ≈ I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ − I = − ( A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ \begin{aligned} x^{\wedge}& =\ln\left(I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right) \\ &\approx I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge-I \\ &=-\left(Ad(T_j^{-1})\delta\xi_i\right)^{\wedge}+\left(Ad(T_j^{-1})\delta\xi_j\right)^{\wedge} \end{aligned} x∧=ln(I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧)≈I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧−I=−(Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧
e ^ i j = ln ( T i j − 1 T i − 1 T j [ I + ( − A d ( T j − 1 ) δ ξ i ) ∧ + ( A d ( T j − 1 ) δ ξ j ) ∧ ] ) ∨ = ln ( exp ( e i j ∧ ) exp ( x ∧ ) ) ∨ \begin{aligned} \hat{e}_{ij}& =\ln\left(T_{ij}^{-1}T_i^{-1}T_j\left[I+\left(-Ad(T_j^{-1})\delta\xi_i\right)^\wedge+\left(Ad(T_j^{-1})\delta\xi_j\right)^\wedge\right]\right)^\vee \\ &=\ln\left(\exp(e_{ij}^{\wedge})\exp(x^{\wedge})\right)^{\vee} \end{aligned} e^ij=ln(Tij−1Ti−1Tj[I+(−Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧])∨=ln(exp(eij∧)exp(x∧))∨因此根据BCH的右乘近似公式可得(x为小量): e ^ i j = ln ( exp ( e i j ∧ ) exp ( x ∧ ) ) ∨ = J r − 1 ( e i j ) x + e i j \hat{e}_{ij}=\ln\left(\exp(e_{ij}^{\wedge})\exp(x^{\wedge})\right)^{\vee}=\mathcal{J}_r^{-1}(e_{ij})x+e_{ij} e^ij=ln(exp(eij∧)exp(x∧))∨=Jr−1(eij)x+eij ≈ J r − 1 ( e i j ) ( − A d ( T j − 1 ) δ ξ i + A d ( T j − 1 ) δ ξ j ) + e i j = e i j + ( − J r − 1 ( e i j ) A d ( T j − 1 ) ) ⏟ ∂ e i j ∂ δ ξ i δ ξ i + J r − 1 ( e i j ) A d ( T j − 1 ) ⏟ ∂ e i j ∂ δ ξ j δ ξ j \begin{aligned} &\approx\mathcal{J}_r^{-1}(e_{ij})\left(-Ad(T_j^{-1})\delta\xi_i+Ad(T_j^{-1})\delta\xi_j\right)+e_{ij} \\ &=e_{ij}+\underbrace{\left(-\mathcal{J}_r^{-1}(e_{ij})Ad(T_j^{-1})\right)}_{\frac{\partial e_{ij}}{\partial\delta\xi_i}}\delta\xi_i+\underbrace{\mathcal{J}_r^{-1}(e_{ij})Ad(T_j^{-1})}_{\frac{\partial e_{ij}}{\partial\delta\xi_j}}\delta\xi_j \end{aligned} ≈Jr−1(eij)(−Ad(Tj−1)δξi+Ad(Tj−1)δξj)+eij=eij+∂δξi∂eij (−Jr−1(eij)Ad(Tj−1))δξi+∂δξj∂eij Jr−1(eij)Ad(Tj−1)δξj(其中,为方便计算, J r − 1 ( e i j ) ≈ I + 1 2 [ ϕ e ∧ ρ e ∧ 0 ϕ e ∧ ] \left.\mathcal{J}_r^{-1}(e_{ij})\approx I+\frac{1}{2}\left[\begin{array}{cc}\phi_e^\wedge&\rho_e^\wedge\\\mathbf{0}&\phi_e^\wedge\end{array}\right.\right] Jr−1(eij)≈I+21[ϕe∧0ρe∧ϕe∧]或者 ≈ I \approx I ≈I)
通过 ∂ e i j ∂ δ ξ i = 0 \frac{\partial e_{ij}}{\partial\delta\xi_i}=0 ∂δξi∂eij=0 和 ∂ e i j ∂ δ ξ j = 0 \frac{\partial e_{ij}}{\partial\delta\xi_j}=0 ∂δξj∂eij=0 求得 δ ξ i \delta\xi_{i} δξi和 δ ξ j \delta\xi_{j} δξj不断迭代 ξ i \xi_{i} ξi 和 ξ j \xi_{j} ξj。求得目标函数 min 1 2 ∑ i , j ∈ E e i j T Σ i j − 1 e i j \min\frac12\sum_{i,j\in\mathcal{E}}e_{ij}^T\Sigma_{ij}^{-1}e_{ij} min21∑i,j∈EeijTΣij−1eij的最小值。
四、实践g2o_viewer报错解决方案
问题1:
g2o_viewer: command not found
原因:
之前编译g2o库的时候因为少装了部分依赖所以没有编译出 g2o_viewer的可执行文件
解决方案:
补充下述依赖
sudo apt-get install libsuitesparse-dev qtdeclarative5-dev qt5-qmake
sudo apt-get install libqglviewer-dev-qt5
进入g2o的build文件夹下
cmake ..
make
sudo make install
问题2:
g2o_viewer: error while loading shared libraries: libg2o_viewer.so: cannot o
解决方案:
sudo ldconfig
(sudo ldconfig命令的作用是确保新安装的动态链接库能够被系统正确识别和共享)
相关文章:

视觉SLAM学习打卡【10】-后端·滑动窗口法位姿图
本节是对上一节BA的进一步简化,旨在提高优化实时性.难点在于位姿图部分的雅可比矩阵求解(涉及李代数扰动模型求导),书中的相关推导存在跳步(可能数学功底强的人认为过渡的理所当然),笔者参考了知…...

【动态规划 区间dp 位运算】100259. 划分数组得到最小的值之和
本文涉及知识点 动态规划 区间dp 位运算 LeetCode100259. 划分数组得到最小的值之和 给你两个数组 nums 和 andValues,长度分别为 n 和 m。 数组的 值 等于该数组的 最后一个 元素。 你需要将 nums 划分为 m 个 不相交的连续 子数组,对于第 ith 个子数…...
CSS核心样式-02-盒模型属性及扩展应用
目录 三、盒模型属性 常见盒模型区域 盒模型图 盒模型五大属性 1. 宽度 width 2. 高度 height 3. 内边距 padding 四值法 三值法 二值法 单值法 案例 4. 边框 border 按照属性值的类型划分为三个单一属性 ①线宽 border-width ②线型 border-style ③边框颜色 bo…...
在 Google Cloud 上轻松部署开放大语言模型
今天,“在 Google Cloud 上部署”功能正式上线! 这是 Hugging Face Hub 上的一个新功能,让开发者可以轻松地将数千个基础模型使用 Vertex AI 或 Google Kubernetes Engine (GKE) 部署到 Google Cloud。 Model Garden (模型库) 是 Google Clou…...

005Node.js模块URL的使用
引入 URL 模块 要使用 URL 模块,首先需要在代码中引入它。可以使用以下代码将 URL 模块导入到你的脚本中: const url require(url);实例代码 const urlrequire(url); var apihttp://www.baidu.com?nameshixiaobin&age20; console.log(url.parse(…...

美团笔试复盘
昨天做了美团的笔试,现在复盘一下。 1、将数组按照绝对值大小排序 有道算法题解决思路需要将数组按照绝对值大小进行排序,我使用的是sort方法Comparator比较器实现的,这里记录一下: public static void main(String[] args) {In…...
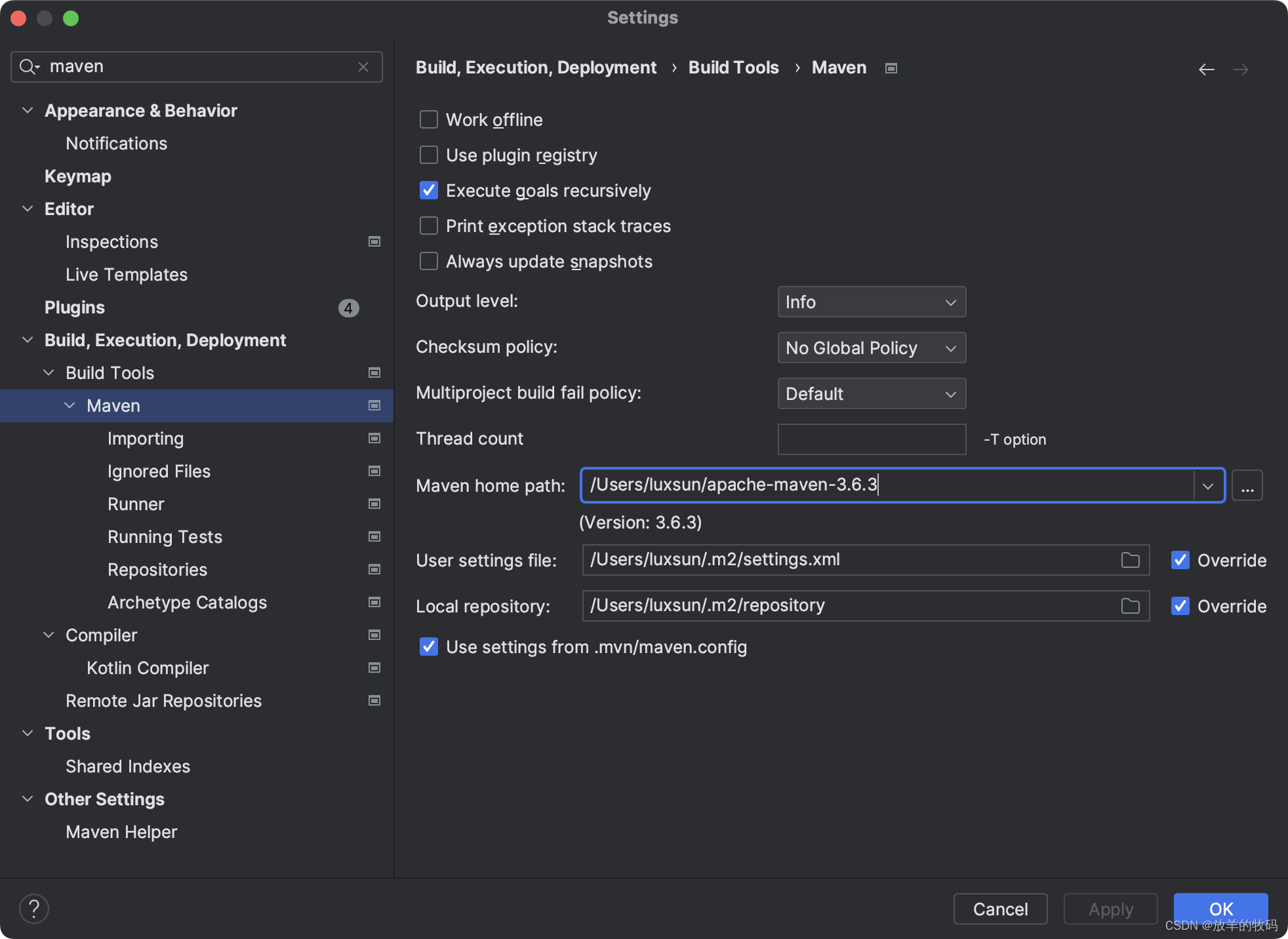
IntelliJ IDEA - Since Maven 3.8.1 http repositories are blocked
问题描述 新下载的 IDEA 在构建项目时,在下载引用的包时出现 “Since Maven 3.8.1 http repositories are blocked” 的问题。 原因分析 从 Maven 3.8.1 开始,不再支持 http 的包了。由于现在对网络安全的日益重视,都在向 https 转变&#…...
流程)
Django的APP应用更名(重命名)流程
将Django中的一个现有APP更名是一个需要谨慎操作的过程,因为它涉及到多个文件和配置的更新。下面是详细的步骤和一些补充细节,帮助你更顺利地完成APP重命名: 1. 修改APP名称及相关引用 更改APP目录名称: 首先,重命名…...

ChatGLM3-6B大语言模型离线执行
ChatGLM3-6B大语言模型离线执行 模型准备 一般而言,模型和模型参数可以通过如下三个模型源进行相应的下载: HuggingFace | ModelScope | WiseModel 本实例中,使用的是HuggingFace的源下载,相应的地址如下: HuggingFa…...
了解大语言模型的参数高效微调(Parameter-Effcient Fine-Tuning)
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 大语言模型在众多应用领域实现了突破性的进步,显著提升了各种任务的完成度。然而,其庞大的规模也带来了高昂的计算成本。这些模型往往包含数十亿甚至上千亿参数,需要…...

2024.4.14力扣每日一题——设计哈希集合
2024.4.14 题目来源我的题解方法一 链表数组 题目来源 力扣每日一题;题序:705 我的题解 方法一 链表数组 由于给定限制次数为10000,所以构造一个长度为10001的链表数组。对于add操作先看数组对应的位置是否为null或者为空,若是…...

SQL explain 显示子查询A类型为ALL怎么优化
当 SQL EXPLAIN 显示子查询 A 的类型为 ALL 时,这意味着数据库系统正在执行全表扫描,而不是使用索引来执行子查询。全表扫描可能会导致性能下降,特别是在大型表上。 为了优化这种情况,您可以考虑以下几点: 1. **索引…...

网络协议学习——IP协议
IP(Internet Protocol,互联网协议)是网络中最基本的协议之一,负责在互联网中进行数据包的传输。下面是对IP协议的详细讲解: IP协议的作用 IP协议是在网络层(第三层)上工作的协议,它的…...
—— 基础知识和功能介绍)
MATLAB初学者入门(1)—— 基础知识和功能介绍
MATLAB(Matrix Laboratory)是一种用于数值计算、可视化以及编程的高性能语言环境。它广泛应用于工程、科学研究和教育等领域。以下是对MATLAB基础知识和编程技巧的系统性讲解,分为几个主要部分: 1. 基础操作 变量和表达式 在MAT…...

React Css 四种引入方式
React CSS 内联样式 优点 样式之间不会有冲突可以动态获取组件中state的值 缺点 要使用驼峰标识部分样式没有很友好的提示如果大量去写内敛样式 容易造成代码混乱伪类和伪元素无法编写 class HighCom extends PureComponent {constructor(props) {super(props)this.state…...

题目:输入3个数a,b,c,按大小顺序输出。
题目:输入3个数a,b,c,按大小顺序输出。 There is no nutrition in the blog content. After reading it, you will not only suffer from malnutrition, but also impotence. The blog content is all parallel goods. Those who are worried abou…...
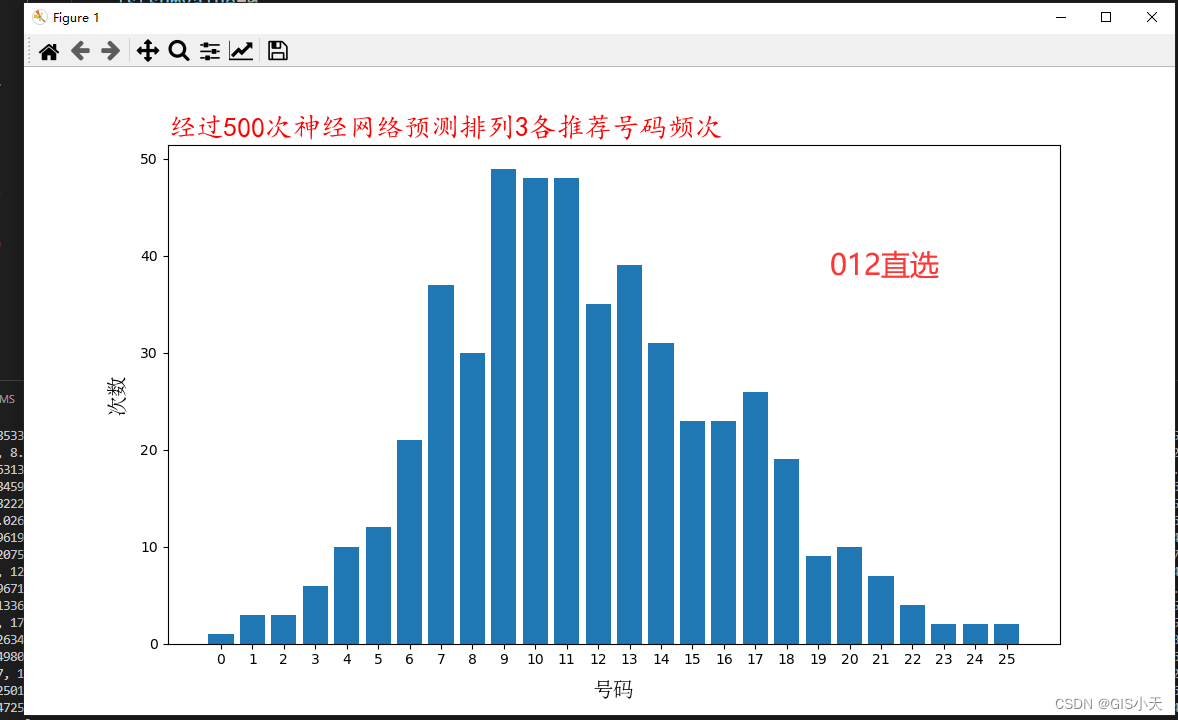
AI预测体彩排3第3弹【2024年4月14日预测--第1套算法开始计算第3次测试】
今天咱们继续测试第1套算法和模型,今天是第3次测试,目前的测试只是为了记录和验证,不建议大家盲目跟买。我的目标仍旧是10次命中3-4次!~废话不多说了,直接上结果! 2024年4月14日排3的七码预测结果如下 第一套&…...

Android 在xml 布局中如何嵌套 Jetpack Compose
最近在项目开发的过程中需要用到 Jetpack Compose,之前没有接触过Compose,所以项目一直没有用到Compose。通过查看官网发现Compose上手比较快,但是准备比较复杂的布局要转换成Compose 不是一件容易的事情。那有没有可能只是对成熟的项目中的x…...

Spring Boot统一功能处理(一)
本篇主要介绍Spring Boot的统一功能处理中的拦截器。 目录 一、拦截器的基本使用 二、拦截器实操 三、浅尝源码 初始化DispatcherServerlet 处理请求(doDispatch) 四、适配器模式 一、拦截器的基本使用 在一般的学校或者社区门口,通常会安排几个…...

我与C++的爱恋:类与对象(二)
🔥个人主页:guoguoqiang. 🔥专栏:我与C的爱恋 本篇着重介绍构造函数和析构函数,剩余内容在下篇解答。 一、类的默认成员函数 如果一个类中什么成员都没有,简称为空类。 任何类在什么都不写时…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
