在windows系统中【.gz.tar】和【.whl】文件分别应该怎么下载到conda的某个虚拟环境中
在 Windows 系统中,你可以按照以下步骤将 .gz.tar 和 .whl 文件下载到 Conda 的某个虚拟环境中:
-
激活虚拟环境:打开 Anaconda Prompt 或者命令行窗口,使用以下命令激活你想要安装文件的虚拟环境:
conda activate <虚拟环境名称> -
下载文件:使用浏览器或者命令行工具下载
.gz.tar或.whl文件。你可以在浏览器中直接访问文件的 URL 进行下载,或者使用命令行工具如curl或wget:- 对于
.gz.tar文件:
或者wget <文件URL>curl -O <文件URL> - 对于
.whl文件:curl -O <文件URL>
- 对于
-
安装文件:下载完成后,使用相应的命令安装文件。对于
.gz.tar文件,你需要解压缩并安装。在命令行中切换到下载文件的目录,然后执行以下操作:tar -zxvf <文件名>.gz.tar cd <解压后的目录> python setup.py install对于
.whl文件,可以直接使用以下命令安装:pip install <文件名>.whl -
验证安装:安装完成后,可以通过命令行工具验证文件是否成功安装到了虚拟环境中。例如,对于 Python 包,可以使用
pip list命令查看已安装的包列表。
请注意替换上述命令中的 <文件URL> 和 <文件名> 为实际文件的 URL 和名称。
相关文章:

在windows系统中【.gz.tar】和【.whl】文件分别应该怎么下载到conda的某个虚拟环境中
在 Windows 系统中,你可以按照以下步骤将 .gz.tar 和 .whl 文件下载到 Conda 的某个虚拟环境中: 激活虚拟环境:打开 Anaconda Prompt 或者命令行窗口,使用以下命令激活你想要安装文件的虚拟环境: conda activate <虚…...

Rust - 数据类型
Rust 是静态编译语言,在编译时必须知道所有变量的类型。 基于使用的值,编译器通常能推断出它的具体类型,但如果可能的类型比较多,例如把String转换为整数的parse方法,就必须添加类型的标注,否则编译会报错…...
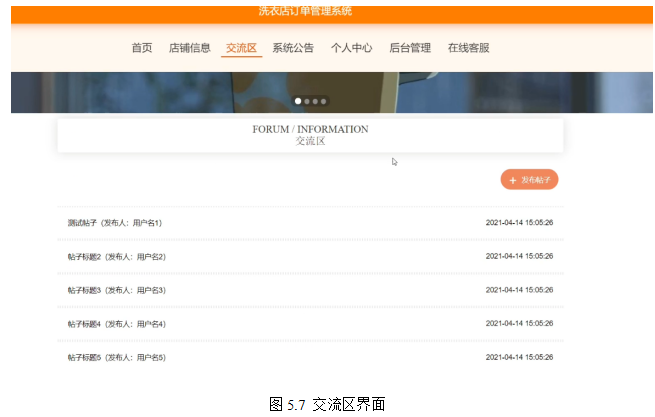
基于springboot实现洗衣店订单管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现洗衣店订单管理系统演示 摘要 随着信息互联网信息的飞速发展,无纸化作业变成了一种趋势,针对这个问题开发一个专门适应洗衣店业务新的交流形式的网站。本文介绍了洗衣店订单管理系统的开发全过程。通过分析企业对于洗衣店订单管理系统…...
)
Java基础知识总结(53)
(1)集合框架概述 Java集合大致分为List、Set、Map和Queue Collection是一个顶级接口,其子接口有,List、Set、Queue List:有序(存放和取出顺序是一致的)、有索引、可重复 Set:无序、无索引、不可重复 &…...

196算法之谜在 JSP 中使用内置对象 request 获取 form 表单的文本框 text 提交的数据。
(1)编写 inputNumber . jsp ,该页面提供一个 form 表单,该 form 表单提供一个文本框 text ,用于用户输入一个正整数,用户在 form 表单中输入的数字,单击 submit 提交键将正整数提交给 huiwenNumber . jsp 页…...

初识责任链模式--一起学习吧之数据库
一、定义 责任链模式是一种对象行为型模式,用于处理请求发送者和多个请求处理者之间的耦合问题。在这种模式中,请求的处理者通过前一对象记住其下一个对象的引用而连成一条链。当有请求发生时,请求会沿着这条链传递,直到有对象处…...
解决Xshell登录云服务器的免密码和云服务器生成子用户问题
Xshell登录云服务器的免密码问题 前言一、Xshell登录云服务器的免密码操作实践 二、centos创建用户创建用户实操删除用户更改用户密码直接删除子用户 前言 Xshell登录云服务器免密码问题的解决方案通常涉及使用SSH密钥对。用户生成一对密钥(公钥和私钥)…...

webRtc生产环境实用方法
最近做了几个项目发现多个项目反反复复会出现几个高频的需求, 都依赖于获取系统采集设备和指定设备id获取媒体流;为了不在反复书写总结2个公用方法; 检索当前系统所有可用设备 /*** 检索当前系统所有可用设备* returns {* audioInputOption…...

Java String、StringBuffer
构造方法 通过字符数组构造,结果abc 通过字节数组构造,结果abc //把字符串转化为字节数组 当前代码编译环境为UTF-8,出现异常时,直接抛出异常即可。mainthrows UnsupportedEncodingException 编译环境为UTF-8,但是运用gb2312这个…...
)
LangChain调用tool集的原理剖析(包懂)
一、需求背景 在聊天场景中,针对用户的问题我们希望把问题逐一分解,每一步用一个工具得到分步答案,然后根据这个中间答案继续思考,再使用下一个工具得到另一个分步答案,直到最终得到想要的结果。 这个场景非常匹配la…...

如何正确使用数字化仪前端信号调理?(一)
一、前言 板卡式的数字转换器和类似测量仪器,比如图1所示的德思特TS-M4i系列,都需要为各种各样的特性信号与内部模数转换器(ADC)的固定输入范围做匹配。 图1:德思特TS-M4i系列高速数字化仪,包括2或4通道版…...
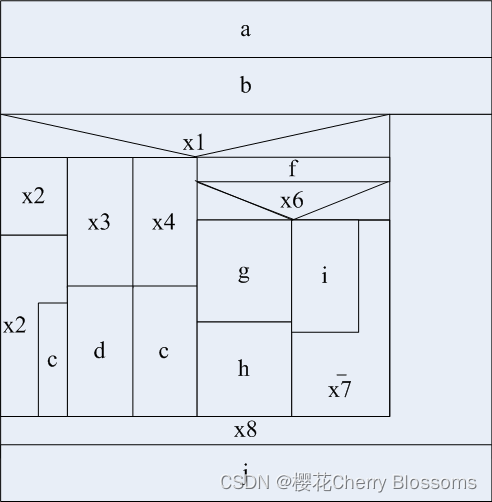
实验5 流程图和盒图ns图
一、实验目的 通过绘制流程图和盒图,熟练掌握流程图和盒图的基本原理。 能对简单问题进行流程图和盒图的分析,独立地完成流程图和盒图设计。 二、实验项目内容(实验题目) 1、用Microsoft Visio绘制下列程序的程序流程图。 若…...
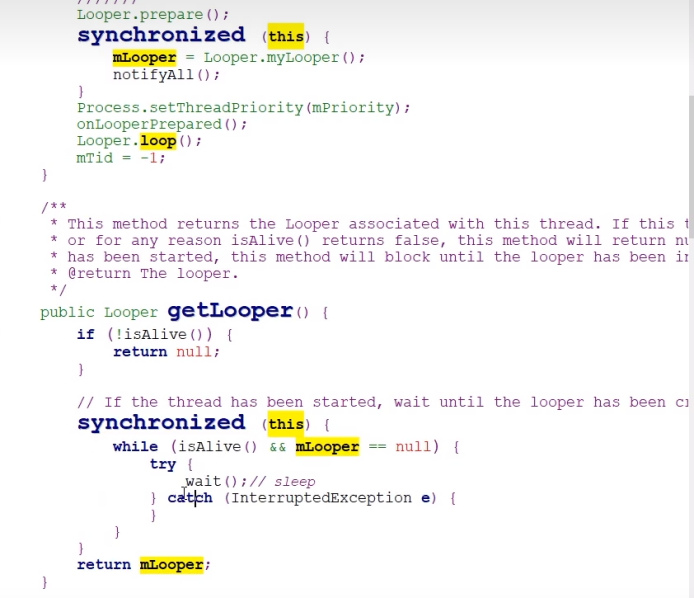
[Java、Android面试]_18_详解Handler机制 常见handler面试题(非常重要,非常高频!!)
本人今年参加了很多面试,也有幸拿到了一些大厂的offer,整理了众多面试资料,后续还会分享众多面试资料。 整理成了面试系列,由于时间有限,每天整理一点,后续会陆续分享出来,感兴趣的朋友可关注收…...
国内开通gpt会员方法
ChatGPT镜像 今天在知乎看到一个问题:“平民不参与内测的话没有账号还有机会使用ChatGPT吗?” 从去年GPT大火到现在,关于GPT的消息铺天盖地,真要有心想要去用,途径很多,别的不说,国内GPT的镜像…...

使用 Meltano 将数据从 Snowflake 导入到 Elasticsearch:开发者之旅
作者:来自 Elastic Dmitrii Burlutskii 在 Elastic 的搜索团队中,我们一直在探索不同的 ETL 工具以及如何利用它们将数据传输到 Elasticsearch,并在传输的数据上实现 AI 助力搜索。今天,我想与大家分享我们与 Meltano 生态系统以及…...

第24次修改了可删除可持久保存的前端html备忘录:文本编辑框不再隐藏,又增加了哔哩哔哩搜索和必应搜索
第24次修改了可删除可持久保存的前端html备忘录:文本编辑框不再隐藏,又增加了哔哩哔哩搜索和必应搜索. <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta name"viewport" content"…...

二极管分类及用途
二极管分类及用途 通用开关二极管 特点:电流小,工作频率高 选型依据:正向电流、正向压降、功耗,反向最大电压,反向恢复时间,封装等 类型:BAS316 ; IN4148WS 应用电路: 说明:应用…...

文献阅读:Viv:在 web 上多尺度可视化高分辨率多重生物成像数据
文献介绍 「文献题目」 Viv: multiscale visualization of high-resolution multiplexed bioimaging data on the web 「研究团队」 Nils Gehlenborg(美国哈佛医学院) 「发表时间」 2022-05-11 「发表期刊」 Nature Methods 「影响因子」 47.9 「DOI…...

SpringBoot整合Logback日志框架
Logback 是一个灵活而高效的日志框架,它是由 Ceki Glc 开发的,也是 Log4j 的创建者之一。Logback 旨在成为 Log4j 的替代品,并提供了一系列强大的功能和性能改进。 以下是 Logback 的一些主要特点和功能: 模块化结构:…...

知识图谱与人工智能:携手共进
知识图谱与人工智能:携手共进 一、引言:知识图谱与人工智能的融合 在这个数据驱动的时代,知识图谱与人工智能(AI)之间的融合不仅是技术发展的必然趋势,也是推动各行各业创新的关键。知识图谱,作…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
