【stata】求滚动波动情况
0.计算对象
计算 t t t、 t + 1 t+1 t+1、 t + 2 t+2 t+2 这三起滚动波动情况
V o l i , t = l n ( ∑ n = t n = t + 2 ( g n − g ˉ ) 2 3 ) Vol_{i,t} = ln(\sqrt{\frac{\sum_{n=t}^{n=t+2}(g_{n}-\bar{g})^2}{3}}) Voli,t=ln(3∑n=tn=t+2(gn−gˉ)2)
e . g e.g e.g: 假设 2008-2010的value分别为【6.264004 】、 【11.11958】 、 【18.7657】
三年均值 g ˉ \bar{g} gˉ等于【12.049761】
此处数据与stata模拟数据一致,便于对比手动计算结果和代码计算结果是否一致,
进而证明代码的有效性。
. di (6.264004 + 11.11958 + 18.7657) / 3
12.049761
V o l i , 2008 = l n ( ∑ n = 2008 n = 2010 ( g n − g ˉ ) 2 3 ) Vol_{i,2008} = ln(\sqrt{\frac{\sum_{n=2008}^{n=2010}(g_{n}-\bar{g})^2}{3}}) Voli,2008=ln(3∑n=2008n=2010(gn−gˉ)2)
V o l i , 2008 = l n ( ( 6.26 − 12.05 ) 2 + ( 11.12 − 12.05 ) 2 + ( 18.77 − 12.05 ) 2 3 ) Vol_{i,2008} = ln(\sqrt{\frac{(6.26-12.05)^2 + (11.12-12.05)^2 + (18.77-12.05)^2 }{3}}) Voli,2008=ln(3(6.26−12.05)2+(11.12−12.05)2+(18.77−12.05)2)
V o l i , 2008 = l n ( 79.5474 3 ) Vol_{i,2008} = ln(\sqrt{\frac{79.5474 }{3}}) Voli,2008=ln(379.5474)
V o l i , 2008 = l n ( 26.5158 ) Vol_{i,2008} = ln(\sqrt{26.5158}) Voli,2008=ln(26.5158)
V o l i , 2008 = l n ( 5.1493495 ) Vol_{i,2008} = ln(5.1493495) Voli,2008=ln(5.1493495)
V o l i , 2008 = 1.63 Vol_{i,2008} = 1.63 Voli,2008=1.63
1.模拟数据
clear
set seed 123
set obs 10// ssc install egenmore,replace
egen id = repeat(),v(1/2)
sort id
egen year = repeat(),v(2008/2012)
gen value = uniform() * 20
replace year = year - 1 if id == 2list id year value运行结果
Number of observations (_N) was 0, now 10.(5 real changes made)+----------------------+| id year value ||----------------------|1. | 1 2008 6.264004 |2. | 1 2009 11.11958 |3. | 1 2010 18.7657 |4. | 1 2011 14.72644 |5. | 1 2012 3.848151 ||----------------------|6. | 2 2007 3.902801 |7. | 2 2008 19.0192 |8. | 2 2009 5.808908 |9. | 2 2010 16.38165 |10. | 2 2011 9.764193 |+----------------------+
2.根据unit id 拆分成多个dta
egen count = group(id)
su count,d
global dim = r(max)forv i = 1/$dim{preservekeep if count == `i'drop countsave temp`i'.dta,replace restore
}
3.对于每一个unit滚动求和
先定义滚动3年
然后求这3年内的value的平均 g ˉ \bar{g} gˉ
再用逐年的数值减去均值,
而后求平方项 / 3
最后取对数
forv id = 1/$dim{
use temp`id'.dta,replace
su year ,dglobal row_year = 3 // 三年滚动求和global range_low = r(min)
global range_high = r(max) - $row_year + 1forv i = $range_low/$range_high{local j = `i' + $row_year - 1gen cond_bin = (year >= `i' & year <= `j')egen m_`i' = mean(value) if cond_bin == 1ereplace m_`i' = mean(m_`i')gen rolling_`i' = (value - m_`i')^2 if cond_bin == 1ereplace rolling_`i' = total(rolling_`i') if cond_bin == 1replace rolling_`i' = ln(sqrt(rolling_`i' / $row_year))drop cond_bin
}
keep id rolling*
forv i = $range_low/$range_high{ereplace rolling_`i' = mean(rolling_`i')
}
duplicates drop id ,force
reshape long rolling_,i(id) j(year)
save rolling_`id'.dta,replace
}
4.合并/清除数据
use rolling_1.dta,replace
forv id = 2/$dim{append using rolling_`id'.dta
}
forv i = 1/$dim{erase temp`i'.dtaerase rolling_`i'.dta
}
save rolling.dta,replace
5.运行结果
use rolling.dta,clear
list id year roll in 1/6
结果对比:可以看到,id=1时,year=2008时,代码计算结果也为1.63,与手动计算结果一致,证明了代码的有效性
+----------------------+| id year rolling_ ||----------------------|1. | 1 2008 1.638221 |2. | 1 2009 1.138851 |3. | 1 2010 1.840516 |4. | 2 2007 1.905365 |5. | 2 2008 1.741902 |6. | 2 2009 1.472856 |+----------------------+
相关文章:

【stata】求滚动波动情况
0.计算对象 计算 t t t、 t 1 t1 t1、 t 2 t2 t2 这三起滚动波动情况 V o l i , t l n ( ∑ n t n t 2 ( g n − g ˉ ) 2 3 ) Vol_{i,t} ln(\sqrt{\frac{\sum_{nt}^{nt2}(g_{n}-\bar{g})^2}{3}}) Voli,tln(3∑ntnt2(gn−gˉ)2 ) e . g e.g e.g: 假设 200…...
The C programming language (second edition,KR) exercise(CHAPTER 2)
E x c e r c i s e 2 − 1 Excercise\quad 2-1 Excercise2−1:输出结果如图1和图2所示,这道练习题需要文章1和文章2的知识。 #include <stdio.h> #include <limits.h>float getFloat(char sign, unsigned char exp, unsigned mantissa); do…...

rust实现循环链表
作为一个计算机技术专家,针对你的问题,我将首先解释如何使用Rust语言实现循环链表,并提供相应的代码示例。然后,我将解释一个可能的报错问题及其解决方法。 循环链表的实现 在Rust中实现循环链表,首先需要定义链表节…...

2. Spring的创建和Bean的存取
经过前面的学习我们已经大体明白了 IOC 思想以及它的实现方式 DI ,本节要讲的是如何Spring框架实现实现DI。 本节目标: Spring(Core) 项目创建将对象存储到 Spring 中将对象(bean)从 Spring 中取出 1. 创建 Spring 项目 与开篇演示的 Spring Boot 项目不…...
策略模式【行为模式C++】
1.概述 策略模式是一种行为设计模式, 它能让你定义一系列算法, 并将每种算法分别放入独立的类中, 以使算法的对象能够相互替换。 策略模式通常应用于需要多种算法进行操作的场景,如排序、搜索、数据压缩等。在这些情况下&#x…...
)
php中session相关知识(目前了解部分)
#记录学习知识 一.ini_set() 在PHP中,ini_set() 函数用于在脚本运行时设置指定的配置选项的值。这些配置选项可以是PHP的核心设置,例如文件上传的最大大小、脚本的最大执行时间、错误报告级别等。使用 ini_set() 可以临时改变PHP.ini文件中的设置&am…...

从零实现诗词GPT大模型:GPT是怎么生成内容的?
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 再开始编写GPT之前,我们得对GPT是怎么生成内容的有一个大致的了解。目前的神经网络我们大多都可以看成是一个黑盒,即我们把数据输送给网络后,网络给我我们输出,我们可以不用关心这个黑盒里到底是怎么实现…...

8路HDMI+8路AV高清视频流媒体编码器JR-3218HD
产品简介: JR-3218HD高清音视频编码产品支持8路高清HDMI音视频采集功能,8路AV视频采集功能,8路3.5MM独独立音频接口采集功能。编码输出双码流H.264格式,音频MP3/AAC格式。编码码率可调,画面质量可控制。支持HTTP/RTSP…...

LangChain入门:14.LLMChain:最简单的链的使用
摘要 本文将介绍LangChain库中LLMChain工具的使用方法。LLMChain将提示模板、语言模型(LLM)和输出解析器整合在一起,形成一个连贯的处理链,简化了与语言模型的交互过程。我们将探讨LLMChain的技术特点、应用场景以及它解决的问题…...
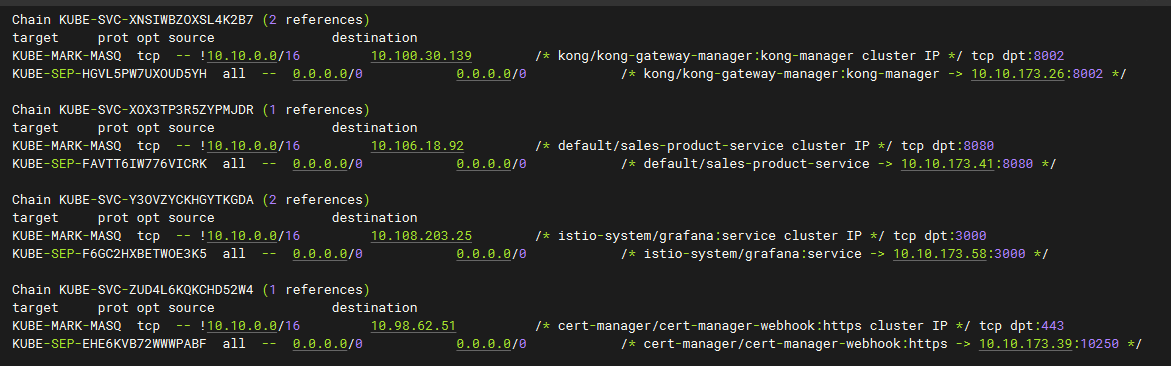
深入理解k8s kube-proxy
1、概述 我觉得只要大家知道kube-proxy是用来配置网络规则的而不是转发流量的,真正的流量由iptables/ipvs来转发就可以了。 网络是k8s的一个关键部分。理解k8s中网络组件如何工作可以帮助更好的设计和配置我们的应用。 kube-proxy就是K8s网络的核心组件。它把我们…...
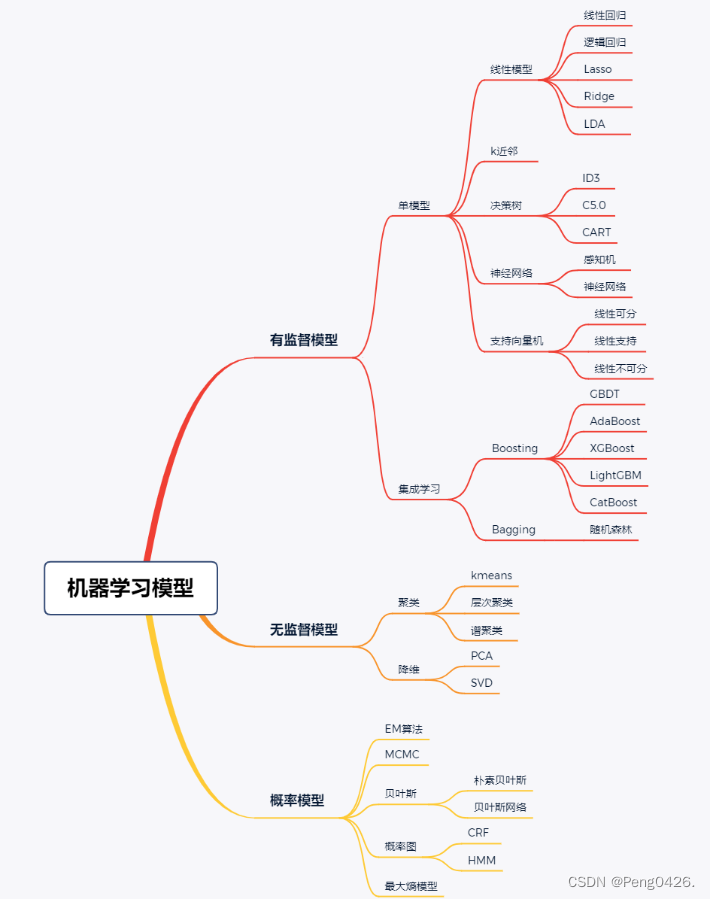
Spark-机器学习(1)什么是机器学习与MLlib算法库的认识
从这一系列开始,我会带着大家一起了解我们的机器学习,了解我们spark机器学习中的MLIib算法库,知道它大概的模型,熟悉并认识它。同时,本篇文章为个人spark免费专栏的系列文章,有兴趣的可以收藏关注一下&…...

java的正则表达式校验,包含了中国几乎所有运营商手机号码的校验格式
时间2024年4月14日22:25:00 代码 String PHONE_REGEX "^1([38][0-9]|4[579]|5[0-3,5-9]|6[6]|7[0135678]|9[89])\\d{8}$";解释 这个Java代码段定义了一个常量 PHONE_REGEX,它包含了一个正则表达式,用于匹配中国大陆的手机号码。下面是对这…...
C#简单工厂模式的实现
using System.Diagnostics.Metrics; using System.Runtime.InteropServices; using static 手写工厂模式.Program;namespace 手写工厂模式 {internal class Program{public interface eats {void eat();}//定义了一个接口public class rice : eats{public void eat() {Console.…...
)
.NET 设计模式—观察者模式(Observer Pattern)
简介 在.NET中,观察者模式是一种设计模式,它允许对象之间进行一对多的依赖关系。当一个对象的状态发生变化时,所有依赖于它的对象都会收到通知并自动更新。这种模式在事件驱动的设计中非常常见。 在.NET中实现观察者模式,通常涉…...
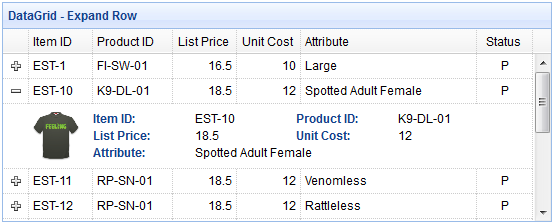
EasyUI Jquery 学习笔记 ——DataGrid(数据网格)与 Tree(树)详细版
1. DataGrid(数据网格)与 Tree(树) 1.1 Datagrid 数据网格 扩展自 $.fn.panel.defaults。通过 $.fn.datagrid.defaults 重写默认的 defaults。 数据网格(datagrid)以表格格式显示数据,并为选择、排序、分组和编辑数据提供了丰富的支持。数据网格(datagrid)的设计目…...

JAVA发票验真接口、票据ocr、数电票在线查验真伪
发票验真接口,,实时联网核验发票真伪,查验一致返回全票面信息,支持查验增值税发票管理系统开具的发票,支持批量核验发票,翔云发票查验送发票识别,助您摆脱手动输入繁琐,提升工作效率。 发票查验接口适用于银行、金融、代理记账等发票管理数量…...

el-date-picker调用回车事件
elementui的el-date-picker想要调用回车事件: <el-date-pickerv-model"state.date"type"date"value-format"YYYY-MM-DD HH:mm:ss"placeholder"选择日期"clearablekeydown.enter"handleDown"></el-date-…...
js学习总结
这里写目录标题 前情提要JavaScript书写位置1. 内部javaScript (不常用)2. 外部javaScript (常用)3.内联javaScript (常用) js中的输入和输出输出语法1. document.write()2. alert()3. console.log() 输入语法prompt() 前情提要 1. 在javaScript中的 分号 是可以省略的JavaScr…...
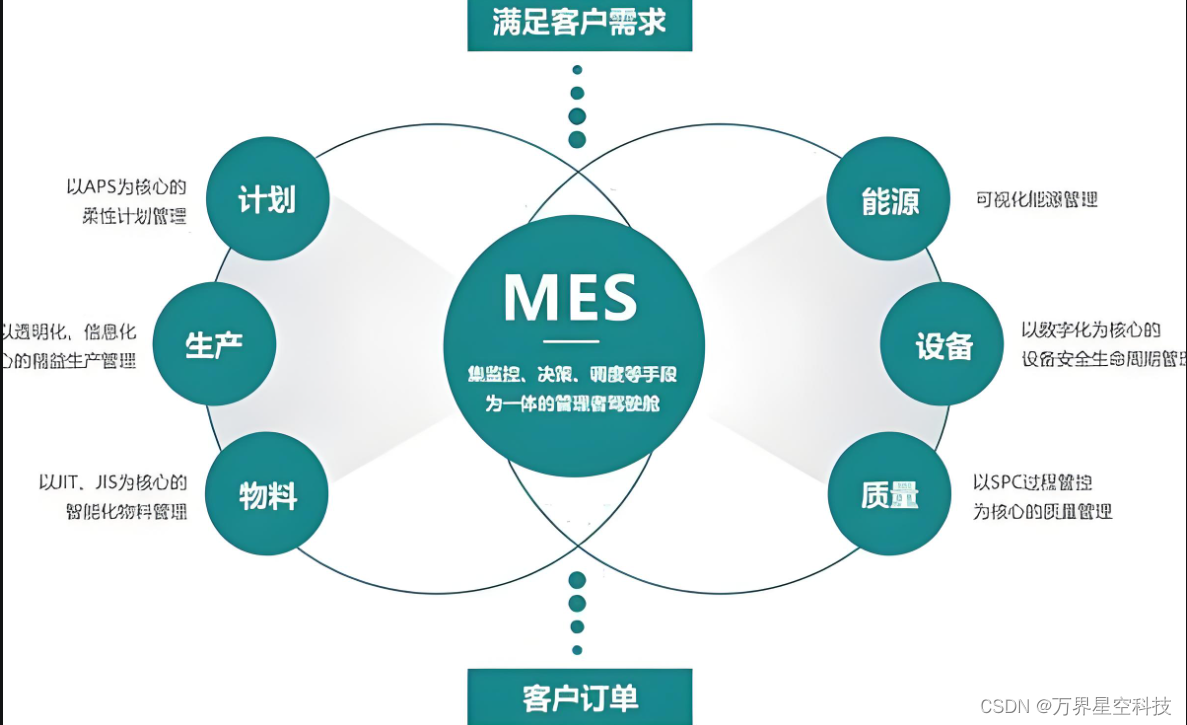
MES实施优势有哪些?MES制造执行系统的主要内容
各个行业之间也开始进入到了激烈的竞争当中,很多企业为了能够有效提升企业竞争力,都会通过提升自身实力的方式来提升竞争力。一些制造业也会在经营过程当中使用到MES系统,那么,mes系统的优势有哪些呢? 1、优化企业现场…...
ChatGPT 和 Elasticsearch:使用 Elastic 数据创建自定义 GPT
作者:Sandra Gonzales ChatGPT Plus 订阅者现在有机会创建他们自己的定制版 ChatGPT,称为 GPT,这替代了之前博客文章中讨论的插件。基于本系列的第一部分的基础 —— 我们深入探讨了在 Elastic Cloud 中设置 Elasticsearch 数据和创建向量嵌…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
