acwing算法提高之图论--最近公共祖先
目录
- 1 介绍
- 2 训练
1 介绍
本博客用来记录"对于有根图中,求最近公共祖先"的题目。
求解方法:
- 向上标记法。每次求两个结点的最近公共祖先的时间复杂度是
O(N)。由于时间复杂度较高,通常不用。 - 倍增法。
倍增法重要思路:预处理出两个数组fa[i][j]和depth[i]。其中fa[i][j]表示从i开始,向上走2^j步所能走到的结点。0<=j<=logn。depth[i]表示深度,为到根结点的距离再加上1。
哨兵:如果从i开始跳2^j步会跳过根结点,那么fa[i][j] = 0,depth[0] = 0。
倍增法重要步骤:
- 先将两个点跳到同一层。
- 让两个点同时往上跳,一直跳到它们的最近公共祖先的下一层。
倍增法的时间复杂度分析:预处理的时间复杂度为O(NlogN),查询的时间复杂度为O(logN)。
2 训练
题目1:1172祖孙询问
C++代码如下,
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>using namespace std;const int N = 40010;
int n, m;
int depth[N], fa[N][16];
int ancestor;
unordered_map<int, vector<int>> g;void bfs(int root) {memset(depth, 0x3f, sizeof depth);depth[0] = 0;depth[root] = 1; queue<int> q;q.push(root);while (!q.empty()) {int a = q.front();q.pop();for (auto b : g[a]) {if (depth[b] > depth[a] + 1) {depth[b] = depth[a] + 1;q.push(b);fa[b][0] = a;for (int k = 1; k <= 15; ++k) {fa[b][k] = fa[fa[b][k-1]][k-1];}}}}return;
}int lca(int a, int b) {//倍增法if (depth[a] < depth[b]) swap(a, b);for (int k = 15; k >= 0; --k) {if (depth[fa[a][k]] >= depth[b]) {a = fa[a][k];}}if (a == b) return a;for (int k = 15; k >= 0; --k) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];
}int main() {cin >> n;int a, b;for (int i = 0; i < n; ++i) {cin >> a >> b;if (b == -1) {ancestor = a;} else {g[a].emplace_back(b);g[b].emplace_back(a); }}cin >> m;vector<pair<int,int>> queries;for (int i = 0; i < m; ++i) {cin >> a >> b;queries.emplace_back(a,b);}//从根结点开始遍历bfs(ancestor);for (auto [a, b] : queries) {int x = lca(a, b);if (a == x) {puts("1");} else if (b == x) {puts("2");} else {puts("0");}}return 0;
}
题目2:1171距离
C++代码如下,
相关文章:

acwing算法提高之图论--最近公共祖先
目录 1 介绍2 训练 1 介绍 本博客用来记录"对于有根图中,求最近公共祖先"的题目。 求解方法: 向上标记法。每次求两个结点的最近公共祖先的时间复杂度是O(N)。由于时间复杂度较高,通常不用。倍增法。 倍增法重要思路࿱…...

C语言 函数——断言与防御式编程
目录 如何确定假设的真假? 断言 防御式编程(Defensive programming) 如何确定假设的真假? 程序中的假设 *某个特定点的某个表达式的值一定为真 *某个特定点的某个表达式的值一定位于某个区间等 问题:如何确定这些…...

【opencv】示例-travelsalesman.cpp 使用模拟退火算法求解旅行商问题
// 载入 OpenCV 的核心头文件 #include <opencv2/core.hpp> // 载入 OpenCV 的图像处理头文件 #include <opencv2/imgproc.hpp> // 载入 OpenCV 的高层GUI(图形用户界面)头文件 #include <opencv2/highgui.hpp> // 载入 OpenCV 的机器学习模块头文件 #includ…...

【linux深入剖析】深入理解软硬链接 | 动静态库的制作以及使用
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1.理解软硬链接1.1 操作观…...

xss常用标签和触发事件
无过滤情况 <script> <scirpt>alert("xss");</script> <img> 图片加载错误时触发 <img src"x" οnerrοralert(1)> <img src"1" οnerrοreval("alert(xss)")> 鼠标指针移动到元素时触发 <im…...

WPF中Binding的原理和应用
WPF中Binding的原理和应用 在WPF中,Binding机制是实现数据与界面的连接和同步的重要工具。了解Binding的原理和应用,对于开发人员来说是非常重要的。本文将详细介绍WPF中Binding的原理和应用,帮助读者更好地理解和运用这一强大的机制。 Bin…...

探索设计模式的魅力:深度挖掘响应式模式的潜力,从而精准优化AI与机器学习项目的运行效能,引领技术革新潮流
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,坚持默默的做事。 挖掘响应式模式,优化AI与机器学习项目性能,引领技术新潮流 ✨机器学习界的…...

《经典论文阅读2》基于随机游走的节点表示学习—Deepwalk算法
word2vec使用语言天生具备序列这一特性训练得到词语的向量表示。而在图结构上,则存在无法序列的难题,因为图结构它不具备序列特性,就无法得到图节点的表示。deepwalk 的作者提出:可以使用在图上随机游走的方式得到一串序列&#x…...

Java实现二叉树(下)
1.前言 http://t.csdnimg.cn/lO4S7 在前文我们已经简单的讲解了二叉树的基本概念,本文将讲解具体的实现 2.基本功能的实现 2.1获取树中节点个数 public int size(TreeNode root){if(rootnull){return 0;}int retsize(root.left)size(root.right)1;return ret;}p…...

Hello 算法10:搜索
https://www.hello-algo.com/chapter_searching/binary_search/ 二分查找法 给定一个长度为 n的数组 nums ,元素按从小到大的顺序排列,数组不包含重复元素。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素,则返回 -1 。 # 首…...

常见分类算法详解
在机器学习和数据科学的广阔领域中,分类算法是至关重要的一环。它广泛应用于各种场景,如垃圾邮件检测、图像识别、情感分析等。本文将深入剖析几种常见的分类算法,帮助读者理解其原理、优缺点以及应用场景。 一、K近邻算法(K-Nea…...

推送恶意软件的恶意 PowerShell 脚本看起来是人工智能编写的
威胁行为者正在使用 PowerShell 脚本,该脚本可能是在 OpenAI 的 ChatGPT、Google 的 Gemini 或 Microsoft 的 CoPilot 等人工智能系统的帮助下创建的。 攻击者在 3 月份的一次电子邮件活动中使用了该脚本,该活动针对德国的数十个组织来传播 Rhadamanthy…...

微服务之Consul 注册中心介绍以及搭建
一、微服务概述 1.1单体架构 单体架构(monolithic structure):顾名思义,整个项目中所有功能模块都在一个工程中开发;项目部署时需要对所有模块一起编译、打包;项目的架构设计、开发模式都非常简单。 当项…...

MES生产管理系统:私有云、公有云与本地化部署的比较分析
随着信息技术的迅猛发展,云计算作为一种新兴的技术服务模式,已经深入渗透到企业的日常运营中。在众多部署方式中,私有云、公有云和本地化部署是三种最为常见的选择。它们各自具有独特的特点和适用场景,并在不同程度上影响着企业的…...

【core analyzer】core analyzer的介绍和安装详情
目录 🌞1. core和core analyzer的基本概念 🌼1.1 coredump文件 🌼1.2 core analyzer 🌞2. core analyzer的安装详细过程 🌼2.1 方式一 简单但不推荐 🌼2.2 方式二 推荐 🌻2.2.1 安装遇到…...

个人练习之-jenkins
虚拟机环境搭建(买不起服务器 like me) 重点: 0 虚拟机防火墙关闭 systemctl stop firewalld.service systemctl disable firewalld.service 1 (centos7.6)网络配置 (vmware 编辑 -> 虚拟网络编辑器 -> 选择NAT模式 ->NAT设置查看网关) vim /etc/sysconfig/network-sc…...
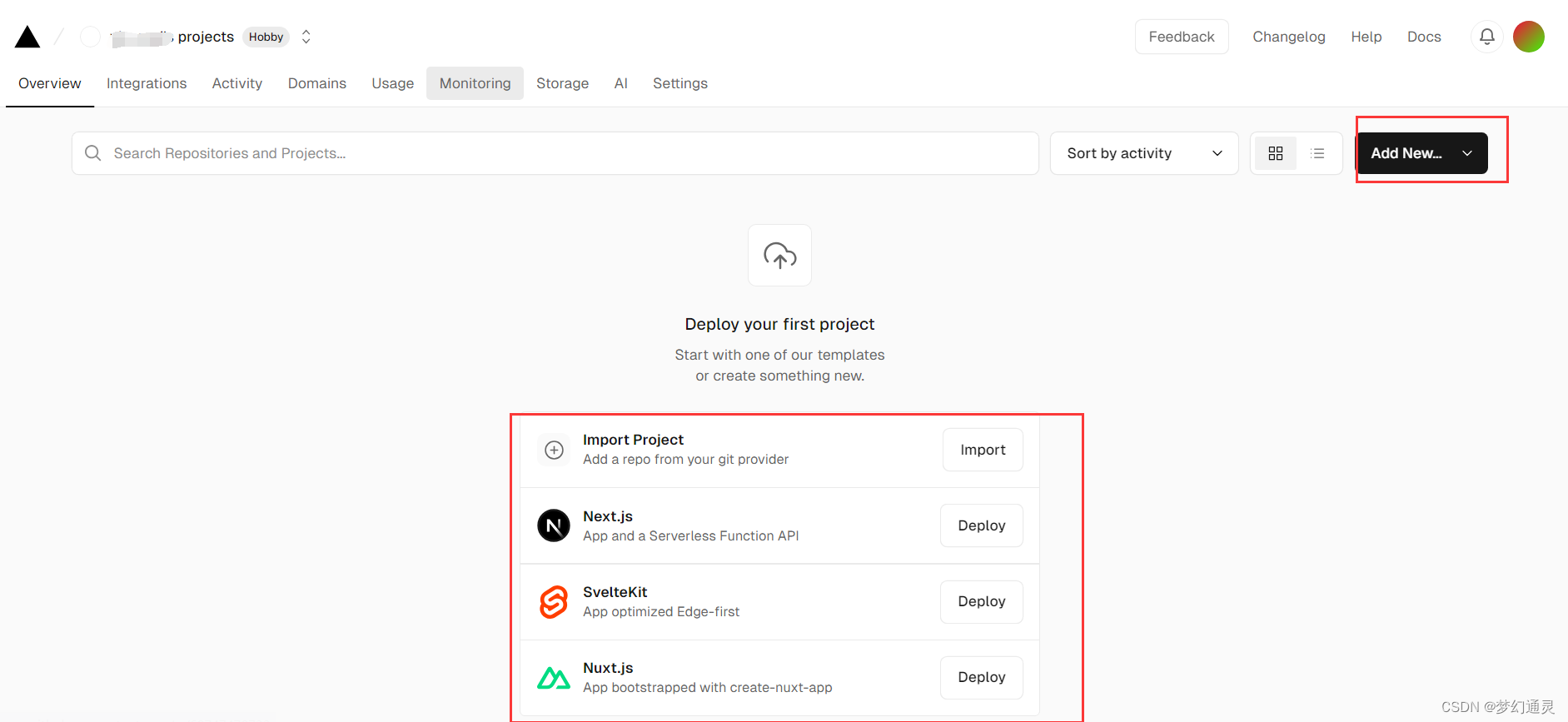
初探vercel托管项目
文章目录 第一步、注册与登录第二步、本地部署 在个人网站部署的助手vercel,支持 Github部署,只需简单操作,即可发布,方便快捷! 第一步、注册与登录 进入vercel【官网】,在右上角 login on,可登…...
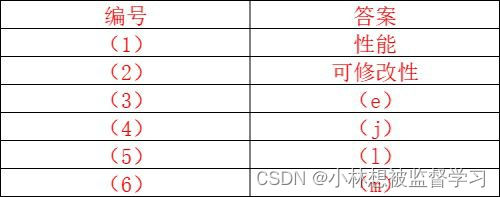
软考 - 系统架构设计师 - 质量属性例题 (2)
问题1: 、 问题 2: 系统架构风险:指架构设计中 ,潜在的,存在问题的架构决策所带来的隐患。 敏感点:指为了实现某个质量属性,一个或多个构件所具有的特性 权衡点:指影响多个质量属性…...

基于Python豆瓣电影数据可视化分析系统的设计与实现
大数据可视化项目——基于Python豆瓣电影数据可视化分析系统的设计与实现 2024最新项目 项目介绍 本项目旨在通过对豆瓣电影数据进行综合分析与可视化展示,构建一个基于Python的大数据可视化系统。通过数据爬取收集、清洗、分析豆瓣电影数据,我们提供了…...
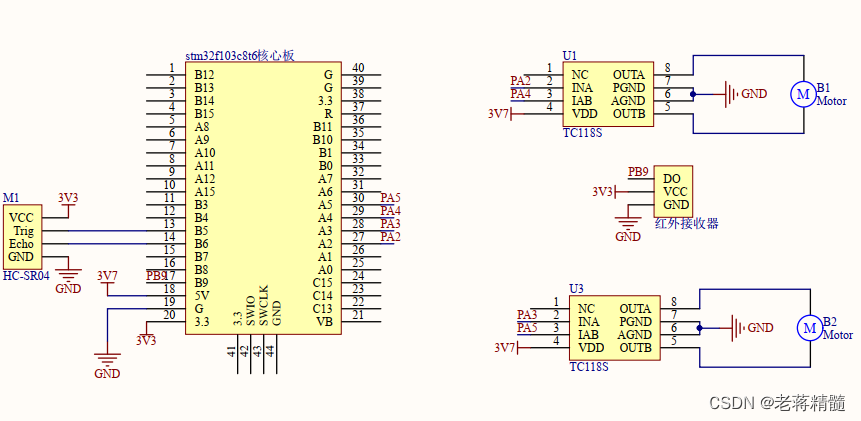
【已开源】基于stm32f103的爬墙小车
基于stm32f103的遥控器无线控制爬墙小车,实现功能为可平衡在竖直墙面上,并进行移动和转向,具有超声波防撞功能。 直接上: 演示视频如:哔哩哔哩】 https://b23.tv/BzVTymO 项目说明: 在这个项目中&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
