【机器学习300问】68、随机初始化神经网络权重的好处?
一、固定的初始化神经网络权重可能带来的问题
在训练神经网络的时候,初始化权重如果全部设置为0或某个过大值/过小值。会导致一些问题:
- 对称权重问题:全为0的初始化权重会导致神经网络在前向传播时接收到的信号输入相同。每个神经网络节点中的公式都是一样的,这种对称性会导致所有节点的输出完全一致,故而无法实现特征的多样性和区分度。这样一来一群节点和一个节点没什么区别。
- 梯度消失/爆炸:初始化权重过大或过小,可能会导致训练初期的梯度更新剧烈,引发梯度爆炸;反之,若权重过小,梯度则可能在反向传播过程中逐渐减小至接近于0,造成梯度消失。这两种情况都会严重影响网络的学习能力。
二、随机初始化神经网络权重的好处
(1)打破对称性
初始化神经网络的权重很像是给一个舞台剧的导演在剧开始前分配角色。如果所有角色一开始都是一样的,那么剧情将无法展开,因为每个演员都会做出完全相同的表演。相似地,如果我们给所有的神经网络权重相同的起始值,神经元将无法学习到不同的特征,因为在每次迭代中,每个神经元都会以相同的方式更新。这种现象称为对称权重问题。
随机初始化权重就像是为每个角色随机分配一种性格和背景。这虽然可能会有一定的混乱,但也为剧情发展提供了多样性和丰富性,每个演员能够为剧情提供独特的贡献。同样,在神经网络中,随机初始化权重能够打破权重的对称性,确保每个神经元可以学习到不同的特征。
随机初始化打破了这种对称性,每个神经元将以不同的初始权重开始训练,使得每个神经元从一开始就有独特的“视角”来处理输入数据,从而促进网络学习到更丰富的特征表示。
(2)避免梯度消失/爆炸
就如同为一辆赛车精心调整引擎转速,既不过热也不熄火,以确保其能在赛道上稳健加速。
随机初始化有助于分散权重的大小,使其既不太大也不太小,有利于保持梯度在合理的范围内波动,确保训练过程的稳定性。一般在使用Sigmoid激活函数和Tanh激活函数的神经网络中,通常设置成0.01。
(3)促进模型收敛
就像在广阔的森林中随机放置多个起点,让多个猎人同时出发寻找最优路线,比所有人都从同一个地方出发更容易快速找到通往猎物的最佳路径。
随机初始化为神经网络提供了广泛的搜索空间,使得模型在训练初期就能探索多种潜在的解决方案。随着训练的进行,模型通过反向传播和优化算法逐步调整这些初始权重,最终收敛到一个有效拟合训练数据的局部极小点。
相关文章:

【机器学习300问】68、随机初始化神经网络权重的好处?
一、固定的初始化神经网络权重可能带来的问题 在训练神经网络的时候,初始化权重如果全部设置为0或某个过大值/过小值。会导致一些问题: 对称权重问题:全为0的初始化权重会导致神经网络在前向传播时接收到的信号输入相同。每个神经网络节点中…...
数据结构与算法——20.B-树
这篇文章我们来讲解一下数据结构中非常重要的B-树。 目录 1.B树的相关介绍 1.1、B树的介绍 1.2、B树的特点 2.B树的节点类 3.小结 1.B树的相关介绍 1.1、B树的介绍 在介绍B树之前,我们回顾一下我们学的树。 首先是二叉树,这个不用多说ÿ…...
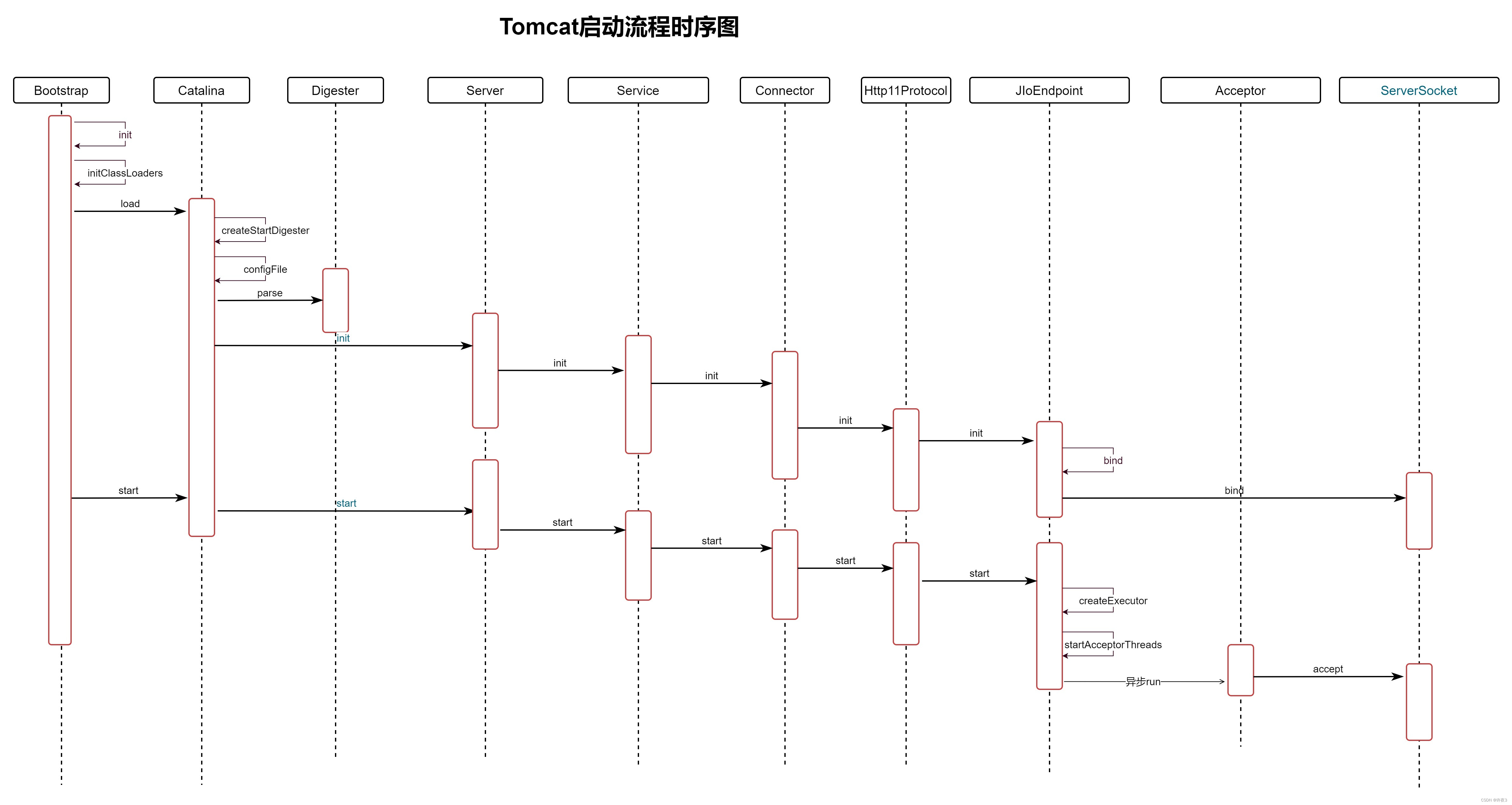
Tomcat源码解析——Tomcat的启动流程
一、启动脚本 当我们在服务启动Tomcat时,都是通过执行startup.sh脚本启动。 在Tomcat的启动脚本startup.sh中,最终会去执行catalina.sh脚本,传递的参数是start。 在catalina.sh脚本中,前面是环境判断和初始化参数,最终…...
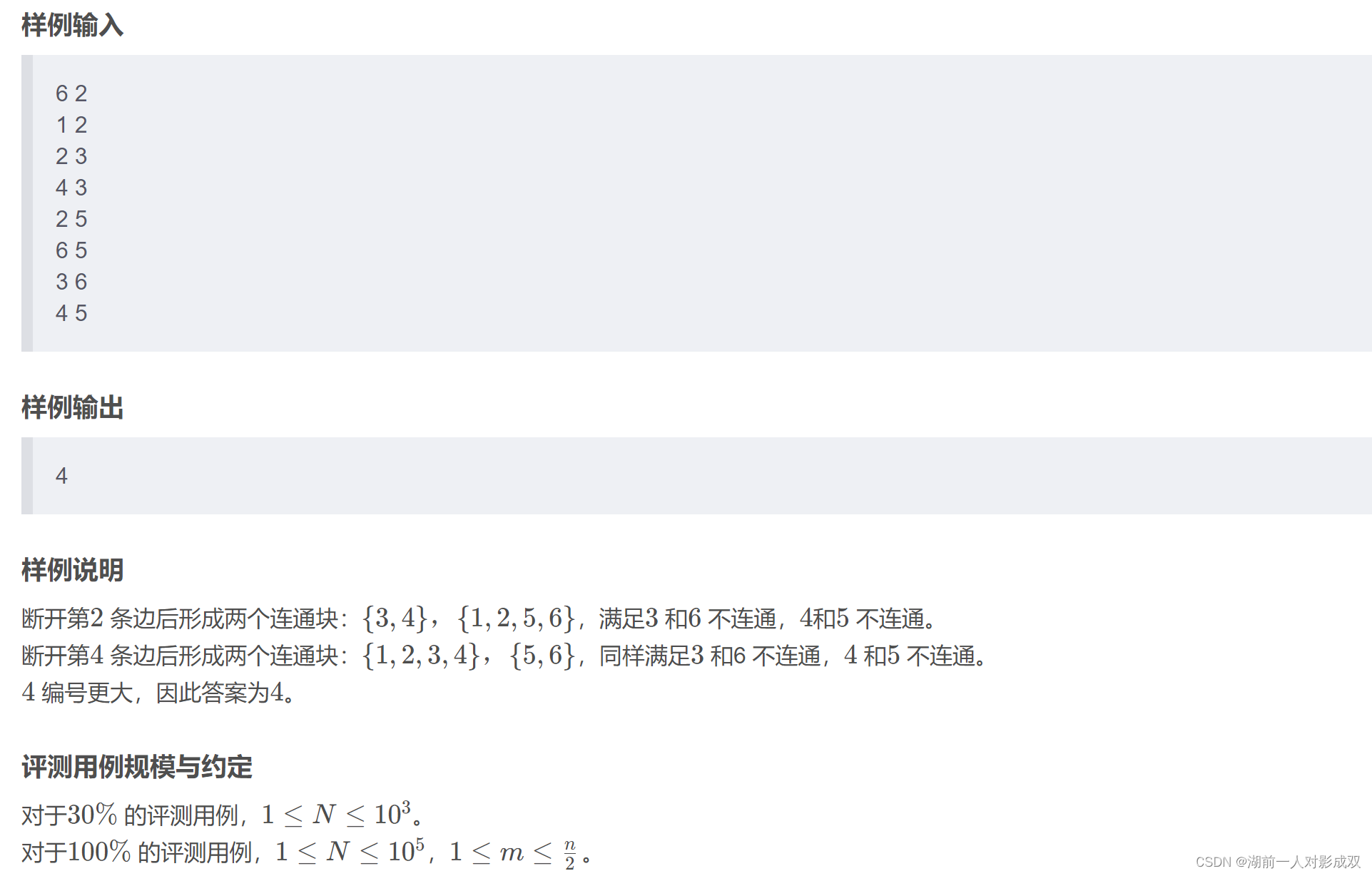
蓝桥杯真题演练:2023B组c/c++
日期统计 小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的范围之内。 数组中的元素从左至右如下所示: 5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 …...
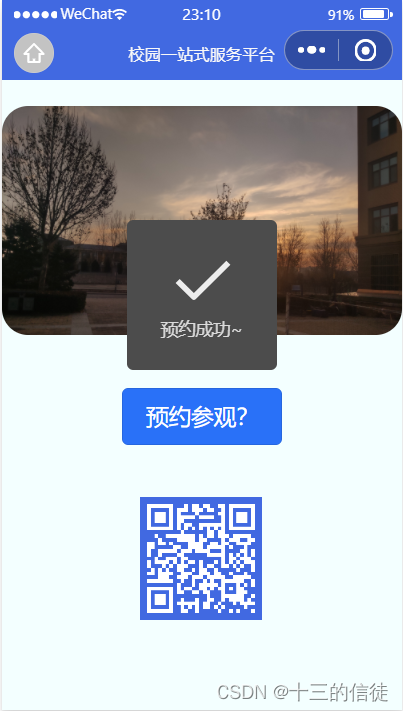
微信小程序实现预约生成二维码
业务需求:点击预约按钮即可生成二维码凭码入校参观~ 一.创建页面 如下是博主自己写的wxml: <swiper indicator-dots indicator-color"white" indicator-active-color"blue" autoplay interval"2000" circular > &…...

专业140+总分410+北京理工大学826信号处理导论考研经验北理工电子信息通信工程,真题,参考书,大纲。
今年考研专业课826信号处理导论(信号系统和数字信号处理)140,总分410,顺利上岸!回看去年将近一年的复习,还是记忆犹新,有不少经历想和大家分享,有得有失,希望可以对大家复…...

做一个后台项目的架构
后台架构的11个维度 架构1:团队协助基础工具链的选型和培训架构2:搭建微服务开发基础设施架构3:选择合适的RPC框架架构4:选择和搭建高可用的注册中心架构5:选择和搭建高可用的配置中心架构6:选择和搭建高性…...
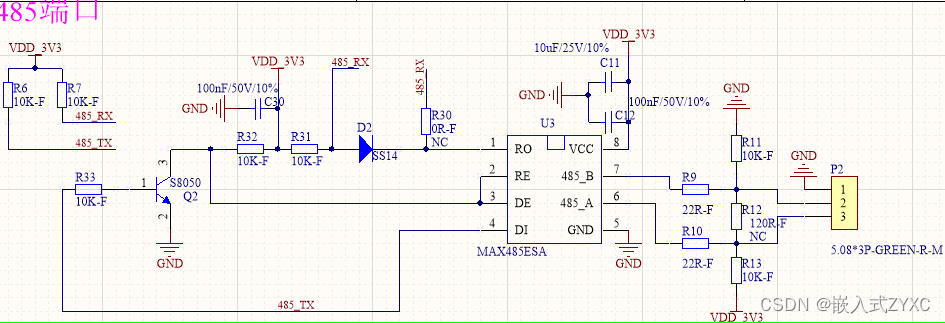
嵌入式单片机 TTL电平、232电平、485电平的区别和联系
一、简介 TTL、232和485是常见的串口通信标准,它们在电平和通信方式上有所不同, ①一般情况下TTL电平应用于单片机外设,属于MCU/CPU等片外外设; ②232/485电平应用于产品整体对外的接口,一般是片外TTL串口转232/485…...
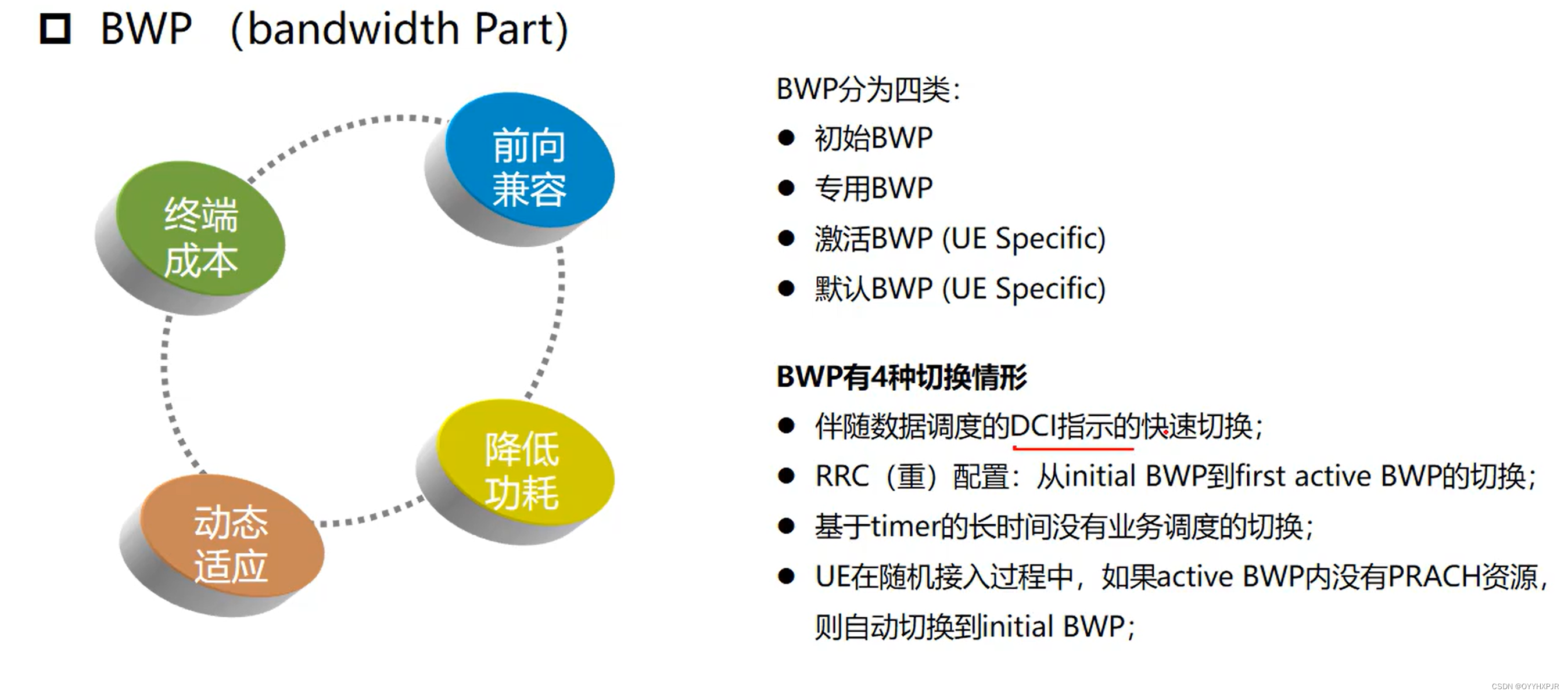
2024年大唐杯备考
努力更新中…… 第一章 网络架构和组网部署 1.1 5G的网络整体架构 5G网络中的中传、回传、前传(这里属于承载网的概念) CU和DU之间是中传 BBU和5GC之间是回传 BBU和AAU之间是前传(这个好记) 这里竟然还藏了MEC(…...
:Spring Boot与MySQL搭配,打造极简高效的数据管理系统)
Spring Boot(06):Spring Boot与MySQL搭配,打造极简高效的数据管理系统
1. 前言 Spring Boot 是一个基于Spring框架的快速开发框架,可以使开发者快速搭建一个可靠的Java Web应用程序。而MySQL是最广泛使用的关系型数据库系统之一,也是Spring Boot整合数据库的首选。本文将介绍Spring Boot如何整合MySQL数据库。 2. 摘要 本文…...

Vue3 + Vite 构建组件库发布到 npm
你有构建完组件库后,因为不知道如何发布到 npm 的烦恼吗?本教程手把手教你用 Vite 构建组件库发布到 npm 搭建项目 这里我们使用 Vite 初始化项目,执行命令: pnpm create vite my-vue-app --template vue这里以我的项目 vue3-xm…...

Vite多环境配置与打包:灵活高效的Vue开发工作流
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...
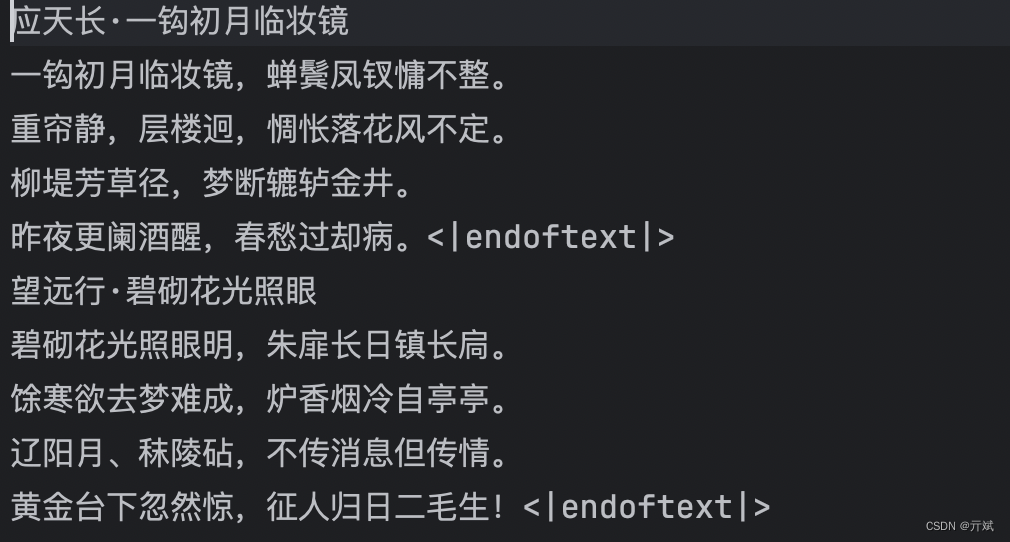
从零实现诗词GPT大模型:数据集介绍和预处理
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 本章将介绍该系列文章中使用的数据集,并且编写预处理代码,处理成咱们需要的格式。 一、数据集介绍 咱们使用的数据集名称是chinese-poetry,是一个在github上开源的中文诗…...
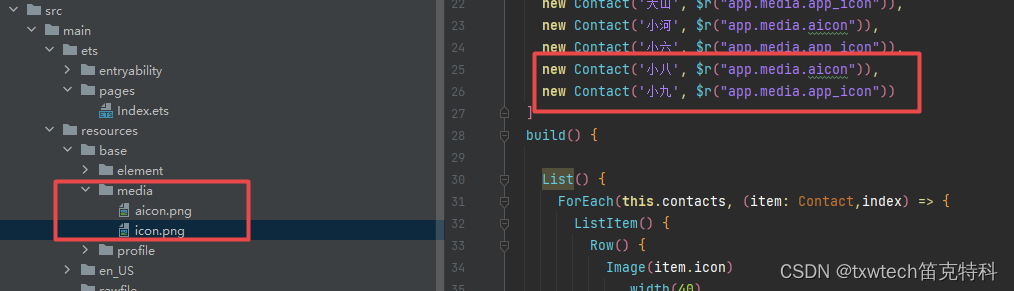
45.HarmonyOS鸿蒙系统 App(ArkUI)创建列表(List)
列表是一种复杂的容器,当列表项达到一定数量,内容超过屏幕大小时,可以自动提供滚动功能。它适合用于呈现同类数据类型或数据类型集,例如图片和文本。在列表中显示数据集合是许多应用程序中的常见要求(如通讯录、音乐列…...

推荐算法之协同过滤
算法原理 透过百科,我们了解到协同过滤推荐(Collaborative Filtering recommendation)是在信息过滤和信息系统中正迅速成为一项很受欢迎的技术。与传统的基于内容过滤直接分析内容进行推荐不同,协同过滤算法结合用户行为分析用户…...

Kotlin 面试题
lifecycleScope.launchWhenResumed launchWhenResumed是一个扩展函数,它是LifecycleCoroutineScope的一部分,并且它是在Android的Lifecycle库中引入的。 这个函数的主要目的是在Lifecycle的对应组件(通常是Activity或Fragment)处于“resumed”状态时启动协程。 public fun …...

TCM(Tightly Coupled Memory)紧密耦合存储器简介
在ARM Cortex处理器中,TCM通常指的是紧密耦合存储器(Tightly Coupled Memory)。TCM是一种位于处理器核心旁边的高速存储器,它的设计目的是为了提供低延迟和高带宽的内存访问性能。 TCM的特点是它与处理器内核紧密耦合,…...

《自动机理论、语言和计算导论》阅读笔记:p172-p224
《自动机理论、语言和计算导论》学习第 8 天,p172-p224总结,总计 53 页。 一、技术总结 1.Context-Free Grammar(CFG) 2.parse tree (1)定义 p183,But perhaps more importantly, the tree, known as a “parse tree”, when used in a …...

typescript playwright 笔记
录制调式 命令 npx playwright codegen url npx playwright codegen https://www.baidu.com/typescript 中 format 和 split 的使用 import * as util from util;const str1 hellow %s; const format util.format; const str2 format(str1, word);// 提取taskId const str3…...

从零实现诗词GPT大模型:了解Transformer架构
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 这篇文档我们开始对GPT的核心组件Transformer进行一个详细的讲解, 加急编写中…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
