低代码开发的优势是什么?
低代码开发的优势是什么?低代码开发这个概念这两年来经常出现在人们的视野中,市场对于低代码的需求也越来越庞大。
Gartner预测,到2025年,75%的大型企业将使用至少四种低代码/无代码开发工具,用于IT应用开发和公民开发计划。
可以看出,低代码确实是受到大家热捧了。
今天就来给大家解答一下——大家为什么追捧低代码开发?低代码开发究竟有什么优势?
01 到底什么是低代码开发?
低代码(Low-code)是一种软件开发方式,它在一定程度上简化了应用程序的开发过程,同时又不完全依赖于编写代码。
低代码平台为开发者提供了不同于传统编码复杂的界面,其具有可视化的开发形式,通过拖放式操作即可生成系统应用程序。
这么说可能还是有点抽象,那我给大家举一个生活中的例子。
如果你想盖一间房子,传统开发就好比你要从从一砖一瓦开始建起,不仅流程复杂,而且耗时很长,并且必须有专业的建筑知识和技能才能进行。
而低代码开发则像活动板房,以标准模数系列进行空间组合即可,可随意拆装、简单迅速,并不要求使用者有非常专业的建筑知识,可以说低代码平台是一套可以重复建造各种房屋的引擎和系统。
因此,利用低代码平台,开发人员能够更快地设计和部署应用程序,从而使组织能够扩展规模、提高盈利能力并获得高于平均水平的回报。
官网:http://s.fanruan.com/ldm67
02 为什么低代码受到市场追捧?
1、企业急需快速轻量工具帮助数字化转型
在新一轮科技革命和产业变革背景下,企业的产业形态与商业模式不断迭代创新,越来越多的企业认识到数字化的重要性。
以制造业为例,不少制造业公司近年在大力发展精益生产,因此对精益办公的需求也越来越高,而传统的办公方式效率低下,拖慢了企业数字化转型的脚步。
因此,借助技术力量进行数字化转型是企业发展的必经之路。
但是对于企业而言存在许多难题:怎么搭建企业应用系统?传统开发太慢、太贵怎么办?我们现在没有可以进行传统开发的人员?......
于是低代码平台应运而生,其可以大幅度提高开发速度,降低了企业的数字化门槛,让企业快速推出数字化应用,提高数字化转型的效率和速度,所以越来越的企业选择低代码平台。
2、IT人才无法满足需求
调研报告显示,有86%的IT部门决策人认为,对公司业务进行数字化转型的最大挑战是IT开发人员太少。
的确,数字化时代企业对于IT人才的需求量极大,但是高端人才又太少,专业素养较低、无工作经验的低端人才比例最大,但是技术不过硬,对于企业来说,培养投入花费太多。
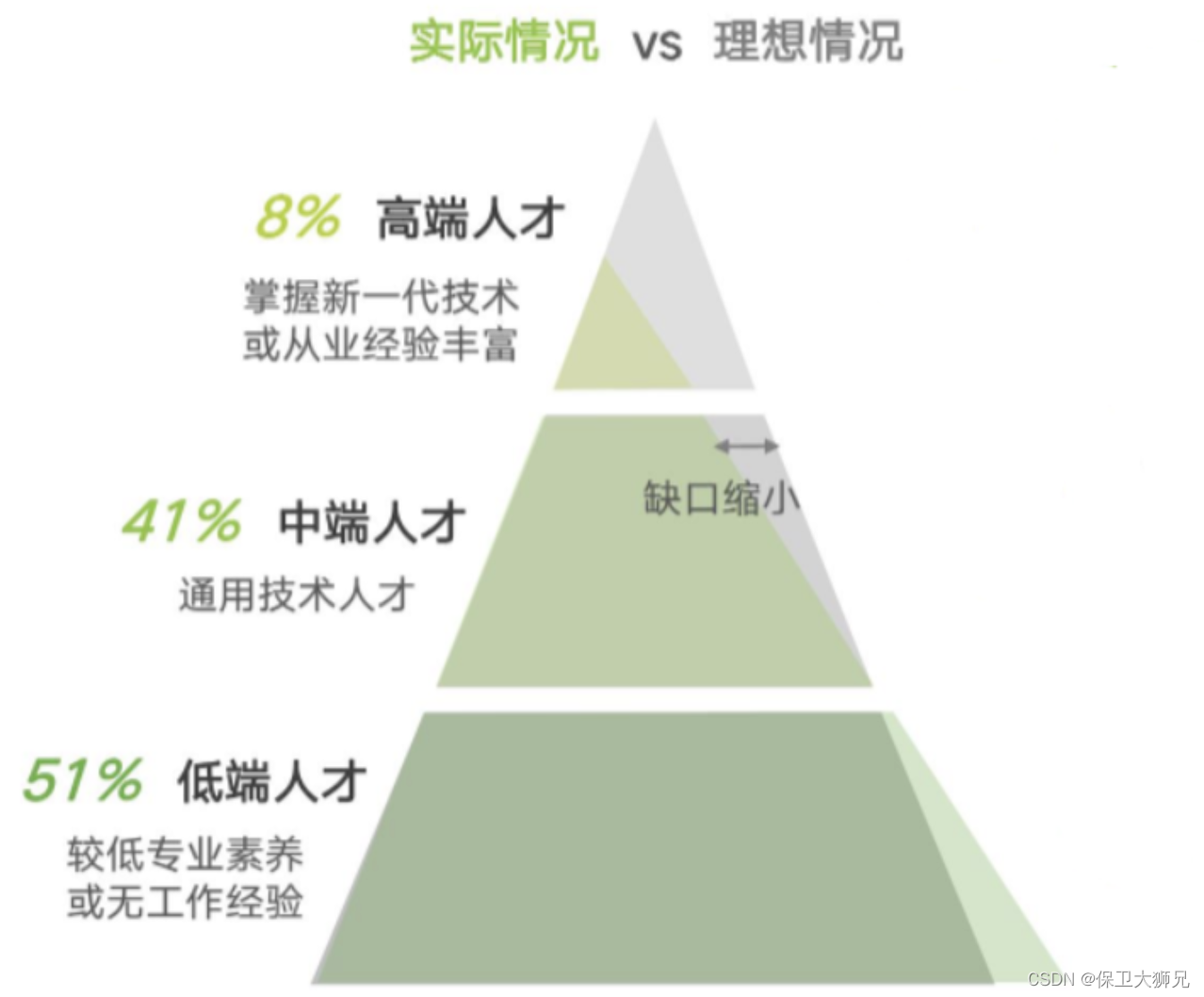
于是,企业中经常出现这样的情况——懂业务规则的人缺乏开发能力,有开发能力的人不了解业务规则,而市场上成熟的软件产品成本高、功能适配度低、迭代周期长,这给企业带来了一大难题。
而低代码平台的出现很好地解决了此类问题,低代码能够赋能并不了解编程知识的业务人员,他们对封装好的代码模块进行拖拉拽即可,能轻松搭建起符合业务需求的应用系统。
在这种环境下,低代码平台如雨后春笋般出现,与此同时,互联网头部厂商也纷纷入局,将低代码推上”风口“,低代码开发迎来了爆发式增量市场。
03 低代码开发到底有什么优势?
1、实现全民开发——人人都能成为开发者
“全民开发”——顾名思义,大量业务部门人员能以开发者的身份,参与到系统的开发、搭建、迭代工作中来。
低代码平台已经告别了传统编程复杂的编码程序,鼠标点击拖拽即可生成应用,只懂一点编码知识甚至是”IT小白“也可以轻松开发应用。并且低代码平台一般会提供详细使用指南、行业参考案例、技术支持等,上手、落地很快。
Gartner在一份分析报告中指出,公民开发将成为业务和 IT 协作的重要组成部分,到2023年,大型企业内的活跃公民开发者数量至少是专业开发者数量的 4 倍。
目前,已经有不少企业开始了”全民开发“的实践。
⭐华锐技术运用简道云零代码能够实现“全民开发”的优势,直接让业务人员进行流程开发。
例如,商务负责开发合同管理相关流程和功能;质量管理人员负责搭建项目相关流程;收入收款则由财务负责。复杂度高的数据分析和流程、整体设计则由企业信息化人员负责。
华锐技术项目搭建的集中投入期只有3个半月左右,平均投入人力约为2人,相对于传统的代码开发来说,利用简道云这种轻量化的低代码平台极大地缩短了开发周期,节约了人力成本。
2、协同能力强
企业业务协作中的每一步操作都会涉及到不同的人和事,以传统办公方式进行,效率必然十分低下,特别在复杂业务流中,一份审批文件,发起人需要多个平台不断传输切换,这就是我们所说的“数据孤岛”。
而通过低代码应用搭建平台,可以有效打破此类困局。由于可以按需搭建,将直接解决各类线上管理需求。不仅省时省力,还能实现数据的有效流通与共享、加强协作。
⭐领科物联网科技有限公司是一家全球 IOT 连接解决方案提供商,其企业员工遍布全球,存在协同能力差的情况。
于是在简道云CRM套件的基础上,领科物联网根据自身的业务完全自定义搭建了项目技术和进销存,解决了企业90%以上的业务需求。
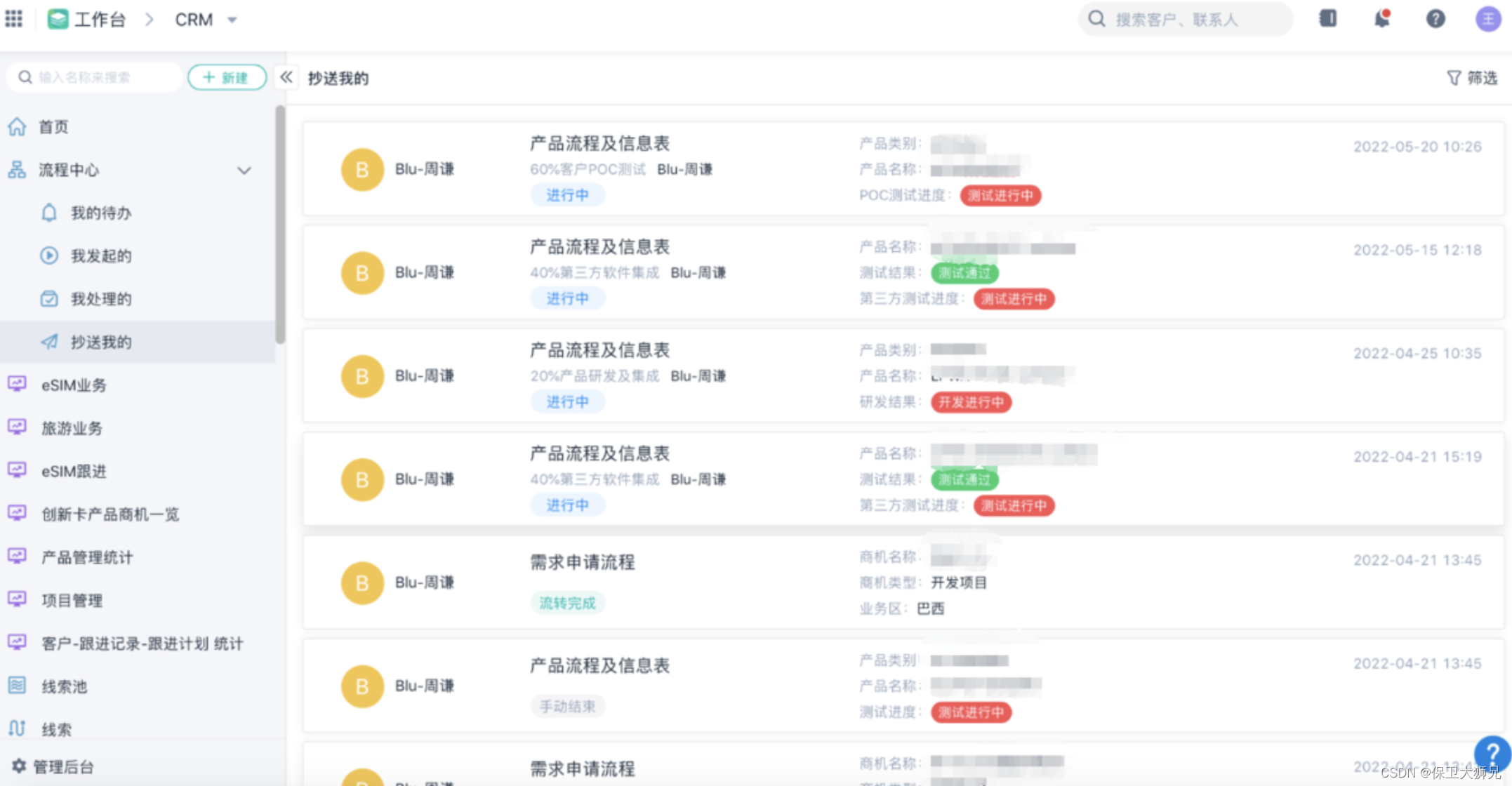
并且,自定义的流程设计使得领科物联网分散在各地的业务和项目人员轻松实现业务往来,构建了人、组织及流程的强效联动平台。
在简道云平台上,只需管理员提前设置好流程的节点、负责人和数据流转的路径。一旦数据提交后,就会进入流程,按照流程的设定进行流转,实现业务流程的规范化与自动化。此外,相关人员还能随时查询工作流程的进度或过往记录。
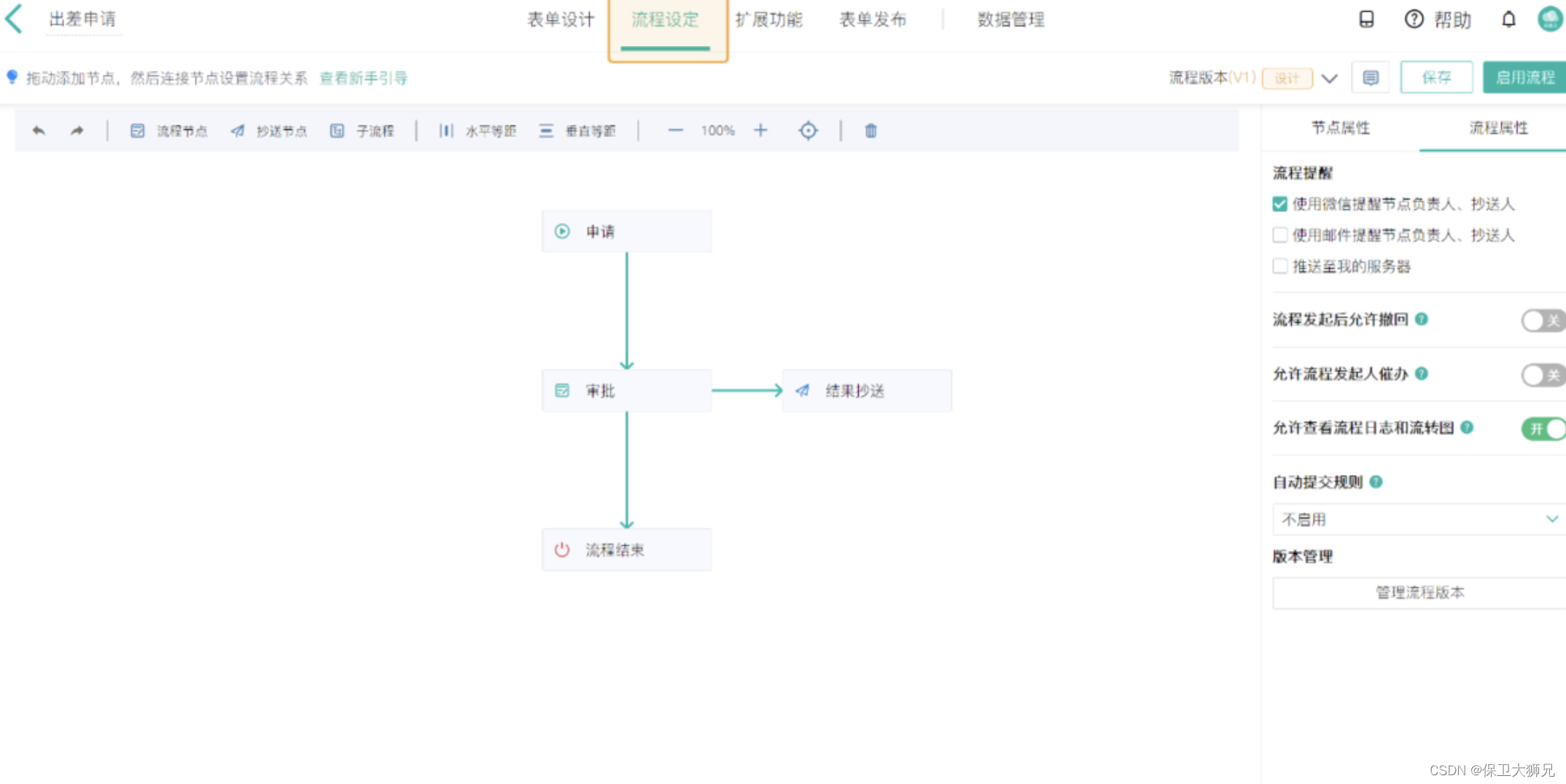
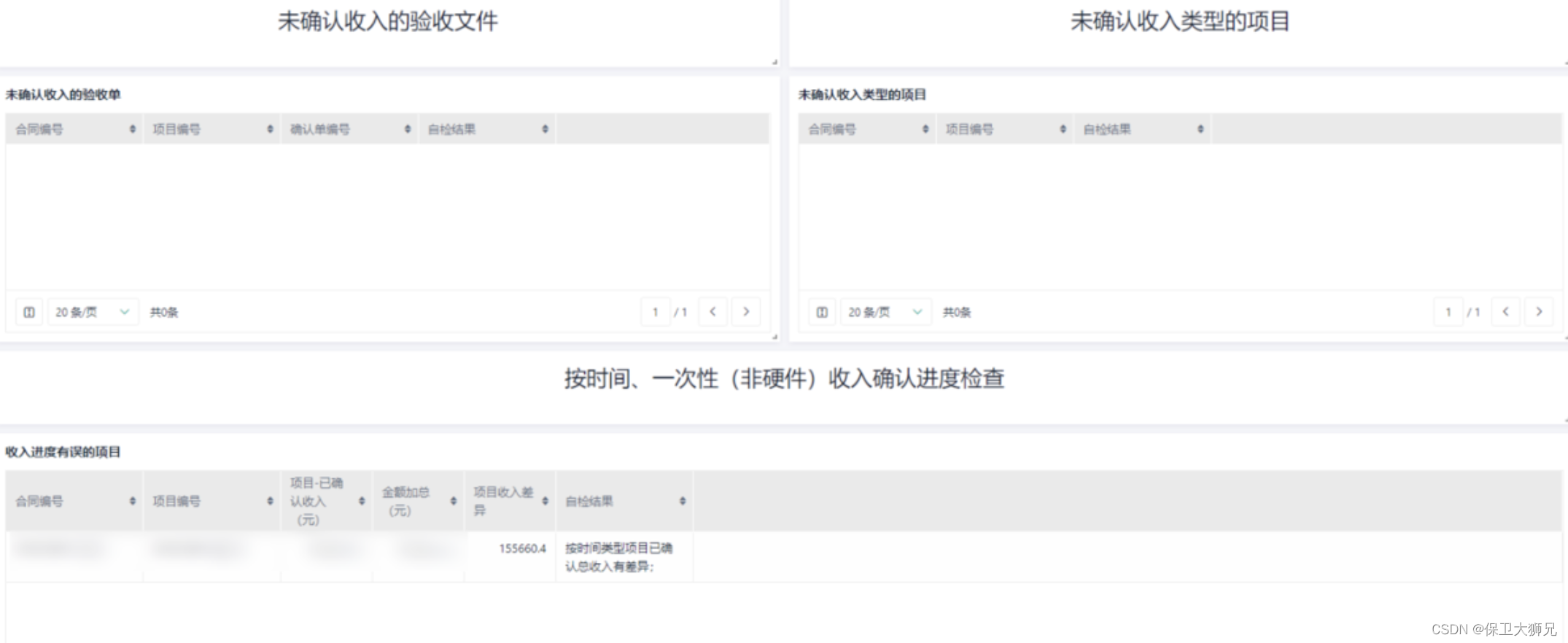
3、成本低,性价比高
目前,市面上企业垂直产品的定制化一般需要几十万到几百万不等的费用,定制化成本对于初创公司来说门槛很高,企业具备一定的研发能力,但如果要依靠研发团队去自研系统,这个成本将会更大。
而利用低代码平台,企业可以”自定义“系统应用,根据自身的业务需求搭建个性化系统,像搭建积木一样轻巧灵活。

并且,订阅式付费的模式成本更低、性价比更高。低代码产品落地快、上线快、迭代快,在公司正式开始使用产品前,几乎没有任何沉默成本(不考虑机会成本),实施成本极低。
同时产品试错成本低,零代码的SaaS模式下如果对于产品不满意,也能以较低的成本转换到别的平台。
⭐领科物联网科技有限公司利用简道云完成了90%以上的业务需求,但实现成本仅是其他垂直产品的1/10,是自研成本的1%。
因此,可以预见的是,低代码开发不仅会保留下来,而且会成为未来企业数字化转型的有力工具。
读完本文,您是否对于低代码开发有了更深层次的了解呢?
相关文章:

低代码开发的优势是什么?
低代码开发的优势是什么?低代码开发这个概念这两年来经常出现在人们的视野中,市场对于低代码的需求也越来越庞大。 Gartner预测,到2025年,75%的大型企业将使用至少四种低代码/无代码开发工具,用于IT应用开发和公民开发计划。 可…...

Ip2Resion线上部署报数据越界及错误处理
上篇在本地测试调用Ip2Resigon解析行政区划 Ip2Region的Java本地实现运行正常,但部署到测试环境,抛出数组越界(java.lang.ArrayIndexOutOfBoundsException)异常。 环境信息 ip2Resion是2.7版本,对应文件后缀为 xdb。 …...

致敬我的C++启蒙老师,跟着他学计算机编程就对了 (文末赠书5本)
致敬我的C启蒙老师,跟着他学计算机编程就对了 摘要 讲述了一个故事,介绍了一位良师,一段因C而续写的回忆,希望对各位看官有所帮助和启发。 文章目录1 写在前面2 我的C启蒙老师3 谈谈老师给我的启发4 友情推荐5 文末福利1 写在前面…...

CSS中的伪元素和伪类
一直被伪类和伪元素所迷惑,以为是同一个属性名称,根据CSS动画,索性开始研究a:hover:after,a.hover:after的用法。 伪元素 是HTML中并不存在的元素,用于将特殊的效果添加到某些选择器。 对伪元素的描述 伪元素有两…...

逻辑优化基础-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
案例27-单表从9个更新语句调整为2个
目录 一:背景介绍 二:思路&方案 三:过程 1.项目结构 2.准备一个普通的maven项目,部署好mysql数据库 3.在项目中引入pom依赖 5.编写MyBitis配置文件 6.编写Mysql配置类 7.编写通用Update语句 8.项目启动类 四:总…...

Wordpress paid-memberships-pro plugins CVE-2023-23488未授权SQLi漏洞分析
目录 1.漏洞概述 2.漏洞等级 3.调试环境 4.漏洞代码 5 POC 1.漏洞概述 WordPress插件paid-memberships-pro版本<2.9.8中,容易受到REST路由“/pmpro/v1/order”的“code”参数中未验证的SQL注入漏洞的影响。攻击者可进行SQLi盲注,从而获取数据库权限。 CVE:...

【JavaWeb篇】JSTL相关知识点总结
目录 为什么会有JSTL? 什么是JSTL? 如何理解JSTL标准标签库呢? 如何使用JSTL? 第一步:引入JSTL标签库对应的jar包。 第二步:在JSP中引入要使用标签库。(使用taglib指令引入标签库。&#x…...

【蓝桥杯刷题】坑爹的负进制转换
【蓝桥杯刷题】——坑爹的负进制转换😎😎😎 目录 💡前言🌞: 💛坑爹的负进制转换题目💛 💪 解题思路的分享💪 😊题目源码的分享Ƕ…...

react+antdpro+ts实现企业级项目二:Strapi及认证登陆模块
在上一章节中,我们已经成功创建并登陆了系统,现在需要为系统添加权限和登录认证,以提高系统的安全性、数据保护、个性化服务和用户体验。此外,添加权限和登录认证还可以方便管理员进行用户和授权管理。为了快速开发前端࿰…...

Android ANR trace日志如何导出
什么是ANR ?上网搜索,一搜一大片,我就说个很容易识别的字眼,XXXAPP无响应 ANR trace日志如何导出?使用ADB命令: adb pull data/anr/trace.txt 你要存放的路径。查看ANR报错位置全局搜索你APP的包名&#x…...

Windows SSH 配置和SCP的使用
使用用户界面安装 ssh 功能 要在 Windows 10/11 上启用 SSH 服务器,请按照以下步骤操作: 按“Windows 键 I”打开“设置”菜单,然后选择“应用程序”。在左侧菜单栏中选择“应用和功能”。从列表中选择“可选功能”。 点击“添加功能”按钮…...

liunx 安装redsi和连接
liunx 安装redsi和连接 下载 (https://download.redis.io/releases/) 上传到 /usr/local目录 解压 tar -xvf redis-5.0.14.tar.gz 切换到 cd ./redis-5.0.14 编译 make 安装 make install 默认安装目录 /usr/local/bin/ 修改 ./redis-5.0.14/reds…...
接口里面可以写实现方法吗【可以】 、接口可以多继承吗【可以】
比如下面这道题: 问: 接口里面可以写方法吗? 答: 当然可以啊,默认就是抽象方法。 . 问: 那接口里面可以写实现方法吗? 答: 不可以,所有方法必须是抽象的。 . 问: 你确定吗࿱…...
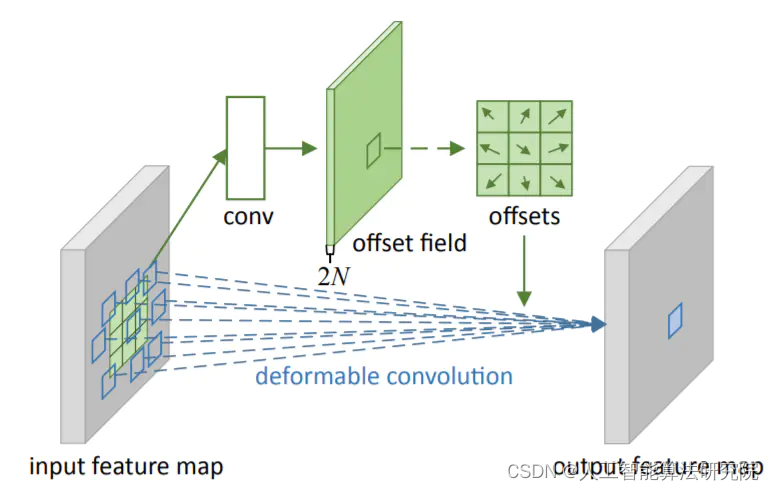
【YOLOv8/YOLOv7/YOLOv5/YOLOv4/Faster-rcnn系列算法改进NO.57】引入可形变卷积
文章目录前言一、解决问题二、基本原理三、添加方法四、总结前言 作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列…...
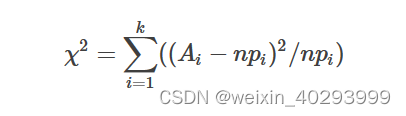
统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的…...
基于Django4.1.4的入门学习记录
基于Django4.1.4的入门学习记录Django创建Django项目创建工程工程目录说明运行开发服务器settings.py配置文件应用的创建创建应用模块应用模块文件说明App应用配置注册安装子应用数据模型ORM概述定义模型类生成数据库表查看数据库文件Admin管理工具管理界面本地化创建管理员注册…...

C++ Butterworth N阶滤波器设计
介绍一个 Butterworth Nth 滤波器设计系数的函数,像 Matlab 函数一样的: [bl,al]butter(but_order,Ws); 和 [bh,ah]butter(but_order,2*bandwidth(1)/fs,high);rtfilter 在 Ububtu 中,容易找到: $ aptitude search ~dbutterwo…...

UXP下不用任何框架创建自己的插件并试运行
在上一篇文章中《Windows下vue框架下的UXP插件开发环境搭建及程序试运行》,搭建的是利用vue框架进行开发的UXP开发环境,而且是把官方的案例插件直接添加进UDT,下面要说的是不利用任何js的框架创建和试运行自己的UXP插件程序,这样来…...

mac修改国内源快速安装brew
我是参考了清华源官网,有任何困惑直接访问该网址即可。这里给出精简版。 1. 更改镜像到~/.zshrc 终端添加方式 echo export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" >> ~/.zshrcecho export HOMEBREW_…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
