【信号与系统 - 9】傅里叶变换的性质习题
1 习题
已知 f ( t ) f(t) f(t) 的傅里叶变换为 F ( j w ) F(jw) F(jw) ,求如下信号的傅里叶变换
-
(1) t ⋅ f ( 3 t ) t\cdot f(3t) t⋅f(3t)
解:
f ( 3 t ) ↔ 1 3 F ( j w 3 ) f(3t)\leftrightarrow \frac{1}{3}F(j\frac{w}{3}) f(3t)↔31F(j3w)
t ⋅ f ( 3 t ) ↔ j 1 3 ⋅ d d w [ F ( j w 3 ) ] t\cdot f(3t)\leftrightarrow j\frac{1}{3}\cdot\frac{d}{dw}[F(j\frac{w}{3})] t⋅f(3t)↔j31⋅dwd[F(j3w)]
其中: d ( w 3 ) = 1 3 d w d(\frac{w}{3})=\frac{1}{3}dw d(3w)=31dw,则 d w = 3 d ( w 3 ) dw=3d(\frac{w}{3}) dw=3d(3w),所以 d d w [ F ( j w 3 ) ] = 1 3 d d ( w 3 ) [ F ( j w 3 ) ] \frac{d}{dw}[F(j\frac{w}{3})]=\frac{1}{3}\frac{d}{d(\frac{w}{3})}[F(j\frac{w}{3})] dwd[F(j3w)]=31d(3w)d[F(j3w)],则 t ⋅ f ( 3 t ) ↔ j 1 9 ⋅ F ′ ( j w 3 ) t\cdot f(3t)\leftrightarrow j\frac{1}{9}\cdot F'(j\frac{w}{3}) t⋅f(3t)↔j91⋅F′(j3w) -
(2) ( t − 1 ) d [ f ( t ) ] d t (t-1)\frac{d[f(t)]}{dt} (t−1)dtd[f(t)]
解:
d [ f ( t ) ] d t ↔ j w F ( j w ) \frac{d[f(t)]}{dt}\leftrightarrow jwF(jw) dtd[f(t)]↔jwF(jw)
t ⋅ d [ f ( t ) ] d t ↔ j d d w [ j w F ( j w ) ] = − d d w [ w F ( j w ) ] = − [ F ( j w ) + w F ′ ( j w ) ] t\cdot\frac{d[f(t)]}{dt}\leftrightarrow j\frac{d}{dw}[jwF(jw)]=-\frac{d}{dw}[wF(jw)]=-[F(jw)+wF'(jw)] t⋅dtd[f(t)]↔jdwd[jwF(jw)]=−dwd[wF(jw)]=−[F(jw)+wF′(jw)]
( t − 1 ) ⋅ d [ f ( t ) ] d t ↔ j d d w [ j w F ( j w ) ] = − d d w [ w F ( j w ) ] = − [ F ( j w ) + w F ′ ( j w ) ] − j F ′ ( j w ) = − [ F ( j w ) + ( w + 1 ) F ′ ( j w ) ] (t-1)\cdot\frac{d[f(t)]}{dt}\leftrightarrow j\frac{d}{dw}[jwF(jw)]=-\frac{d}{dw}[wF(jw)]=-[F(jw)+wF'(jw)]-jF'(jw)=-[F(jw)+(w+1)F'(jw)] (t−1)⋅dtd[f(t)]↔jdwd[jwF(jw)]=−dwd[wF(jw)]=−[F(jw)+wF′(jw)]−jF′(jw)=−[F(jw)+(w+1)F′(jw)]
- (3) ( 2 − t ) f ( 2 − t ) (2-t)f(2-t) (2−t)f(2−t)
解:
f ( 2 − t ) = f [ − ( t − 2 ) ] ↔ F ( − j w ) e − j 2 w f(2-t)=f[-(t-2)]\leftrightarrow F(-jw)e^{-j2w} f(2−t)=f[−(t−2)]↔F(−jw)e−j2w
t ⋅ f ( 2 − t ) ↔ j d d w [ F ( − j w ) e − j 2 w = − j d d ( − w ) [ F ( − j w ) e − j 2 w ] = − j [ F ′ ( − j w ) e − j 2 w − j 2 F ( − j w ) e − j 2 w ] t\cdot f(2-t)\leftrightarrow j\frac{d}{dw}[F(-jw)e^{-j2w}=-j\frac{d}{d(-w)}[F(-jw)e^{-j2w}]=-j\Big[F'(-jw)e^{-j2w}-j2F(-jw)e^{-j2w}\Big] t⋅f(2−t)↔jdwd[F(−jw)e−j2w=−jd(−w)d[F(−jw)e−j2w]=−j[F′(−jw)e−j2w−j2F(−jw)e−j2w]
( 2 − t ) ⋅ f ( 2 − t ) ↔ 2 F ( − j w ) e − j 2 w + [ j F ′ ( − j w ) e − j 2 w − 2 F ( − j w ) e − j 2 w ] = j F ′ ( − j w ) e − j 2 w (2-t)\cdot f(2-t)\leftrightarrow 2F(-jw)e^{-j2w}+[jF'(-jw)e^{-j2w}-2F(-jw)e^{-j2w}]=jF'(-jw)e^{-j2w} (2−t)⋅f(2−t)↔2F(−jw)e−j2w+[jF′(−jw)e−j2w−2F(−jw)e−j2w]=jF′(−jw)e−j2w
2 补充:二倍角以及积化和差公式
{ c o s α ⋅ c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] 【调制】 s i n α ⋅ s i n β = 1 2 [ c o s ( α + β ) − c o s ( α − β ) ] c o s α ⋅ s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] s i n α ⋅ c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] \begin{cases} cos\alpha \cdot cos\beta=\frac{1}{2}[cos(\alpha+\beta)+cos(\alpha-\beta)]【调制】\\ sin\alpha \cdot sin\beta=\frac{1}{2}[cos(\alpha+\beta)-cos(\alpha-\beta)]\\ cos\alpha \cdot sin\beta=\frac{1}{2}[sin(\alpha+\beta)-sin(\alpha-\beta)]\\ sin\alpha \cdot cos\beta=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)]\\ \end{cases} ⎩ ⎨ ⎧cosα⋅cosβ=21[cos(α+β)+cos(α−β)]【调制】sinα⋅sinβ=21[cos(α+β)−cos(α−β)]cosα⋅sinβ=21[sin(α+β)−sin(α−β)]sinα⋅cosβ=21[sin(α+β)+sin(α−β)]
s i n ( 2 α ) = 2 s i n α ⋅ c o s α sin(2\alpha)=2sin\alpha\cdot cos\alpha sin(2α)=2sinα⋅cosα
{ c o s ( 2 α ) = 2 c o s 2 α − 1 = 1 − 2 s i n 2 α = c o s 2 α − s i n 2 α c o s 2 α = c o s ( 2 α ) + 1 2 s i n 2 α = 1 − c o s ( 2 α ) 2 \begin{cases} cos(2\alpha)=2cos^2\alpha-1=1-2sin^2\alpha=cos^2\alpha-sin^2\alpha\\ cos^2\alpha=\frac{cos(2\alpha)+1}{2}\\ sin^2\alpha=\frac{1-cos(2\alpha)}{2}\\ \end{cases} ⎩ ⎨ ⎧cos(2α)=2cos2α−1=1−2sin2α=cos2α−sin2αcos2α=2cos(2α)+1sin2α=21−cos(2α)
t a n ( 2 α ) = 2 t a n α 1 − t a n 2 α tan(2\alpha)=\frac{2tan\alpha}{1-tan^2\alpha} tan(2α)=1−tan2α2tanα
相关文章:

【信号与系统 - 9】傅里叶变换的性质习题
1 习题 已知 f ( t ) f(t) f(t) 的傅里叶变换为 F ( j w ) F(jw) F(jw) ,求如下信号的傅里叶变换 (1) t ⋅ f ( 3 t ) t\cdot f(3t) t⋅f(3t) 解: f ( 3 t ) ↔ 1 3 F ( j w 3 ) f(3t)\leftrightarrow \frac{1}{3}F(j\frac{w}…...
:语法糖概念解析)
C#探索之路基础夯实篇(5):语法糖概念解析
C#探索之路基础夯实篇(5):语法糖概念解析 文章目录 C#探索之路基础夯实篇(5):语法糖概念解析1、概念定义2、Lua中的语法糖3、C#中的语法糖4、C中的语法糖5、优缺点辨析6、适用范围7、总结 从之前一开始接触lua的时候开始,开始第一次接触到语法…...
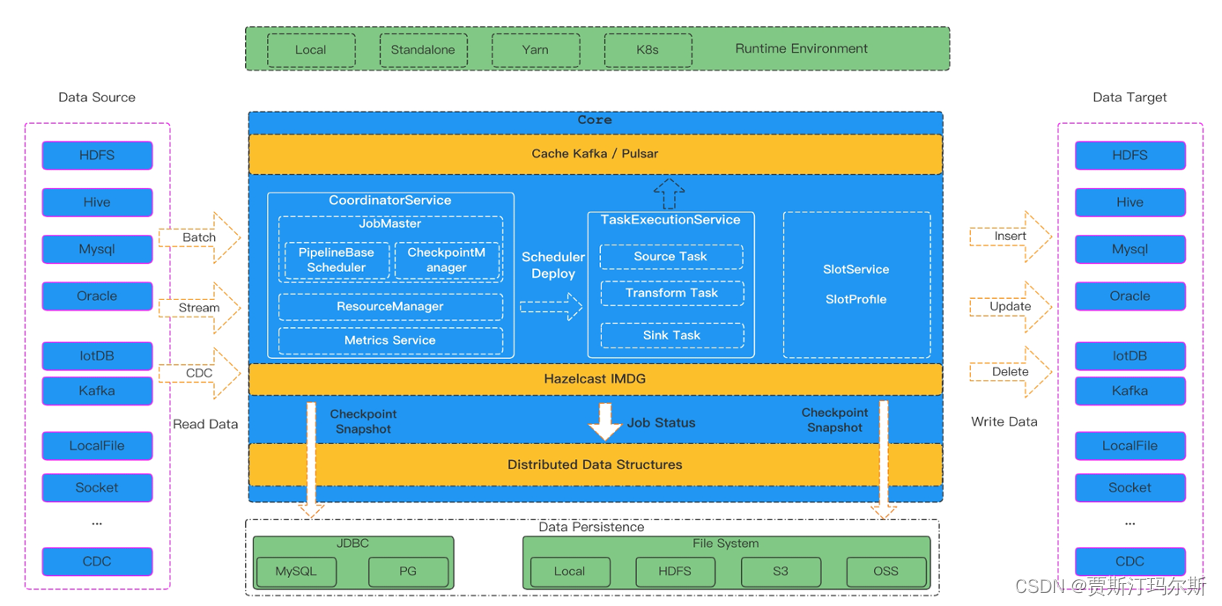
SeaTunnel 与 DataX 、Sqoop、Flume、Flink CDC 对比
产品概述 Apache SeaTunnel 是一个非常易用的超高性能分布式数据集成产品,支持海量数据的离线及实时同步。每天可稳定高效同步万亿级数据,已应用于数百家企业生产,也是首个由国人主导贡献到 Apache 基金会的数据集成顶级项目。 SeaTunnel 主要解决数据集成领域的常见问题:…...

深入理解汇编:平栈、CALL和RET指令详解
视频学习下载地址:https://pan.quark.cn/s/04e6946a803a 汇编语言以其接近硬件的特性和高效的执行速度,在系统编程、性能优化和逆向工程中占有不可或缺的地位。本文将深入探讨汇编语言中的平栈操作以及CALL和RET指令&#…...
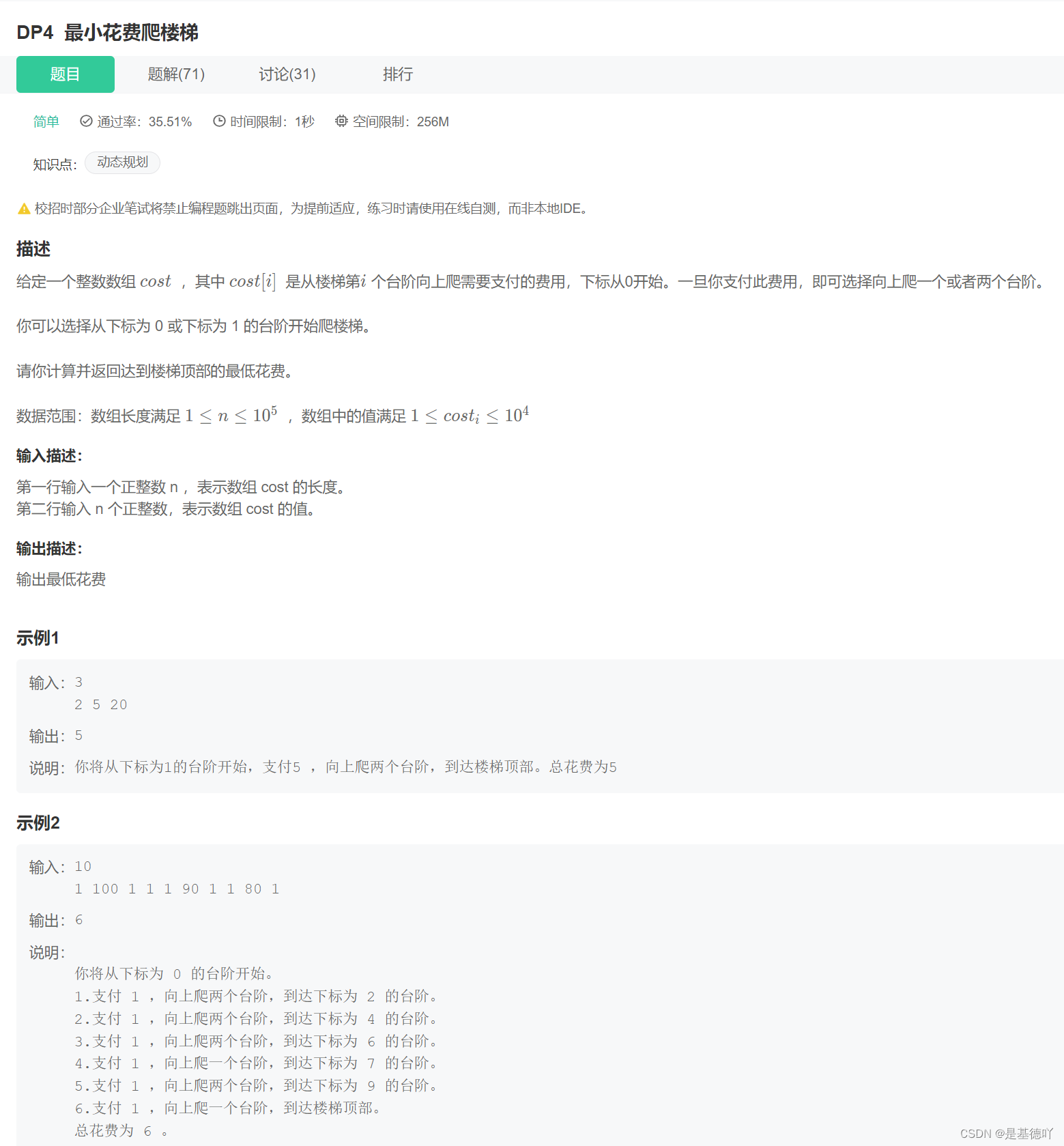
DP4 最小花费爬楼梯
原题链接:最小花费爬楼梯_牛客题霸_牛客网 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 dp。 开一个dp数组和a数组。dp[i]表示在当前这一格所需要的费用,a数组其实就是题目中的cost数组。 因为最后要求到顶楼的最低费用&a…...

OpenXR API概览与核心组件解析
在虚拟现实(VR)和增强现实(AR)领域,OpenXR API提供了一个重要的开放标准,使得开发者能够跨多种硬件和软件平台创建兼容的应用。本文将详细解释OpenXR中的核心组件和数据结构,并探讨它们如何共同…...
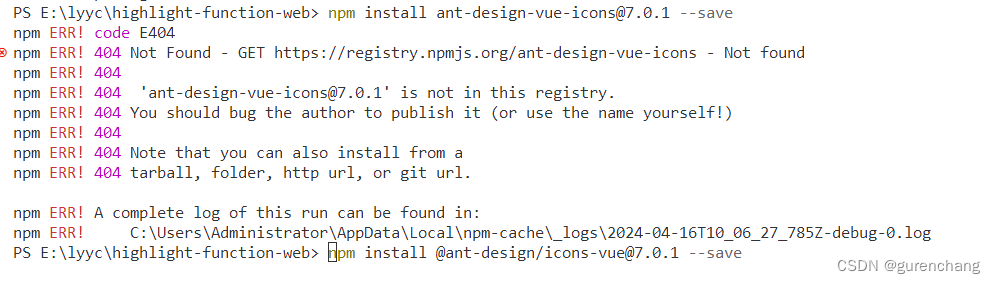
安装指定版本的ant-design-vue和指定版本的@ant-design/icons-vue 图标组件包
前言: 最近在完成公司的项目时,为了兼容其他的版本,需要安装指定版本的ant-design-vue和ant-design/icons-vue 图标组件包,安装成功之后,分享如下: 安装命令: ant-design-vue: 不…...

Zynq7000系列中的休眠模式
休眠模式是在系统层面定义的,它包括将APU置于待机模式,并将多个控制器保持在无时钟的复位状态。 进入休眠模式可以大大降低功耗。在休眠模式下,大多数功能时钟组都会被关闭或断电。唯一需要保持活动的设备是一个CPU、窥探控制单元(…...

在redhat7/8平台上部署ELK7.17.18的技术方案
部署环境说明 为节省资源直接使用1台测试机模拟3节点elasticsearch服务集群做部署,在该主机上同时部署了3个elasticsearch实例、1个logstash实例、1个kibana实例、1个filebeat实例。对于生产环境,以上实例服务应该做分布式部署。 ELK-TEST1 192.168.10…...
分享6个好用的ChatGPT)
(Chat For Al,创新Al,汇语Al助手,AiTab新标签,万能助手,LLaVA)分享6个好用的ChatGPT
目录 1、Chat For AI 2、创想AI 3、汇语AL助手...

MySQL-锁篇
文章目录 表级锁和行级锁了解吗?有什么区别?行级锁使用有什么注意事项?InnoDB有哪几类行锁?共享锁和排他锁是什么?意向锁有什么用? 锁是一种常见的并发事务的控制方式 表级锁和行级锁了解吗?有什…...

滤波器笔记(杂乱)
线性相位是时间平移,相位不失真 零、基础知识 1、用相量表示正弦量 https://zhuanlan.zhihu.com/p/345546880 https://www.zhihu.com/question/347763932/answer/1103938667 A s i n ( ω t θ ) ⇔ A e j θ ⇔ A ∠ θ Asin(\omega t\theta) {\Leftrightarrow…...
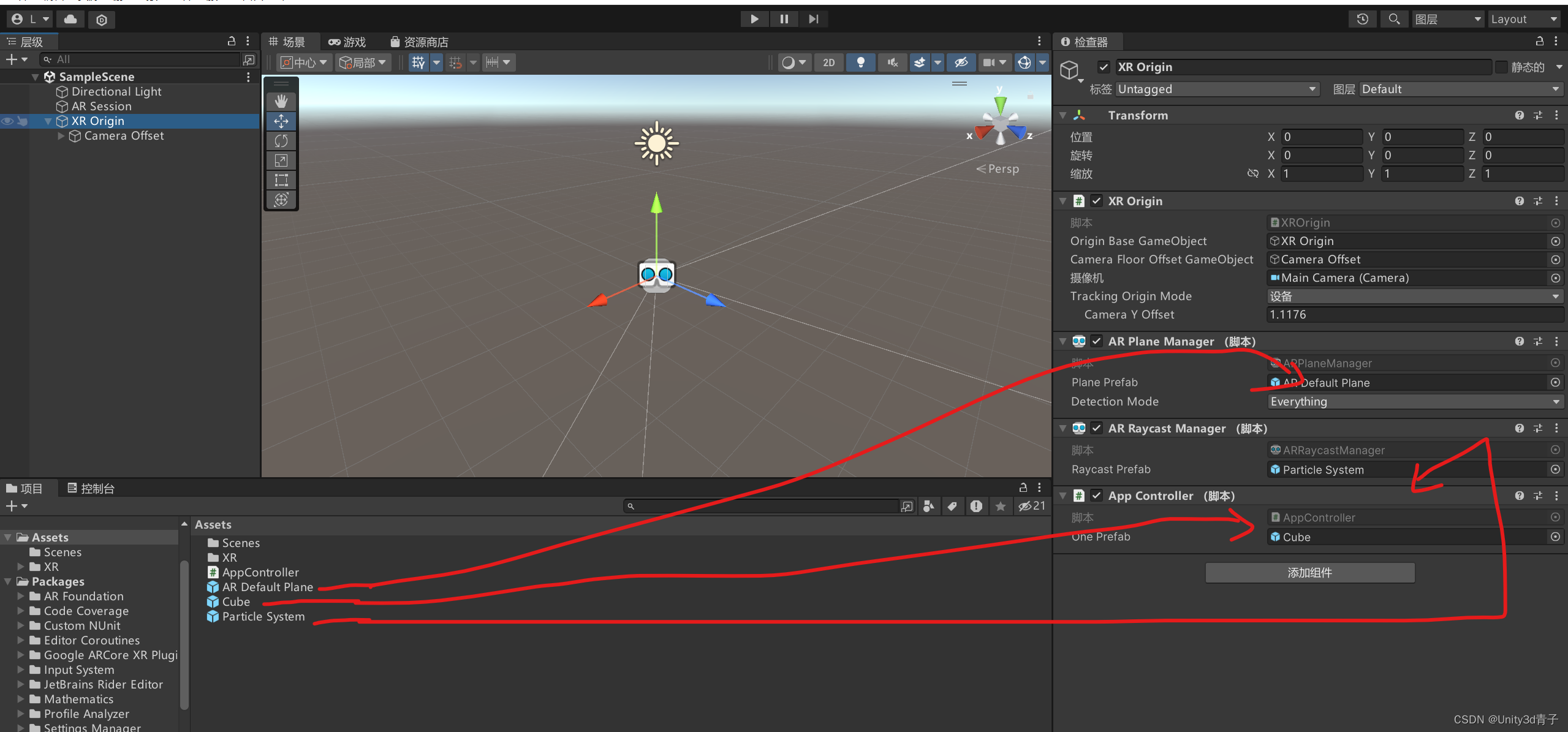
【ARFoundation自学01】搭建AR框架,检测平面点击位置克隆物体
Unity开发ARFoundation相关应用首先安装ARFoundation包 然后设置XR 1.基础AR场景框架搭建 2.一个基本的点击克隆物体到识别的平面脚本 挂在XROrigin上 脚本AppController 脚本说明书 ## 业务逻辑 AppController 脚本旨在实现一个基本的 AR 应用程序功能:用户通过…...

.Net ajax 接收参数
后端部分代码 一般处理程序 public void ProcessRequest(HttpContext context){context.Response.ContentType "text/plain";string str_index context.Request.Form.AllKeys.Contains("index") ? context.Request.Form["index"].ToString(…...

智能零售:引领购物新时代
智能零售通过整合人工智能、物联网、大数据和机器学习等技术,正在彻底改变传统的购物模式,为消费者和零售商提供前所未有的效率和个性化体验。 智能零售利用消费者数据分析来提供个性化的购物推荐。无论是在线平台或是实体店内,智能系统都能…...

【AIGC】AIGC在虚拟数字人中的应用:塑造未来互动体验的革新力量
🚀 🚀 🚀随着科技的快速发展,AIGC已经成为引领未来的重要力量。其中,AIGC在虚拟数字人领域的应用更是引起了广泛关注。虚拟数字人作为一种先进的数字化表达形式,结合了3D建模、动画技术、人工智能等多种先进…...

电机控制器电路板布局布线参考指导(五)
电机控制器电路板布局布线参考指导(五)大容量电容和旁路电容的放置 1.大容量电容的放置2.电荷泵电容器3.旁路电容/去耦电容的放置3.1 靠近电源3.2 靠近功率器件3.3 靠近开关电流源3.4 靠近电流感测放大器3.5 靠近稳压器 tips:资料主要来自网络…...

Python医院挂号脚本
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。 会一些的技术:数据分析、算法、SQL、大数据相关、python 欢迎加入社区:码上找工作 作者专栏每日更新: LeetCode解锁1000题: 打怪升级之旅 python数据分析…...
LabVIEW光学探测器板级检测系统
LabVIEW光学探测器板级检测系统 特种车辆乘员舱的灭火抑爆系统广泛采用光学探测技术来探测火情。光学探测器作为系统的关键部件,其探测灵敏度、响应速度和准确性直接关系到整个系统的运行效率和安全性。然而,光学探测器在长期使用过程中可能会因为灰尘污…...
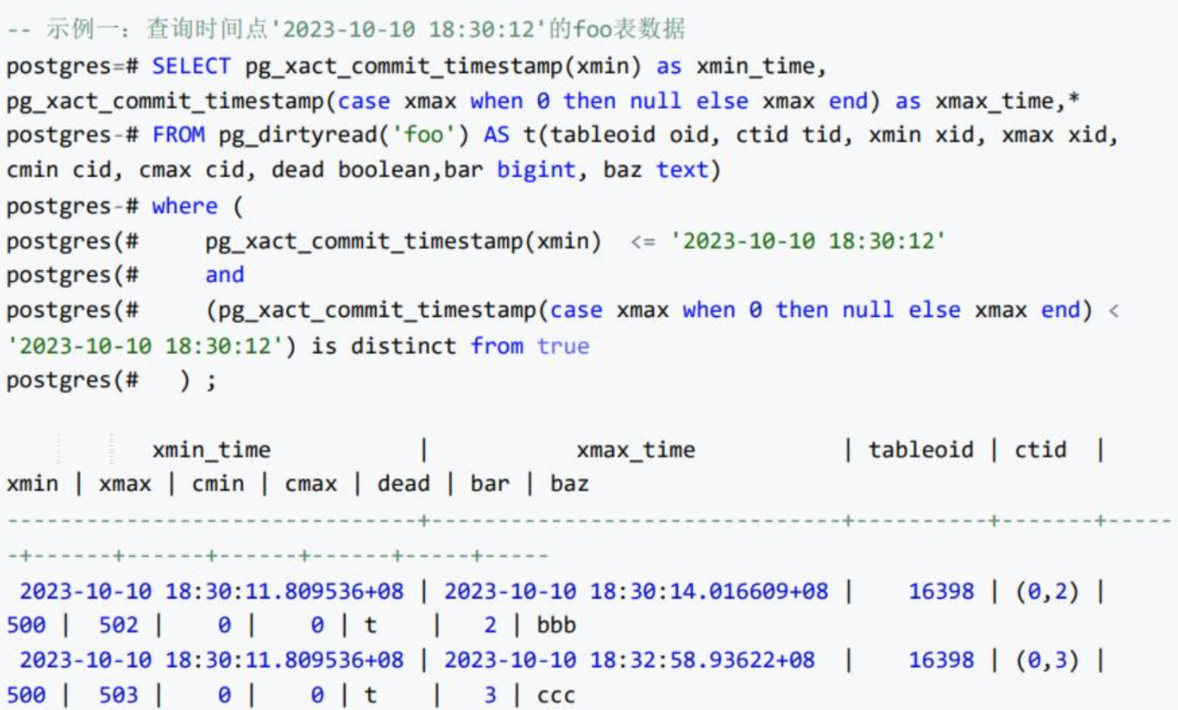
女上司问我:误删除PG百万条数据,可以闪回吗?
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验 擅长主流数据Oracle、MySQL、PG、openGauss运维 备份恢复,安装迁移,性能优化、故障应急处理等可提供技术业务: 1.DB故障处理/疑难杂症远程支援 2.Mysql/PG/Oracl…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
