数组中的逆序对

解题思路1:
看到这个题目,我们的第一反应是顺序扫描整个数组。每扫描到一个数组的时候,逐个比较该数字和它后面的数字的大小。如果后面的数字比它小,则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和O(n)这个数字比较,因此这个算法的时间复杂度为O(n^2)。
我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候,我们不拿ta和后面的每一个数字作比较,否则时间复杂度就是O(n^2),因此我们可以考虑先比较两个相邻的数字。
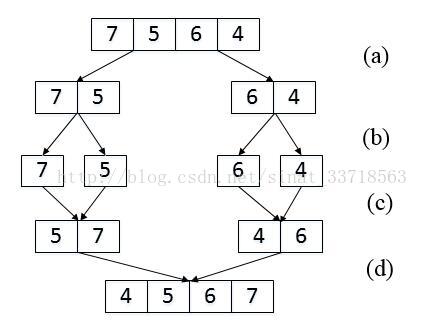
(a) 把长度为4的数组分解成两个长度为2的子数组;
(b) 把长度为2的数组分解成两个成都为1的子数组;
(c) 把长度为1的子数组 合并、排序并统计逆序对 ;
(d) 把长度为2的子数组合并、排序,并统计逆序对;
在上图(a)和(b)中,我们先把数组分解成两个长度为2的子数组,再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组,一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5,因此(7,5)组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对(6,4)。由于我们已经统计了这两对子数组内部的逆序对,因此需要把这两对子数组 排序 如上图(c)所示, 以免在以后的统计过程中再重复统计。
接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。
我们先用两个指针分别指向两个子数组的末尾,并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字,则构成逆序对,并且逆序对的数目等于第二个子数组中剩余数字的个数,如下图(a)和(c)所示。如果第一个数组的数字小于或等于第二个数组中的数字,则不构成逆序对,如图b所示。每一次比较的时候,我们都把较大的数字从后面往前复制到一个辅助数组中,确保 辅助数组(记为copy) 中的数字是递增排序的。在把较大的数字复制到辅助数组之后,把对应的指针向前移动一位,接下来进行下一轮比较。

过程:先把数组分割成子数组,先统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序。如果对排序算法很熟悉,我们不难发现这个过程实际上就是归并排序。
public class Solution {public int InversePairs(int [] array) {if(array == null || array.length == 0){return 0;}//和array长度一样的copy数组int[] copy = new int[array.length];int count = inversePairsCore(array, copy, 0, array.length - 1);return count;}public int inversePairsCore(int[] array, int[] copy, int low, int high){if(low == high){return 0;}//计算中间下标int mid =(low + high)>>1;//中间下标int i = mid;//最大下标int j = high;//copy数组的最大下标int indexCopy = high;//获得左边数组的逆序对int leftCount = inversePairsCore(array, copy, low, mid)%1000000007;//获得右边数组的逆序对int rightCount = inversePairsCore(array, copy, mid + 1, high)%1000000007;int count = 0;while(i >= low && j > mid){if(array[i] > array[j]){//计算逆序对count += j - mid;//左边数组向左移动一位,并将值存入copy中copy[indexCopy]=array[i--];if(count >= 1000000007){count%=1000000007;}}else{//右边数组向左移动一位,并将值存入copy中copy[indexCopy]=array[j--];}indexCopy--;}//左边剩余数组存入到copy中for(; i >= low; i--){copy[indexCopy--] = array[i];}//右边剩余数组存入到copy中for(; j > mid; j--){copy[indexCopy--] = array[j];}//将排过序的数组在array中同步for(int s = low; s <= high; s++){array[s] = copy[s];}return (leftCount + rightCount + count)%1000000007;}
}
相关文章:

数组中的逆序对
解题思路1: 看到这个题目,我们的第一反应是顺序扫描整个数组。每扫描到一个数组的时候,逐个比较该数字和它后面的数字的大小。如果后面的数字比它小,则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和…...
C++基础了解-01-基础语法
基础语法 一、基础语法 C 程序可以定义为对象的集合,这些对象通过调用彼此的方法进行交互。现在让我们简要地看一下什么是类、对象,方法、即时变量。 对象 - 对象具有状态和行为。例如:一只狗的状态 - 颜色、名称、品种,行为 -…...
)
phpmyadmin 文件包含(CVE-2014-8959)
0x01 漏洞介绍 phpMyAdmin是phpMyAdmin团队开发的一套免费的、基于Web的MySQL数据库管理工具。该工具能够创建和删除数据库,创建、删除、修改数据库表,执行SQL脚本命令等。phpMyAdmin的GIS编辑器中libraries/gis/GIS_Factory.class.php脚本存在目录遍历漏洞。远程攻击者可借助…...

SpringBoot集成MyBatis
目录 实现步骤 1. 在项目的 pom.xml 配置文件中引入如下依赖 2. 在项目的 application.properties 配置文件中添加如下依赖 3. 新建 UserMapper.class 接口类,添加如下 3 个方法 4. 在 /resources/mybatis/mapper 路径(需要手动创建文件夹)下创建 UserMapper.xm…...

MySQL-索引
索引介绍索引是对数据库表中一列或者多列的值进行排序的一种结构,使用索引可提高数据库中特定数据的查询速度。索引是一个单独的、存储在磁盘上的数据库结构,它们包含着对数据表里所有记录的引用指针。使用索引用于快速找出在某个或多个列中有一特定值得…...

【STM32存储器映射-寄存器基地址-偏移】
前言 在学习STM32的时候,我们看到很多的寄存器编程, 比方说LED灯: //GPIOB.5端口输出高电平GPIOB->ODR|1<<5; //PB.5 输出高GPIOE->ODR|1<<5; //PE.5输出高 //GPIOB端口全部输出高电平*(unsigned int*)(0x4001 …...

【华为OD机试2023】最多颜色的车辆 C++ Java Python
【华为OD机试2023】最多颜色的车辆 C++ Java Python 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收…...
)
特斯拉后端面试(部分)
HR告知如果面试通过要转.net-_- round1 有没有用过Java新版本,知道有哪些特性吗?A:没有。Q:我们基本在用JDK11,有的新项目用到JDK17了。参考答案1: ZGC: A Scalable Low-Latency Garbage Collector Epsi…...
【python】使用python将360个文件夹里的照片,全部复制到指定的文件夹中,并且按照顺序重新命名
最近要做一个图像生成的课题,在网上找了一个混合的数据集。这个数据集中一共有360个文件夹,然后文件夹中有6-9张不等的照片,我的目标就是编写python代码将所有的照片取出来,放到一个指定的文件夹里,并且从1开始按照顺序…...

【C语言】3天速刷C语言(初识)
【声明】本篇博客只用于对与刚学习C语言的同学的一个初始了解,具体内容请继续关注本专栏后续内容。什么是C语言C语言是一门通用计算机编程语言,广泛应用于底层开发。C语言的设计目标是提供一种能以简易的方式编译、处理低级存储器、产生少量的机器码以及…...
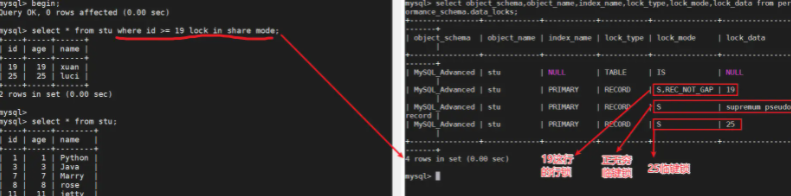
如何搞定MySQL锁(全局锁、表级锁、行级锁)?这篇文章告诉你答案!太TMD详细了!!!
概述 锁是计算机协调多个进程或线程并发访问某一资源的机制。在数据库中,除传统的计算资源(CPU、RAM、I/O)的争用以外,数据也是一种供许多用户共享的资源。如何保证数据并发访问的一致性、有效性是所有数据库必须解决的一个问题&…...

云计算生态该怎么做?阿里云计算巢打了个样
2023 年 2 月 23 日至 24 日,由阿里云主办的「阿里云计算巢加速器」于杭州阿里云谷园区集结。 阿里云计算巢加速器于 2022 年 8 月正式启动招募,最终百奥利盟、极智嘉、EMQ、KodeRover、MemVerge 等 30 家创新企业入选计算加速器,覆盖了人工智…...

小樽C++ 多章⑧ (贰) 指针与数组
目录 1.C中数组变量名某些情况可以看成是指针 2.C语言的scanf 输入语句,printf 输出语句 3.用指针来当动态数组 小樽C 多章⑧ (壹) 指针变量https://blog.csdn.net/weixin_44775255/article/details/129031168 小樽C 多章⑧ (叁) 指针与字符串、(肆) 函数与指针…...
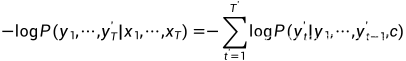
MXNet的机器翻译实践《编码器-解码器(seq2seq)和注意力机制》
机器翻译就是将一种语言翻译成另外一种语言,输入和输出的长度都是不定长的,所以这里会主要介绍两种应用,编码器-解码器以及注意力机制。编码器是用来分析输入序列,解码器用来生成输出序列。其中在训练时,我们会使用一些…...

RK3588平台开发系列讲解(同步与互斥篇)自旋锁介绍
平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 一、自旋锁介绍二、自旋锁相关的函数1、普通场景2、进程上下文和下半部3、中断相关三、相关结构体四、函数实现1、初始化2、获取自旋锁沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇介绍自旋锁的使用和基…...

Linux系统CPU占用率较高问题排查思路
作为工程师,在日常工作中我们会遇到 Linux服务器上出现CPU负载达到100%居高不下的情况,如果CPU 持续跑高,则会影响业务系统的正常运行,带来企业损失。对于CPU过载问题通常使用以下两种方式即可快速定位:方法一第一步&a…...
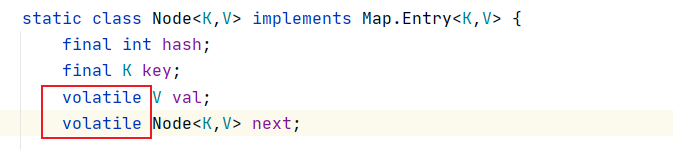
源码解析——HashMap
源码解析——HashMap1. 什么 是HashMap2. 为什么要使用HashMap3. HashMap的使用4. 源码解析4.1 关键问题4.1 存储结构4.2 HashMap 的容量和负载因子4.3 初始化过程4.3 put() 方法实现原理4.3.1 hash()4.3.2 resize()4.4 get() 方法实现原理5. 面试题总结6. ConcurrentHashmap(J…...

Elasticsearch 核心技术(六):内置的 8 种分词器详解 + 代码示例
❤️ 博客主页:水滴技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 🌸 订阅专栏:大数据核心技术从入门到精通 文章目录一、内置分词器1. Standard(标准分词器)英文示例中文示例…...

Mysql8.0的特性
Mysql8.0的特性 建议使用8.0.17及之后的版本,更新的内容比较多。 新增降序索引 -- 如下所示,我们可以在创建索引时 在字段名后面指定desc进行降序排序 create table t1(c1 int,c2 int,index idx_c1_c2(c1,c2 desc));group by 不再隐式排序 mysql5.7的版…...
JDK动态代理(tedu)(内含源代码)
JDK动态代理(tedu)(内含源代码) 源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87546187 目录JDK动态代理(tedu)(内含源代码)源代码下载链接…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
