LeetCode 454.四数相加II
LeetCode 454.四数相加II
1、题目
题目链接:454. 四数相加 II - 力扣(LeetCode)
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
- 0 <= i, j, k, l < n
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例 2:
输入:nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出:1
提示:
- n == nums1.length
- n == nums2.length
- n == nums3.length
- n == nums4.length
- 1 <= n <= 200
- -228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228
2、哈希法
代码
class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) { // key: a + b的数值,value: a + b数值出现的次数unordered_map<int, int> towSumMap; // 遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到 map 中for (int a : nums1) { for (int b : nums2) { ++towSumMap[a + b]; } } int count = 0; int s = 0; // 统计 a + b + c + d = 0 出现的次数for (int c : nums3) { for (int d : nums4) { s = 0 - c - d; // 检查这个相反数是否在映射中出现过。如果出现过,则将对应的出现次数累加到计数器上。 if (towSumMap.find(s) != towSumMap.end()) { count += towSumMap[s]; } } } // 返回计数器的值,即满足条件的元组的数量。 return count; }
};
复杂度分析
-
时间复杂度: O(n^2)
-
空间复杂度: O(n^2),最坏情况下A和B的值各不相同,值的个数为 n2,也就需要O(n2)的空间。
相关文章:

LeetCode 454.四数相加II
LeetCode 454.四数相加II 1、题目 题目链接:454. 四数相加 II - 力扣(LeetCode) 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 <…...
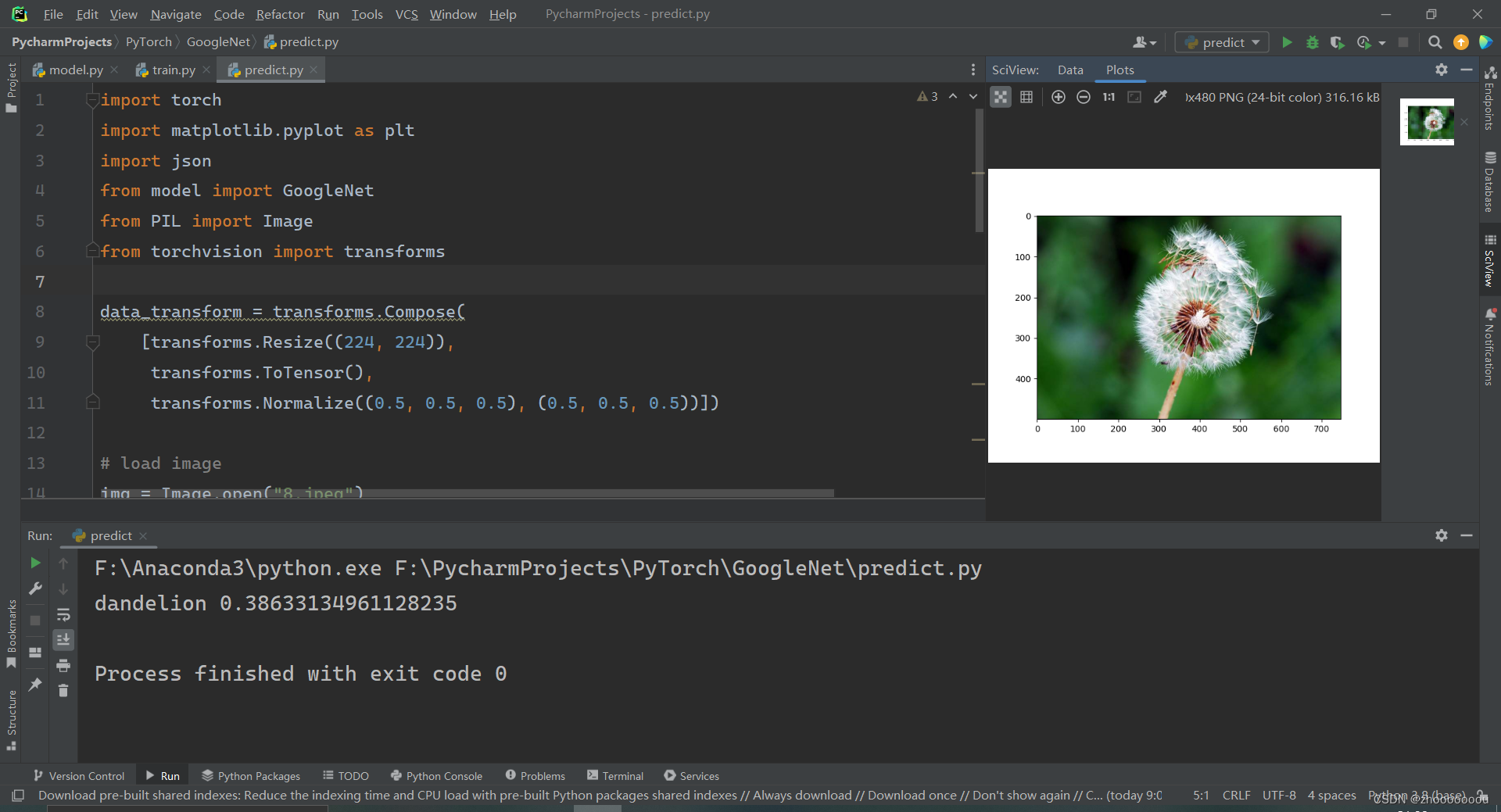
GoogleNet网络训练集和测试集搭建
测试集和训练集都是在之前搭建好的基础上进行修改的,重点记录与之前不同的代码。 还是使用的花分类的数据集进行训练和测试的。 一、训练集 1、搭建网络 设置参数:使用辅助分类器,采用权重初始化 net GoogleNet(num_classes5, aux_logi…...
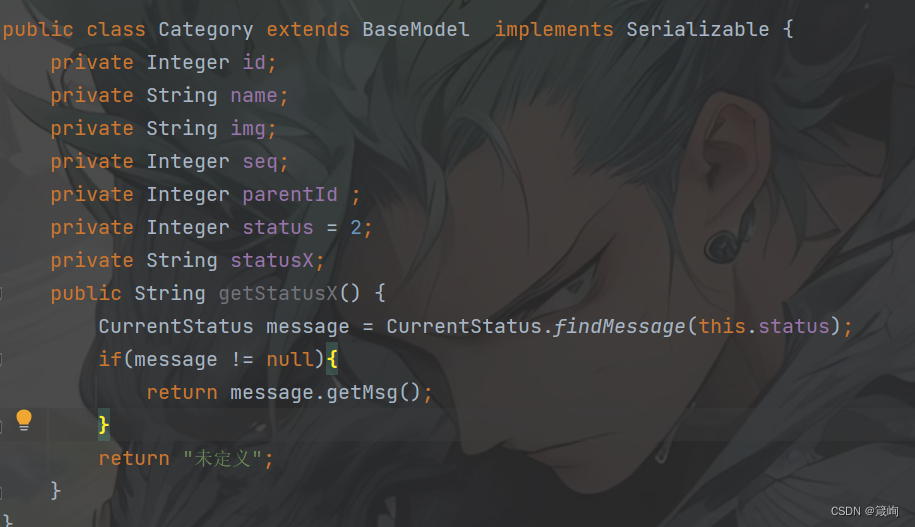
将数字状态码在后台转换为中文状态
这是我们的实体类 可以看出我们的状态status是2如过返回到前端我们根本不知道2代表的是什么,所以我们需要再这里将数字转换成能看懂的中文状态,首先我们创建一个枚举类 先将我们状态码所对应的中文状态枚举出来,然后创建一个静态方法&#…...

2017NOIP普及组真题 4. 跳房子
线上OJ: 一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid1417\ 核心思想 首先、本题中提到 “ 至少 要花多少金币改造机器人,能获得 至少 k分 ”。看到这样的话语,基本可以考虑要使用 二分答案。 那么,本题中…...

网络与 Internet因特网的基本概念
目录 网络Internet (互联网或互连网)Internet(因特网)待续、更新中 网络 指将分布在不同地理位置的、相同或不同类型的网络通过网络互连设备(中继器、网桥、路由器或网关等)相互连接,形成一个范…...

vue-router 中 router-link 与 a 标签的区别
文章目录 前言 a标签定义 router-link定义 总结 前言 vue-router 中 router-link 与 a 标签的区别 a标签定义 <a> 标签定义超链接,用于从一张页面链接到另一张页面。 从一张页面跳转到另一张页面,但从这里来说就违背了多视图的单页Web应用这个…...
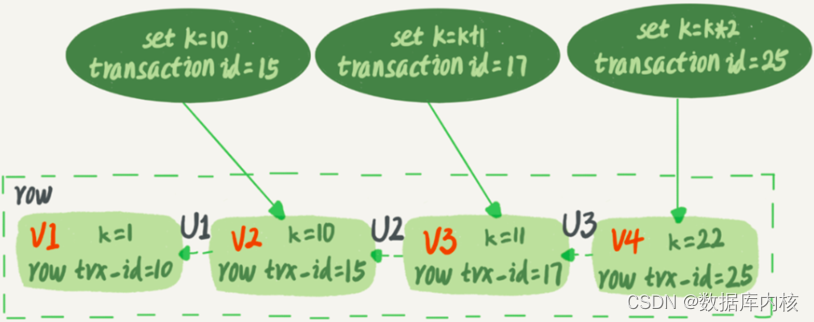
MySQL基础知识——MySQL事务
事务背景 什么是事务? 一组由一个或多个数据库操作组成的操作组,能够原子的执行,且事务间相互独立; 简单来说,事务就是要保证一组数据库操作,要么全部成功,要么全部失败。 注:MyS…...

【架构方法论(一)】架构的定义与架构要解决的问题
文章目录 一. 架构定义与架构的作用1. 系统与子系统2. 模块与组件3. 框架与架构4. 重新定义架构:4R 架构 二、架构设计的真正目的-别掉入架构设计的误区1. 是为了解决软件复杂度2. 简单的复杂度分析案例 三. 案例思考 本文关键字 架构定义 架构与系统的关系从业务逻…...
基于springboot实现人口老龄化社区服务与管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现人口老龄化社区服务与管理系统演示 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了人口老龄化社区服务与管理平台的开发全过程。通过分析人口老龄化社区服务与管理平台方面的不足ÿ…...
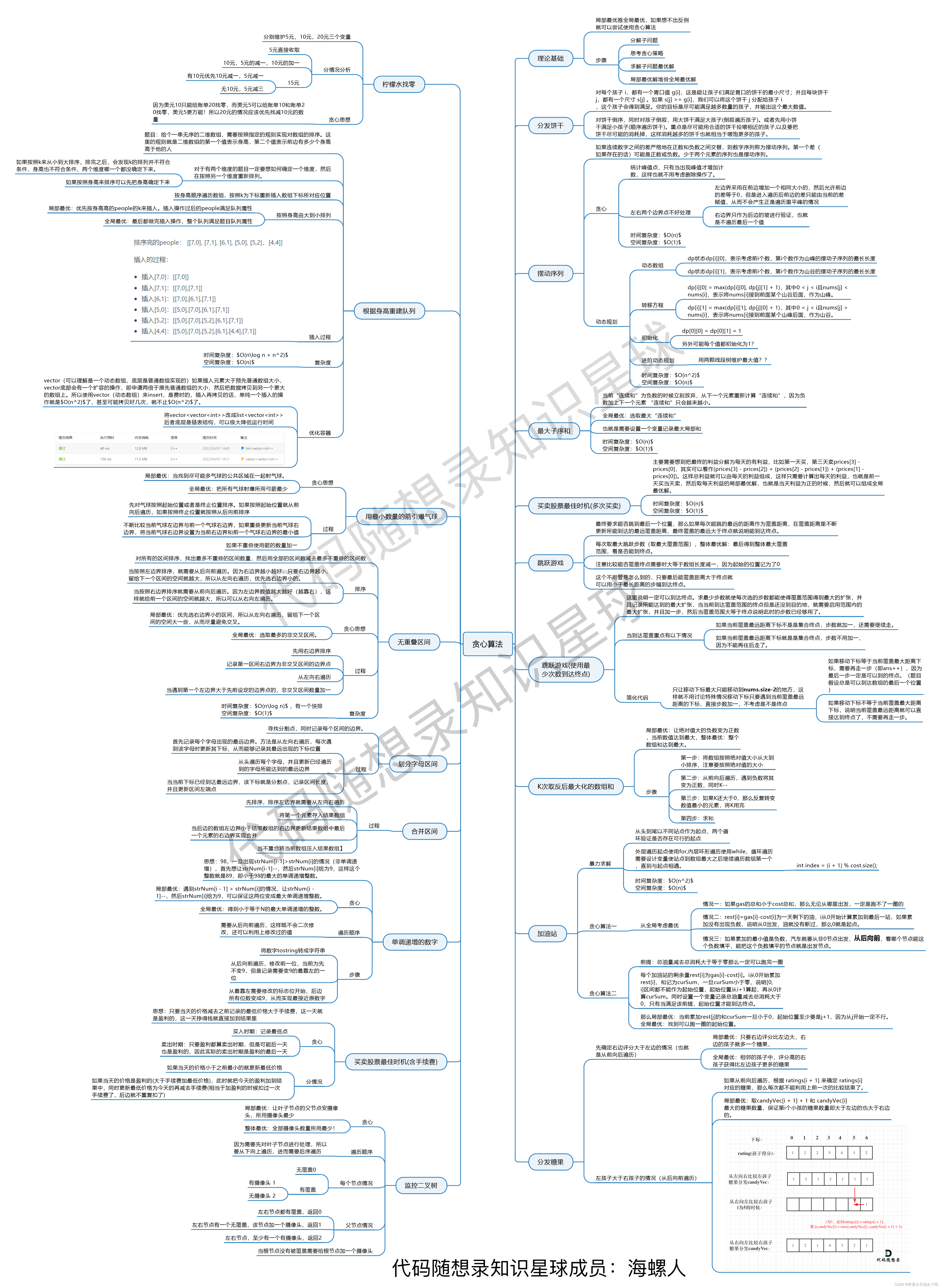
代码随想录算法训练营第三十七天| LeetCode 738.单调递增的数字、总结
一、LeetCode 738.单调递增的数字 题目链接/文章讲解/视频讲解:https://programmercarl.com/0738.%E5%8D%95%E8%B0%83%E9%80%92%E5%A2%9E%E7%9A%84%E6%95%B0%E5%AD%97.html 状态:已解决 1.思路 如何求得小于等于N的最大单调递增的整数?98&am…...

C++动态内存管理 解剖new/delete详细讲解(operator new,operator delete)
讨厌抄我作业和不让我抄作业的人 讨厌插队和不让我插队的人 讨厌用我东西和不让我用东西的人 讨厌借我钱和不借给我钱的人 讨厌开车加塞和不让我加塞的人 讨厌内卷和打扰我内卷的人 一、C中动态内存管理 1.new和delete操作内置类型 2.new和delete操作自定义类型 二、operat…...

python-re正则笔记0.2.0
1. 匹配linux文件路径 from re import match, search,findall str"sh refreshConfig.sh /opt/client/ccc.txt /opt/client/ccc.dfs 胜多负少的"patter1"\/.\.\w" print(findall(patter1, str))""" [/opt/client/ccc.txt /opt/client/ccc…...
.NET SignalR Redis实时Web应用
环境 Win10 VS2022 .NET8 Docker Redis 前言 什么是 SignalR? ASP.NET Core SignalR 是一个开放源代码库,可用于简化向应用添加实时 Web 功能。 实时 Web 功能使服务器端代码能够将内容推送到客户端。 适合 SignalR 的候选项: 需要从服…...

【热门话题】常见分类算法解析
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 常见分类算法解析1. 逻辑回归(Logistic Regression)2. 朴…...

有效利用MRP能为中小企业带来什么?
在离散制造企业,主流的生产模式主要为面向订单生产和面向库存生产(又称为预测生产),在中小企业中,一般为面向订单生产,也有部分面向库存和面向订单混合的生产方式(以面向订单为主,面…...

InternlM2
第一次作业 基础作业 进阶作业 1. hugging face下载 2. 部署 首先,从github上git clone仓库 https://github.com/InternLM/InternLM-XComposer.git然后里面的指引安装环境...

2024-12.python高级语法
异常处理 首先我们要理解什么叫做**"异常”**? 在程序运行过程中,总会遇到各种各样的问题和错误。有些错误是我们编写代码时自己造成的: 比如语法错误、调用错误,甚至逻辑错误。 还有一些错误,则是不可预料的错误…...
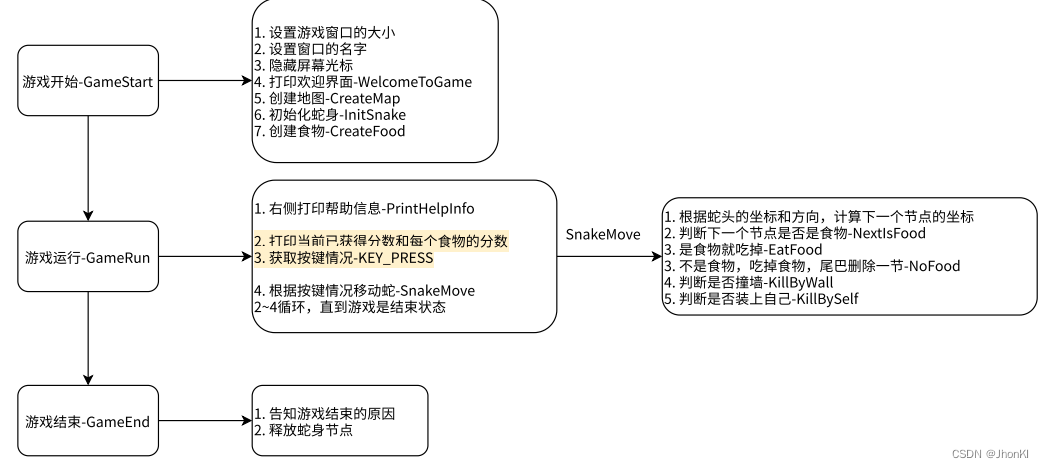
【C语言】贪吃蛇项目(1) - 部分Win32 API详解 及 贪吃蛇项目思路
文章目录 一、贪吃蛇项目需要实现的基本功能二、Win32 API介绍2.1 控制台2.2 部分控制台命令及调用函数mode 和 title 命令COORD 命令GetStdHandle(获取数据)GetConsoleCursorInfo(获取光标数据)SetConsoleCursorInfo (…...

秋叶Stable diffusion的创世工具安装-带安装包链接
来自B站up秋葉aaaki,近期发布了Stable Diffusion整合包v4.7版本,一键在本地部署Stable Diffusion!! 适用于零基础想要使用AI绘画的小伙伴~本整合包支持SDXL,预装多种必须模型。无需安装git、python、cuda等任何内容&am…...
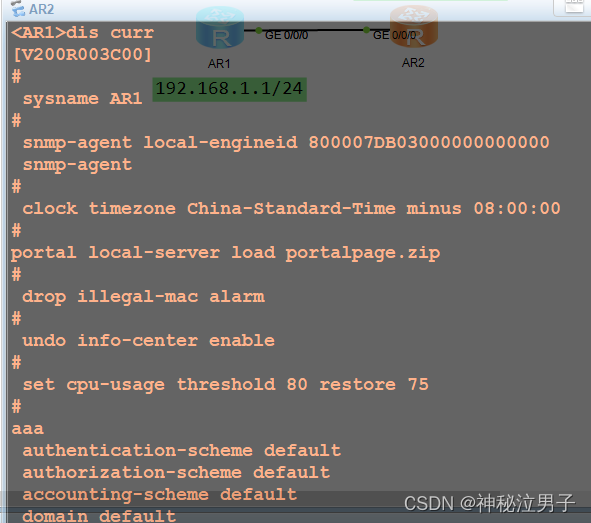
华为ensp中aaa(3a)实现telnet远程连接认证配置命令
作者主页:点击! ENSP专栏:点击! 创作时间:2024年4月14日18点49分 AAA认证的全称是Authentication、Authorization、Accounting,中文意思是认证、授权、计费。 以下是详细解释 认证(Authentic…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
