第十五届蓝桥杯复盘python大学A组——试题B 召唤数学精灵

按照正常思路解决,由于累乘消耗大量时间,因此这不是一个明智的解决方案。
这段代码执行速度非常慢的原因在于它试图计算非常大的数的阶乘(累乘),并且对于每一个i的值都执行这个计算。阶乘的增长是极其迅速的,即使对于相对较小的i值,结果也会迅速超出Python标准整数类型的表示范围。此外,代码中的count变量应该被定义在循环外部,否则它会在每次迭代中重置为0。
另外,即使a和b的计算都在整数范围内进行(使用了//进行整数除法),但b=B(i)这一步仍然是非常耗时的,因为它涉及到大量的乘法运算,并且这些运算的结果会迅速增大。
使用C++等编译型语言可能会在一定程度上提高执行速度,因为编译型语言通常具有更好的性能优化。C++等语言允许更底层的内存管理和更精细的控制结构,这可以减少一些Python解释和执行代码时的开销。此外,C++标准库和第三方库可能提供了针对大数运算的优化算法和数据结构。
但是,即使使用C++,如果算法本身没有改进(即仍然试图计算巨大的阶乘),那么性能提升也可能是有限的。对于阶乘这样快速增长的函数,无论使用哪种语言,都会很快遇到数值表示的限制。
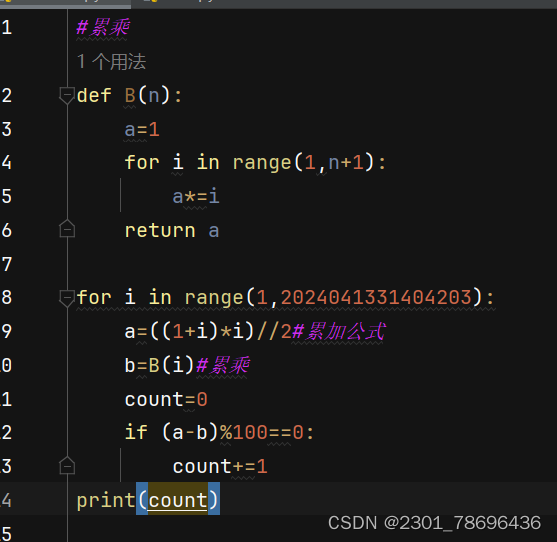
改进
由于这是一个巨大的数据量,因此要找规律
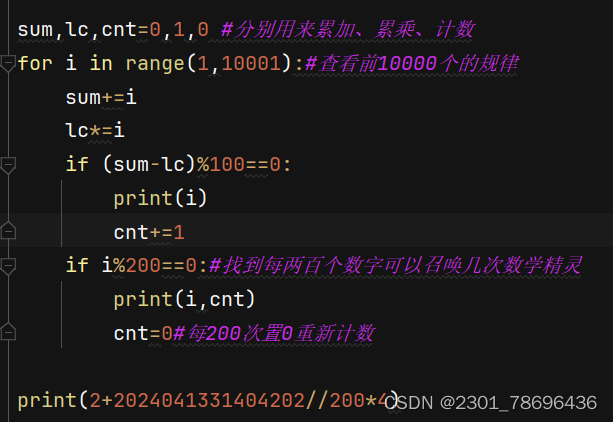
部分结果
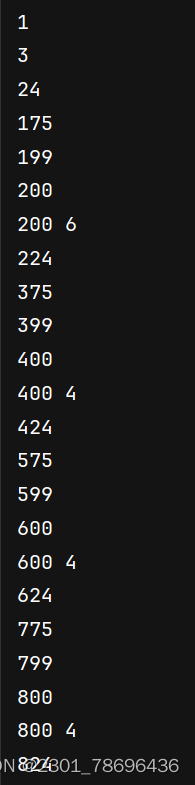
最终结果
相关文章:

第十五届蓝桥杯复盘python大学A组——试题B 召唤数学精灵
按照正常思路解决,由于累乘消耗大量时间,因此这不是一个明智的解决方案。 这段代码执行速度非常慢的原因在于它试图计算非常大的数的阶乘(累乘),并且对于每一个i的值都执行这个计算。阶乘的增长是极其迅速的ÿ…...

网络通信——常见结构及强联网游戏和弱联网游戏区别
声明:本文为个人笔记,用于学习研究使用非商用,内容为个人研究及综合整理所得,若有违规,请联系,违规必改。 网络通信——常见结构及强联网游戏和弱联网游戏区别 文章目录 网络通信——常见结构及强联网游戏和…...

如何安装PyFluent
0.什么是PyFluent? 官方介绍如下: PyFluent 是 PyAnsys 生态系统的一部分, 允许您在所选的 Python 环境中结合使用 Fluent 与其他 PyAnsys 库和外部 Python 库一起使用。 PyFluent 实现了客户端-服务器体系结构。它使用谷歌遥控器 过程调用或 gRPC 接…...

Qt 2 QMapQHashQVector类实例
1. QMap // 1:QMap的使用// 创建一个QMap 实例 key 为 QString value 为 intQMap<QString,int> Grade;// 插入方式有两种插入方式// 1.map[key] valueGrade["语文"] 90;Grade["数学"] 120;// 2.map.insert(key,value);Grade.insert("英语&qu…...

使用Git将文件夹上传到Github以及使用Git LFS上传大文件
使用Git将文件夹上传到Github以及使用Git LFS上传大文件...
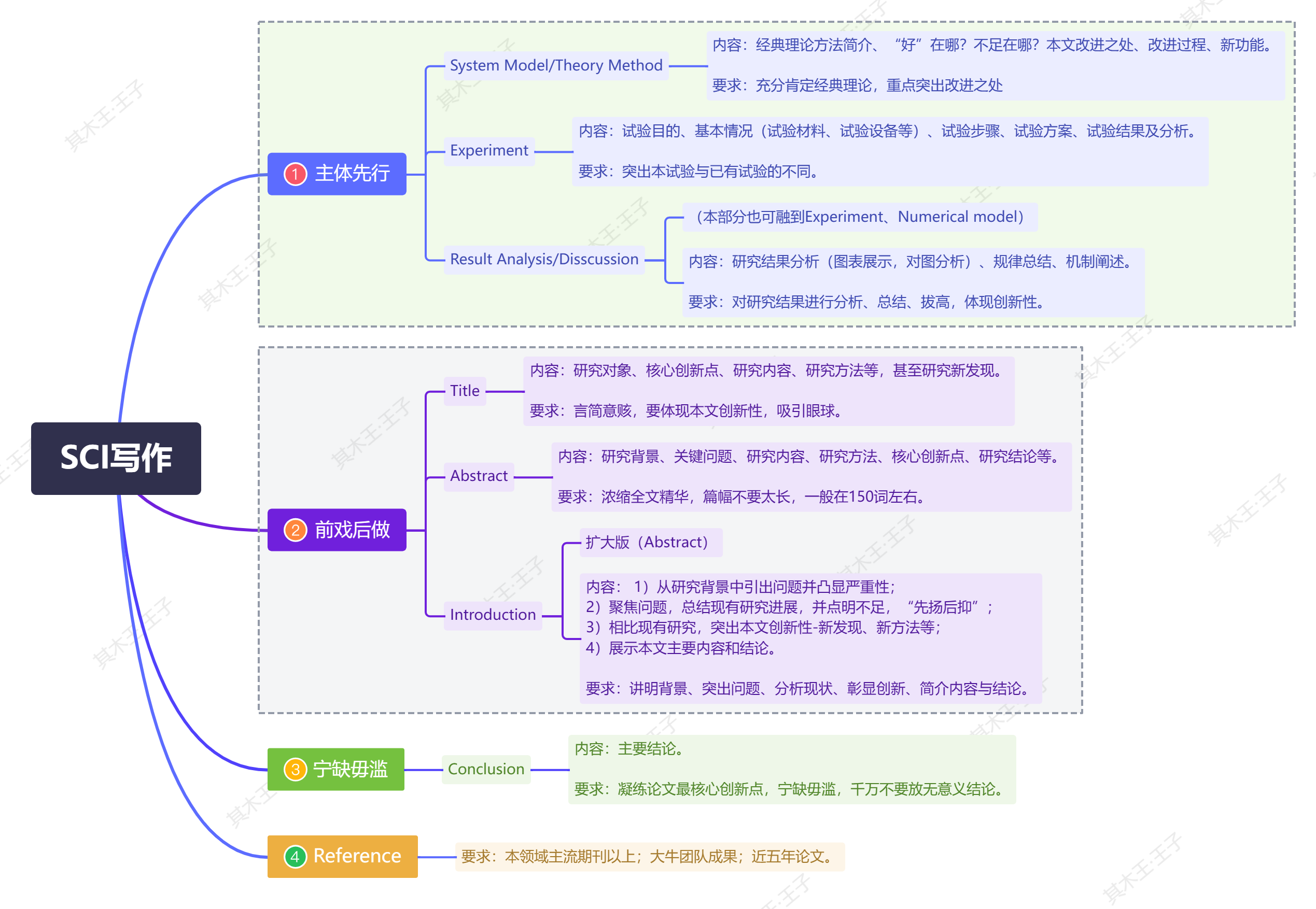
1.SCI各模块
1.学会“抄” 写论文,一定要学会“抄”!这样才能事半功倍,尤其是对于初次写作的新手,否则写作过程一定会让你痛不欲生,而且写出来的东西就是一坨shi,不仅折磨自己,也折磨导师。 写论文与建大楼…...
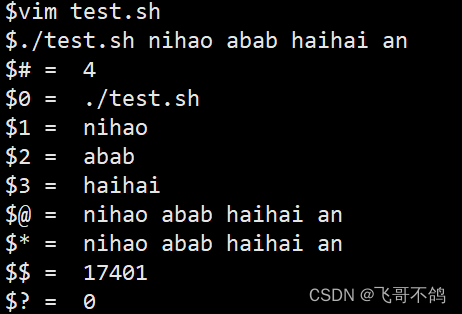
记录shell编程中$1,$@等符号的含义
笔者最近老是遇到shell中的$相关的题目,于是打算写篇文章记录一下。考虑到并没有特别多需要解释的内容,所以并不会进行介绍,上图上表上代码,让机器说话,machine always right test.sh #/bin/bash echo $# $# echo …...
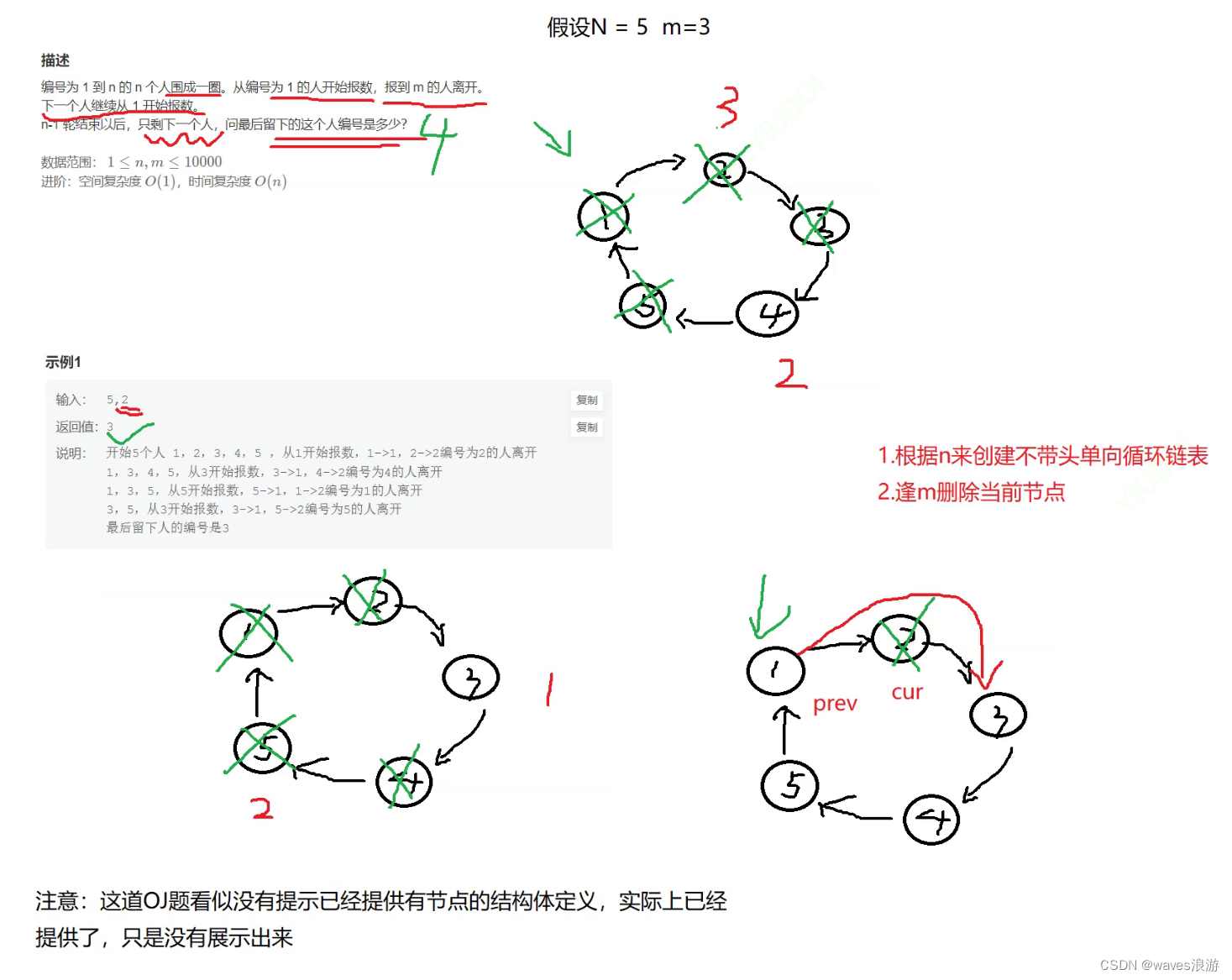
单链表的应用
文章目录 目录1. 单链表经典算法OJ题目1.1 [移除链表元素](https://leetcode.cn/problems/remove-linked-list-elements/description/)1.2 [链表的中间节点](https://leetcode.cn/problems/middle-of-the-linked-list/description/)1.3 [反转链表](https://leetcode.cn/problem…...

手机副业赚钱秘籍:让你的手机变成赚钱利器
当今社会,智能手机已然成为我们生活不可或缺的一部分。随着技术的飞速进步,手机不再仅仅是通讯工具,而是化身为生活伴侣与工作助手。在这个信息爆炸的时代,我们时常会被一种焦虑感所困扰:如何能让手机超越消磨时光的定…...
Flask之数据库连接池DBUtils库)
(二十七)Flask之数据库连接池DBUtils库
目录: 每篇前言:DBUtils库模式一(底层使用threading.local实现):模式二:Flask中使用方式一:直接将DBUtils初始化放到settings.py文件中方式二:从utils文件夹中导入脚本使用DBUtils代码demo:每篇前言: 🏆🏆作者介绍:【孤寒者】—CSDN全栈领域优质创作者、HDZ核心…...

FewShotPromptTemplate和SemanticSimilarityExampleSelector的学习
FewShotPromptTemplate 和 SemanticSimilarityExampleSelector 是在少样本学习(FewShot Learning)场景中常用的两种技术,它们在提高模型泛化能力和减少对大量标注数据的依赖方面扮演着重要角色。 下面我会解释它们之间的关系: F…...

【保姆级】2024年OnlyFans订阅指南
OnlyFans是一个独特的社交媒体平台,它为创作者和粉丝提供了一个互动交流的空间。通过这个平台,创作者可以分享他们的独家内容,而粉丝则可以通过订阅来支持和享受这些内容。如果你对OnlyFans感兴趣,并希望成为其中的一员࿰…...

深入理解JVM中的G1垃圾收集器原理、过程和参数配置
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 在Java虚拟机(JVM)中,垃圾收集(GC)是一个自动管理内存的过程ÿ…...
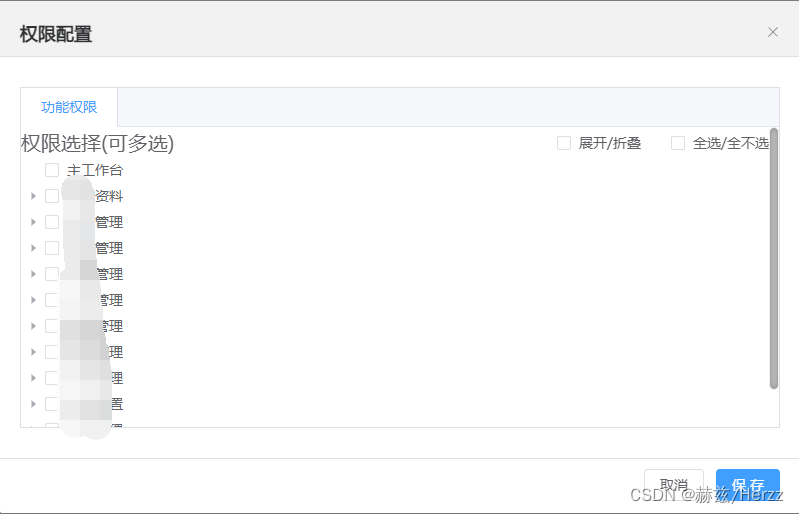
VUE3 + Elementui-Plus 之 树形组件el-tree 一键展开(收起);一键全选(不全选)
需求: 产品要求权限树形结构添加外部复选框进行全部展开或收起;全选或不全选。 实现步骤: tree组件部分: <div class"role-handle"><div>权限选择(可多选)</div><div><el-checkbox v-mode…...
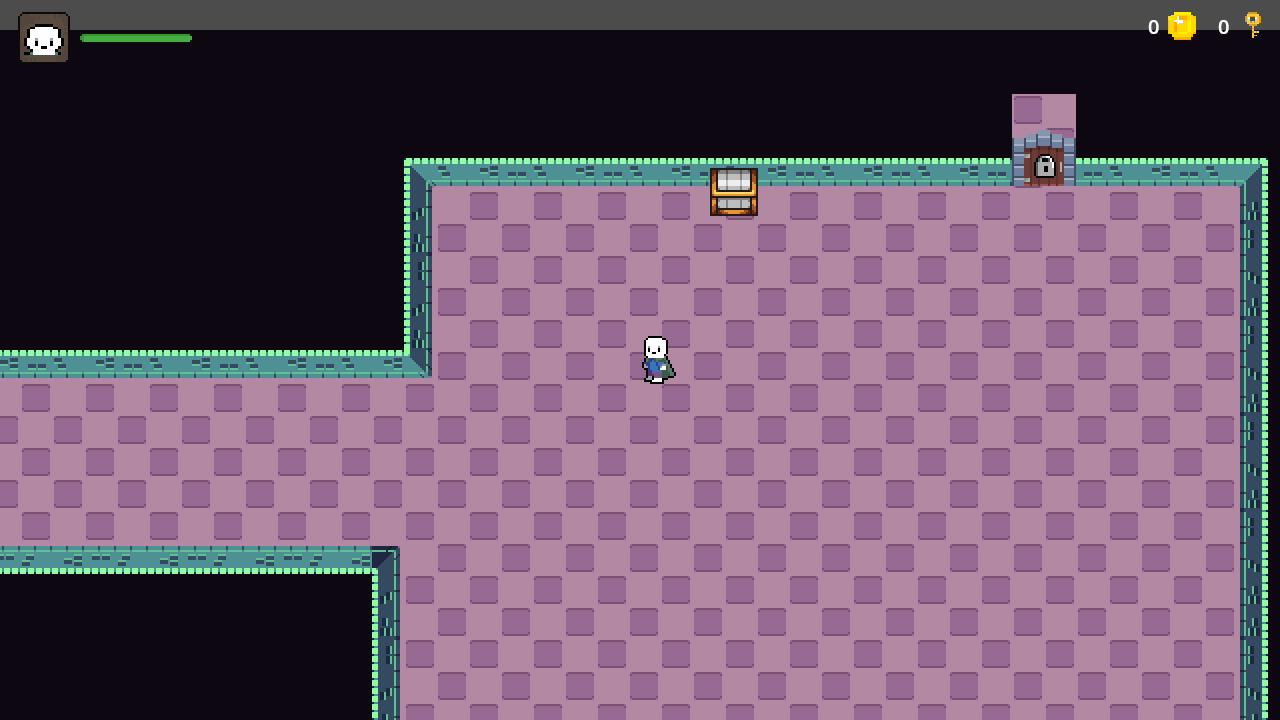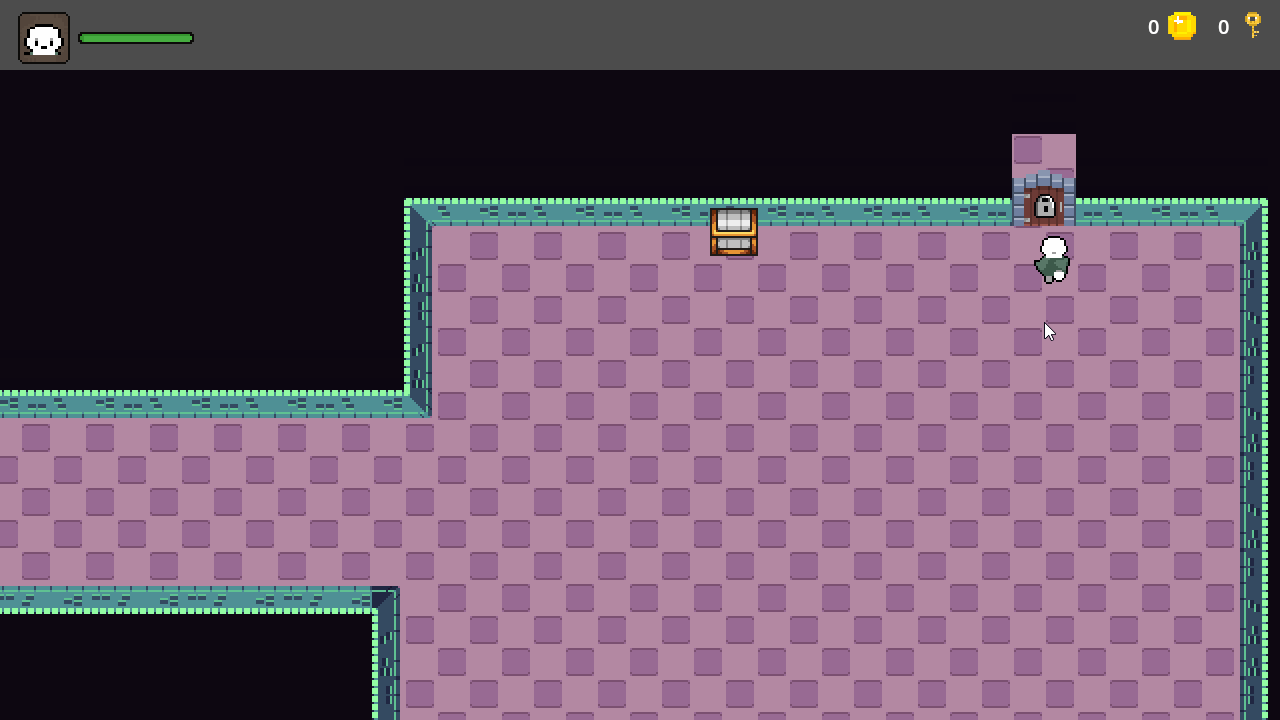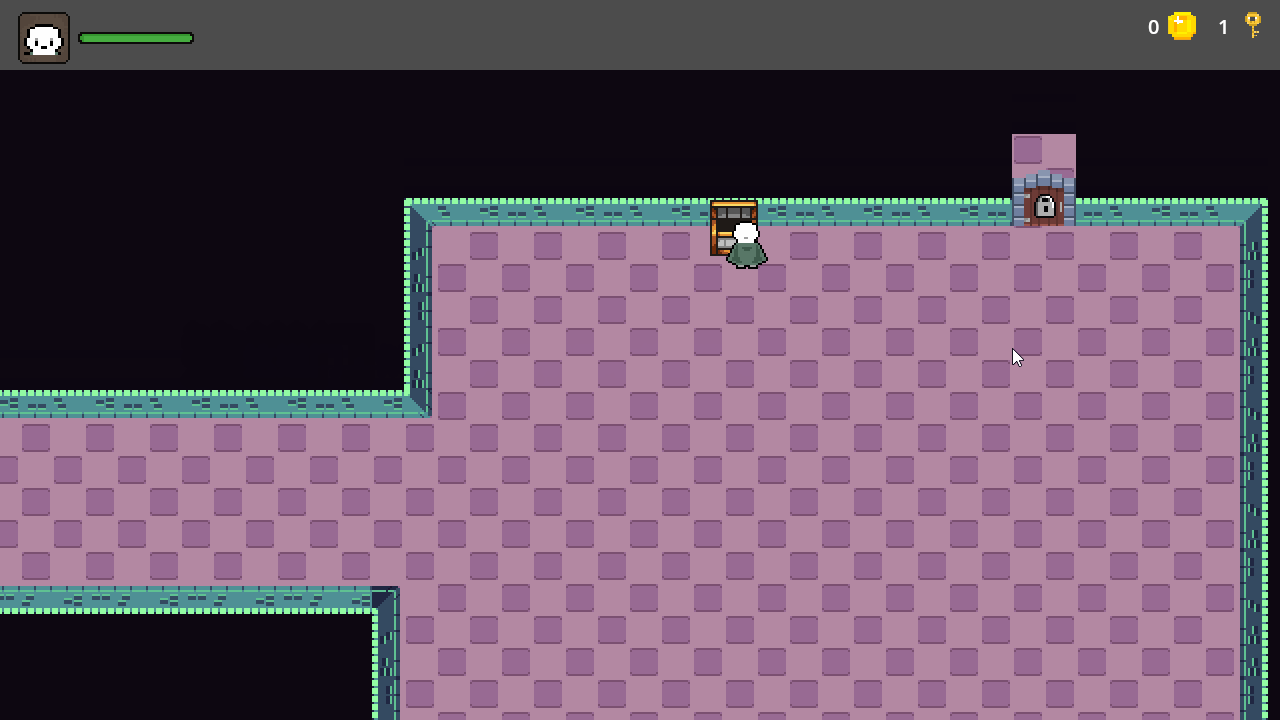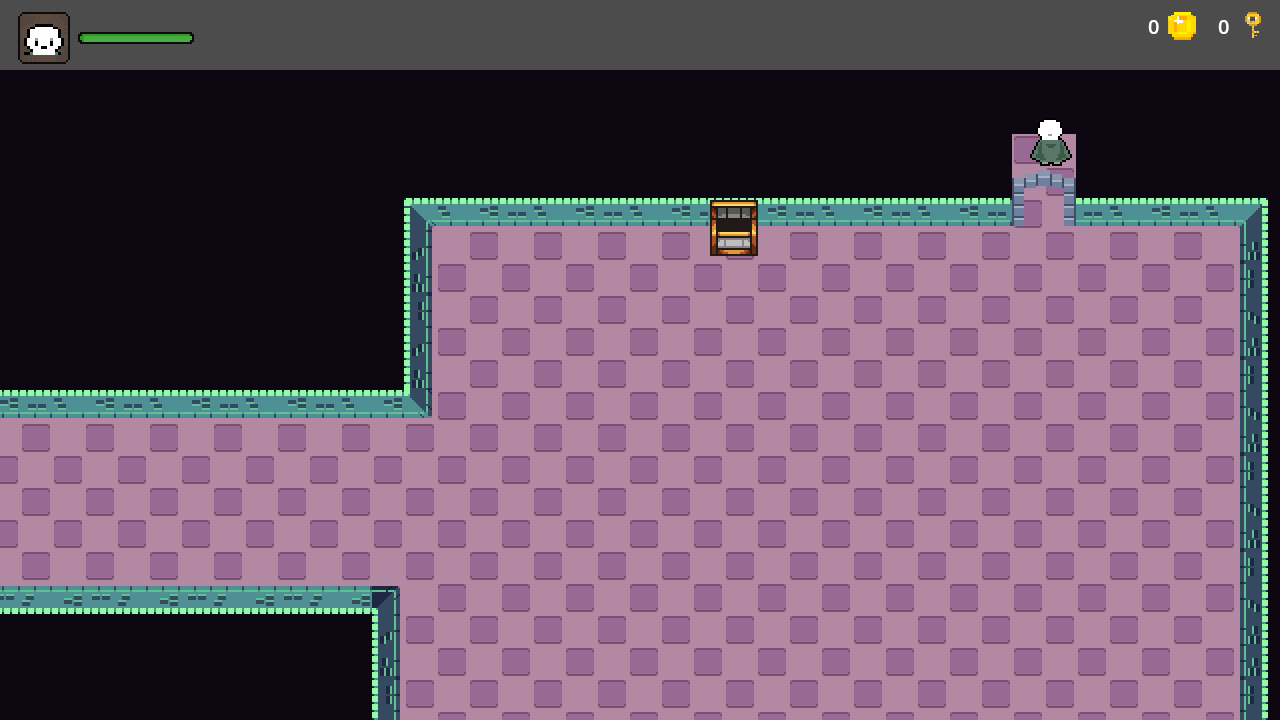
【Godot4自学手册】第三十七节钥匙控制开门
有些日子没有更新了,实在是琐事缠身啊,今天继续开始自学Godot4,继续完善地宫相关功能,在地宫中安装第二道门,只有主人公拿到钥匙才能开启这扇门,所以我们在合适位置放置一个宝箱,主人公开启宝箱…...

GitHub repository - Pulse - Contributors - Network
GitHub repository - Pulse - Contributors - Network 1. Pulse2. Contributors3. NetworkReferences 1. Pulse 显示该仓库最近的活动信息。该仓库中的软件是无人问津,还是在火热地开发之中,从这里可以一目了然。 2. Contributors 显示对该仓库进行过…...
RocketMQ 10 面试题FAQ
RocketMQ 面试FAQ 说说你们公司线上生产环境用的是什么消息中间件? 为什么要使用MQ? 因为项目比较大,做了分布式系统,所有远程服务调用请求都是同步执行经常出问题,所以引入了mq 解耦 系统耦合度降低,没有强依赖…...

【Spring进阶系列丨第十篇】基于注解的面向切面编程(AOP)详解
文章目录 一、基于注解的AOP1、配置Spring环境2、在beans.xml文件中定义AOP约束3、定义记录日志的类【切面】4、定义Bean5、在主配置文件中配置扫描的包6、在主配置文件中去开启AOP的注解支持7、测试8、优化改进9、总结 一、基于注解的AOP 1、配置Spring环境 <dependencie…...

Leetcode 152. 乘积最大子数组和Leetcode 162. 寻找峰值
文章目录 Leetcode 152. 乘积最大子数组题目描述C语言题解和思路解题思路 Leetcode 162. 寻找峰值题目描述C语言题解和思路解题思路 Leetcode 152. 乘积最大子数组 题目描述 给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中…...

项目实战之网络电话本之发送邮件名片和导出word版个人信息
1、项目介绍 1)项目功能 用户管理:分为管理员、和普通用户,设置不同用户的权限 电话本信息管理:支持管理员和普通用户对电话本的信息进行增删改操作,模糊查询(根据姓名、地址、单位) 文件批…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
