Leetcode 152. 乘积最大子数组和Leetcode 162. 寻找峰值
文章目录
- Leetcode 152. 乘积最大子数组
- 题目描述
- C语言题解和思路
- 解题思路
- Leetcode 162. 寻找峰值
- 题目描述
- C语言题解和思路
- 解题思路
Leetcode 152. 乘积最大子数组
题目描述
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
- 1 <= nums.length <= 2 * 10^4
- -10 <= nums[i] <= 10
- nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
C语言题解和思路
int maxProduct(int* nums, int numsSize) {int i, max = nums[0], min = nums[0], ret = nums[0];for(i = 1; i < numsSize; i++){if(nums[i] < 0){int tmp = max;max = min;min = tmp;}max = fmax(max * nums[i], nums[i]);min = fmin(min * nums[i], nums[i]);ret = fmax(ret, max);}return ret;
}
解题思路
动态规划
乘积的最大子数组和和求子数组最大的和不一样,两个很小的数相乘可能会变成最大的数(负负得正),所以我们不止要记录子数组最大的乘积,还要记录子数组最小的乘积。
将记录最大值的变量 max 、记录最小值的变量 min 、记录返回值的变量 ret ,全部初始化为数组 nums 的第一个数。
从数组的第二个数开始遍历数组,如果该数是负数,交换最大值和最小值。比较该数和最大值与该数的乘积,取更大大值,更新最大值;比较该数与最小值与该数的乘积,取更小值,更新最小值;比较返回值和最大值,更新返回值。
最后返回 ret 。
Leetcode 162. 寻找峰值
题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
- 1 <= nums.length <= 1000
- -231 <= nums[i] <= 231 - 1
- 对于所有有效的 i 都有 nums[i] != nums[i + 1]
C语言题解和思路
int findPeakElement(int* nums, int numsSize) {if(numsSize == 1){return 0;}int i = 1, max = 0;while(i + 1 < numsSize){if(nums[i - 1] < nums[i] && nums[i] > nums[i + 1]){return i;}max = nums[max] > nums[i] ? max : i;if(nums[i + 1] < nums[i]){i += 2;}else{i++;}}max = nums[max] > nums[numsSize - 1] ? max : numsSize - 1;return max;
}
解题思路
这题在寻找数组中的峰值元素,如果该元素大于左右两边的元素,直接返回该元素下标,如果不存在大于左右两边的元素,返回最大值元素的下标,所以在循环中,我们还同时要记录数组最大值元素的下标。
最大值下标初始化为 0 ,从下标 1 开始遍历数组:判断该下标的元素是否满足条件,如果满足,直接返回该下标;比较值和最大值,记录更大值的下标;判断该元素的下一个元素比该元素小还是大,如果比该元素小, i 前进两步,否则 i 前进一步。
如果循环结束还没有返回任何值,返回最大值的下标。
相关文章:

Leetcode 152. 乘积最大子数组和Leetcode 162. 寻找峰值
文章目录 Leetcode 152. 乘积最大子数组题目描述C语言题解和思路解题思路 Leetcode 162. 寻找峰值题目描述C语言题解和思路解题思路 Leetcode 152. 乘积最大子数组 题目描述 给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中…...

项目实战之网络电话本之发送邮件名片和导出word版个人信息
1、项目介绍 1)项目功能 用户管理:分为管理员、和普通用户,设置不同用户的权限 电话本信息管理:支持管理员和普通用户对电话本的信息进行增删改操作,模糊查询(根据姓名、地址、单位) 文件批…...

前端面试问题汇总 - HTTP篇
1. 登录拦截如何实现? 在前端,可以拦截所有需要登录的请求,如果用户未登录或者登录过期,则跳转到登录页面。 2. http 缓存有哪些? 强缓存: 强缓存是指在客户端请求资源时,先检查本地是否存在缓存…...

Java的IO流
Day35 Java的IO流 概念 Java的IO流是用来处理输入和输出操作的机制,用于在程序和外部数据源(如文件、网络连接、内存等)之间进行数据传输。Java的IO流主要分为字节流和字符流两种类型,每种类型又分为输入流和输出流。 理解&#…...

Node.js 中的 RSA 加密、解密、签名与验证详解
引言 在现代的网络通信中,数据安全显得尤为重要。RSA加密算法因其非对称的特性,广泛应用于数据的加密、解密、签名和验证等安全领域。本文将详细介绍RSA算法的基本原理,并结合Node.js环境,展示如何使用内置的crypto模块和第三方库…...
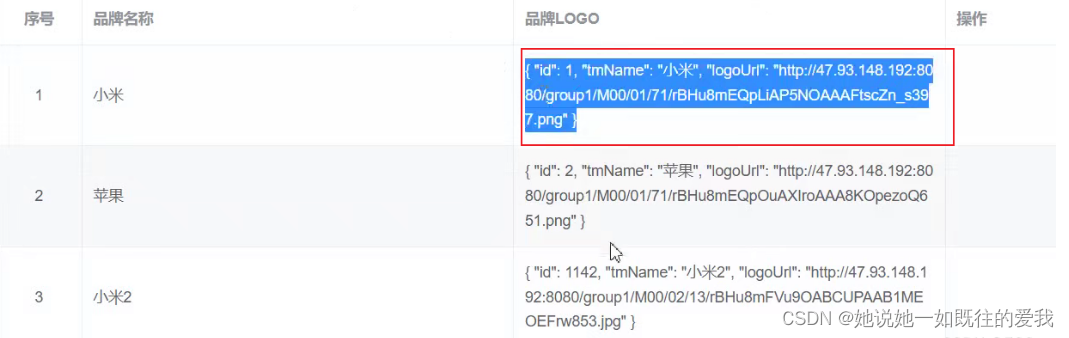
vue+element作用域插槽
作用域插槽的样式由父组件决定,内容却由子组件控制。 在el-table使用作用域插槽 <el-table><el-table-column slot-scope" { row, column, $index }"></el-table-column> </el-table>在el-tree使用作用域插槽 <el-tree>…...

MUSA模型
MUSA模型在软件可靠性工程中起到的作用是估计软件的故障/失效数量和故障率。具体来说,MUSA模型包括基本模型和对数模型。 MUSA基本模型假设故障发生的时间间隔服从参数为lambda的指数分布。在这个模型中,当故障被检测到时,发生故障的部分会被…...
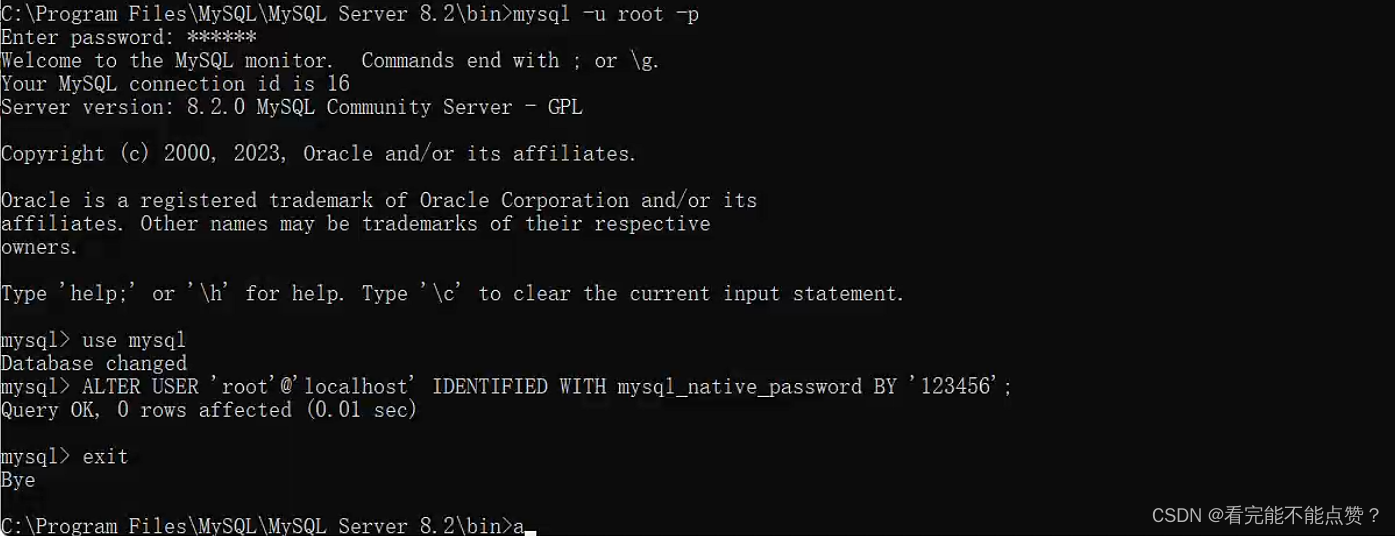
avicat连接异常,错误编号2059-authentication plugin…
错误原因为密码方式不对,具体可自行百度 首先管理员执行cmd进入 mysql安装目录 bin下边 我的是C:\Program Files\MySQL\MySQL Server 8.2\bin> 执行 mysql -u -root -p 然后输入密码 123456 进入mysql数据库 use mysql 执行 ALTER USER rootlocalhost IDE…...
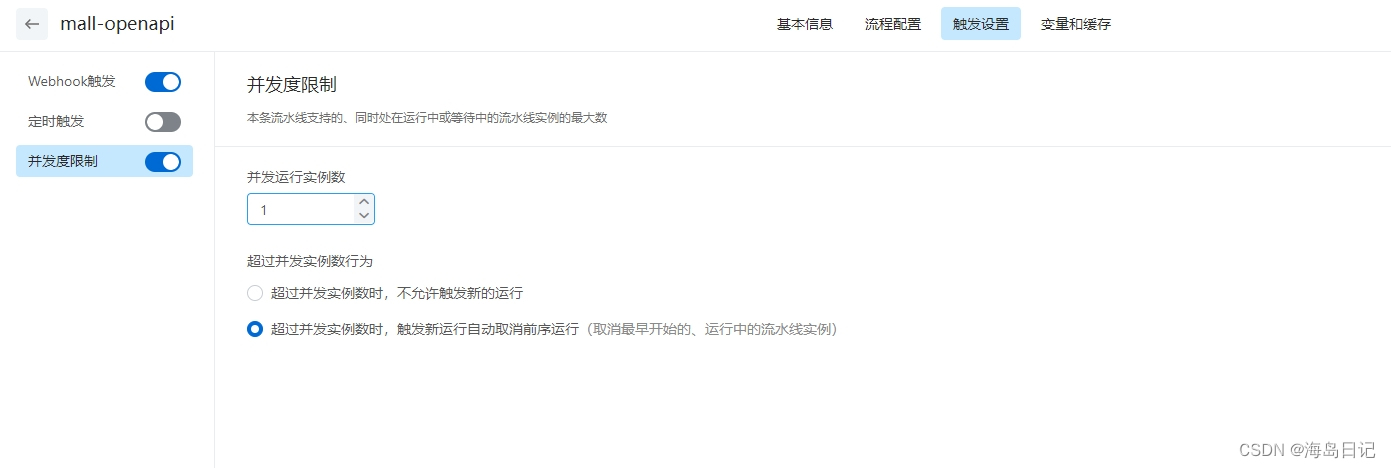
阿里云云效CI/CD配置
1.NODEJS项目流水线配置(vue举例) nodejs构建配置 官方教程 注意:下图的dist是vue项目打包目录名称,根据实际名称配置 # input your command here cnpm cache clean --force cnpm install cnpm run build 主机部署配置 rm -rf /home/vipcardmall/frontend/ mkdir -p /home/…...

个人开发者,Spring Boot 项目如何部署
今天给大家分享一下,作为个人开发者,Spring Boot 项目是如何部署的。 环境介绍 Linux docker docker-compose 目录结构 erwin-windrunner - backups - data - jars - build-docker-compose.sh - docker-compose.yml - Dockerfile文件 Dockerfile …...

【Spring进阶系列丨第九篇】基于XML的面向切面编程(AOP)详解
文章目录 一、基于XML的AOP1.1、打印日志案例1.1.1、beans.xml中添加aop的约束1.1.2、定义Bean 1.2、定义记录日志的类【切面】1.3、导入AOP的依赖1.4、主配置文件中配置AOP1.5、测试1.6、切入点表达式1.6.1、访问修饰符可以省略1.6.2、返回值可以使用通配符,表示任…...

学习记录:转发和重定向
转发(Forward)和重定向(Redirect)是两种不同的 Web 请求处理方式,它们在功能和行为上有着显著的区别。 区别 转发(Forward): 服务器内部跳转:转发是服务器内部的行为&…...
数据上云存储)
实现(图像、视频等)数据上云存储
实现(图像、视频等)数据上云存储 实现(图像、视频等)数据上云存储通常涉及以下几个步骤: 选择云存储服务商: 根据您的需求、预算、地域覆盖、数据安全性、服务稳定性等因素,选择一家合适的云存储…...

LeetCode 454.四数相加II
LeetCode 454.四数相加II 1、题目 题目链接:454. 四数相加 II - 力扣(LeetCode) 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 <…...
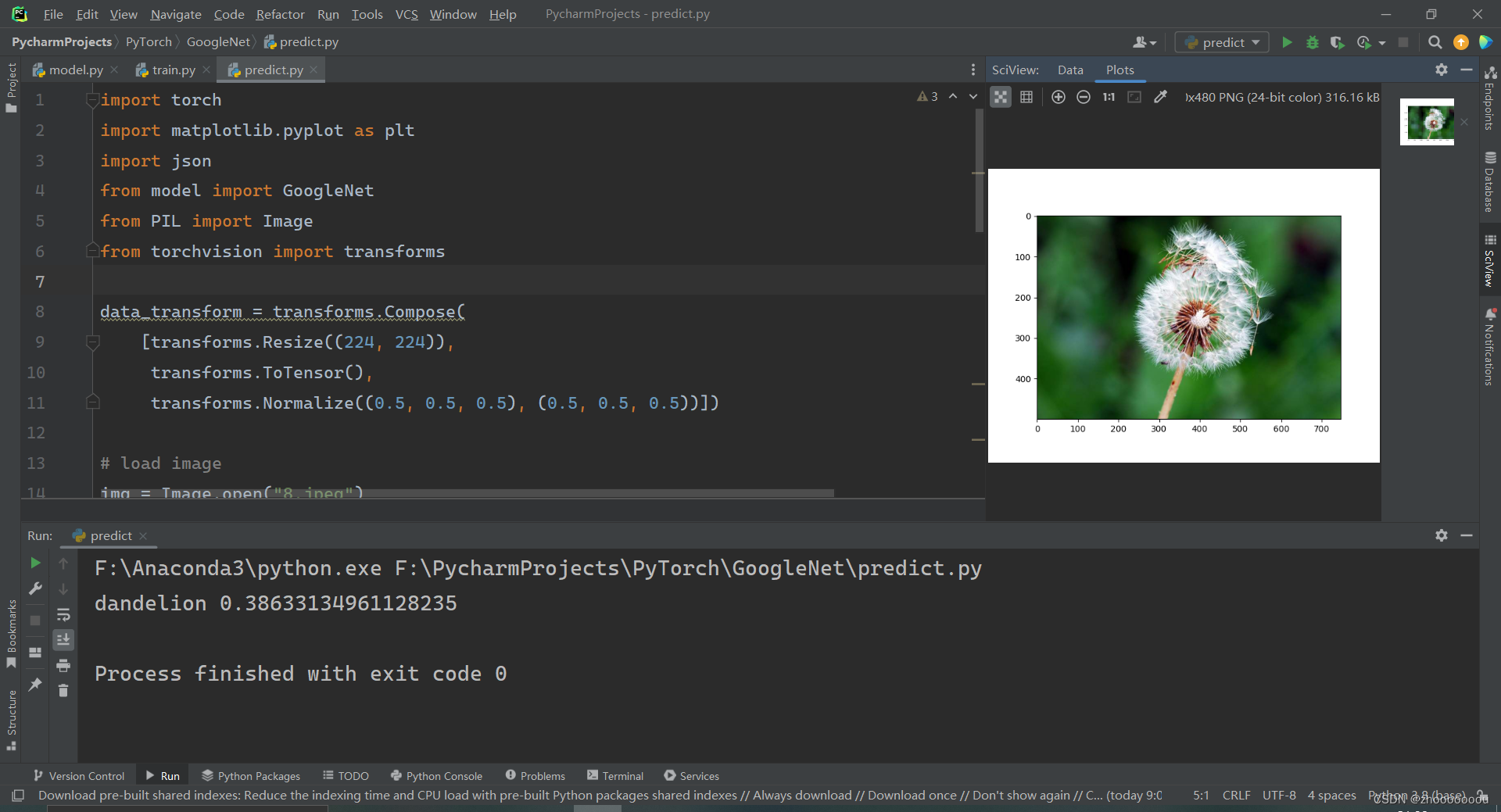
GoogleNet网络训练集和测试集搭建
测试集和训练集都是在之前搭建好的基础上进行修改的,重点记录与之前不同的代码。 还是使用的花分类的数据集进行训练和测试的。 一、训练集 1、搭建网络 设置参数:使用辅助分类器,采用权重初始化 net GoogleNet(num_classes5, aux_logi…...
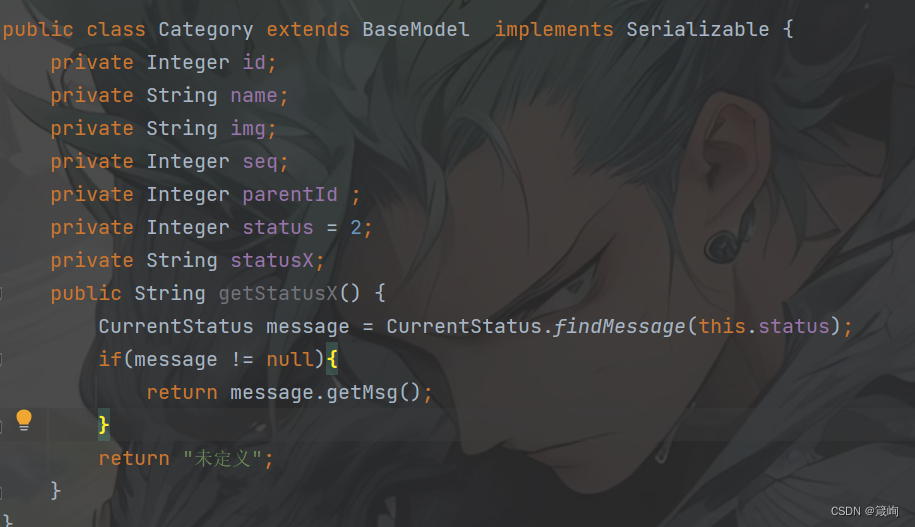
将数字状态码在后台转换为中文状态
这是我们的实体类 可以看出我们的状态status是2如过返回到前端我们根本不知道2代表的是什么,所以我们需要再这里将数字转换成能看懂的中文状态,首先我们创建一个枚举类 先将我们状态码所对应的中文状态枚举出来,然后创建一个静态方法&#…...

2017NOIP普及组真题 4. 跳房子
线上OJ: 一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid1417\ 核心思想 首先、本题中提到 “ 至少 要花多少金币改造机器人,能获得 至少 k分 ”。看到这样的话语,基本可以考虑要使用 二分答案。 那么,本题中…...

网络与 Internet因特网的基本概念
目录 网络Internet (互联网或互连网)Internet(因特网)待续、更新中 网络 指将分布在不同地理位置的、相同或不同类型的网络通过网络互连设备(中继器、网桥、路由器或网关等)相互连接,形成一个范…...

vue-router 中 router-link 与 a 标签的区别
文章目录 前言 a标签定义 router-link定义 总结 前言 vue-router 中 router-link 与 a 标签的区别 a标签定义 <a> 标签定义超链接,用于从一张页面链接到另一张页面。 从一张页面跳转到另一张页面,但从这里来说就违背了多视图的单页Web应用这个…...
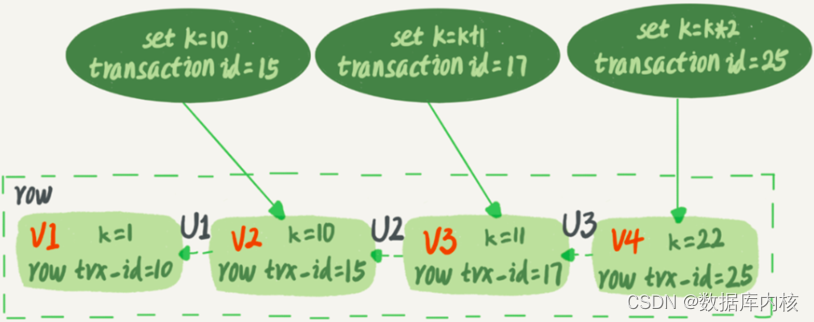
MySQL基础知识——MySQL事务
事务背景 什么是事务? 一组由一个或多个数据库操作组成的操作组,能够原子的执行,且事务间相互独立; 简单来说,事务就是要保证一组数据库操作,要么全部成功,要么全部失败。 注:MyS…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
