【C 数据结构】线性表
文章目录
- 【 1. 线性表 】
- 【 2. 顺序存储结构、链式存储结构 】
- 【 3. 前驱、后继 】
【 1. 线性表 】
- 线性表,全名为线性存储结构,线性表结构存储的数据往往是可以依次排列的(不考虑数值大小顺序)。
例如,存储类似 {1,3,5,7,9} 这样的数据时,各元素依次排列,每个元素的前面和后边有且仅有一个元素与之相邻(除首元素和尾元素),因此可以使用线性表存储。 - 使用线性表存储的数据,要求数据类型必须一致(如同向数组中存储数据那样,)。也就是说,线性表存储的数据,要么全部都是整形,要么全部都是字符串。一半是整形,另一半是字符串的一组数据无法使用线性表存储。
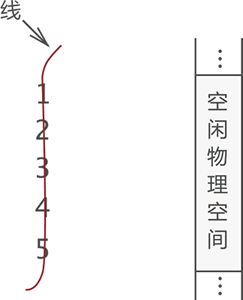
- 使用线性表存储数据的方式可以理解为 “把所有数据用一根线儿串起来,再存储到物理空间中”。
- 例如,数据为 1,2,3,4,5
- 用 “一根线儿” 把它们按照顺序“串”起来,左侧是“串”起来的数据,右侧是空闲的物理空间。
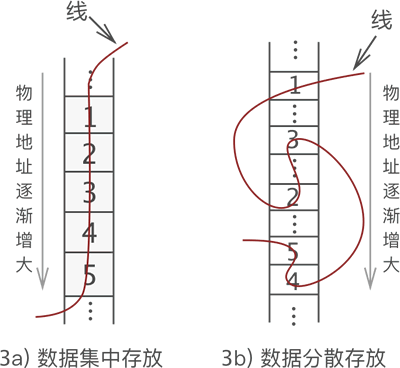
- 把这 “一串儿” 数据放置到物理空间,可以选择以下两种方式:左侧是顺序存储结构,右侧是链式存储结构。
【 2. 顺序存储结构、链式存储结构 】
- 上图中我们可以看出,线性表按存储结构可细分为顺序存储结构和链式存储结构。:
- 将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构,简称 顺序表;
- 将数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构,简称 链表;
【 3. 前驱、后继 】
- 数据结构中,一组数据中的每个个体被称为“数据元素”(简称 元素 )。
- 某一元素的左侧相邻元素称为 直接前驱 ,位于此元素左侧的所有元素都统称为“前驱元素”;
- 某一元素的右侧相邻元素称为 直接后继,位于此元素右侧的所有元素都统称为“后继元素”;
- 以数据 1,2,3,4,5 中的元素 3 来说,它的直接前驱是 2 ,此元素的前驱元素有 2 个,分别是 1 和 2;同理,此元素的直接后继是 4 ,后继元素也有 2 个,分别是 4 和 5。如图 4 所示:
相关文章:

【C 数据结构】线性表
文章目录 【 1. 线性表 】【 2. 顺序存储结构、链式存储结构 】【 3. 前驱、后继 】 【 1. 线性表 】 线性表,全名为线性存储结构,线性表结构存储的数据往往是可以依次排列的(不考虑数值大小顺序)。 例如,存储类似 {1…...

C++初级----list(STL)
1、 list介绍 1.1、 list介绍 1.list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 1. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向 其前一…...

web安全学习笔记(9)
记一下第十三课的内容。 准备工作:在根目录下创建template目录,将login.html放入其中,在该目录下新建一个reg.html。在根目录下创建一个function.php 一、函数声明与传参 PHP中的函数定义和其他语言基本上是相同的。我们编辑function.php …...

【Python-基础】字符串合集
字符串格式化 f # 例如: # f{train_path}/{f}: 将train_path字符串和f字符串结合 # f{root}.csv:将root字符串和.csv字符串结合判断字符串是否以…结尾 root.endswith(".csv") # True未待完续…...

Scala之List
列表 不可变列表(List) 在Scala中,通过List来定义不可变列表,需要注意的是,List本身是一个抽象类,所以并不能直接使用List来构建对象,需要使用它的伴生对象来构建 package com.fesco.listimport scala.::object ListD…...
Springboot+Vue项目-基于Java+MySQL的在线视频教育平台系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

Java IO流-字节流
简介 IO流的输入与输出,都在站在内存的角度来看的,因为毕竟是和内促你打交道的嘛! 分类 IO流是可以根据方向,或者最小单位进行划分的 上述两两结合一下,就得到四种大的分类 IO流的继承体系 字节输入流InputStream 创建…...
第十五届蓝桥杯复盘python大学A组——试题B 召唤数学精灵
按照正常思路解决,由于累乘消耗大量时间,因此这不是一个明智的解决方案。 这段代码执行速度非常慢的原因在于它试图计算非常大的数的阶乘(累乘),并且对于每一个i的值都执行这个计算。阶乘的增长是极其迅速的ÿ…...

网络通信——常见结构及强联网游戏和弱联网游戏区别
声明:本文为个人笔记,用于学习研究使用非商用,内容为个人研究及综合整理所得,若有违规,请联系,违规必改。 网络通信——常见结构及强联网游戏和弱联网游戏区别 文章目录 网络通信——常见结构及强联网游戏和…...

如何安装PyFluent
0.什么是PyFluent? 官方介绍如下: PyFluent 是 PyAnsys 生态系统的一部分, 允许您在所选的 Python 环境中结合使用 Fluent 与其他 PyAnsys 库和外部 Python 库一起使用。 PyFluent 实现了客户端-服务器体系结构。它使用谷歌遥控器 过程调用或 gRPC 接…...

Qt 2 QMapQHashQVector类实例
1. QMap // 1:QMap的使用// 创建一个QMap 实例 key 为 QString value 为 intQMap<QString,int> Grade;// 插入方式有两种插入方式// 1.map[key] valueGrade["语文"] 90;Grade["数学"] 120;// 2.map.insert(key,value);Grade.insert("英语&qu…...

使用Git将文件夹上传到Github以及使用Git LFS上传大文件
使用Git将文件夹上传到Github以及使用Git LFS上传大文件...
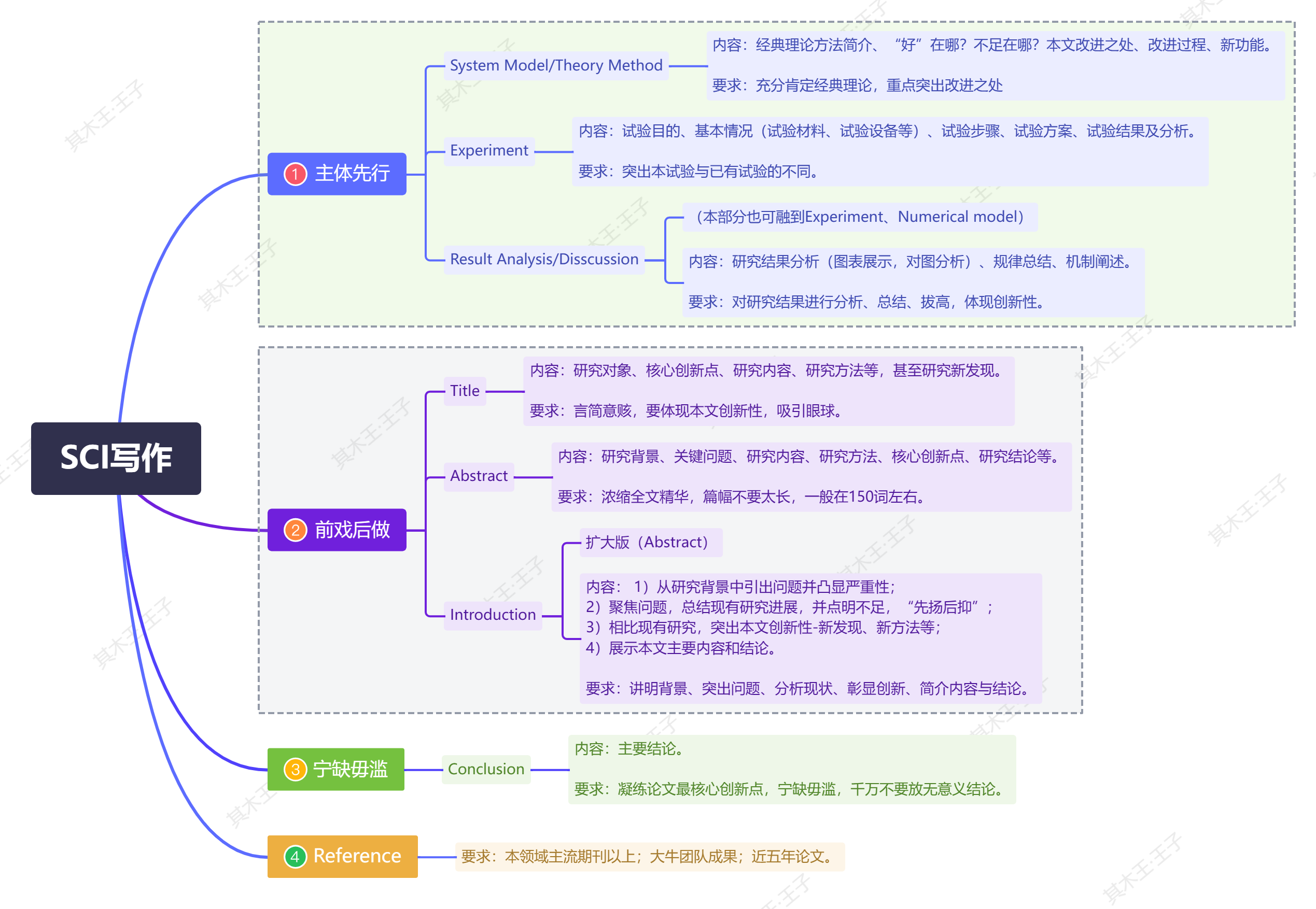
1.SCI各模块
1.学会“抄” 写论文,一定要学会“抄”!这样才能事半功倍,尤其是对于初次写作的新手,否则写作过程一定会让你痛不欲生,而且写出来的东西就是一坨shi,不仅折磨自己,也折磨导师。 写论文与建大楼…...
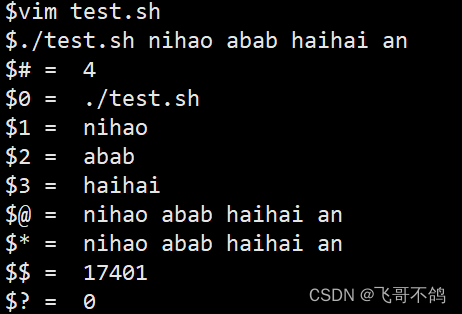
记录shell编程中$1,$@等符号的含义
笔者最近老是遇到shell中的$相关的题目,于是打算写篇文章记录一下。考虑到并没有特别多需要解释的内容,所以并不会进行介绍,上图上表上代码,让机器说话,machine always right test.sh #/bin/bash echo $# $# echo …...
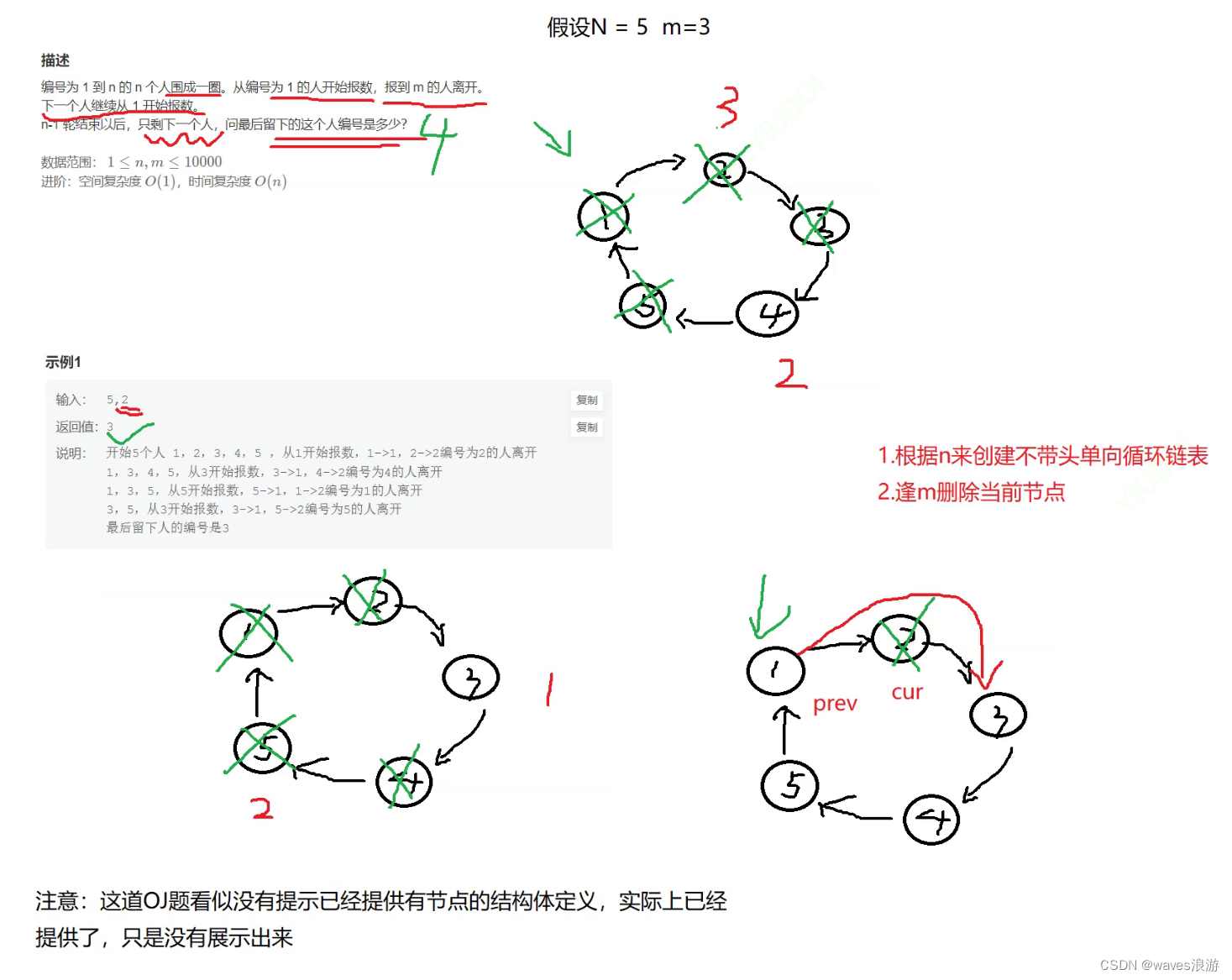
单链表的应用
文章目录 目录1. 单链表经典算法OJ题目1.1 [移除链表元素](https://leetcode.cn/problems/remove-linked-list-elements/description/)1.2 [链表的中间节点](https://leetcode.cn/problems/middle-of-the-linked-list/description/)1.3 [反转链表](https://leetcode.cn/problem…...

手机副业赚钱秘籍:让你的手机变成赚钱利器
当今社会,智能手机已然成为我们生活不可或缺的一部分。随着技术的飞速进步,手机不再仅仅是通讯工具,而是化身为生活伴侣与工作助手。在这个信息爆炸的时代,我们时常会被一种焦虑感所困扰:如何能让手机超越消磨时光的定…...
Flask之数据库连接池DBUtils库)
(二十七)Flask之数据库连接池DBUtils库
目录: 每篇前言:DBUtils库模式一(底层使用threading.local实现):模式二:Flask中使用方式一:直接将DBUtils初始化放到settings.py文件中方式二:从utils文件夹中导入脚本使用DBUtils代码demo:每篇前言: 🏆🏆作者介绍:【孤寒者】—CSDN全栈领域优质创作者、HDZ核心…...

FewShotPromptTemplate和SemanticSimilarityExampleSelector的学习
FewShotPromptTemplate 和 SemanticSimilarityExampleSelector 是在少样本学习(FewShot Learning)场景中常用的两种技术,它们在提高模型泛化能力和减少对大量标注数据的依赖方面扮演着重要角色。 下面我会解释它们之间的关系: F…...

【保姆级】2024年OnlyFans订阅指南
OnlyFans是一个独特的社交媒体平台,它为创作者和粉丝提供了一个互动交流的空间。通过这个平台,创作者可以分享他们的独家内容,而粉丝则可以通过订阅来支持和享受这些内容。如果你对OnlyFans感兴趣,并希望成为其中的一员࿰…...

深入理解JVM中的G1垃圾收集器原理、过程和参数配置
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 在Java虚拟机(JVM)中,垃圾收集(GC)是一个自动管理内存的过程ÿ…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...