2024蓝桥杯——宝石问题
先展示题目


声明
以下代码仅是我的个人看法,在自己考试过程中的优化版,本人考试就踩了很多坑,我会—一列举出来。代码可能很多,但是总体时间复杂度不高只有0(N²)
函数里面的动态数组我没有写开辟判断和free,这里我忽略掉了。
正文
先直接抛出最后的代码:

我也觉得太长了,大家可以当做知识点的掌握来看吧。
从数据中取出n个数的问题-->可以拓展到取出所有子集问题
先讲子集问题
这个问题我们可以用三个for循环来做,但是时间复杂度太高了。所以我们有以下的方法。
一个数取不取就有两种情况。我们可以用0或1来表示。那么我们就可以用二进制来表示我们的取或不取,用每位二进制的位置来对于每个元素。
例如:有1 2 两个数字。我们就可以用两位二进制来表示:00 01 10 11分别表示 不取任何数 取2 取1 都取。一共有2^2次方中情况
那么我们推广到n,就有2^n种。
我们来尝试写一下代码。
直接用二进制
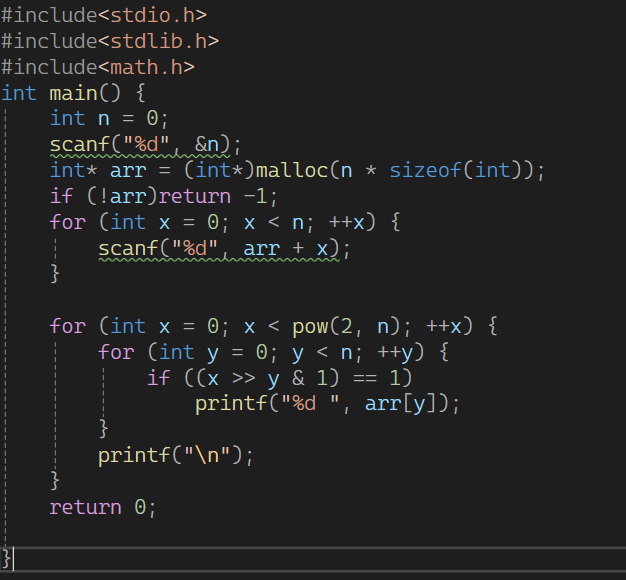

完全没问题。
用数组模拟二进制
这里有一个问题不知道大家看到没:2^n 容易溢出。因此我们可以用数组来模拟二进制的自增。
自增问题涉及到进一问题,所以我们需要运用到递归,递归的判断终止条件就是n+1位由0变成1。
所以我们需要开辟n+1长度的数组nums。
用类似递归来实现
用循环(最优解)

这里几个continue和return一定要有,不然逻辑就错了
这样的话我们就可以遍历任何长度的数组的子集了!
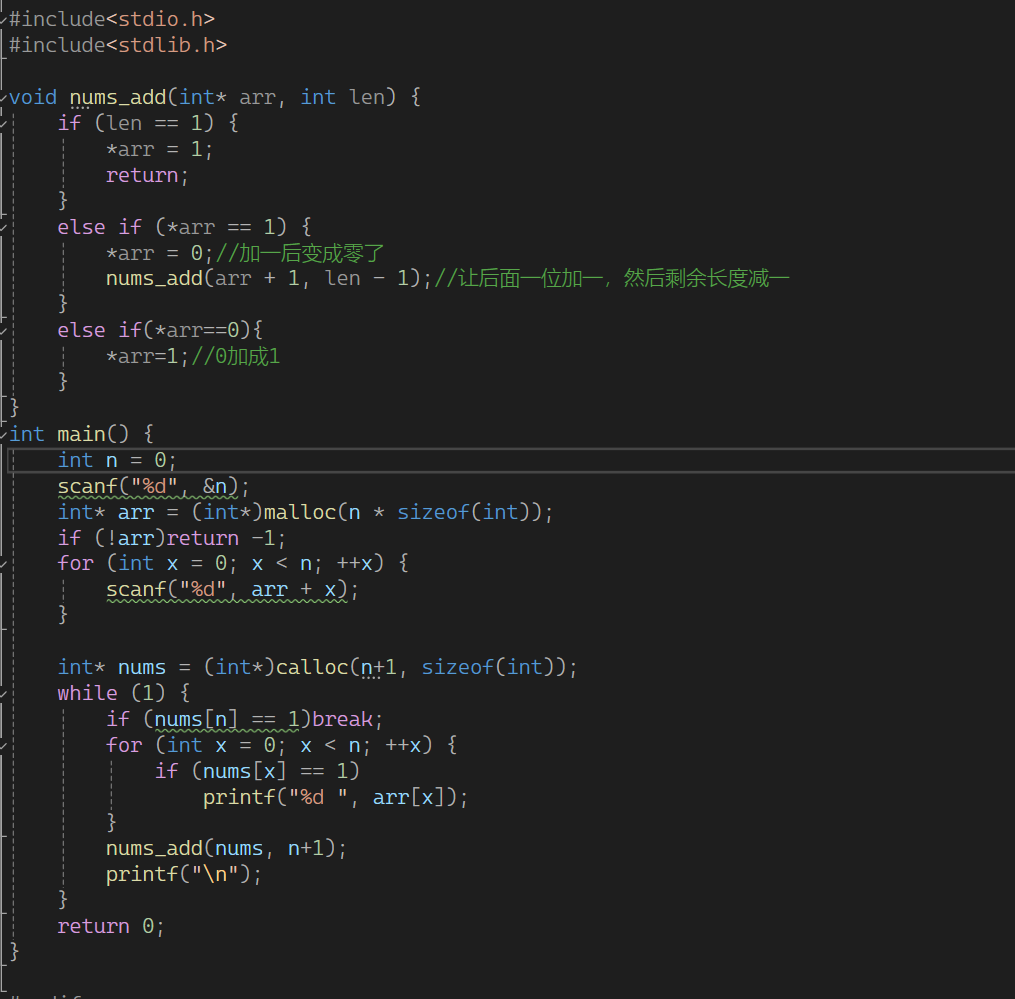
下面把代码给大家
#include<stdio.h>
#include<stdlib.h>
void nums_add(int* arr, int len) {
if (len == 1) {
*arr = 1;
return;
}
else if (*arr == 1) {
*arr = 0;//加一后变成零了
nums_add(arr + 1, len - 1);//让后面一位加一,然后剩余长度减一
}
else if(*arr==0){
*arr=1;//0加成1
}
}
void nums_add_(int* arr, int len) {
int k = len,i=0;
while (1) {
if (k == 1) {
arr[i] = 1;//如果长度为1了就退出
return;
}
if (arr[i] == 1) {
arr[i] = 0;
++i;
--k;
continue;//如果要进一我们还要循环一次,所以用continue
}
else if (arr[i] == 0) {
arr[i] = 1;
}
return;//到这里表示从0加到一,我们就不需要再循环了,直接结束循环
}
}
int main() {
int n = 0;
scanf("%d", &n);
int* arr = (int*)malloc(n * sizeof(int));
if (!arr)return -1;
for (int x = 0; x < n; ++x) {
scanf("%d", arr + x);
}
int* nums = (int*)calloc(n+1, sizeof(int));
int m[3];
while (1) {
nums_add_(nums, n + 1);
if (nums[n] == 1)break;
int k = 0;
for (int x = 0; x < n; ++x) {
if (nums[x] == 1)
{
if (k == 3)break;//已经有三个了还要存,直接跳过这个
m[k++] = arr[x];
}
}
if (k!=3)continue;//如果不等于三个,直接跳过到下一个循环
printf("%d %d %d",m[0],m[1],m[2]);
printf("\n");
}
return 0;
}
因为递归会开辟内存,所以后面的代码我们都用第二种非递归的
取出长度固定的所有子集
如果我们只要里面长度为3的子集怎么办呢?
自增变量来判断
我们可以在for循环里面先用一个长度为三的数组来存储我们的数据,再用一个变量来看是否满足。满足就打印。

在递归/非递归的时候就检测好
递归的时候我们完全就可以把1的数量统计好,所以可以做以下改变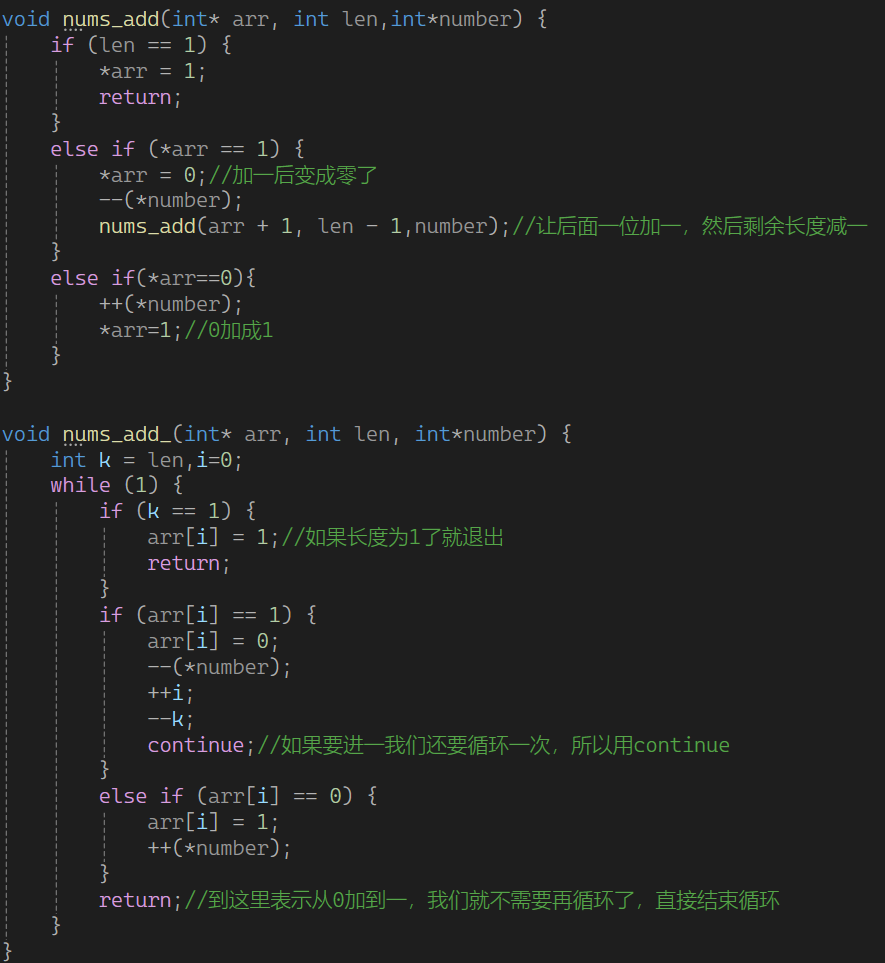

但是这样也没怎么变化嘛,那么我们既然可以知道1了,我们再储存一下有1的数组的位置可以吧?



这里我们发现是反着来的,我们把打印的顺序反过来就行了。因为这里的m数组相当于栈。
#include<stdio.h>
#include<stdlib.h>
void nums_add(int* begain_arr, int* arr, int* m, int* p, int len, int* number) {
if (len == 1) {
*arr = 1;
return;
}
else if (*arr == 1) {
*arr = 0;//加一后变成零了
--(*number);
if (*p>0) {
--p;
}
nums_add(arr,arr + 1,m,p, len - 1,number);//让后面一位加一,然后剩余长度减一
}
else if(*arr==0){
++(*number);
*arr=1;//0加成1
if (*p < 3) {
m[(*p)++] = (int)(arr - begain_arr);
}
}
}
void nums_add_(int* arr,int*m,int *p,int len, int*number) {
int k = len,i=0;
while (1) {
if (k == 1) {
arr[i] = 1;//如果长度为1了就退出
return;
}
if (arr[i] == 1) {
arr[i] = 0;
--(*number);
++i;
--k;
if (*p>0) {
--(*p);
}
continue;//如果要进一我们还要循环一次,所以用continue
}
else if (arr[i] == 0) {
arr[i] = 1;
++(*number);
if (*p < 3) {
m[(*p)++] =i;
}
}
return;//到这里表示从0加到一,我们就不需要再循环了,直接结束循环
}
}
int A_(int m, int n) {//非递归型
int k = 1, i = m, j = n;
while (1) {
if (i == 1)return k * j;
else {
k *= j;
--i;
--j;
}
}
}
int C_(int m, int n) {
return m == 0 ? 1 : A_(m, n) / A_(m, m);
}
int main() {
int n = 0;
scanf("%d", &n);
int* arr = (int*)malloc(n * sizeof(int));
if (!arr)return -1;
for (int x = 0; x < n; ++x) {
scanf("%d", arr + x);
}
int* nums = (int*)calloc(n+1, sizeof(int));
int m[3] , p = 0 , number1 = 0;//定义number1存储我们的1的数量
while (1) {
nums_add_(nums,m,&p, n + 1, &number1);
if (nums[n] == 1)break;
int k = 0;
if (number1 != 3)continue;
printf("%d %d %d",m[2],m[1],m[0]);
printf("\n");
}
return 0;
}
那么我们第一部分终于也是完成了,我嘞个豆真是多!!!!!!!!!!!!!!!!!!!!!!!!!
a,b的最小公倍数和最大公约数
我们题目要求的是最小公倍数,那么求这个我们可以枚举,但是时间复杂度复很高,所以我们就有特殊的算法。
我们首先要了解一个知识点就是
a*b=最大公约数(a,b)*最小公倍数(a,b)
我们求最小公倍数可能没有优秀的算法,但是我们最大公约数有优秀的算法。那么就可以通过这个式子进行转化。
辗转相除法求最大公约数
举个例子:求16 和 24的最大公约数
24%16 =8
16%8 = 0
所以答案是8
如果开始两个数字交换呢?
16%24=16
24%16=8
16%8=0
我们发现就是多了一部,没有太大差别。
那么我们开始实现
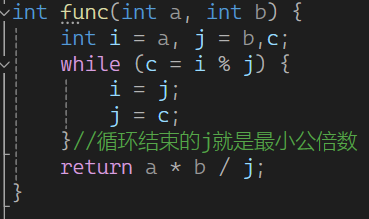
这里return的是最大公约数。
如果求三者的最大公约数或者最小公倍数,把其中两个数的先求出来,再看成整体和另一个求。
S
那么图中的表达式我们就可以算了
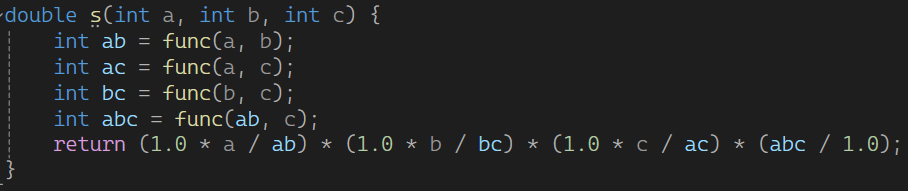
这里同样的,先除法再乘法,防止溢出了。
创建二维数组来存储三个都是1的数据。
我们就要用一个二维数组来储存我们的数据。那么每一个数组的长度是多少呢?
根据组合数我们要C(3,n)长度。排列组合在编程里面也很常见,我们也要知道他是怎么算出来的,排列组合我在下面讲到
排列组合函数
先是讲A(m,n)
如果m=n,那么就是算的阶乘。
我们可以通过A(m,n)=A(m-1,n-1)*n 来计算

C(m,n)
它有两个公式可以算,一个是C(m,n)=A(m,n)/A(n,n) 另一个是C(m,n)=n!/m!/(n-m)!
那么那个好呢?当然是第一个,第一个数字间相乘的次数少,不容易溢出。

储存后方便我们后面再取。
我们再用一个变量来存储S的最大值

那么我们的宝石问题就完成了。
真的完成了吗?
no no no
存储根本不需要二维数组,我写到这才发现,我们只要用一个长度为3个数组来储存最大的数据就行了
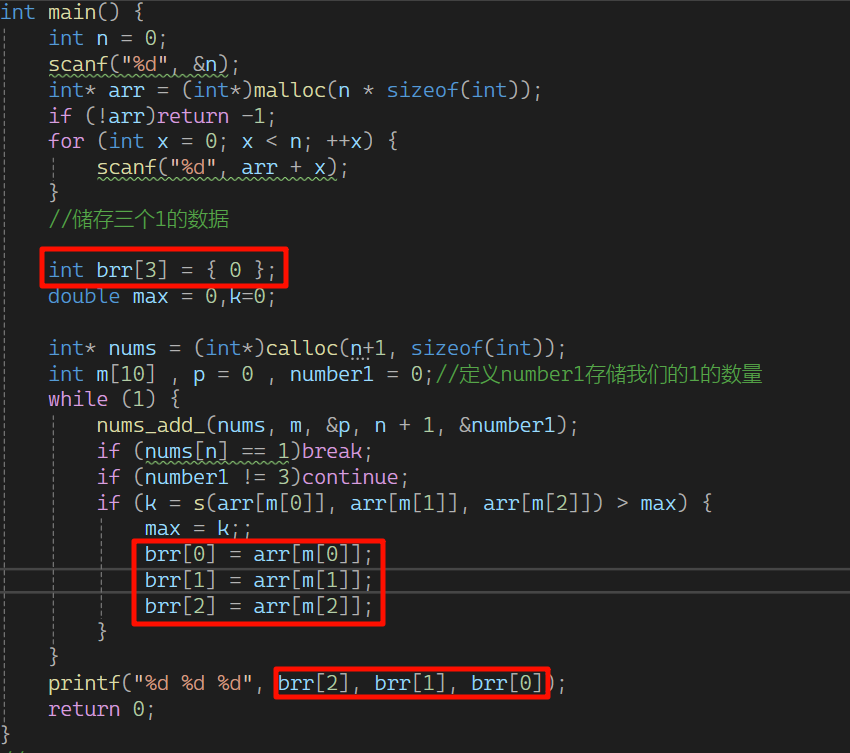
那么我们的排列组合函数就不需要了。
另外补充
我们m数组的长度定义的太短了,会产生越界访问。所以可以将m数组的长度定义长一点。可以和arr的数组一样长.
提前排序来解决字典序要求
我们的代码已经可以计算了,但是还有最后一个坑。例如我们逆向输入
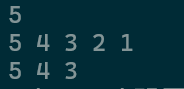
因为S(5,4,3)和S(1,2,3)的值是一样的,所以我们不会存后面字典序小的数据。我们最要先将数据进行排序。
这里我们光速搓一个快排出来

在计算之前排好序就行了。
最终的代码
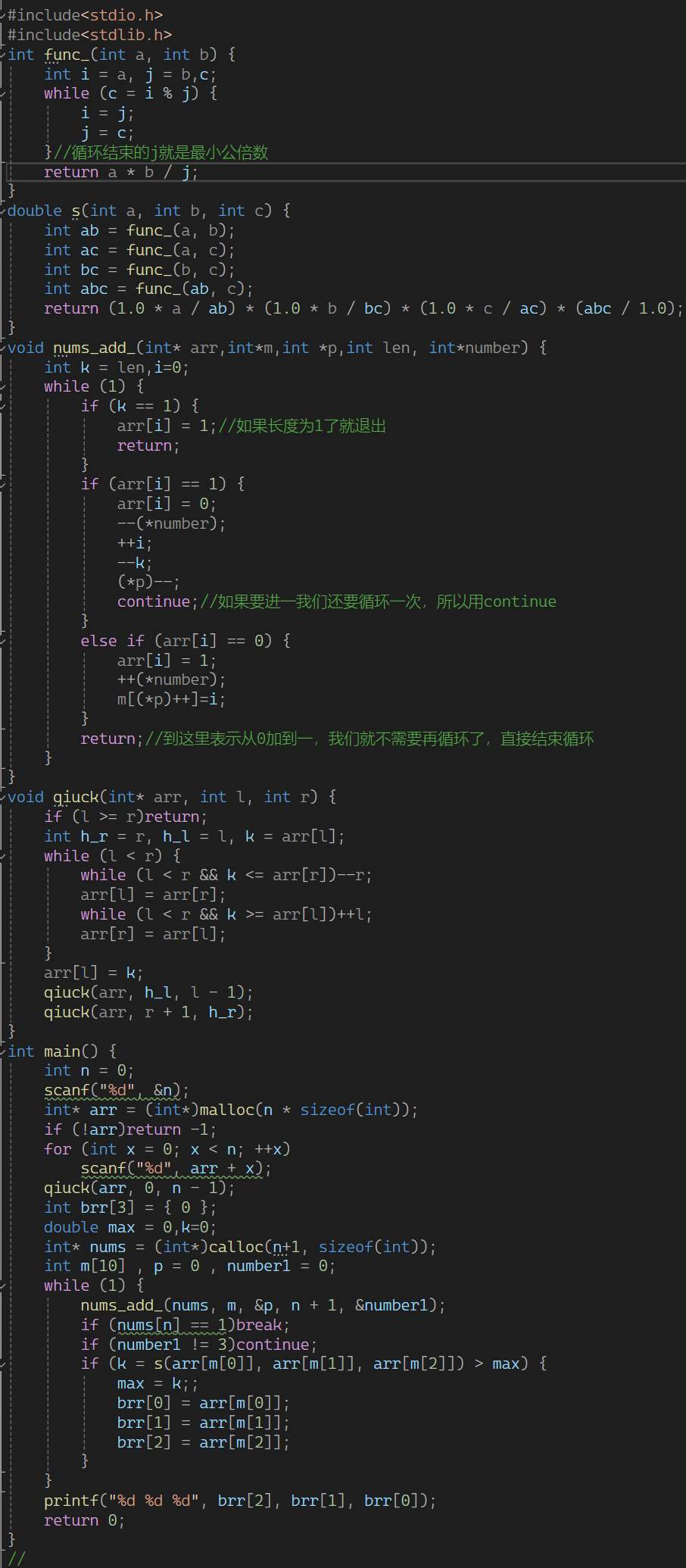
相关文章:

2024蓝桥杯——宝石问题
先展示题目 声明 以下代码仅是我的个人看法,在自己考试过程中的优化版,本人考试就踩了很多坑,我会—一列举出来。代码可能很多,但是总体时间复杂度不高只有0(N) 函数里面的动态数组我没有写开辟判断和free,这里我忽略…...

three.js加载模型报错,Error: THREE.GLTFLoader: No DRACOLoader instance provided.
three.js加载模型报错,Error: THREE.GLTFLoader: No DRACOLoader instance provided. 原因:该模型是压缩过的,需要 DRACOLoader 我们先找到该文件夹 node_modules three examples jsm libs draco 将draco拷贝到public下 import { GLTFLoad…...

Spring VS Spring Boot
目录 定义 Spring Spring Boot 区别 优劣对比 Spring Spring的优势 Spring的劣势 Spring Boot Spring Boot的优势 Spring Boot的劣势 适用场景 Spring的适用场景 Spring Boot的适用场景 初学者如何选择学习 定义 Spring Spring是一个轻量级的、开源的Java开发…...
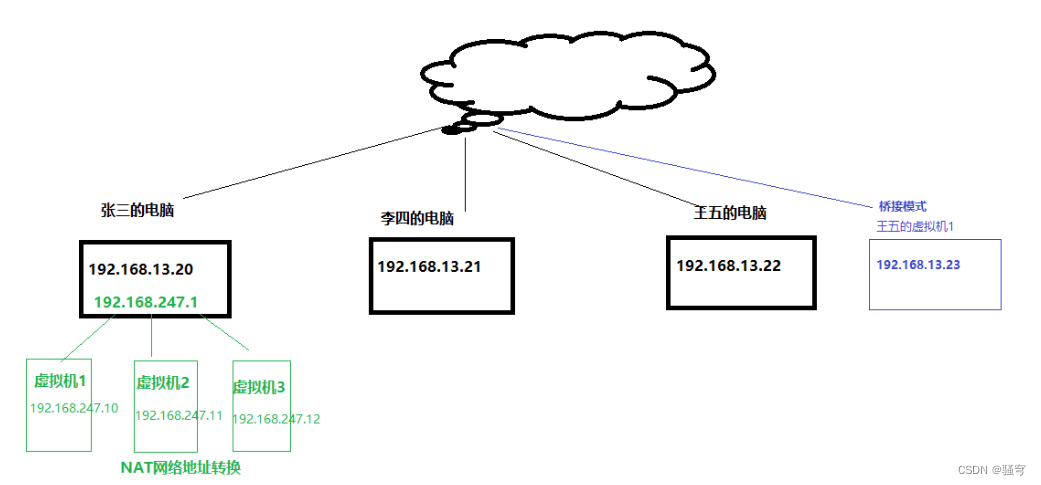
Linux入门(Linux介绍,安装,常用命令,防火墙的设置,注意事项)
目录 一、Linux介绍 1. Linux简介 1 什么是Linux 2 Linux的应用 3 为什么要学习Linux 2. Linux分类 1 按照市场需求分 2 按照原生程度分 3.小结 二、Linux安装 1. vmware介绍 2. 安装VMWare 3. 安装CentOS 4. 登录查看ip 5. 远程连接工具 1 使用FinalShell连接L…...
vue2创建项目的两种方式,配置路由vue-router,引入element-ui
提示:vue2依赖node版本8.0以上 文章目录 前言一、创建项目基于vue-cli二、创建项目基于vue/cli三、对吧两种创建方式四、安装Element ui并引入五、配置路由跳转四、效果五、参考文档总结 前言 使用vue/cli脚手架vue create创建 使用vue-cli脚手架vue init webpack创…...
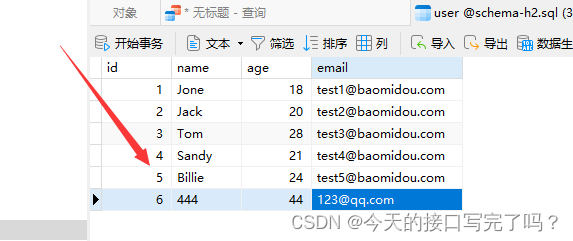
MySql 表中的id突然变很大,如何给id重新排序
目录 一、场景 二、解决方法 一、场景 我们在开发过程中,难免遇到id突然增大的情况。 由于id突然增大很多,我们重新增加数据时候id会默认加1 那么如何让id 重新从1按顺序排序呢 二、解决方法 点击编辑表,然后新建一个字段id2,将…...

leetcode练习——哈希表
目录 3. 无重复字符的最长子串 题目描述 解题思路 代码实现 349. 两个数组的交集 题目描述 解题思路 代码实现 454. 四数相加 II 题目描述 解题思路 代码实现 242. 有效的字母异位词 题目描述 解题思路 代码实现 438. 找到字符串中所有字母异位词 题目…...
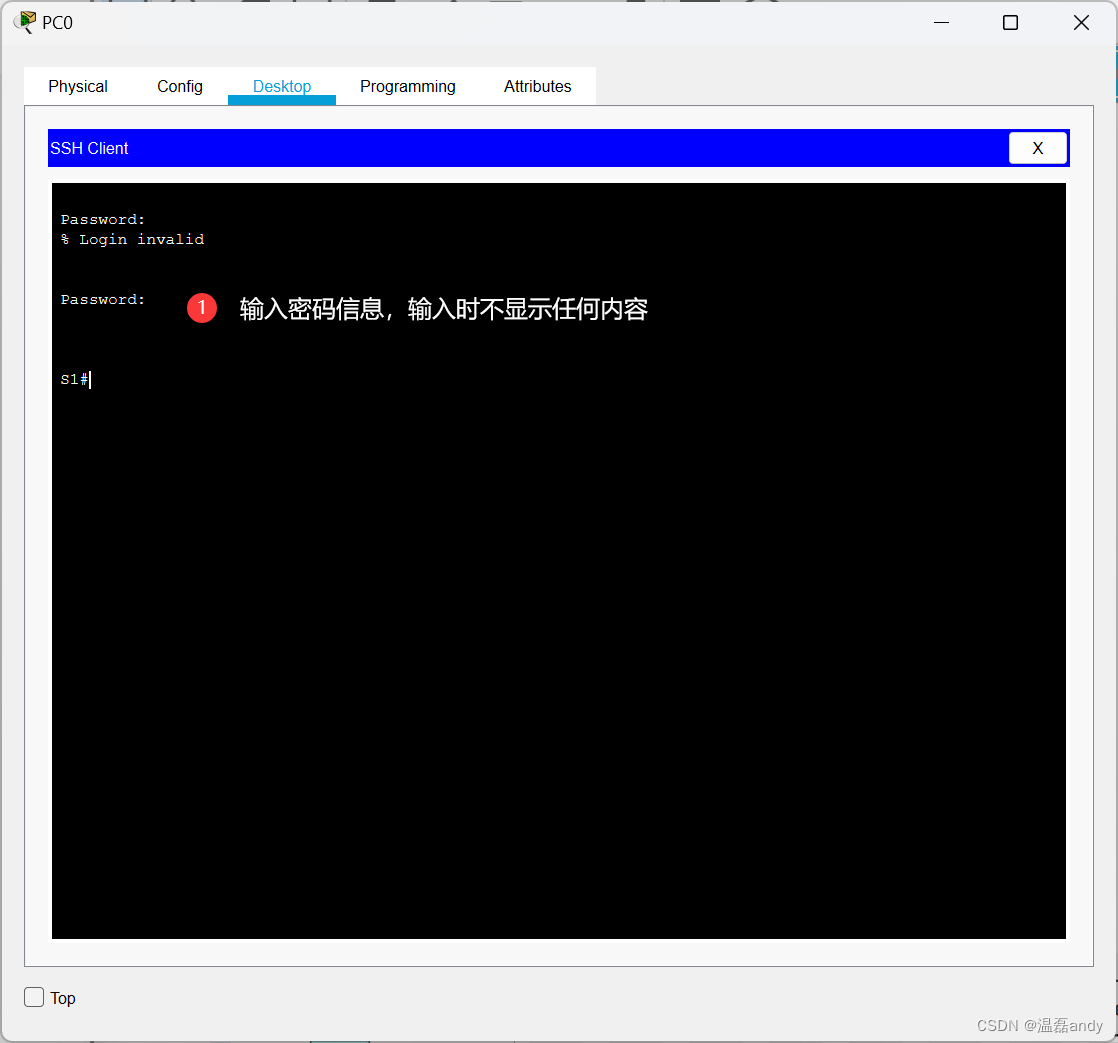
配置交换机 SSH 管理和端口安全
实验1:配置交换机基本安全和 SSH管理 1、实验目的 通过本实验可以掌握: 交换机基本安全配置。SSH 的工作原理和 SSH服务端和客户端的配置。 2、实验拓扑 交换机基本安全和 SSH管理实验拓扑如图所示。 3、实验步骤 (1)配置交换机S1 Swit…...

基于SpringBoot+Vue的装饰工程管理系统(源码+文档+包运行)
一.系统概述 如今社会上各行各业,都喜欢用自己行业的专属软件工作,互联网发展到这个时候,人们已经发现离不开了互联网。新技术的产生,往往能解决一些老技术的弊端问题。因为传统装饰工程项目信息管理难度大,容错率低&a…...

vue3中axios添加请求和响应的拦截器
本章主要是以记录为主。 在src创建一个utils文件夹,并在utils中创建一个request.js文件。 // 引入axios import axios from "axios"; // import qs from "qs"; // 创建axios实例 const instance axios.create(); // 请求拦截器 instance.int…...
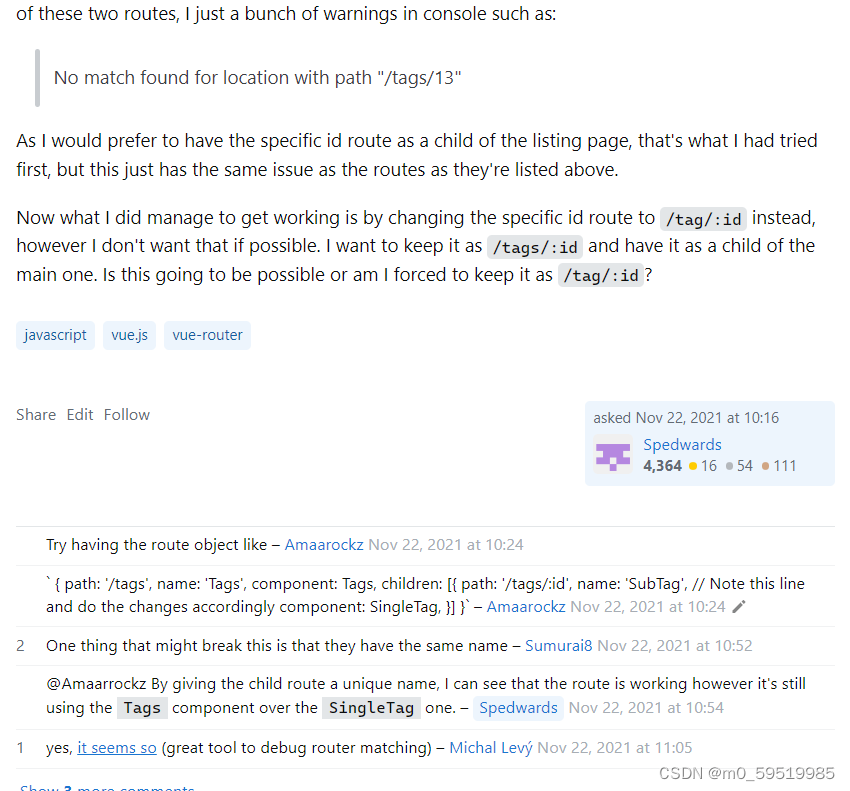
<router-link>出现Error: No match for {“name“:“home“,“params“:{}}
在将<a></a>标签换到<router-link></router-link>的时候出现No match for {"name":"home","params":{}}这样的错误,其中格式并无错误, <router-link class"navbar-brand active" …...
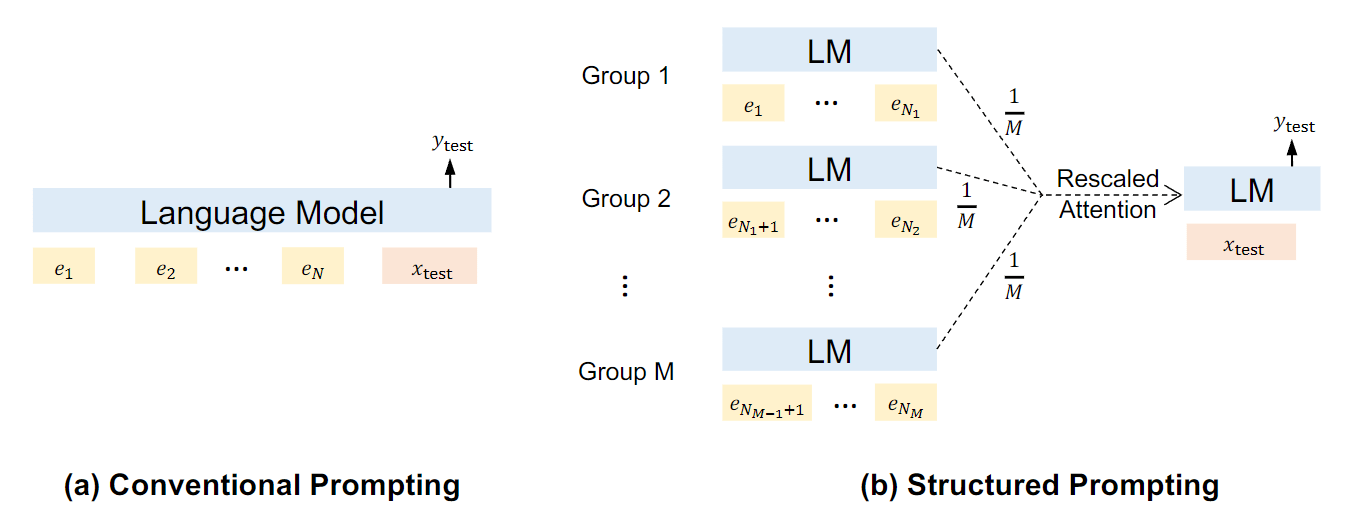
prompt 工程整理(未完、持续更新)
工作期间会将阅读的论文、一些个人的理解整理到个人的文档中,久而久之就积累了不少“个人”能够看懂的脉络和提纲,于是近几日准备将这部分略显杂乱的内容重新进行梳理。论文部分以我个人的理解对其做了一些分类,并附上一些简短的理解…...

兼容性测试用例
备注:本文为博主原创文章,未经博主允许禁止转载。如有问题,欢迎指正。 个人笔记(整理不易,有帮助,收藏+点赞+评论,爱你们!!!你的支持是我写作的动力) 笔记目录:学习笔记目录_pytest和unittest、airtest_weixin_42717928的博客-CSDN博客 个人随笔:工作总结随笔_8、…...
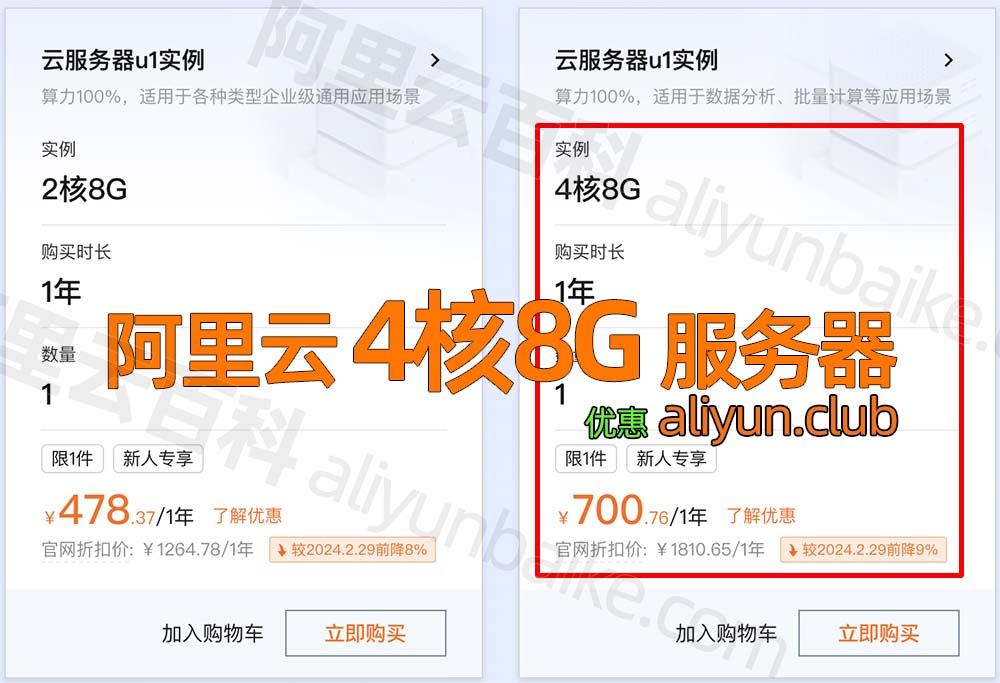
阿里云4核8G云服务器价格多少钱?700元1年
阿里云4核8G云服务器价格多少钱?700元1年。阿里云4核8G服务器租用优惠价格700元1年,配置为ECS通用算力型u1实例(ecs.u1-c1m2.xlarge)4核8G配置、1M到3M带宽可选、ESSD Entry系统盘20G到40G可选,CPU采用Intel(R) Xeon(R…...

ts 中的keyof 和typeof
作用: keyof:用于获取对象类型的所有键的联合类型。typeof:用于获取变量或表达式的类型。 返回类型: keyof:返回的是一个对象类型的所有键组成的联合类型。typeof:返回的是一个值的类型。 使用场景…...

每日一题:买卖股票的最佳时机II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。 返回 你能获得的 最大 利润 。 示例 1&a…...
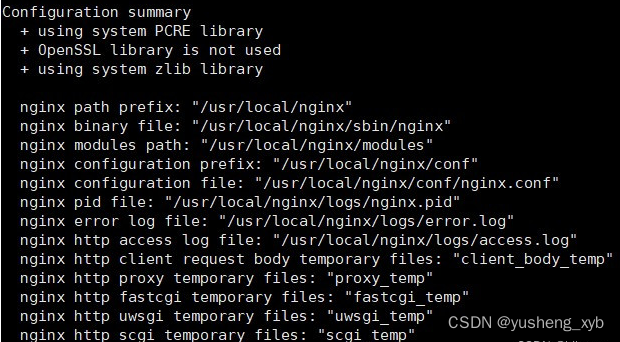
nginx安装在linux上
nginx主要用于反向代理和负载均衡,现在简单的说说如何在linux操作系统上安装nginx 第一步:安装依赖 yum install -y gcc-c pcre pcre-devel zlib zlib-devel openssl openssl-devel 第二步: 下载nginx,访问官网,ngin…...
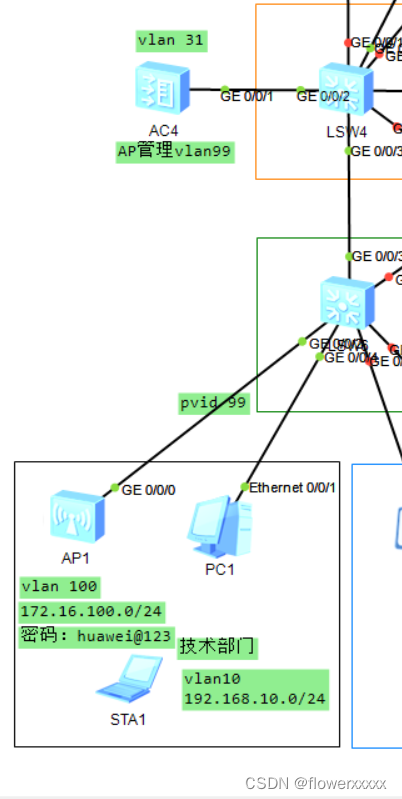
ENSP-旁挂式AC
提醒:如果AC不能成功上线AP,一般问题不会出在AC上,优先关注AC-AP线路上的二层或三层组网的三层交换机 拓扑图 管理VLAN:99 | 业务VLAN:100 注意点: 1.连接AP的接口需要打上pvid为管理vlan的标签 2.AC和…...

如何获取手机root权限?
获取手机的 root 权限通常是指在 Android 设备上获取超级用户权限,这样用户就可以访问和修改系统文件、安装定制的 ROM、管理应用权限等。然而,需要注意的是,获取 root 权限可能会导致手机失去保修、安全性降低以及使系统变得不稳定。在获取 …...
海南赛区复赛真题)
2023年全国青少年信息素养大赛(Python)海南赛区复赛真题
2023年全国青少年信息素养大赛(Python)海南赛区复赛真题第1题,整数加8 题目描述: 输入一个整数,输出这个整数加8 的结果。 输入描述: 输入一行一个正整数。 输出描述: 输出求和的结果。 样例1: 输入: 5 输出: 13 x= int(input()) print(x+8) 第2题,哼哈二将 题目描…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...