B树(B-tree)
B树(B-tree)
B树(B-tree)是一种自平衡的多路查找树,主要用于磁盘或其他直接存取的辅助存储设备
B树能够保持数据有序,并允许在对数时间内完成查找、插入及删除等操作
这种数据结构常被应用在数据库和文件系统的实现上
B树的特点包括:
B树为了表示节点个数 通常称为 M阶树
1.M阶树每个结点至多有M棵子树(M>=2)
2.每个非根节点至少有 M/2(向上取整)个孩子,至多有M个孩子。
3.每个叶子节点至少有 M/2-1 个关键字,至多有M-1个关键字,并以升序排列
4.所有叶子节点都在同一层
5.非叶子节点的关键字个数等于其孩子数减一
6.所有叶子节点不含有任何信息
按照子节点数 y:非根节点至少有 M/2(向上取整)个孩子,至多有M个孩子
M = 3, 2 <= y <= 3, 因此称为:2-3树
M = 4, 2 <= y <= 4, 因此称为:2-3-4树
M = 5, 3 <= y <= 5, 因此称为:3-5树
M = 7, 4 <= y <= 7, 因此称为:4-7树
B树的高度对于含有n个关键字的m阶B树,其高度为O(log n)
这种数据结构通过减少定位记录时所经历的中间过程,从而加快存取速度
与自平衡的二叉查找树不同,B树为系统大块数据的读写操作做了优化
下面先看 B树节点的定义
class BTNode<T> where T : IComparable<T>
{private BTNode<T> parentNode; // 父节点private List<T> keyList; // 关键字向量private List<BTNode<T>> childList; // 子节点向量(其长度总比key多一)
}
B树每个节点存储的关键字是从小到大有序的:keyList 是从小到大排序的
B树 关键字个数 比 子节点 个数少 1 个,为什么?
因为 关键字 和 子节点 可以理解为这么样一个排序,假设一个 5 阶树的一个节点
childList[0],keyList[0],childList[1],keyList[1],childList[2]
可以看到 子节点 和 关键字 是交替出现的,并且 子节点 比 关键字 个数多 1 个
并且还有一个隐藏的信息
1.子树中所有关键字的值,比其右侧的关键字都小
2.子树中所有关键字的值,比其左侧的关键字都大
什么意思呢?
1.(childList[0] 子树下所有节点的关键字) 小于 keyList[0]
2. keyList[0] 小于 (childList[1] 子树下所有节点的关键字)
看下图 一个 5阶树

Node0 包含 三个关键字(25,39,66),四个子节点(Node1,Node2,Node3,Node4)
25 对应 keyList[0]
39 对应 keyList[1]
66 对应 keyList[2]
Node0 包含 两个关键字 (5, 13) < 25
Node1 包含 两个关键字 25 < (28, 30) < 39
Node2 包含 两个关键字 39 < (40, 55) < 66
Node3 包含 两个关键字 66 < (67, 68, 90)
B树在操作 插入、删除的过程中往往会导致
上溢:节点个数大于 B树限制
下移:节点个数小于 B树限制
需要通过一系列操作将树恢复平衡
B树操作逻辑
查询: number
1.根节点作为当前节点
2. number 顺次与当前节点的关键字作比较
如果 number < keyList[index],则 number 一定在 childList[index],令当前节点= childList[index] 循环执行 2
如果 number = keyList[index],则 在关键字中找到 了number,查询完成,返回节点
如果 number > keyList[index], index++,如果 index >= childList.Count,查找失败,返回,否则继续循环执行 2 ,比较下一个 关键字 keyList[index]
我在查询操作逻辑中隐含保留了一个 hot 节点,这个 hot 节点是最接近 number 的节点,如果查询成功,则 hot 不再起作用,如果查询失败,在 插入操作中 是有用处的
插入: number
1.先执行查询操作,如果查询到节点,则说明已经存在,不再添加,返回
2.查询逻辑中 保存的 hot 节点是最接近 numbe 的节点,我们将 number 插入到hot节点
3.令 number 与 keyList 中的数据比较
如果 keyList[i] < number, 将 number 插入到 keyList第 i + 1 位置,然后 childList 第 i + 2 位置插入一个空节点
如果 keyList 中的关键字 > number,将 number 插入到 keyList 第 0 个位置,然后 childList 第 1 个位置插入一个空节点
4. 如果 hot 节点发生上溢,做分裂处理
C#代码实现如下
B树节点定义
/// <summary>/// B-树节点定义/// </summary>/// <typeparam name="T"></typeparam>class BTNode<T> where T : IComparable<T>{private BTNode<T> parentNode; // 父节点private List<T> keyList; // 关键字向量private List<BTNode<T>> childList; // 子节点向量(其长度总比key多一)public BTNode(){keyList = new List<T>();childList = new List<BTNode<T>>();childList.Insert(0, null);}public BTNode(T t, BTNode<T> lc, BTNode<T> rc){parentNode = null;keyList.Insert(0, t);// 左右孩子childList.Insert(0, lc);childList.Insert(1, rc);if (null != lc){lc.parentNode = this;}if (null != rc){rc.parentNode = this;}}public BTNode<T> ParentNode{get { return parentNode; }set { parentNode = value; }}private List<T> KeyList{get { return keyList; }set { keyList = value; }}public int KeyCount{get { return KeyList.Count; }}public void InsertKey(int index, T key){KeyList.Insert(index, key);}public T GetKey(int index){return KeyList[index];}public void RemoveKeyAt(int index){KeyList.RemoveAt(index);}public void SetKey(int index, T key){KeyList[index] = key;}private List<BTNode<T>> ChildList{get { return childList; }set { childList = value; }}public void InsertChild(int index, BTNode<T> node){ChildList.Insert(index, node);if (null != node){node.parentNode = this;}}public BTNode<T> GetChild(int index){return ChildList[index];}public void AddChild(BTNode<T> node){InsertChild(ChildList.Count, node);}public BTNode<T> RemoveChildAt(int index){BTNode<T> node = ChildList[index];ChildList.RemoveAt(index);return node;}public void SetChild(int index, BTNode<T> node){ChildList[index] = node;}public int ChildCount{get { return ChildList.Count; }}}
B树实现
/// <summary>/// B-树/// </summary>/// <typeparam name="T"></typeparam>class BTree<T> where T : IComparable<T>{private int _order; // 介次protected BTNode<T> _root; // 跟节点protected BTNode<T> _hot; // search() 最后访问的非空节点位置public BTree(int order){_order = order;}public BTNode<T> Root{get { return _root; }set { _root = value; }}/// <summary>/// 查找/// </summary>public BTNode<T> Search(T t){BTNode<T> v = Root; // 从根节点触发_hot = null;while (null != v){int index = -1;for (int i = 0; i < v.KeyCount; ++i){int compare = v.GetKey(i).CompareTo(t);if (compare <= 0){index = i;if (compare == 0){break;}}}// 若成功,则返回if (index >= 0 && v.GetKey(index).CompareTo(t) == 0){return v;}_hot = v;// 沿引用转至对应的下层子树,并载入其根v = v.ChildCount > (index + 1) ? v.GetChild(index + 1) : null;}// 若因 null == v 而退出,则意味着抵达外部节点return null; // 失败}/// <summary>/// 插入/// </summary>public bool Insert(T t){BTNode<T> node = Search(t);if (null != node){return false;}int index = -1;for (int i = 0; i < _hot.KeyCount; ++i){int compare = _hot.GetKey(i).CompareTo(t);if (compare <= 0){index = i;if (compare == 0){break;}}}_hot.InsertKey(index + 1, t); // 将新关键码插至对应的位置_hot.InsertChild(index + 2, null); // 创建一个空子树指针SolveOverflow(_hot); // 如发生上溢,需做分裂return true;}/// <summary>/// 删除/// </summary>public bool Remove(T t){BTNode<T> node = Search(t);if (null == node){return false;}int index = -1;for (int i = 0; i < node.KeyCount; ++i){if(node.GetKey(i).CompareTo(t) == 0){index = i;break;}}// node 不是叶子节点if (null != node.GetChild(0)){BTNode<T> u = node.GetChild(index + 1); // 在右子树中一直向左,即可while (null != u.GetChild(0)){u = u.GetChild(0); // 找到 t 的后继(必需于某叶节点)}// 至此,node 必然位于最底层,且其中第 r 个关键码就是待删除者node.SetKey(index, u.GetKey(0));node = u; // 并与之交换位置index = 0;}node.RemoveKeyAt(index);node.RemoveChildAt(index + 1);SolveUnderflow(node); // 如有必要,需做旋转或合并return false;}/// <summary>/// 上溢:因插入而上溢后的分裂处理/// </summary>private void SolveOverflow(BTNode<T> v){if (_order >= v.ChildCount){return; //递归基:当前节点并未上溢}int s = _order / 2; //轴点(此时应有_order = key.Count = child.Count - 1)BTNode<T> u = new BTNode<T>(); //注意:新节点已有一个空孩子for (int j = 0; j < _order - s - 1; j++){ //v右侧_order-s-1个孩子及关键码分裂为右侧节点uBTNode<T> node = v.GetChild(s + 1);v.RemoveChildAt(s + 1);u.InsertChild(j, node); //逐个移动效率低T key = v.GetKey(s + 1);v.RemoveKeyAt(s + 1);u.InsertKey(j, key); //此策略可改进}BTNode<T> node2 = v.GetChild(s + 1);v.RemoveChildAt(s + 1);u.SetChild(_order - s - 1, node2); //移动v最靠右的孩子if (null != u.GetChild(0)) //若u的孩子们非空,则{for (int j = 0; j < _order - s; j++) //令它们的父节点统一{u.GetChild(j).ParentNode = u; //指向u}}BTNode<T> p = v.ParentNode; //v当前的父节点pif (null == p){_root = p = new BTNode<T>();p.SetChild(0, v);v.ParentNode = p;} //若p空则创建之int index = -1;for (int i = 0; i < p.KeyCount; ++i){int compare = p.GetKey(i).CompareTo(v.GetKey(0));if (compare <= 0){index = i;if (compare == 0){break;}}}int r = 1 + index; //p中指向u的指针的秩T key2 = v.GetKey(s);v.RemoveKeyAt(s);p.InsertKey(r, key2); //轴点关键码上升p.InsertChild(r + 1, u); u.ParentNode = p; //新节点u与父节点p互联SolveOverflow(p); //上升一层,如有必要则继续分裂——至多递归O(logn)层}/// <summary>/// 下溢:因删除而下溢后的合并处理/// </summary>/// <param name="node"></param>private void SolveUnderflow(BTNode<T> v){if ((_order + 1) / 2 <= v.ChildCount) return; //递归基:当前节点并未下溢BTNode<T> p = v.ParentNode;if (null == p){ //递归基:已到根节点,没有孩子的下限if (v.KeyCount <= 0 && null != v.GetChild(0)){//但倘若作为树根的v已不含关键码,却有(唯一的)非空孩子,则/*DSA*/_root = v.GetChild(0);_root.ParentNode = null; //这个节点可被跳过v.SetChild(0, null); //release(v); //并因不再有用而被销毁} //整树高度降低一层return;}int r = 0;while (p.GetChild(r) != v){r++;}//确定v是p的第r个孩子——此时v可能不含关键码,故不能通过关键码查找//另外,在实现了孩子指针的判等器之后,也可直接调用Vector::find()定位/*DSA*/// 情况1:向左兄弟借关键码if (0 < r){ //若v不是p的第一个孩子,则BTNode<T> ls = p.GetChild(r - 1); //左兄弟必存在if ((_order + 1) / 2 < ls.ChildCount){ //若该兄弟足够“胖”,则/*DSA*/v.InsertKey(0, p.GetKey(r - 1)); //p借出一个关键码给v(作为最小关键码)T key = ls.GetKey(ls.KeyCount - 1);ls.RemoveKeyAt(ls.KeyCount - 1);p.SetKey(r - 1, key); //ls的最大关键码转入pBTNode<T> node = ls.GetChild(ls.ChildCount - 1);ls.RemoveChildAt(ls.ChildCount - 1);//同时ls的最右侧孩子过继给v//作为v的最左侧孩子v.InsertChild(0, node);return; //至此,通过右旋已完成当前层(以及所有层)的下溢处理}} //至此,左兄弟要么为空,要么太“瘦”// 情况2:向右兄弟借关键码if (p.ChildCount - 1 > r){ //若v不是p的最后一个孩子,则BTNode<T> rs = p.GetChild(r + 1); //右兄弟必存在if ((_order + 1) / 2 < rs.ChildCount){ //若该兄弟足够“胖”,则/*DSA*/v.InsertKey(v.KeyCount, p.GetKey(r)); //p借出一个关键码给v(作为最大关键码)T key = rs.GetKey(0);rs.RemoveKeyAt(0);p.SetKey(r, key); //rs的最小关键码转入pBTNode<T> node = rs.GetChild(0);rs.RemoveChildAt(0);v.InsertChild(v.ChildCount, node);//同时rs的最左侧孩子过继给vif (null != v.GetChild(v.ChildCount - 1)) //作为v的最右侧孩子{v.GetChild(v.ChildCount - 1).ParentNode = v;}return; //至此,通过左旋已完成当前层(以及所有层)的下溢处理}} //至此,右兄弟要么为空,要么太“瘦”// 情况3:左、右兄弟要么为空(但不可能同时),要么都太“瘦”——合并if (0 < r){ //与左兄弟合并/*DSA*/BTNode<T> ls = p.GetChild(r - 1); //左兄弟必存在T key = p.GetKey(r - 1);p.RemoveKeyAt(r - 1);ls.InsertKey(ls.KeyCount, key);p.RemoveChildAt(r);//p的第r - 1个关键码转入ls,v不再是p的第r个孩子BTNode<T> node = v.GetChild(0);v.RemoveChildAt(0);ls.InsertChild(ls.ChildCount, node);//v的最左侧孩子过继给ls做最右侧孩子while (v.KeyCount > 0){ //v剩余的关键码和孩子,依次转入lsT key2 = v.GetKey(0);v.RemoveKeyAt(0);ls.InsertKey(ls.KeyCount, key2);BTNode<T> node2 = v.GetChild(0);v.RemoveChildAt(0);ls.InsertChild(ls.ChildCount, node2);}//release(v); //释放v}else{ //与右兄弟合并/*DSA*/// printf(" ... case 3R\n");BTNode<T> rs = p.GetChild(r + 1); //右兄弟必存在T key = p.GetKey(r);p.RemoveKeyAt(r);rs.InsertKey(0, key); p.RemoveChildAt(r);//p的第r个关键码转入rs,v不再是p的第r个孩子BTNode<T> node = v.GetChild(v.ChildCount - 1);v.RemoveChildAt(v.ChildCount - 1);rs.InsertChild(0, node);if (null != rs.GetChild(0)){rs.GetChild(0).ParentNode = rs; //v的最左侧孩子过继给ls做最右侧孩子}while (v.KeyCount > 0){ //v剩余的关键码和孩子,依次转入rsT key2 = v.GetKey(v.KeyCount - 1);v.RemoveKeyAt(v.KeyCount - 1);rs.InsertKey(0, key2);BTNode<T> node2 = v.GetChild(v.ChildCount - 1);v.RemoveChildAt(v.ChildCount - 1);rs.InsertChild(0, node2);if (null != rs.GetChild(0)){rs.GetChild(0).ParentNode = rs;}}//release(v); //释放v}SolveUnderflow(p); //上升一层,如有必要则继续分裂——至多递归O(logn)层}/// <summary>/// 层序遍历,获取所有节点,切是按照每一层节点返回/// </summary>/// <param name="node"></param>/// <returns></returns>public List<List<BTNode<T>>> TraverseLevelList(BTNode<T> node){List<List<BTNode<T>>> listResult = new List<List<BTNode<T>>>();if (null == node){return listResult;}Queue<BTNode<T>> queue = new Queue<BTNode<T>>();queue.Enqueue(node);while (queue.Count > 0){int count = queue.Count;List<BTNode<T>> list = new List<BTNode<T>>();while(count > 0){--count;node = queue.Dequeue();if (null == node){continue;}list.Add(node);for (int i = 0; i < node.ChildCount; ++i){queue.Enqueue(node.GetChild(i));}}listResult.Add(list);}return listResult;}/// <summary>/// 层序遍历,获取所有节点/// </summary>/// <param name="node"></param>/// <returns></returns>public List<BTNode<T>> TraverseLevel(BTNode<T> node){List<BTNode<T>> list = new List<BTNode<T>>();if (null == node){return list;}Queue<BTNode<T>> queue = new Queue<BTNode<T>>();queue.Enqueue(node);while (queue.Count > 0){node = queue.Dequeue();if (null == node){continue;}list.Add(node);for (int i = 0; i < node.ChildCount; ++i){queue.Enqueue(node.GetChild(i));}}return list;}}
相关文章:

B树(B-tree)
B树(B-tree) B树(B-tree)是一种自平衡的多路查找树,主要用于磁盘或其他直接存取的辅助存储设备 B树能够保持数据有序,并允许在对数时间内完成查找、插入及删除等操作 这种数据结构常被应用在数据库和文件系统的实现上 B树的特点包括: B树为…...
EelasticSearch是什么?及EelasticSearch的安装
一、概述 Elasticsearch 是一个基于 Apache Lucene 构建的开源分布式搜索引擎和分析引擎。它专为云计算环境设计,提供了一个分布式的、高可用的实时分析和搜索平台。Elasticsearch 可以处理大量数据,并且具备横向扩展能力,能够通过增加更多的…...

Python机器学习项目开发实战:如何进行语音识别
注意:本文的下载教程,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 下载教程:Python机器学习项目开发实战_语音识别_编程案例解析实例详解课程教程.pdf 在Python机器学习项目…...

2024年五一杯数学建模C题思路分析
文章目录 1 赛题思路2 比赛日期和时间3 组织机构4 建模常见问题类型4.1 分类问题4.2 优化问题4.3 预测问题4.4 评价问题 5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 比赛日期和时间 报名截止时间:2024…...
【代码】Python3|Requests 库怎么继承 Selenium 的 Headers (2024,Chrome)
本文使用的版本: Chrome 124Python 12Selenium 4.19.0 版本过旧可能会出现问题,但只要别差异太大,就可以看本文,因为本文对新老版本都有讲解。 文章目录 1 难点解析和具体思路2 注意事项2.1 PDF 资源获取时注意事项2.2 Capabiliti…...
JAVA程序设计-对象设计
无论是根据某马还是某谷的适配教程做项目时候,发现了大部分都是重复的crud,大部分只要做好笔记复习即可,但是却往往忘记了编码设计,所以这里开始复习编码设计,对象设计中,长期使用Mp的那一套导致就是Service Mapper,一套梭哈完了,这样很容易忘记基本功夫 POJO: 简单…...

蓝桥杯2024年第十五届省赛真题-R 格式
找到规律后如下,只需要用高精度加法和四舍五入(本质也是高精度加法就能做),如果没有找到规律,就得自己写高精度乘法和加法,不熟练很容易错。 //#include<bits/stdc.h> #include<iostream> #i…...
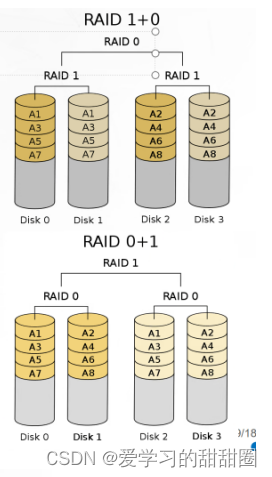
Linux服务器硬件及RAID配置
一、服务器硬件 塔式服务器:最初的服务器形态之一,类似于传统的台式电脑,但具有更强的处理能力和稳定性,适合小型企业或部门使用。 机架式服务器:设计为可安装在标准化机架内的模块化单元,可以有效地节省空…...

前端 vue单页面中请求数量过多问题 控制单页面请求并发数
需求背景: 页面中需要展示柜子,一个柜子需要调用 详情接口以及状态接口 也就是说有一个柜子就需要调用两个接口,在项目初期,接手的公司项目大概也就4-5个柜子,最多的也不超过10个,但是突然进来一个项目&a…...

HarmonyOS开发实例:【分布式手写板】
介绍 本篇Codelab使用设备管理及分布式键值数据库能力,实现多设备之间手写板应用拉起及同步书写内容的功能。操作流程: 设备连接同一无线网络,安装分布式手写板应用。进入应用,点击允许使用多设备协同,点击主页上查询…...
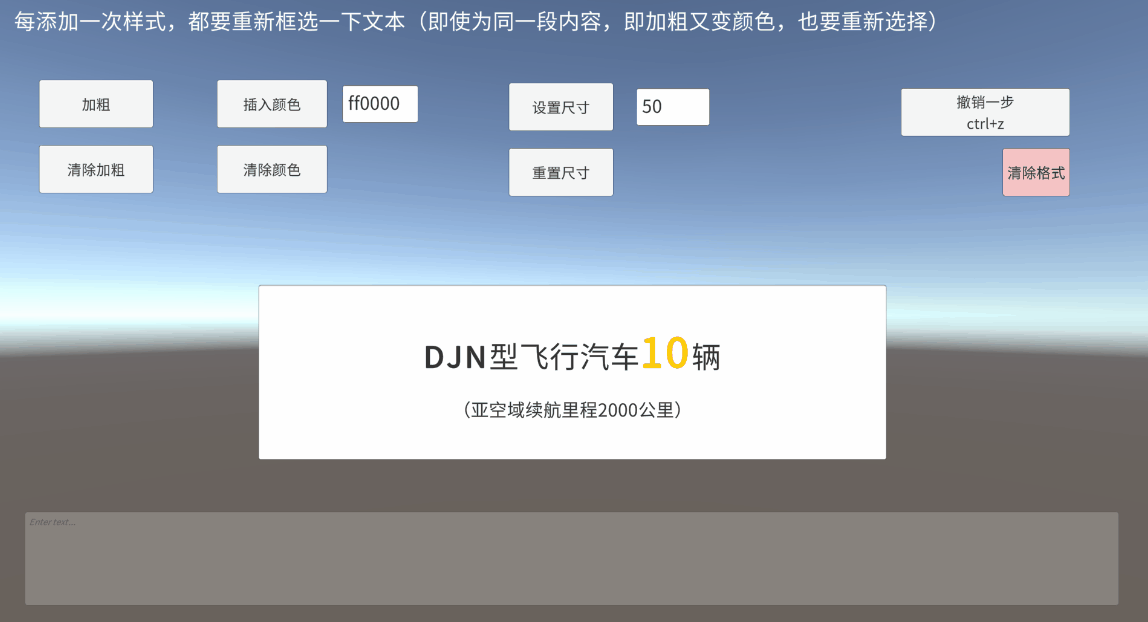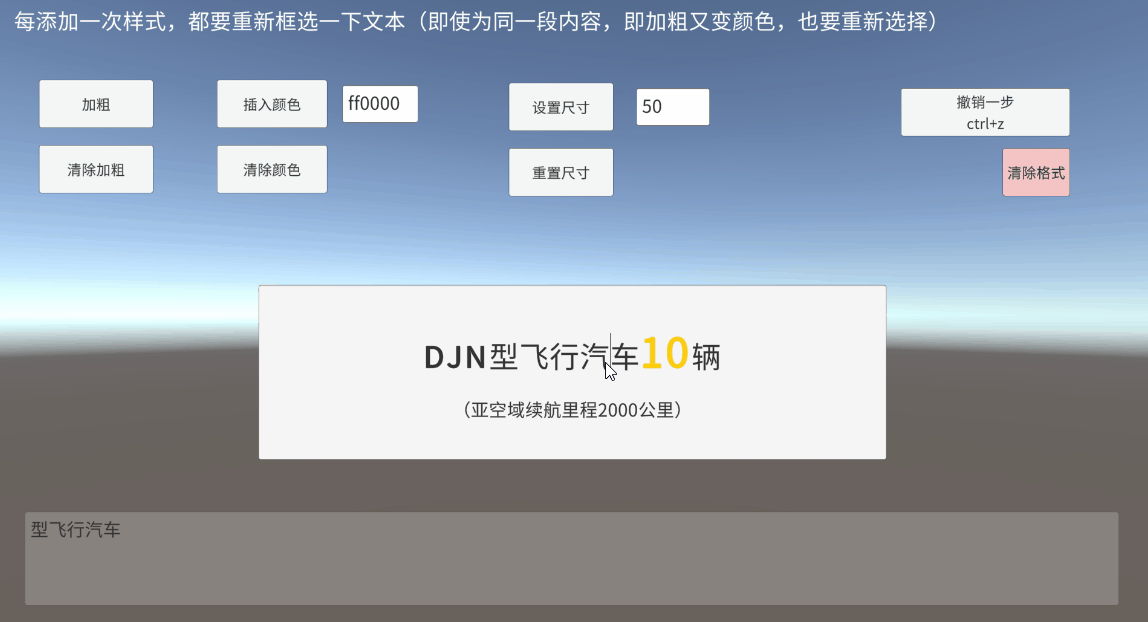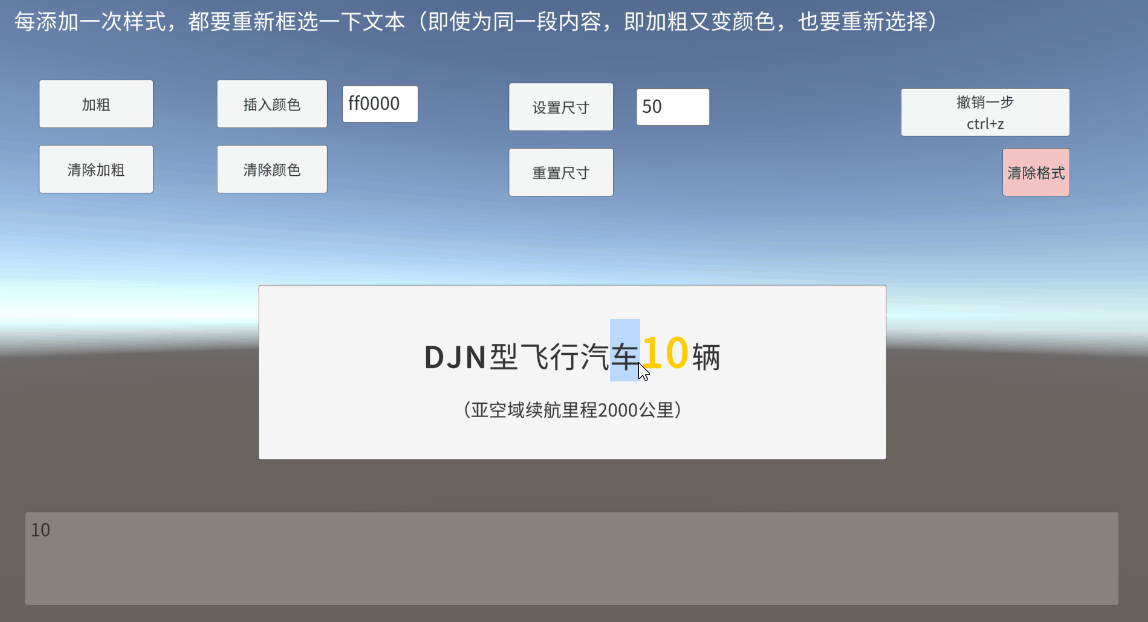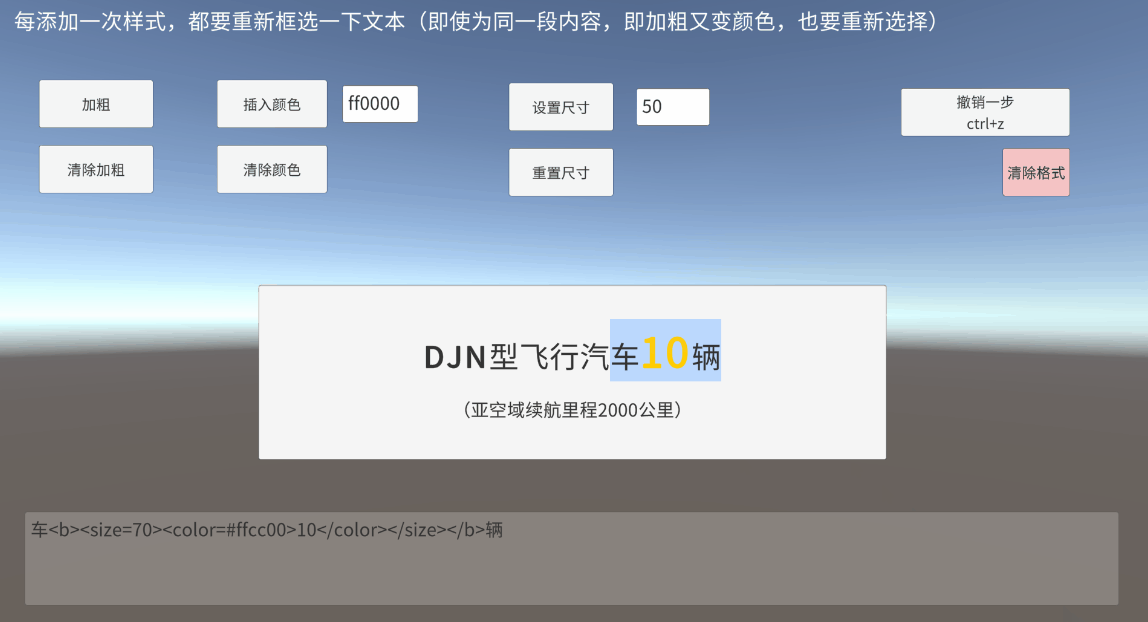
Unity TMP Inputfield 输入框 框选 富文本 获取真实定位
一、带富文本标签的框选是什么 UGUI的InputField提供了selectionAnchorPosition和selectionFocusPosition,开始选择时的光标下标和当前光标下标 对于未添加富文本标签时,直接通过以上两个值,判断一下框选方向(前向后/后向前&…...

如何在原生项目中集成flutter
两个前提条件: 从flutter v1.17版本开始,flutter module仅支持AndroidX的应用在release模式下flutter仅支持一下架构:x84_64、armeabi-v7a、arm6f4-v8a,不支持mips和x86;所以引入flutter前需要在app/build.gradle下配置flutter支持的架构 a…...

【设计模式】策略模式
目录 什么是策略模式 代码实现 什么是策略模式 策略模式是一种行为型设计模式,它定义了一系列算法,将每个算法封装成一个独立的对象,使得它们可以相互替换。 在策略模式中,通常有三个角色: 环境类(Cont…...

Java面试八股之Iterator和ListIterator的区别是什么
Iterator和ListIterator的区别是什么 这道题也是考查我们对迭代器相关的接口的了解程度,从代码中我们可以看出后者是前者的子接口,在此基础上做了一些增强,并且只用于List集合类型。 定义与基本概念 Iterator: 定义:…...
服务器中毒怎么办?企业数据安全需重视
互联网企业: 广义的互联网企业是指以计算机网络技术为基础,利用网络平台提供服务并因此获得收入的企业。广义的互联网企业可以分为:基础层互联网企业、服务层互联网企业、终端层互联网企业。 狭义的互联网企业是指在互联网上注册域名,建立网…...

k8s使用harbor私有仓库镜像 —— 筑梦之路
官方文档: Secret | Kubernetes ImagePullSecrets的设置是kubernetes机制的另一亮点,习惯于直接使用Docker Pull来拉取公共镜像,但非所有容器镜像都是公开的。此外,并不是所有的镜像仓库都允许匿名拉取,也就是说需要身份认证&…...
tcp bbr pacing 的对与错
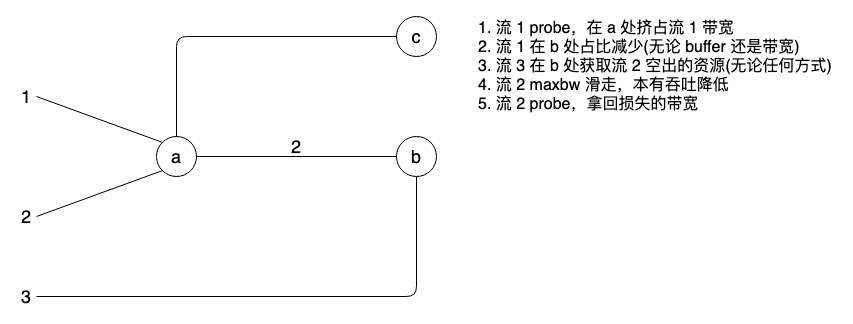
前面提到 pacing 替代 burst 是大势所趋,核心原因就是摩尔定律逐渐失效,主机带宽追平交换带宽,交换机不再能轻易吸收掉主机突发,且随着视频类流量激增,又不能以大 buffer 做带宽后备。因此,主机必须 pacing…...

MySQL学习-非事务相关的六大日志、InnoDB的三大特性以及主从复制架构
一. 六大日志 慢查询日志:记录所有执行时间超过long_query_time的查询,方便定位并优化。 # 查询当前慢查询日志状态 SHOW VARIABLES LIKE slow_query_log; #启用慢查询日志 SET GLOBAL slow_query_log ON; #设置慢查询文件位置 SET GLOBAL slow_query_log_file …...
【软件测试】MIL/HIL/PIL/SIL测试
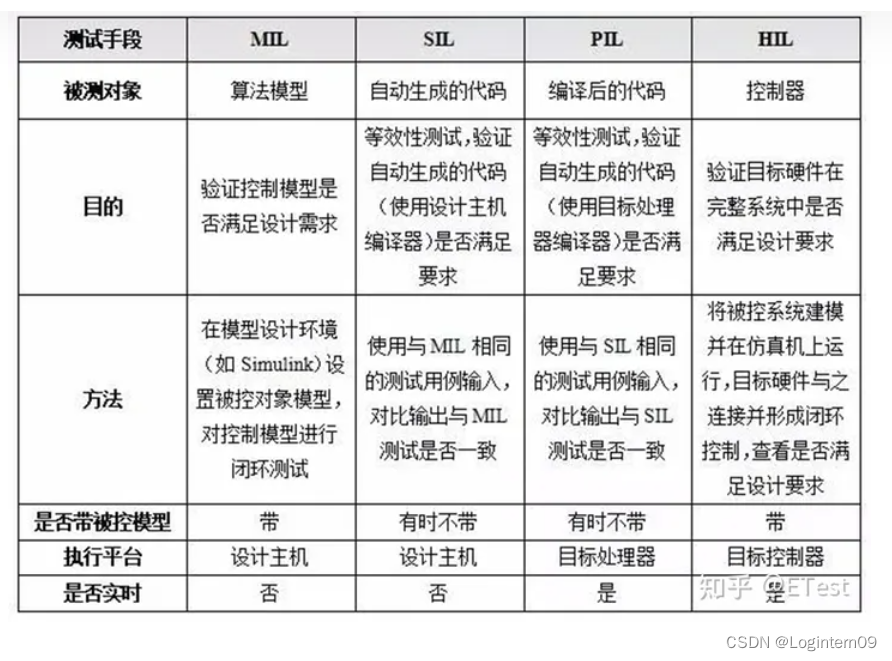
V字型开发流程 引用文章:汽车行业V模型开发详解 V模型开发(V-Model Development)是一种广泛应用于汽车行业的系统开发方法。它以字母“V”形状的图表形式展示了开发过程中不同阶段之间的关系,从需求分析到系统整合和验证&#x…...

WebKit结构深度解析:打造高效与安全的浏览器引擎
WebKit结构深度解析:打造高效与安全的浏览器引擎 在现代网络世界中,浏览器作为连接用户与互联网信息的桥梁,其背后的技术架构至关重要。WebKit,作为当今最流行的开源浏览器引擎之一,其结构设计和功能实现对于提升浏览…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
