每日OJ题_完全背包④_力扣279. 完全平方数(一维和二维)
目录
力扣279. 完全平方数
问题解析
解析代码
优化代码(相同子问题分析和滚动数组)
力扣279. 完全平方数
279. 完全平方数
难度 中等
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 10^4
class Solution {
public:int numSquares(int n) {}
};问题解析
(优化代码部分放了分析一维空间的思路,这个普通思路就简单描述了)
状态表示: dp[i][j] 表示:从前i个完全平方数中挑选,总和正好等于j,所有选法中最小的数量。
状态转移方程:
线性 dp 状态转移方程分析方式,一般都是根据最后一步的状况,来分情况讨论。但是最后一个物品能选很多个,因此需要分很多情况:
- 选 0 个i * i:dp[i][j] = dp[i - 1][j]
- 选 1 个i * i:dp[i][j] = dp[i - 1][j - i * i] + 1 ;
- 选 2 个i * i:dp[i][j] = dp[i - 1][j - 2 * i * i] + 2 ;
- ......
综上,状态转移方程为:
dp[i][j] = min(dp[i - 1][j] , dp[i - 1][j - i * i] + 1 + dp[i - 1][j - 2 * i * i] + 2 , ......)
这时发现,计算一个状态的时候,需要一个循环才能搞定的时候,我们要想到去优化。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
发现第二维是有规律的变化的,因此去看看 dp[i][j - i * i] + 1 ; 这个状态: dp[i][j - i * i] + 1 = min( dp[i - 1][j - 2 * i * i] + 2 , dp[i - 1][j - 3 * i * i] + 3 , ......)
因此可以修改我们的状态转移方程为: dp[i][j] = min(dp[i - 1][j] , dp[i][j - i * i] + 1。(j >= i * i )。有个技巧,就是相当于把第二种情况 dp[i - 1][j - i * i] + 1 里面的 i - 1 变成 i 即可。
初始化: 初始化第一行即可,dp[0[0]为1,第一行后面初始化成无穷大。
填表顺序: 根据状态转移方程,仅需从上往下填表。
返回值: 根据状态表示,返回 dp[根号n][n] 。
解析代码
class Solution {
public:int change(int amount, vector<int>& coins) {int n = coins.size();vector<int> dp(amount + 1, 0); // 滚动数组优化dp[0] = 1;for(int i = 1; i <= n; ++i){for(int j = coins[i - 1]; j <= amount; ++j){dp[j] = dp[j] + dp[j - coins[i - 1]];}}return dp[amount];}
};优化代码(相同子问题分析和滚动数组)
先看能不能将问题转化成我们熟悉的题型。这里给出一个用拆分出相同子问题的方式,定义一个状态表示。(得到的结果 i 和 j 换一下就是滚动数组优化的结果)
为了叙述方便,把和为 n 的完全平方数的最少数量简称为最小数量。
对于 12 这个数,分析一下如何求它的最小数量。
- 如果 12 本身就是完全平方数,就不用算了,直接返回 1 ;
- 但是 12 不是完全平方数,试着把问题分解⼀下:
- 情况一:拆出来一个 1 ,然后看看 11 的最小数量,记为 x1 ;
- 情况二:拆出来一个 4 ,然后看看 8 的最小数量,记为 x2 ;(为什么拆出来 4 , 而不拆出来 2 呢?)
- 情况三:拆出来一个 8 ...... 其中,接下来求 11、8 的时候,其实又回到了原来的问题上。
因此,可以尝试用 dp 的策略,将 1 2 3 4 6 等等这些数的最小数量依次保存起来。再求较大的 n 的时候,直接查表,然后找出最小数量。
状态表示: dp[i] 表示:和为 i 的完全平方数的最少数量。
状态转移方程:
对于 dp[i] ,根据思路里的分析知道,可以根据小于等于 i 的所有完全平方数 x 进行划分:
- x = 1 时,最小数量为: 1 + dp[i - 1] ;
- x = 4 时,最小数量为: 1 + dp[i - 4] ......
为了方便枚举完全平方数,采用的策略: for(int j = 1; j * j <= i; j++)
综上,状态转移方程为:
dp[i] = min(dp[i], dp[i - j * j] + 1)
初始化:当 n = 0 的时候,没法拆分,结果为 0 ; 当 n = 1 的时候,结果为 1 。
填表顺序: 根据状态转移方程,仅需从左往右填表。
返回值: 根据状态表示,返回 dp[n] 。
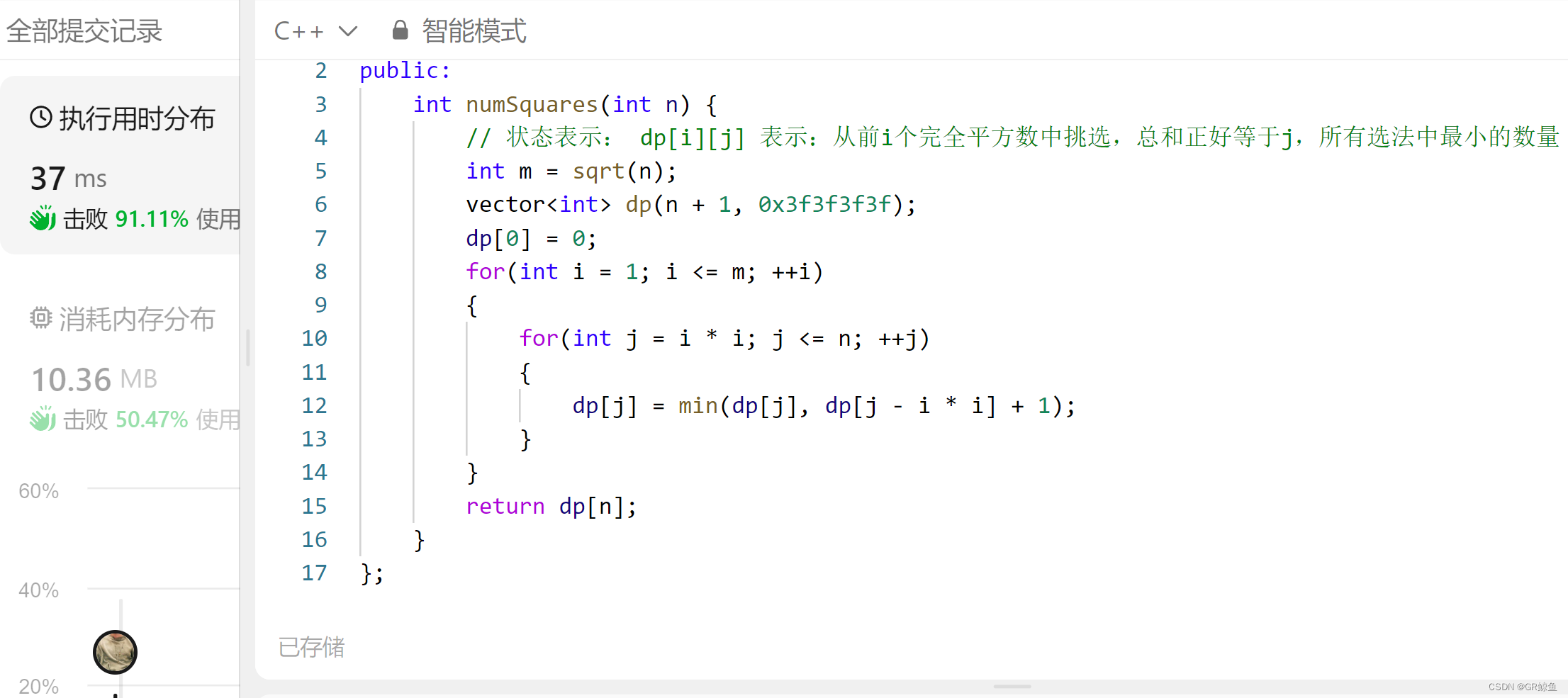
class Solution {
public:int numSquares(int n) {// dp[i] 表示:和为 i 的完全平方数的最少数量int m = sqrt(n);vector<int> dp(n + 1, 0x3f3f3f3f);dp[0] = 0;for(int i = 1; i <= m; ++i){for(int j = i * i; j <= n; ++j){dp[j] = min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
};
相关文章:

每日OJ题_完全背包④_力扣279. 完全平方数(一维和二维)
目录 力扣279. 完全平方数 问题解析 解析代码 优化代码(相同子问题分析和滚动数组) 力扣279. 完全平方数 279. 完全平方数 难度 中等 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值…...
web项目中jsp页面不识别el表达式
如果使用el表达式出现下图问题 ** 解决办法 ** 这是因为maven创建项目时,web.xml头部声明默认是2.3,这个默认jsp关闭el表达式 修改web.xml文件开头的web-app的版本 <?xml version"1.0" encoding"UTF-8"?> <web-app x…...

【Python基础】字典
文章目录 [toc]什么是字典键值对示例键异常 遍历列表什么是遍历遍历字典的键keys()方法 遍历字典的值values()方法 遍历字典的键值对items()方法 字典操作增加键值对修改键值对查询键值对get()方法 删除键值对delclear()方法 个人主页:丷从心 系列专栏:…...
2024HW --> 安全产品 Powershell无文件落地攻击
在HW中,除了了解中间件,web漏洞,这些攻击的手法,还得了解应急响应,安全产品,入侵排查,溯源反制...... 那么今天,就来说一下安全产品(安全公司我就不说了,这个…...

力扣哈哈哈哈
public class MyStack {int top;Queue<Integer> q1;Queue<Integer> q2;public MyStack() {q1new LinkedList<Integer>();q2new LinkedList<Integer>();}public void push(int x) {q2.offer(x);//offer是入队方法while (!q1.isEmpty()){q2.offer(q1.pol…...
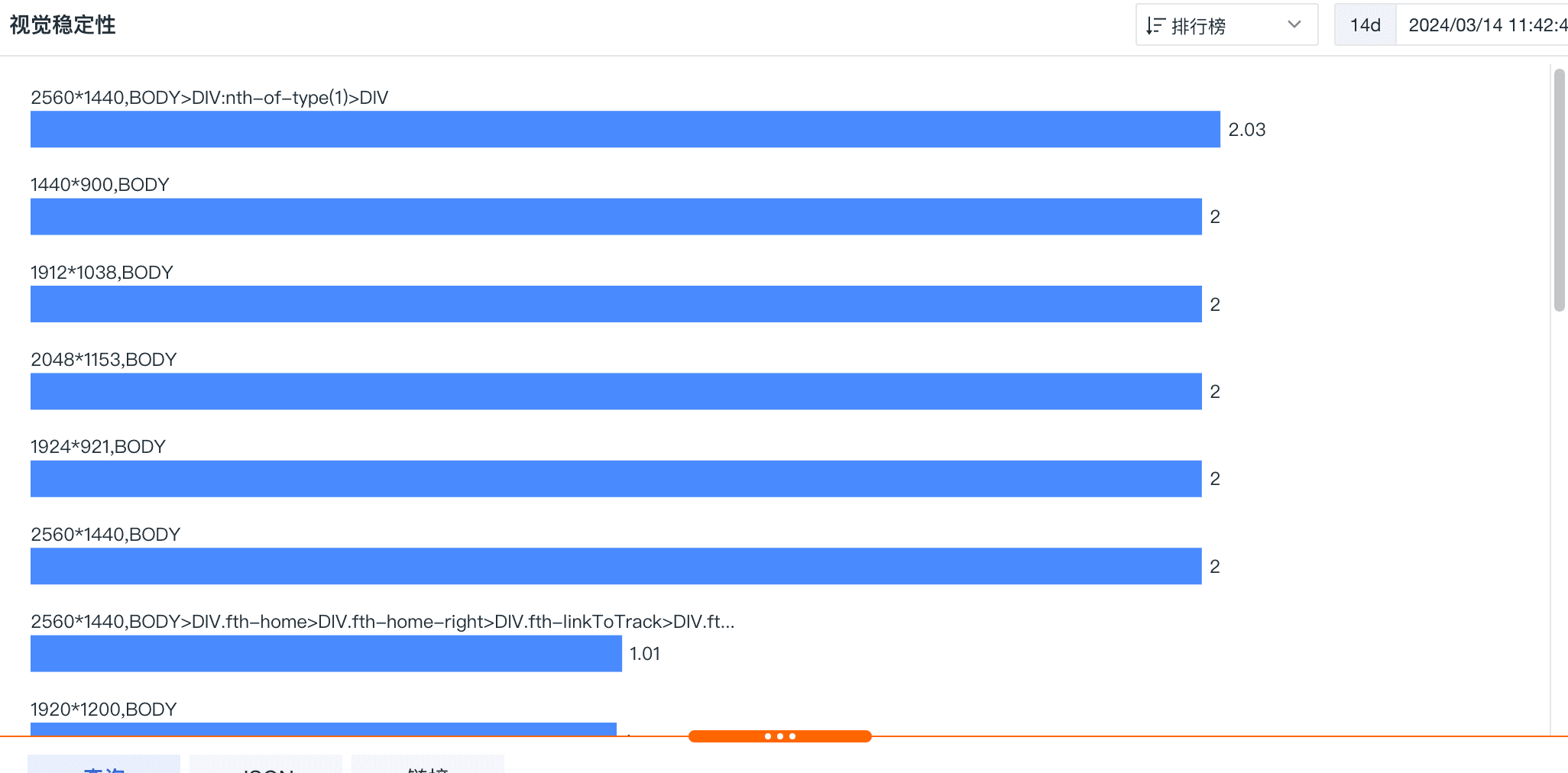
RUM 最佳实践-视觉稳定性的探索与实践
写在前面的话 在当今数字时代,网页的视觉稳定性对于提供良好的用户体验至关重要。其中一个衡量视觉稳定性的关键指标就是累积布局偏移(Cumulative Layout Shift,简称 CLS)。CLS 作为 Web Vitals 指标之一,它衡量的是网…...
PostgreSQL的学习心得和知识总结(一百三十八)|深入理解PostgreSQL数据库之Protocol message构造和解析逻辑
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...

爬虫开发教程
一、爬虫概述 爬虫(也称为网络爬虫或蜘蛛)是一种自动化程序,能够模拟人类在互联网上浏览和抓取数据的行为。它通过发送HTTP请求,获取网页的HTML代码,然后解析这些代码以提取有用的数据。爬虫在数据分析、价格监测、竞…...
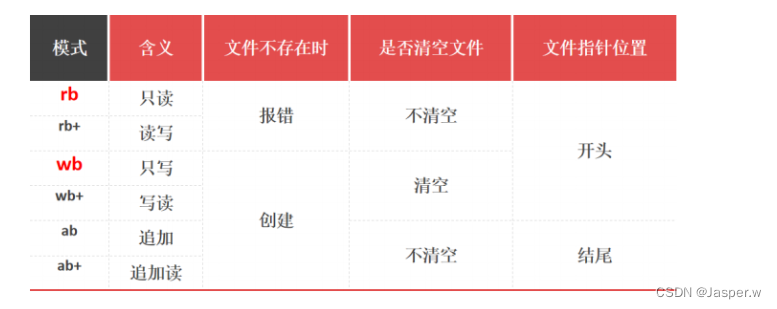
【Python】高级进阶(专版提升3)
Python 1 程序结构1.1 模块 Module1.1.1 定义1.1.2 作用1.1.3 导入1.1.3.1 import1.1.3.2 from import 1.1.4 模块变量1.1.5 加载过程1.1.6 分类 1.2 包package1.2.1 定义1.2.2 作用1.2.3 导入1.1.3.1 import1.1.3.2 from import 2 异常处理Error2.1 异常2.2 处理 3 迭代3.1 可…...

LeetCode 1378、1277、2944
1378 二级排序,compare函数必须是static的 class Solution { public:struct node {int val;int priority;};static bool compare(const node &n1, const node &n2) {if (n1.priority n2.priority) {return n1.val < n2.val;}return n1.priority < n…...
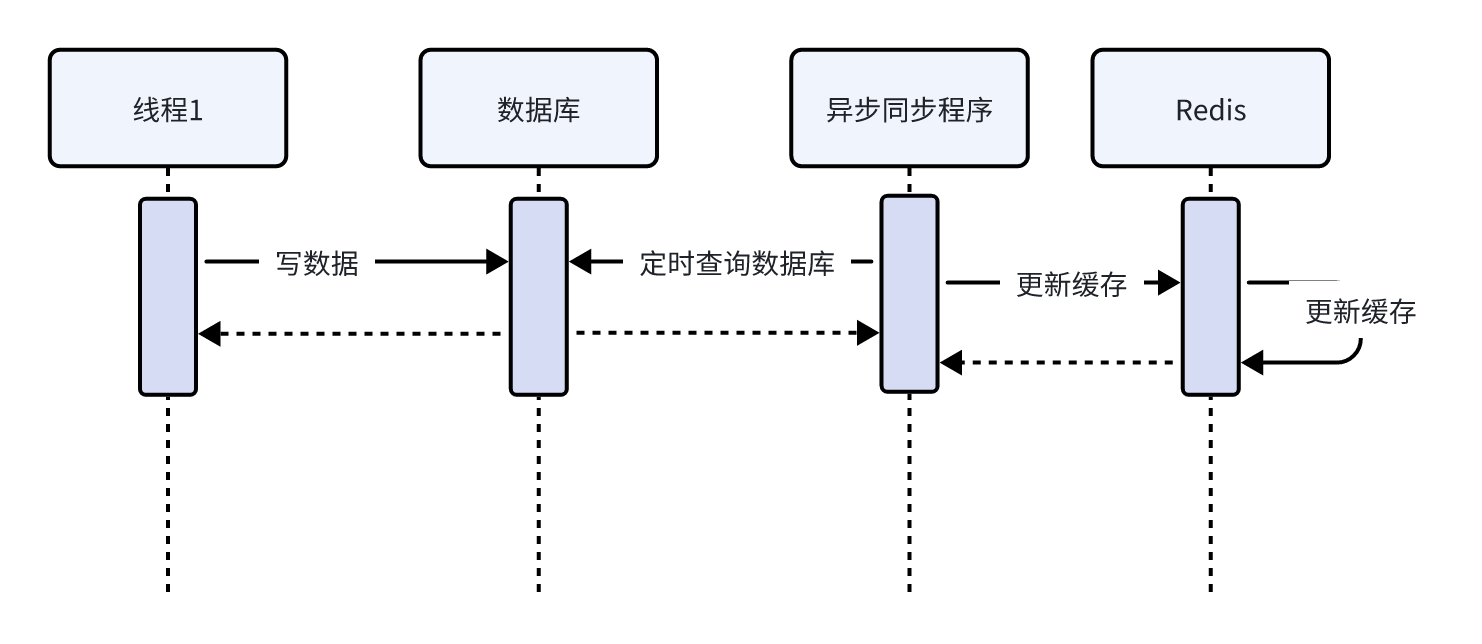
【缓存常见问题】
在使用缓存时特别是在高并发场景下会遇到很多问题,常用的问题有缓存穿透、缓存击穿、缓存雪崩以及缓存一致性问题。 1、缓存穿透 首先,什么是缓存穿透呢? 缓存穿透是指请求一个不存在的数据,缓存层和数据库层都没有这个数据&…...

Python爬取猫眼电影票房 + 数据可视化
目录 主角查看与分析 爬取可视化分析猫眼电影上座率前10分析猫眼电影票房场均人次前10分析猫眼电影票票房占比分析 主角查看与分析 爬取 对猫眼电影票房进行爬取,首先我们打开猫眼 接着我们想要进行数据抓包,就要看网站的具体内容,通过按F12…...

Spring Boot深度解析:是什么、为何使用及其优势所在
在Java企业级应用开发的漫长历史中,Spring框架以其卓越的依赖注入和面向切面编程的能力,赢得了广大开发者的青睐。然而,随着技术的不断进步和项目的日益复杂,传统的Spring应用开发流程逐渐显得繁琐和低效。为了解决这一问题&#…...

面向对象——类与对象
文章目录 类与对象构造函数、析构函数get/set方法函数:类内声明、类外定义static 类与对象 #include<iostream> #include<string> using namespace std; /* 类与对象 */ class Person{public:string name;// 固有属性,成员变量 int age;pu…...

Golang的[]interface{}为什么不能接收[]int?
在 Go 中,[]interface{} 和 []int 是两种不同的类型,虽然它们的底层数据结构都是切片,但是它们的元素类型不同。[]interface{} 是一个空接口切片,可以容纳任意类型的元素,而 []int 是一个整数切片,只能容纳…...
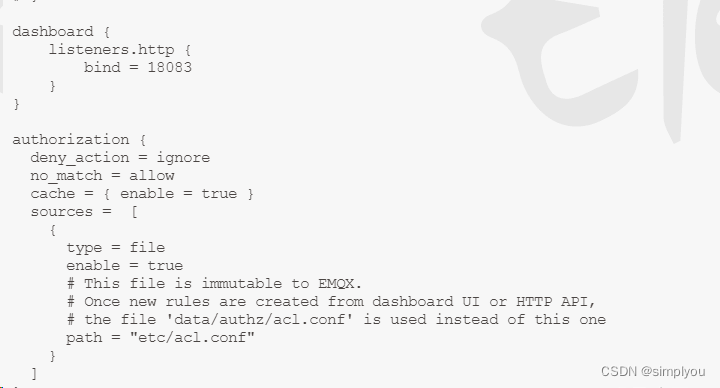
重启服务器或重启docker,导致emqx的Dashboard的密码重置为public
最近在项目中突然发现重启服务器,或者重启docker 修改好的emqx的Dashboard的密码重置为public 技术博客 http://idea.coderyj.com/ 1.解决办法就是固定 emqx的节点 # 拉取镜像 docker pull emqx/emqx# 创建目录,进行目录挂载 mkdir -p /docker/emqx/{etc,lib,data,…...

就业班 第三阶段(ansible) 2401--4.16 day2 ansible2 剧本+角色
六、Ansible playbook 简介 playbook 是 ansible 用于配置,部署,和管理被控节点的剧本。 通过 playbook 的详细描述,执行其中的一系列 tasks ,可以让远端主机达到预期的状态。playbook 就像 Ansible 控制器给被控节点列出的的…...

常用的过滤网站扫描网站攻击的路径是那些,比如:/etc/passwd等
网站攻击中经常被尝试的路径主要包括利用漏洞获取敏感文件、执行系统命令或者注入恶意代码的尝试。以下是一些常见的被攻击者尝试访问的路径和文件,这些通常在网络入侵检测系统(IDS)和网络防火墙的过滤规则中被特别关注: 系统文件…...
考研数学|《1800》《660》《880》如何选择和搭配?(附资料分享)
直接说结论:基础不好先做1800、强化之前660,强化可选880/1000题。 首先,传统习题册存在的一个问题是题量较大,但难度波动较大。《汤家凤1800》和《张宇1000》题量庞大,但有些题目难度不够平衡,有些过于简单…...

论文笔记:Are Human-generated Demonstrations Necessary for In-context Learning?
iclr 2024 reviewer 评分 6668 1 intro 大型语言模型(LLMs)已显示出在上下文中学习的能力 给定几个带注释的示例作为演示,LLMs 能够为新的测试输入生成输出然而,现行的上下文学习(ICL)范式仍存在以下明显…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
