供应链|经典论文解读:(s,S) 策略在动态库存下的最优性

文章考虑了具有订购成本(由单位成本加上重新订购成本组成)的动态库存问题。具体而言,对于每个时期,系统在中期开始是做出一系列采购决策——这些采购有助于库存的积累,并在随后的周期被需求所消耗。每时期系统会产生各种成本,一般包括:采购或订购成本 c ( z ) c(z) c(z),其中 z z z是购买量;持有成本 h ( ⋅ ) h(\cdot) h(⋅),为时期末供应量超过需求量的函数;以及缺货成本 p ( ⋅ ) p(\cdot) p(⋅),为周期末需求量超过供应量的函数。每个时期结束时会计算持有成本或缺货成本,而订购成本则在进行采购时计算。库存问题的目标便是选择采购决策以最小化所有成本的折现值的期望。文章在最初假设采购仅在周期开始时进行,并且交货是即时的;后续将假设拓展考虑延迟交货的情况。
设交货后的库存水平立即为 y y y,则该周期内将收取的预期持有和缺货成本为 L ( y ) L(y) L(y):
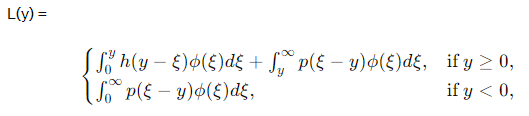
其中 φ \varphi φ是需求分布的密度函数。若考虑 n n n个时期、初始库存为 x x x的库存问题,令 C n ( x ) C_n(x) Cn(x)表示在最优配给下 n n n个时期计划的折现成本的期望值(折现因子 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1])。则可得出 C n ( x ) C_n(x) Cn(x):
C n ( x ) = min y ≥ x { c ( y − x ) + L ( y ) + α ∫ 0 ∞ C n − 1 ( y − ξ ) φ ( ξ ) d ξ } , C_n(x)=\min_{y\geq x}\{c(y-x)+L(y)+\alpha\int_0^{\infty}C_{n-1}(y-\xi)\varphi(\xi)\mathrm{d}\xi\}, Cn(x)=y≥xmin{c(y−x)+L(y)+α∫0∞Cn−1(y−ξ)φ(ξ)dξ},
如果 y n ( x ) y_n(x) yn(x)为最优解,则 y n ( x ) − x y_n(x)-x yn(x)−x表示最优的初始购买量。
文章证明,如果持有成本和缺货成本是线性的,则每个时期中的最优策略总是 (s, S) 类型。
首先回顾单时期问题,即 n = 1 n=1 n=1且 C 0 ≡ 0 C_0\equiv 0 C0≡0, 而单时期问题本质上是一个微积分问题。
- 最简单的情况是订购成本是线性的,即 c ( z ) = c ⋅ z c(z)=c\cdot z c(z)=c⋅z. 在这种情况下,单时期模型的最优策略通常由单个临界数 x ˉ \bar{x} xˉ定义如下:如果 x < x ˉ x<\bar{x} x<xˉ,则购买 x ˉ − x \bar{x}-x xˉ−x;如果 x > x ˉ x>\bar{x} x>xˉ,则不购买。在多时期问题中,类似的结果通常成立,最优策略由一系列临界数 x ˉ 1 , x ˉ 2 , ⋯ \bar{x}_1,\bar{x}_2,\cdots xˉ1,xˉ2,⋯定义。这些结果成立的充分条件是 L ( y ) L(y) L(y)是凸的,而这一条件在持有和短缺成本均为原点处消失的凸递增函数时成立。
- 当订购成本不再是线性时,文章集中讨论了最简单类型的非线性成本:
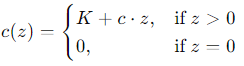
其中 K K K通常被描述为固定订购成本。在该订购成本下,单时期模型中的最优策略通常由一对临界数 (s, S) 定义:如果$ x<s $,则订购 ( S − x ) (S-x) (S−x);如果$ x>s ,则不订购。在单时期模型中有一些示例显示这样的策略并非最优。然而,如果持有和短缺成本为线性函数 ,则不订购。在单时期模型中有一些示例显示这样的策略并非最优。然而,如果持有和短缺成本为线性函数 ,则不订购。在单时期模型中有一些示例显示这样的策略并非最优。然而,如果持有和短缺成本为线性函数h(u)=h\cdot u 和 和 和p(u)=p\cdot u , 或者更一般地,如果 , 或者更一般地,如果 ,或者更一般地,如果L(y)$是凸的,那么多时期模型的最优策略是 (s, S).
然而,即使假设持有和短缺成本是线性的,在原文章发表的60年代前,关于动态模型最优策略的文献也非常少。Bratten
表示(引用章节9),如果需求的密度是递减的,动态模型的最优策略是由一系列临界数对 ( s 1 , S 1 s_1, S_1 s1,S1), ( s 2 , S 2 s_2, S_2 s2,S2),… 定义。唯一的另一种结果由 Karlin提出,即如果 φ \varphi φ有一个单调似然比,当持有和缺货成本是线性的,且 c + h > α p c+h>\alpha p c+h>αp,那么最优策略也是同样的类型。这两个结果都相当限制性,前者要求一个递减的密度,后者对成本有严格的约束。
而文章证明了,如果持有成本和缺货成本是线性的,或更一般地,当 L ( y ) L(y) L(y)是凸的并且订购成本如上非线性时,则每个时期中的最优策略总是 (s, S) 类型,无需任何附加条件。
上述两个结果的推导基于对函数 G n ( y ) G_n(y) Gn(y)的研究,其中
G n ( y ) = c y + L ( y ) + α ∫ 0 ∞ C n − 1 ( y − ξ ) φ ( ξ ) d ξ , G_n(y)=cy+L(y)+\alpha\int_0^{\infty}C_{n-1}(y-\xi)\varphi(\xi)\mathrm{d}\xi, Gn(y)=cy+L(y)+α∫0∞Cn−1(y−ξ)φ(ξ)dξ,
当且仅当 存在 y > x y>x y>x, G n ( x ) > K + G n ( y ) G_n(x)>K+G_n(y) Gn(x)>K+Gn(y), 从 x x x订购是最优的;若要求从 x x x订购,则订购到 使 G n ( y ) G_n(y) Gn(y)最小的 y y y ( y > x ) (y>x) (y>x). 当假设 Bratten 的条件或 Karlin 的条件时, G n ( y ) G_n(y) Gn(y)递减到一个最小值然后再递增。现将最小满足情况的 y y y记作 S n S_n Sn且定义 s n s_n sn:
G n ( s n ) = G n ( S n ) + K , G_n(s_n)=G_n(S_n)+K, Gn(sn)=Gn(Sn)+K,
则由 ( s n , S n s_n,S_n sn,Sn) 定义的策略是最优的。然而,少量的数值计算就足以显示函数 G n G_n Gn并不总是符合次规律——实际上,可能有许多极大值和极小值。文章给出的证明思路是,尽管 G n G_n Gn可能有很多极大值和极小值,但其变化不会致使导致偏离 (s,S) 策略。
如果 L ( y ) L(y) L(y)是凸的,对于任一 a ≥ 0 a\geq 0 a≥0, 则 K + G n ( a + x ) − G n ( x ) − a G n ′ ( x ) ≥ 0 K+G_n(a+x)-G_n(x)-aG'_n(x)\geq 0 K+Gn(a+x)−Gn(x)−aGn′(x)≥0.
文章分情况讨论了即时与延时交货的情况来证明上述不等式的成立。假设 G n ( x ) G_n(x) Gn(x)的变化如图1所示:系统会在区间 I 订购到点 S S S,在区间 II 不订购,在区间 III 订购到 S S S,在区间 IV 不订购,在区间 V 订购到 S ′ S' S′,在区间 VI 不订购。但若以上不等式成立,则该曲线不能成立:若有让 x + a = S x+a=S x+a=S并且 x x x是在 III 中达到相对最大值的点,而对于这个值的 x x x, G n ′ = 0 G'_n=0 Gn′=0并且以上不等式意味着 K + G n ( x ) − G n ( x ) ≥ 0 K+G_n(x)-G_n(x)\geq 0 K+Gn(x)−Gn(x)≥0,这与图1矛盾。同样的论证可以应用于点 S ′ S' S′. 接下来针对订购货物到达的时间分情况讨论。
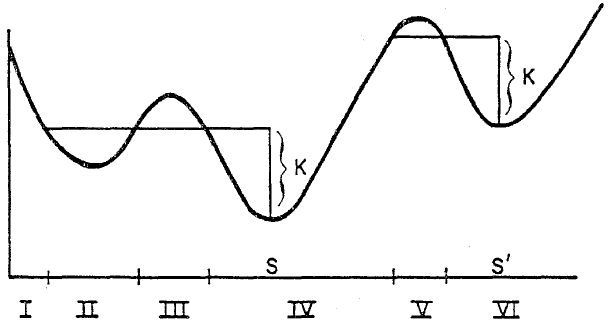
图1. 在假设的订购方案下的期望成本变化
零交货延迟的情况
对于即时交货的情况,文章提出以下定义:
设 K ≥ 0 K\geq 0 K≥0并且 f ( x ) f(x) f(x)是一个可微分函数。如果对于所有 a > 0 a>0 a>0和所有 x x x,有
K + f ( a + x ) − f ( x ) − a f ′ ( x ) ≥ 0 , K+f(a+x)-f(x)-af'(x)\geq 0, K+f(a+x)−f(x)−af′(x)≥0,
则称 f ( x ) f(x) f(x)是 K-凸的。如果不假设可微分性,则 K-凸性的定义为
K + f ( a + x ) − f ( x ) − a [ f ( x + b ) − f ( x ) b ] ≥ 0. K+f(a+x)-f(x)-a[\frac{f(x+b)-f(x)}{b}]\geq 0. K+f(a+x)−f(x)−a[bf(x+b)−f(x)]≥0.
K-凸函数的简单属性包括:
- 0-凸性等同于普通凸性。
- 如果 f ( x ) f(x) f(x)是 K-凸的,那么对于所有 h h h, f ( x + h ) f(x+h) f(x+h)也是 K-凸的。
- 如果 f f f和 g g g分别是 K-凸和 M-凸的,且有 α \alpha α 和 β \beta β为正,那么 α f + β g \alpha f+\beta g αf+βg是 ( α K + β M ) (\alpha K+\beta M) (αK+βM)-凸的。
运用数学归纳法,首先, G 1 ( x ) = c x + L ( x ) G_1(x) = cx+L(x) G1(x)=cx+L(x)显然是 K-凸的(0-凸)。
其次,假设 G 2 , … , G n G_2,\ldots,G_n G2,…,Gn也是 K-凸的。根据 G n ( x ) G_n(x) Gn(x)的定义,为证明 G n + 1 ( x ) G_{n+1}(x) Gn+1(x)的 K-凸性,则只需证明 ∫ 0 ∞ C n ( x − ξ ) φ ( ξ ) d ξ \int_{0}^{\infty}C_n(x-\xi)\varphi(\xi)\mathrm{d}\xi ∫0∞Cn(x−ξ)φ(ξ)dξ是 K-凸的,而通过上述属性2和3,足够证明 C n ( x ) C_n(x) Cn(x)是 K-凸的,推导如下。
首先,如果 S n S_n Sn是 G n ( x ) G_n(x) Gn(x)的绝对最小值,并且已定义 s n s_n sn为满足 K + G n ( S n ) = G n ( s n ) K+G_n(S_n)=G_n(s_n) K+Gn(Sn)=Gn(sn)的$ x<S_n ,那么最优策略是:当 ,那么最优策略是:当 ,那么最优策略是:当 x<s_n 则订购到 则订购到 则订购到S_n$,否则不订购。因此,
- 当$ x<s_n 时, 时, 时,C_n(x)=K+c(S_n-x)+C_n(S_n)=K-cx+G_n(S_n)$;
- 当$ x>s_n 时, 时, 时,C_n(x) = -cx+G_n(x)$.
情况 1: x > s n x>s_n x>sn. 在这个区域, C n ( x ) C_n(x) Cn(x)等于线性函数加上K-凸函数,因此是 K-凸的。
情况 2:$ x<s_n<x+a $. 在这种情况下,
K + C n ( x + a ) − C n ( x ) − a C n ′ ( x ) = K + C n ( x + a ) − C n ( x ) + a c K+C_n(x+a)-C_n(x)-aC'_n(x)=K+C_n(x+a)-C_n(x)+ac K+Cn(x+a)−Cn(x)−aCn′(x)=K+Cn(x+a)−Cn(x)+ac
为正,因为
C n ( x ) = min y > x { K + c ( y − x ) + L ( y ) + α ∫ 0 ∞ C n − 1 ( y − ξ ) φ ( ξ ) d ξ } C_n(x)=\min_{y>x}\{K+c(y-x)+L(y)+\alpha\int_0^{\infty}C_{n-1}(y-\xi)\varphi(\xi)\mathrm{d}\xi\} Cn(x)=y>xmin{K+c(y−x)+L(y)+α∫0∞Cn−1(y−ξ)φ(ξ)dξ}
≤ K + c a + K ( x + a ) + α ∫ 0 ∞ C n − 1 ( x + a − ξ ) φ ( ξ ) d ξ \leq K+ca +K(x+a)+\alpha\int_0^{\infty}C_{n-1}(x+a-\xi)\varphi(\xi)\mathrm{d}\xi ≤K+ca+K(x+a)+α∫0∞Cn−1(x+a−ξ)φ(ξ)dξ
= K + c a + C n ( x + a ) . =K+ca+C_n(x+a). =K+ca+Cn(x+a).
情况 3:$ x + a < s_n . 在这个区域, . 在这个区域, .在这个区域, C_n(x) $是线性的,因此是 K-凸的。归纳完成,并证明了在这一部分考虑的情况下 (s, S) 策略的最优性。
交货延迟的情况
当存在交货延迟时,最优策略的性质很大程度上取决于是超额需求被积压还是被加急处理。如果超额需求被积压,那么已知最优策略是现有库存加上已订购但尚未交付的库存的函数;如果超额需求被加急处理,最优策略则将复杂得多——文章仅考虑积压为满足需求的情况。
令交货延迟记作 λ \lambda λ,即在时期开始时下的订单在 λ \lambda λ个时期后的开始时交付。考虑 n n n个时期,令 x x x表示当前库存, x 1 x_1 x1表示下个时期开始时要交付的库存, x j x_j xj表示 j j j个时期后交付的库存,其中 j = 1 , 2 , … , λ − 1 j=1,2,\ldots,\lambda-1 j=1,2,…,λ−1. 令 C n ( x , x 1 , … , x λ − 1 ) C_n(x,x_1,\ldots,x_{\lambda-1}) Cn(x,x1,…,xλ−1)表示最小期望成本,则
C n ( x , x 1 , … , x λ − 1 ) = min z ≥ 0 { c ( z ) + L ( x ) + α ∫ − ∞ C n − 1 ( x + x 1 − ξ , x 2 , … , z ) φ ( ξ ) d ξ } . C_n(x,x_1,\ldots,x_{\lambda-1})=\min_{z\geq 0}\{c(z)+L(x)+\alpha\int_-^{\infty}C_{n-1}(x+x_1-\xi,x_2,\ldots,z)\varphi(\xi)\mathrm{d}\xi\}. Cn(x,x1,…,xλ−1)=z≥0min{c(z)+L(x)+α∫−∞Cn−1(x+x1−ξ,x2,…,z)φ(ξ)dξ}.
接下来将证明,如 L ( x ) L(x) L(x)是凸的,并且购买成本如前文所示非线性,最优策略可由 S n S_n Sn和 s n s_n sn描述:如果$ x+x_1+\ldots +x_{\lambda-1}>s_n 则不订购;如果 则不订购;如果 则不订购;如果 x+x_1+\ldots +x_{\lambda-1}<s_n 则订购到 则订购到 则订购到S_n$.
根据 C n ( x , x 1 , … , x λ − 1 ) C_n(x,x_1,\ldots,x_{\lambda-1}) Cn(x,x1,…,xλ−1)定义,对于 n ≥ λ n\geq \lambda n≥λ:
C n ( x , x 1 , x 2 , … , x λ − 1 ) C_n(x,x_1,x_2,\ldots,x_{\lambda-1}) Cn(x,x1,x2,…,xλ−1)
= L ( x ) + α ∫ 0 ∞ L ( x + x 1 − ξ ) φ ( ξ ) d ξ + ⋯ =L(x)+\alpha\int_0^{\infty}L(x+x_1-\xi)\varphi(\xi)\mathrm{d}\xi + \cdots =L(x)+α∫0∞L(x+x1−ξ)φ(ξ)dξ+⋯
+ α λ − 1 ∫ 0 ∞ ⋯ ∫ 0 ∞ L ( x + ⋯ + x λ − 1 − ∑ i = 1 λ − 1 ξ i ) φ ( ξ 1 ) ⋯ φ ( ξ λ − 1 ) d ξ ⋯ d ξ λ − 1 + f n ( x + x 1 + ⋯ + x λ − 1 ) , +\alpha^{\lambda-1}\int_0^{\infty}\cdots\int_0^{\infty}L(x+\cdots +x_{\lambda-1}-\sum_{i=1}^{\lambda-1}\xi_i)\varphi(\xi_1)\cdots\varphi(\xi_{\lambda-1})\mathrm{d}\xi\cdots\mathrm{d}\xi_{\lambda-1} +f_n(x+x_1+\cdots+x_{\lambda-1}), +αλ−1∫0∞⋯∫0∞L(x+⋯+xλ−1−i=1∑λ−1ξi)φ(ξ1)⋯φ(ξλ−1)dξ⋯dξλ−1+fn(x+x1+⋯+xλ−1),
其中 f n ( u ) f_n(u) fn(u)满足
f n ( u ) = min x ≥ 0 { c ( z ) + α λ ∫ 0 ∞ ⋯ ∫ 0 ∞ L ( u + z − ∑ i = 1 λ ξ i ) φ ( ξ 1 ) ⋯ φ ( ξ λ ) d ξ 1 ⋯ d ξ λ } . f_n(u)=\min_{x\geq0}\{c(z)+\alpha^{\lambda}\int_0^{\infty}\cdots\int_0^{\infty}L(u+z-\sum_{i=1}^{\lambda}\xi_i)\varphi(\xi_1)\cdots\varphi(\xi_{\lambda})\mathrm{d}\xi_1\cdots\mathrm{d}\xi_{\lambda}\}. fn(u)=x≥0min{c(z)+αλ∫0∞⋯∫0∞L(u+z−i=1∑λξi)φ(ξ1)⋯φ(ξλ)dξ1⋯dξλ}.
因此若令 y = u + z y=u+z y=u+z,即相当于 L ( y ) L(y) L(y)被
α λ ∫ 0 ∞ ⋯ ∫ 0 ∞ L ( u + z − ∑ i = 1 λ ξ i ) φ ( ξ 1 ) ⋯ φ ( ξ λ ) d ξ 1 ⋯ d ξ λ } \alpha^{\lambda}\int_0^{\infty}\cdots\int_0^{\infty}L(u+z-\sum_{i=1}^{\lambda}\xi_i)\varphi(\xi_1)\cdots\varphi(\xi_{\lambda})\mathrm{d}\xi_1\cdots\mathrm{d}\xi_{\lambda}\} αλ∫0∞⋯∫0∞L(u+z−i=1∑λξi)φ(ξ1)⋯φ(ξλ)dξ1⋯dξλ}
替换。然而,如果 L ( y ) L(y) L(y)是凸的,那么替换它的上式也是凸的,这就足以完成证明。于是可以得出结论,如果持有成本和缺货成本是线性的,则每个时期中的最优策略总是 (s, S) 类型。
参考文献
ARROW, K. J., T. HARRIS, and J. MARSCHAK. “Optimal Inventory Policy,” Econometrica, 19(1951), 250-72.
ARROW, K. J., S. KARLIN, and H. SCARF. Studies in the Mathematical Theory of Inventory and Production, Stanford, Calif.: Stanford University Press, 1958.
BELLMAN, R., I. GLICKSBERG, and O. GROSS. “On the Optimal Inventory Equation,” Management Science, 2(1955), 83-104.
DVORETZKY, A., J. KIEFER, and J. WOLFOWITZ. “The Inventory Problem, I. Case of Known Distributions of Demand,” Econometrica, 20(1952), 187-222.
DVORETZKY, A., J. KIEFER, and J. WOLFOWITZ. “On the Optimal Character of the (S,s) Policy in Inventory Theory,” Econometrica, 21(1953), 586-96.
相关文章:

供应链|经典论文解读:(s,S) 策略在动态库存下的最优性
文章考虑了具有订购成本(由单位成本加上重新订购成本组成)的动态库存问题。具体而言,对于每个时期,系统在中期开始是做出一系列采购决策——这些采购有助于库存的积累,并在随后的周期被需求所消耗。每时期系统会产生各…...

Python从0到100(二十):文件读写和文件操作
一、文件的打开和关闭 有了文件系统可以非常方便的通过文件来读写数据;在Python中要实现文件操作是非常简单的。我们可以使用Python内置的open函数来打开文件,在使用open函数时,我们可以通过函数的参数指定文件名、操作模式和字符编码等信息…...
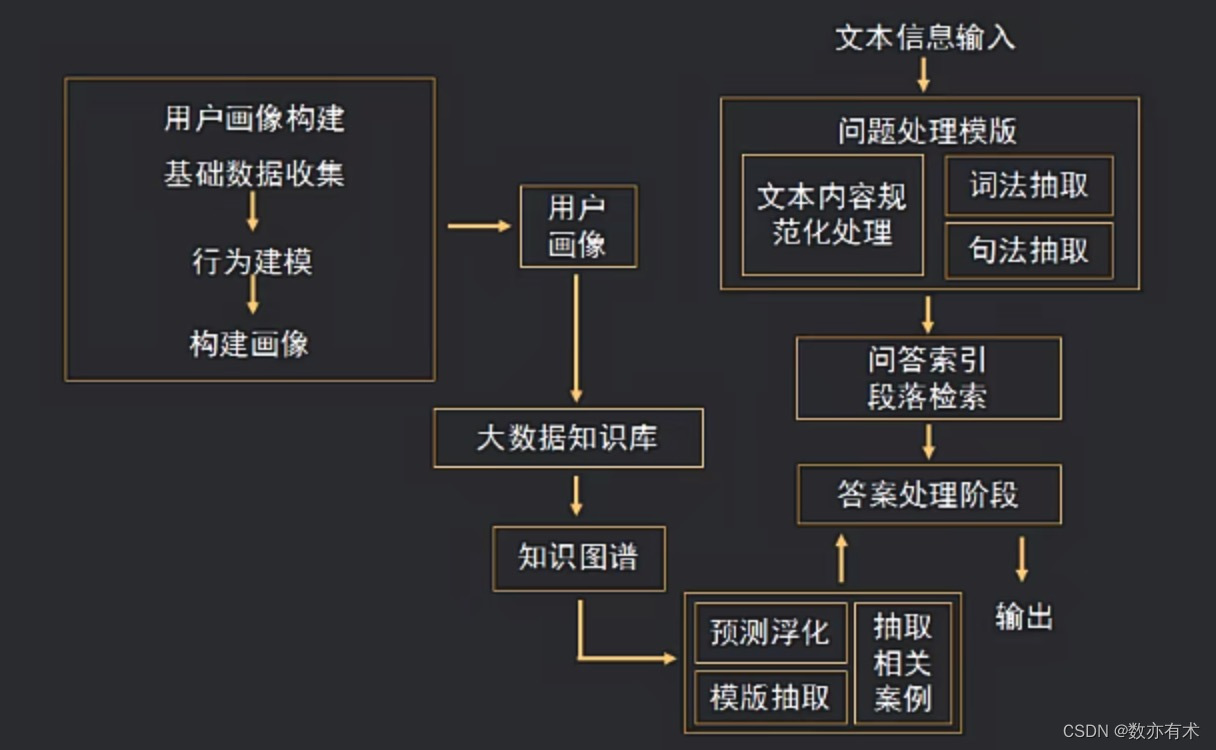
AI+客服行业落地应用
一、客服行业变迁 1.传统客服时代 (1)客服工作重复性高,技术含量低 (2)呼出效率低,客服水平参差不齐 (3)管理难度高,情绪不稳定 (4)服务质量…...
40 生产者消费者模型
生产者消费者模型 概念 为何要使用生产者消费者模型,这个是用过一个容器解决生产者和消费的强耦合问题。生产者和消费者之间不需要通讯,通过阻塞队列通讯,所以生产者生产完数据之后不用等待消费者处理,直接扔给阻塞队列…...
QT5之windowswidget_菜单栏+工具栏_核心控件_浮动窗口_模态对话框_标准对话框/文本对话框
菜单栏工具栏 新建工程基类是QMainWindow 1、 2、 3、 点.pro文件,添加配置 因为之后用到lambda; 在.pro文件添加配置c11 CONFIG c11 #不能加分号 添加头文件 #include <QMenuBar>//菜单栏的头文件 主窗口代码mainwindow.cpp文件 #include &q…...
)
Satellite, Aerial, and Underwater Communication Track(WCSP2023)
1.Dispersion Curve Extraction and Source Localization for Single Hydrophone by Combining Image Skeleton Extraction with Advanced Time-Frequency Analysis(图像骨架提取与先进时频分析相结合的单水听器色散曲线提取和源定位) 摘要:时频分析(TF…...
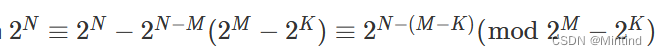
AtCoder Regular Contest 176(ARC176)A、B
题目:AtCoder Regular Contest 176 - tasks 官方题解:AtCoder Regular Contest 176 - editorial 参考:atcoder regular 176 (ARC176) A、B题解 A - 01 Matrix Again 题意 给一个nn的方格,给出m个坐标(x,y)m,在方格中…...
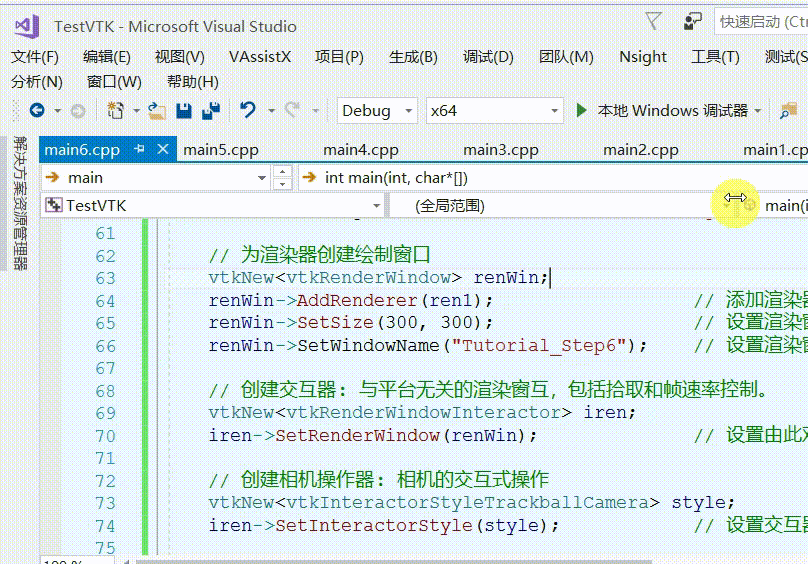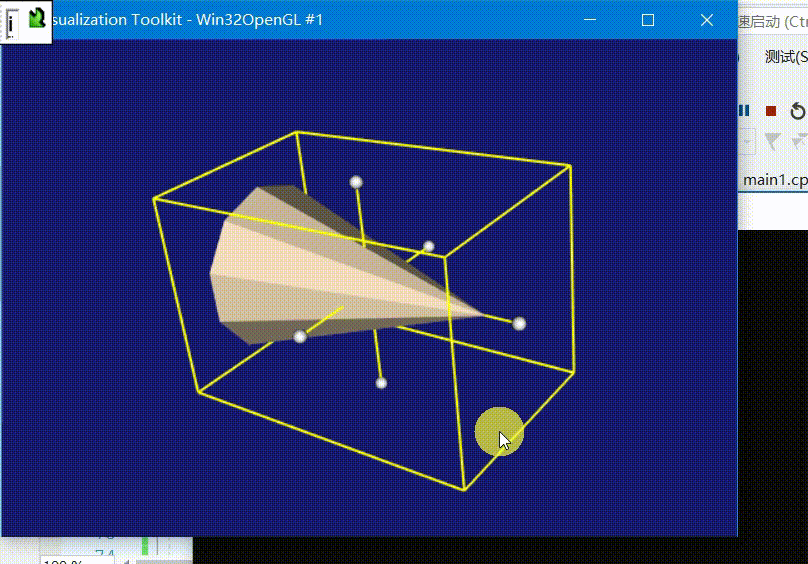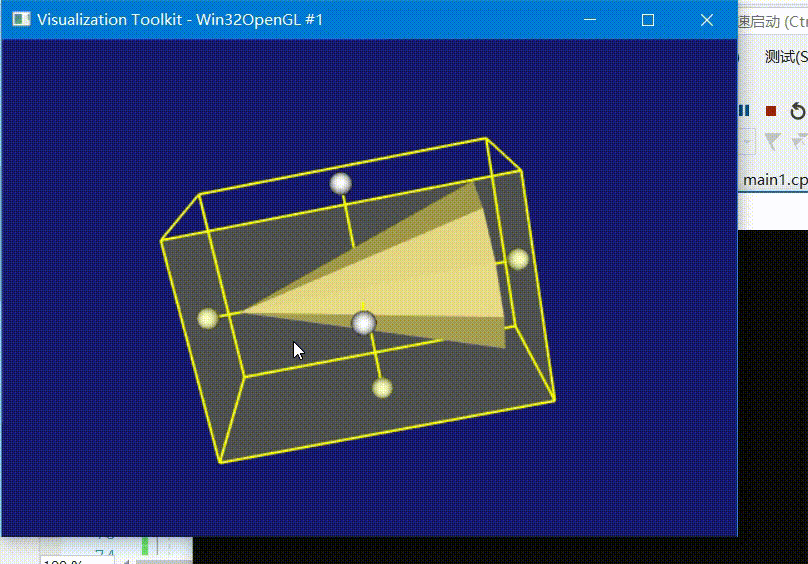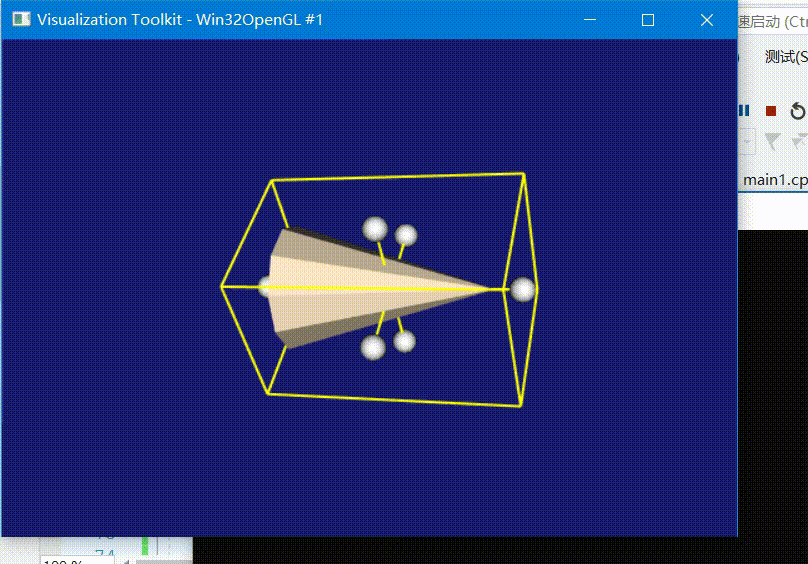
VTK —— 二、教程六 - 为模型加入3D微件(按下i键隐藏或显示)(附完整源码)
代码效果 本代码编译运行均在如下链接文章生成的库执行成功,若无VTK库则请先参考如下链接编译vtk源码: VTK —— 一、Windows10下编译VTK源码,并用Vs2017代码测试(附编译流程、附编译好的库、vtk测试源码) 教程描述 本…...

一种基于图搜索的全局/局部路径避障策略
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言一种基于图搜索的全局/局部路径避障策略前言 认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长! 本文先对一种基于图搜索…...

LT2611UX四端口 LVDS转 HDMI2.0,带音频
描述LT2611UX 是一款面向机顶盒、DVD 应用的高性能 LVDS 至 HDMI2.0 转换器。LVDS输入可配置为单端口、双端口或四端口,具有1个高速时钟通道和3~4个高速数据通道,工作速率最高为1.2Gbps/通道,可支持高达19.2Gbps的总带宽。LT2611UX 支持灵活的…...

TypeError报错处理
哈喽,大家好,我是木头左! 一、Python中的TypeError简介 这个错误通常表示在方法调用时,参数类型不正确,或者在对字符串进行格式化操作时,提供的变量与预期不符。 二、错误的源头:字符串格式化…...
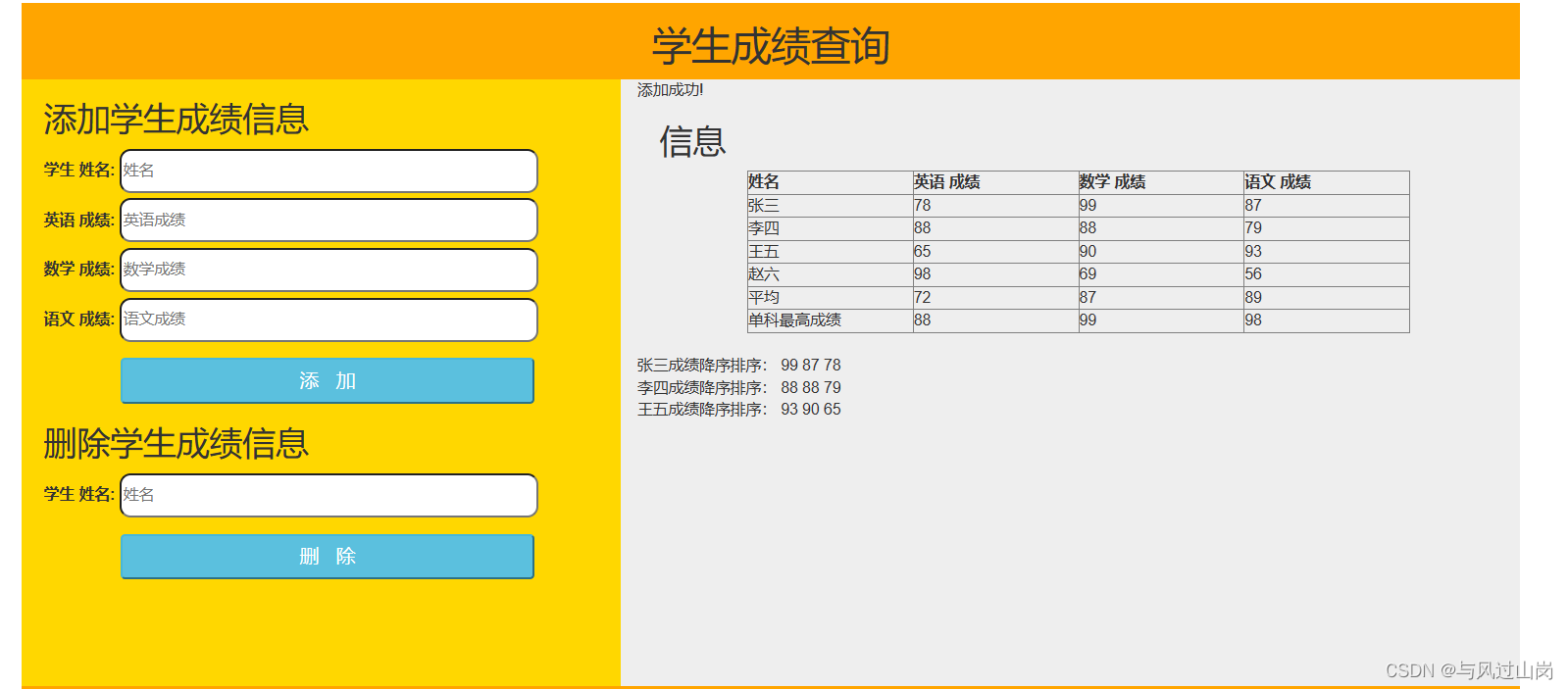
PHP的数组练习实验
实 验 目 的 掌握索引和关联数组,以及下标和元素概念; 掌握数组创建、初始化,以及元素添加、删除、修改操作; 掌握foreach作用、语法、执行过程和使用; 能应用数组输出表格和数据。 任务1:使用一维索引数…...
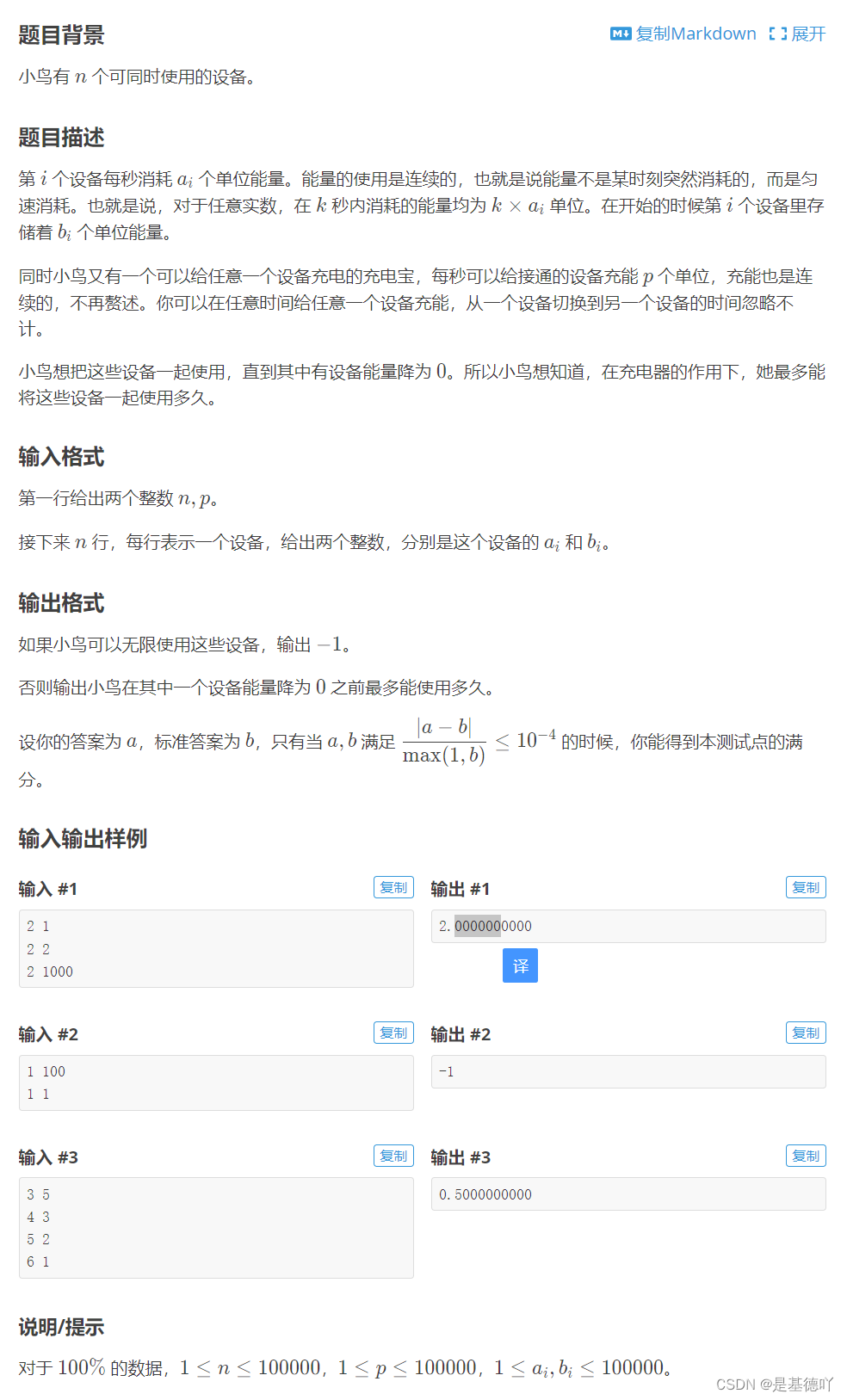
P3743 小鸟的设备
原题链接:小鸟的设备 - 洛谷 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 浮点数二分答案。 首先特判,如果接通设备每秒生成的能量p大于等于所有设备每秒消耗的能量(a[1]a[2]..a[n])直接输出-1&…...

数字旅游以科技创新为动力:推动旅游服务的智能化、网络化和个性化发展,满足游客日益增长的多元化、个性化需求
目录 一、引言 二、科技创新推动旅游服务智能化发展 1、智能化技术的引入与应用 2、智能化提升旅游服务效率与质量 三、科技创新推动旅游服务网络化发展 1、网络化平台的构建与运营 2、网络化拓宽旅游服务渠道与范围 四、科技创新推动旅游服务个性化发展 1、个性化需求…...

64位的IP地址设想
现有的IP地址 IPv4有32位,不够用了。 IPv6有128位,相当多。 实际上,23385亿,只要在IPv4的基础上,加1比特就够用了,IPv6有些太长了。 64位的IP地址 这是个设想。 64位分成七段,8888881664&…...
1.python爬虫爬取视频网站的视频可下载的源url
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、爬取的源网站二、实现代码总结 一、爬取的源网站 http://www.lzizy9.com/ 在这里以电影片栏下的动作片为例来爬取。 可以看到视频有多页,因此需要…...

Linux目录结构
目录结构必背 !!!!(在生产环境中必须知道自己在哪个目录下)...
电脑问题2【彻底删除CompatTelRunner】
彻底删除CompatTelRunner 电脑偶尔会运行CompatTelRunner造成CPU占用的资源非常大,所以这里要想办法彻底关闭他 本文摘录于:https://mwell.tech/archives/539只是做学习备份之用,绝无抄袭之意,有疑惑请联系本人! 解决办法是进入W…...

【算法】【贪心算法】【leetcode】870. 优势洗牌
题目地址:https://leetcode.cn/problems/advantage-shuffle/description/ 题目描述: 给定两个长度相等的数组 nums1 和 nums2,nums1 相对于 nums2 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。 返回 nums1 的任意排列&…...
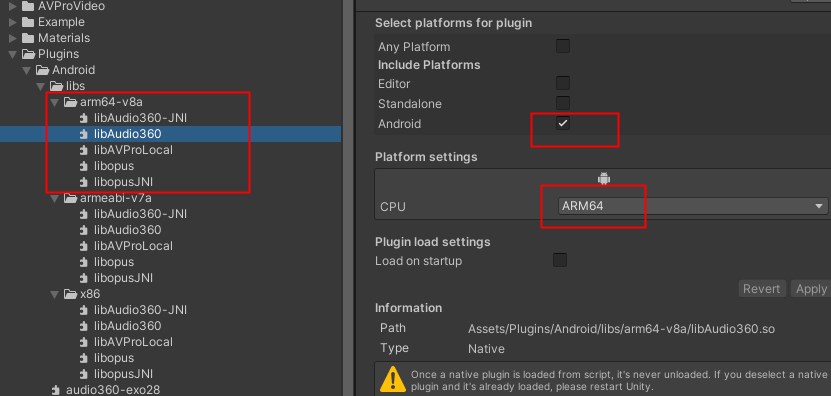
Unity AVProVideo安卓播放视频问题
打包ARM64,插件里arm64里的几个库都设置arm64,平台选择安卓 Unity VideoPlayer使用url方式,Android平台下无法播放http链接的视频 主要原因:默认情况下,不允许从Android 8开始使用不安全的HTTP,并且必须使用HTTPS,除非分配了自定义的明文安全策略 解决办法: 只需要修…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
