为什么要梯度累积
文章目录
- 梯度累积
- 什么是梯度累积
- 如何理解理解梯度累积
- 梯度累积的工作原理
- 梯度累积的数学原理
- 梯度累积过程
- 如何实现梯度累积
- 梯度累积的可视化
梯度累积
什么是梯度累积
随着深度学习模型变得越来越复杂,模型的训练通常需要更多的计算资源,特别是在训练期间需要更多的内存。在训练深度学习模型时,在硬件资源有限的情况下,很难使用大批量数据进行有效学习。大批量数据通常可以带来更好的梯度估计,但同时也需要大量的内存。
梯度累积是一种巧妙的技术,它允许在不增加内存需求的情况下,有效地使用更大的批量数据来训练深度学习模型。
如何理解理解梯度累积
梯度累积本质上涉及将大批量划分为较小的子批量,并在这些子批量上累积计算出的梯度。这一过程模拟了使用较大批量训练的情况。
梯度累积的工作原理
以下是梯度累积过程的逐步分解:
- 分而治之:将你的硬件无法处理的大批量划分为更小的、可管理的子批量。
- 累积梯度:不是在处理每个子批量后更新模型参数,而是在几个子批量上累积梯度。
- 参数更新:在处理了预定义数量的子批量后,使用累积的梯度来更新模型参数。
这种方法使得模型能够利用大批量的稳定性和收敛性,而不必提高内存成本。
梯度累积的数学原理

梯度累积过程
在深度学习模型中,一个完整的前向和反向传播过程如下:
-
前向传播:数据通过神经网络,层层处理后得到预测结果。
-
损失计算:使用损失函数计算预测结果与实际值之间的差异。以平方误差损失函数为例:
L ( θ ) = 1 2 ( h ( x k ) − y k ) 2 L(\theta) = \frac{1}{2} (h(x_k) - y_k)^2 L(θ)=21(h(xk)−yk)2
这里 L ( θ ) L(\theta) L(θ) 表示损失函数, θ \theta θ 代表模型参数, h ( x k ) h(x_k) h(xk) 是对输入 x k x_k xk 的预测输出, y k y_k yk 是对应的真实输出。
-
反向传播:计算损失函数相对于模型参数的梯度(对上式求导):
∇ θ L ( θ ) = ( h ( x k ) − y k ) ⋅ ∇ θ h ( x k ) \nabla_\theta L(\theta) = (h(x_k) - y_k) \cdot \nabla_\theta h(x_k) ∇θL(θ)=(h(xk)−yk)⋅∇θh(xk)
-
梯度累积:在传统的训练过程中,每完成一个批次的数据处理后就会更新模型参数。而在梯度累积中,梯度不是立即用来更新参数,而是累加多个小批次的梯度:
G = ∑ i = 1 n ∇ θ L i ( θ ) G = \sum_{i=1}^{n} \nabla_{\theta} L_i(\theta) G=i=1∑n∇θLi(θ)
这里 G G G 是累积梯度, L i ( θ ) L_i(\theta) Li(θ) 是第 i i i 个batch的损失函数。
-
参数更新:累积足够的梯度后,使用以下公式更新参数:
θ = θ − η ⋅ G \theta = \theta - \eta \cdot G θ=θ−η⋅G
其中 l r lr lr 是学习率,用于控制更新的步长。
如何实现梯度累积
以下是在 PyTorch 中实现梯度累积的示例:
# 模型定义
model = ...
optimizer = ...# 累积步骤数
accumulation_steps = 4for epoch in range(num_epochs):optimizer.zero_grad()for i, (inputs, labels) in enumerate(dataloader):outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()# 只有在处理足够数量的子批量后才更新参数if (i + 1) % accumulation_steps == 0:optimizer.step()optimizer.zero_grad()# 如果批量大小不是累积步数的倍数,确保在每个epoch结束时更新if (i + 1) % accumulation_steps != 0:optimizer.step()optimizer.zero_grad()
这个例子中,accumulation_steps 定义了在参数更新前需要累积的batch数量。
梯度累积的可视化
为了更好地理解梯度累积的影响,可视化可以非常有帮助。以下是一个例子,说明如何在神经网络中可视化梯度流,以监控梯度是如何被累积和应用的:
import matplotlib.pyplot as plt# 绘制梯度流动的函数
def plot_grad_flow(named_parameters):ave_grads = []layers = []for n, p in named_parameters:if (p.requires_grad) and ("bias" not in n):layers.append(n)ave_grads.append(p.grad.abs().mean())plt.plot(ave_grads, alpha=0.3, color="b")plt.hlines(0, 0, len(ave_grads)+1, linewidth=1, color="k")plt.xticks(range(0, len(ave_grads), 1), layers, rotation="vertical")plt.xlim(xmin=0, xmax=len(ave_grads))plt.xlabel("层")plt.ylabel("平均梯度")plt.title("网络中的梯度流")plt.grid(True)plt.show()# 在训练过程中或训练后调用此函数以可视化梯度流
plot_grad_flow(model.named_parameters())
参考资料:
-
Gradient Accumulation Algorithm
-
Performing gradient accumulation with 🤗 Accelerate
-
梯度累加(Gradient Accumulation)
相关文章:

为什么要梯度累积
文章目录 梯度累积什么是梯度累积如何理解理解梯度累积梯度累积的工作原理 梯度累积的数学原理梯度累积过程如何实现梯度累积 梯度累积的可视化 梯度累积 什么是梯度累积 随着深度学习模型变得越来越复杂,模型的训练通常需要更多的计算资源,特别是在训…...
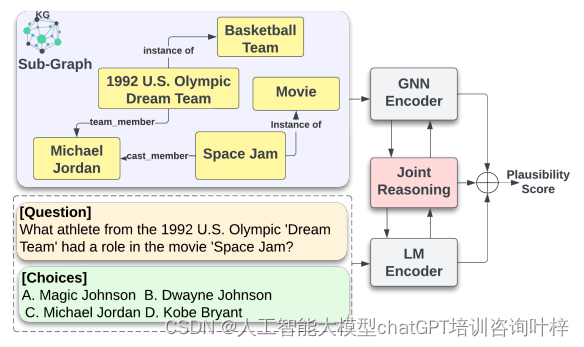
知识图谱在提升大语言模型性能中的应用:减少幻觉与增强推理的综述
幻觉现象指的是模型在生成文本时可能会产生一些听起来合理但实际上并不准确或相关的输出,这主要是由于模型在训练数据中存在知识盲区所致。 为了解决这一问题,研究人员采取了多种策略,其中包括利用知识图谱作为外部信息源。知识图谱通过将信息…...

P8800 [蓝桥杯 2022 国 B] 卡牌
P8800 [蓝桥杯 2022 国 B] 卡牌 分析 “最多” -- 二分 1.二分区间(凑齐的卡牌套数): l:a[]min;r:(a[]b[])max 2.check(x): (1)for循环内: 判断x - a[i…...
)
MySQL商城数据表(80-84)
80商品规格值表 DROP TABLE IF EXISTS niumo_spec_items; CREATE TABLE niumo_spec_items (itemId int(11) NOT NULL AUTO_INCREMENT COMMENT 自增ID,shopId int(11) NOT NULL DEFAULT 0 COMMENT 店铺ID,catId int(11) NOT NULL DEFAULT 0 COMMENT 类型ID,goodsId int(11) NOT…...
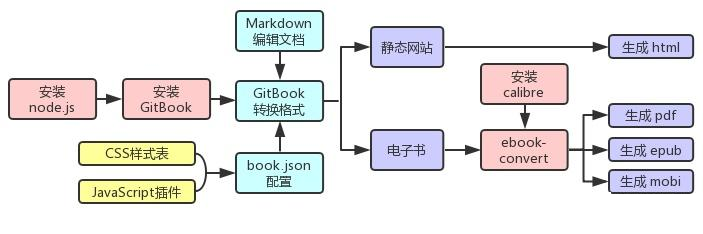
使用Gitbook生成电子书
背景 《Google工程实践文档》相对原文Google’s Engineering Practices documentation ,部分内容过时了。需要更新中文版,并使用Gitbook把Markdown文件转换成对应的PDF电子书。 上一次生成PDF电子书是5年前,当时生成电子书的环境早已不在…...

设计模式之传输对象模式
在编程江湖里,有一种模式,它如同数据的“特快专递”,穿梭于系统间,保证信息的快速准确送达,它就是——传输对象模式(Data Transfer Object, DTO)。这不仅仅是数据的搬运工,更是提升系…...
Re69:读论文 LaMDA: Language Models for Dialog Applications
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文名称:LaMDA: Language Models for Dialog Applications ArXiv网址:https://arxiv.org/abs/2201.08239 本文介绍谷歌提出的对话大模型LaMDA,主要关注对各项指标&#x…...
算法学习:二分查找
🔥 引言 在现代计算机科学与软件工程的实践中,高效数据检索是众多应用程序的核心需求之一。二分查找算法,作为解决有序序列查询问题的高效策略,凭借其对数时间复杂度的优越性能,占据着算法领域里举足轻重的地位。本篇内…...

github提交代码失败解决方案
1.打开github.push 工具 如果未安装github客户端请参考附录github 安装配置 2.设置Git的user name和email git config --global user.name "yourname" git config --global user.email "youremail" 3.生成SSH密钥 查看是否已经有了ssh密钥࿱…...
连锁收银系统总仓到门店库存调拨操作教程
1、进入系统后台,系统后台登录网址: 2、点击商品>门店调拨 3、选择调出仓库和调入门店 4、可选择添加商品逐个进行调拨,也可以批量导入需要调拨的商品 然后点击确定。 5、新增调拨后,系统会显示“待出库”状态 6、仓库已经准备…...
公网tcp转流
之前做过几次公网推流的尝试, 今天试了UDP推到公网, 再用TCP从公网拉下来, 发现不行, 就直接改用TCP转TCP了. 中间中转使用的python脚本, 感谢GPT提供技术支持: import socket import threadingdef tcp_receiver(port, forward_queue):"""接收TCP数据并将其放入…...
【Linux 基础 IO】文件系统
文章目录 1.初步理解文件2. fopen ( )的详解 1.初步理解文件 🐧① 打开文件: 本质是进程打开文件; 🐧②文件没有被打开的时候在哪里呢? ----- 在磁盘中; 🐧③进程可以打开很多个文件吗ÿ…...
Chrome浏览器安装React工具
一、如果网络能访问Google商店,直接安装官方插件即可 二、网络不能访问Google商店,使用安装包进行安装 1、下载react工具包 链接:https://pan.baidu.com/s/1qAeqxSafOiNV4CG3FVVtTQ 提取码:vgwj 2、chrome浏览器安装react工具…...

React常用组件分享
1、轮播组件: React Awesome Slider React Slider Carousel Component - react-awesome-slider...
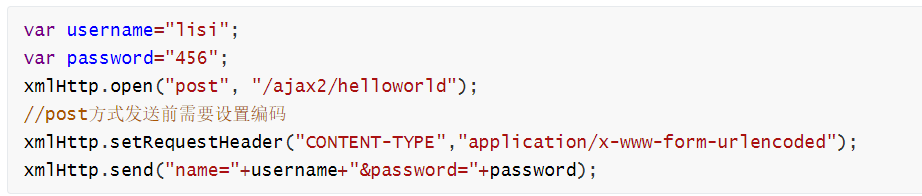
JSON原生AJAX
文章目录 JSONFastjsonfastjson引入fastjson 常用APIfastjson作用常用API使用实例 ajax和json综合(重要)请求参数和响应数据都是普通字符串响应数据改为json格式请求和响应都是js数据封装到Result类和抽取到BaseController 原生AjaxAJAX的执行流程XMLHttpRequest对象使用原生的…...

Go图片列表
需求 在一个页面浏览目录下所有图片 代码 package mainimport ("net/http""fmt""io/ioutil""sort""strings""strconv""net/url" )func handleRequest(w http.ResponseWriter, r *http.Request) { de…...

1.4 初探JdbcTemplate操作
实战目的 掌握Spring框架中JdbcTemplate的使用,实现对数据库的基本操作。理解数据库连接池的工作原理及其在实际开发中的重要性。通过实际操作,加深对Spring框架中ORM(对象关系映射)的理解。 关键技术点 JdbcTemplate操作&…...
React 第二十一章 Portals
Portals 被翻译成传送门,是 React 库中的一个特性,它允许开发者将子组件渲染到父组件 DOM 层次结构之外的其他地方。 React 组件通常是在其父组件的 DOM 层次结构中渲染的,这意味着它们的输出会被插入到父组件的某个 DOM 元素中。然而&#…...

ADS基础教程9-理想模型和厂商模型实现及对比
目录 一、概要二、厂商库使用1.新建cell2.调用厂商库中元器件3.元器件替换及参数选择4.完成参数选择5.导入子图 三、仿真实现注意事项 一、概要 本文将介绍在ADS中调用厂商提供的库,来进行原理图仿真,并实现与ADS系统提供的理想元器件之间的比较。 二、…...
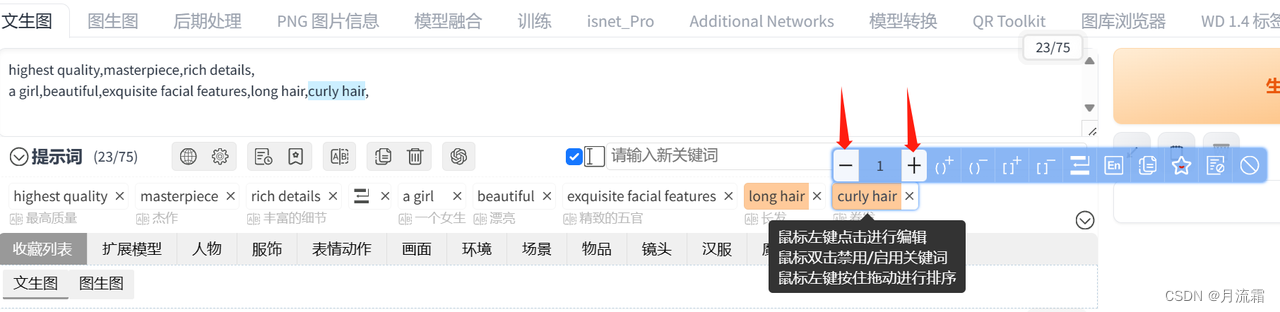
从零开始学AI绘画,万字Stable Diffusion终极教程(二)
【第2期】关键词 欢迎来到SD的终极教程,这是我们的第二节课 这套课程分为六节课,会系统性的介绍sd的全部功能,让你打下坚实牢靠的基础 1.SD入门 2.关键词 3.Lora模型 4.图生图 5.controlnet 6.知识补充 在第一节课里面,我们…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
