前端递归常见应用
概览
在 JavaScript 中,递归是一种编程技术,指的是函数直接或间接调用自身的过程。
递归通常用于解决可以分解为相同子问题的问题。通过不断地将问题分解成更小的、相似的子问题,直到达到某种基本情况(不再需要进一步递归的简单情况)。
递归一般要满足以下两个关键条件:
- 存在基本情况(终止条件):必须有某种简单的情况,在这种情况下递归不再继续进行,避免无限递归导致程序崩溃。
- 能够不断将问题规模缩小:通过递归调用自身,要能逐步将问题转化为更小的、相似的子问题,直到最终达到基本情况。
一. 常见应用
- 递归计算阶乘
function factorial(n) {if (n === 0 || n === 1) {return 1;} else {return n * factorial(n - 1);}
}
当递归终止后,从内到外依次执行。
- 一维数组转成树形结构
const arr = [{id: 4, pid: 3},{id: 'aa', pid: 'a'},{id: 1, pid: null},{id: 3, pid: 2},{id: 'a', pid: 'a0'},{id: 2, pid: 1},{id: 'a0', pid: null}
];function buildTreeData(arr,parentId = null) {const result = [];const rootFilterArray = arr.filter(item => item.pid === parentId);debugger;if(rootFilterArray.length > 0 ) {rootFilterArray.forEach(subitem => {debugger;const children = buildTreeData(arr,subitem.id);if(children.length > 0 ) {subitem.children = children}result.push(subitem)});}return result
}const resData = buildTreeData(arr);
console.log(resData,'resData')
- 查找树形结构子项
const checkTestData = [{"id": 1,"pid": null,"children": [{"id": 2,"pid": 1,"children": [{"id": 3,"pid": 2,"children": [{"id": 4,"pid": 3,"children": []}]}]}]},{"id": "a0","pid": null,"children": [{"id": "a","pid": "a0","children": [{"id": "aa","pid": "a","children": []}]}]}
]function getItemById(arr,id) {for(let item of arr) {debugger;if(item.id === id) {return item} else if(item.children) {const data = getItemById(item.children,id);if(data) {return data}}}
}const resDataItem = getItemById(checkTestData,3);
console.log(resDataItem,'resDataItem')
二. 总结
关键点梳理:
- 递归终止条件确定: 即没有调用自身的函数。
- 递归终止后结果的获取:有的时候直接返回最终的递归结果,有的时候拿到每次递归的结果之后由内至外依次进行逻辑处理。
相关文章:

前端递归常见应用
概览 在 JavaScript 中,递归是一种编程技术,指的是函数直接或间接调用自身的过程。 递归通常用于解决可以分解为相同子问题的问题。通过不断地将问题分解成更小的、相似的子问题,直到达到某种基本情况(不再需要进一步递归的简单情…...

AI工具如何改变我们的工作与生活
AI工具在当今社会中扮演着越来越重要的角色,它们已经开始改变着我们的工作方式和生活方式。在接下来的2000字篇幅中,我将详细探讨AI工具如何影响我们的工作和生活。 AI工具在工作中的影响: 自动化和智能化生产流程: AI工具可以通…...
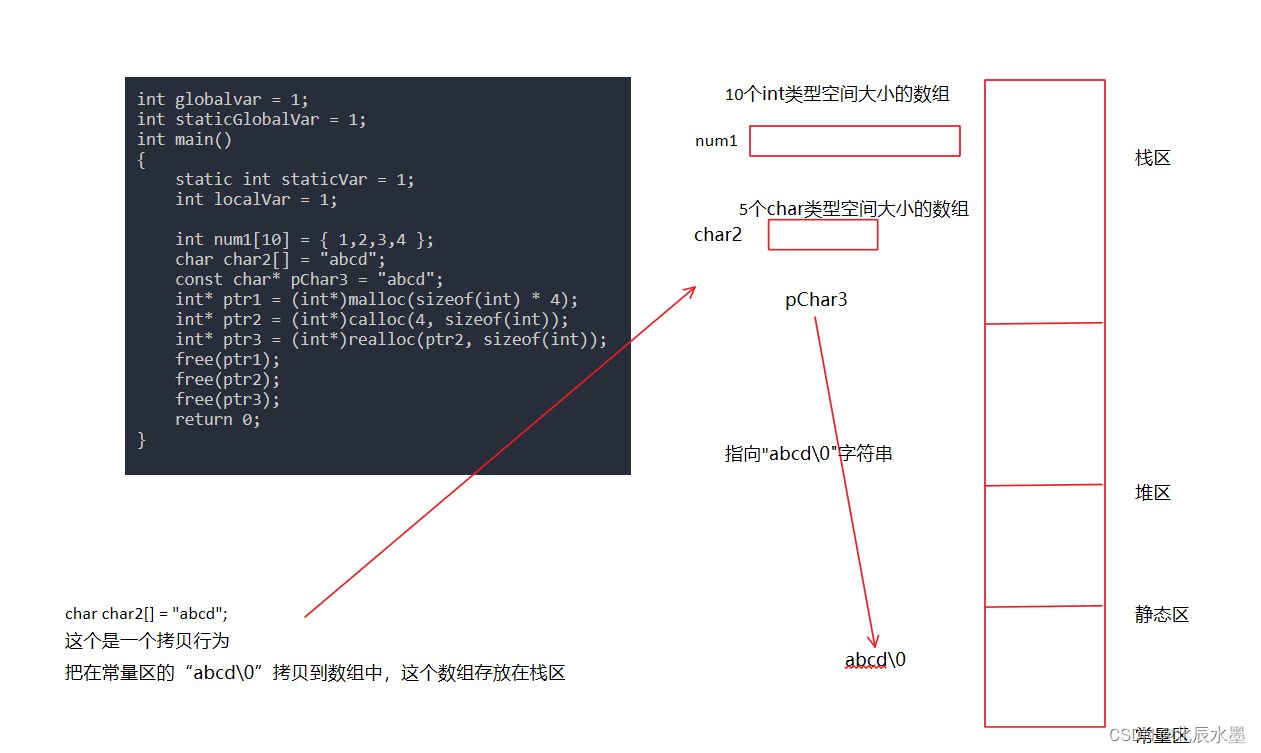
深入了解C/C++的内存区域划分
🔥个人主页:北辰水墨 🔥专栏:C学习仓 本节我们来讲解C/C的内存区域划分,文末会附加一道题目来检验成果(有参考答案) 一、大体有哪些区域?分别存放什么变量开辟的空间? …...

C++构造函数和析构函数的调用顺序
一般情况下,调用析构函数的次序正好与调用构造函数的次序相反,也就是最先被调用的构造函数,其对应的析构函数最后被调用,而最后被调用的构造函数,其对应的析构函数最先被调用。 当然对象的构造函数和析构函数调用时机和…...
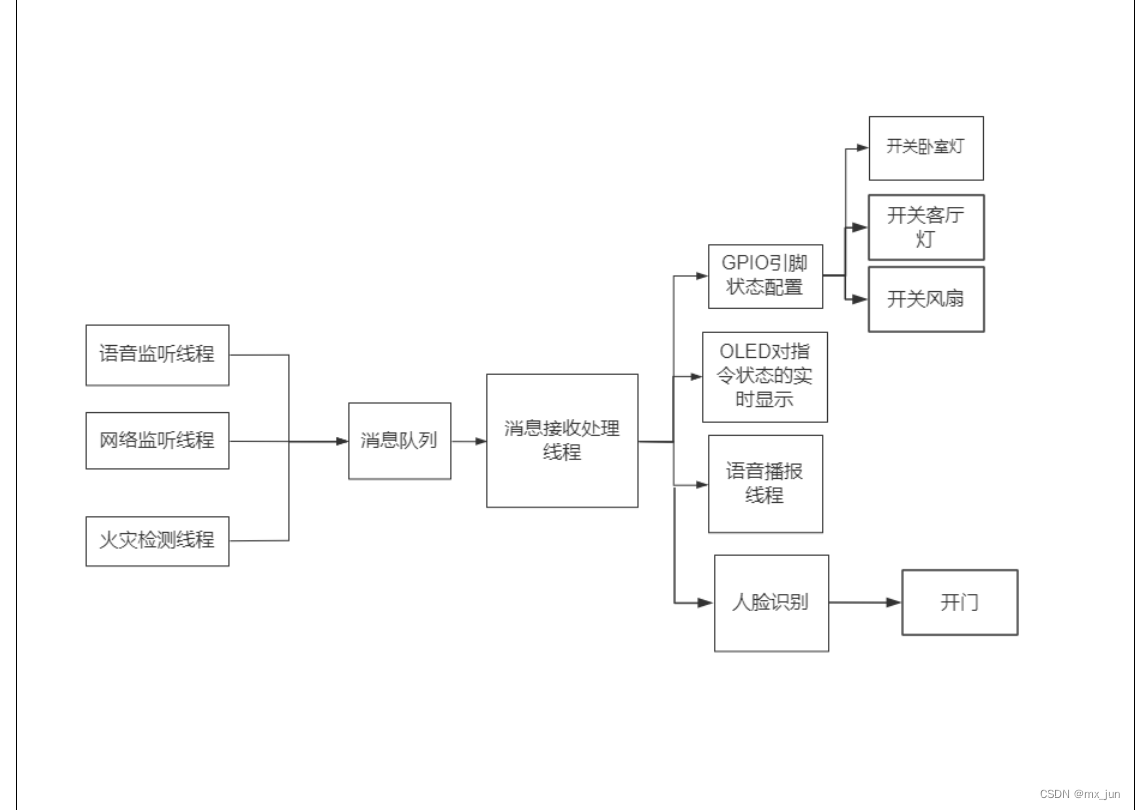
智能家居1 -- 实现语音模块
项目整体框架: 监听线程4: 1. 语音监听线程:用于监听语音指令, 当有语音指令过来后, 通过消息队列的方式给消息处理线程发送指令 2. 网络监听线程:用于监听网络指令,当有网络指令过来后, 通过消息队列的方…...

Leetcode 3139. Minimum Cost to Equalize Array
Leetcode 3139. Minimum Cost to Equalize Array 1. 解题思路2. 代码实现 题目链接:3139. Minimum Cost to Equalize Array 1. 解题思路 这一题是一道hard的题目,而且看了一下答出率低的离谱,就一开始被吓到了,不过实际做了一下…...

【element-ui】el-table横向滚动后,通过is-scrolling-left获取滚动高度失效的问题
el-table横向滚动后,通过is-scrolling-left获取滚动高度失效的问题 需求 现在有一个需求,需要监听el-table的纵向滚动,当滚动高度达到特定值时进行一些操作。 代码如下: methods:{throttledHandleScroll() {// 如果已经有定时器…...

JAVA中的日期
获取当前的日期 LocalDate LocalDate today LocalDate.now();System.out.println("今天是:"today);//今天是:2024-05-06String format today.format(DateTimeFormatter.ofPattern("yyyy年MM月dd日"));System.out.println("今天是:"…...

一起了解开源自定义表单的优势表现
随着社会的进步和科技的发展,越来越多的中小企业希望采用更为先进的软件平台,助力企业实现高效率的流程化管理。低代码技术平台、开源自定义表单已经慢慢走入大众视野,成为一款灵活、高效的数字化转型工具。流辰信息专注于低代码技术平台的研…...

体育老师工资高吗,奖金有吗
教师的薪资水平与多种因素相关,包括教育经验、工作地点、学校类型以及个人的教学成果等。在讨论体育教师的工资问题时,不能仅仅关注数字,更应了解教育价值和个人发展。 初中体育教师的工资水平受多种因素影响。根据网络统计的数据,…...

Linux驱动开发——(十一)INPUT子系统
目录 一、input子系统简介 二、input驱动API 2.1 input字符设备 2.2 input_dev结构体 2.3 上报输入事件 2.4 input_event结构体 三、代码 3.1 驱动代码 3.2 测试代码 四、平台测试 一、input子系统简介 input子系统是管理输入的子系统,和pinctrl、gpio子…...
大数据毕业设计Python+Django旅游景点评论数据采集分析可视化系统 NLP情感分析 LDA主题分析 bayes分类 旅游爬虫 旅游景点评论爬虫 机器学习 深度学习 人工智能 计算机毕业设计
毕业论文(设计)开题报告 学生姓名 学 号 所在学院 信息工程学院 专 业 指导教师姓名 指导教师职称 工程师 助教 指导教师单位 论文(设计)题目 基于朴素贝叶斯算法旅游景点线上评价情感分析 开 题 报 告…...
FSNotes for Mac v6.7.1中文激活版:强大的笔记管理工具
FSNotes for Mac是一款功能强大的文本处理与笔记管理工具,为Mac用户提供了一个直观、高效的笔记记录和整理平台。 FSNotes for Mac v6.7.1中文激活版下载 FSNotes支持Markdown语法,使用户能够轻松设置笔记格式并添加链接、图像等元素,实现笔记…...

课程34:Windows Docker部署.Net Core项目
这里写目录标题 🚀前言一、安装Docker Desktop1.1 官网下载Docker1.2 安装Docker1.2.1 选择配置,默认都勾选1.2.2 安装中1.2.3 安装成功1.2.4 启动1.2.5 启动成功二、.Net Core 项目发布与部署2.1 修改Dockerfile文件2.2 Web项目发布2.3 修改配置2.3.1 修改dockerfile<...
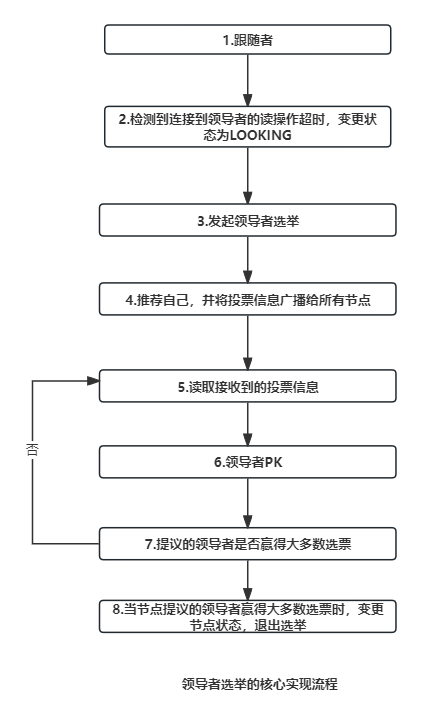
分布式与一致性协议之ZAB协议(四)
ZAB协议 ZooKeeper是如何选举领导者的。 首先我们来看看ZooKeeper是如何实现成员身份的? 在ZooKeeper中,成员状态是在QuorumPeer.java中实现的,为枚举型变量 public enum ServerState { LOOKING, FOLLOWING, LEADING, OBSERVING }其实&…...
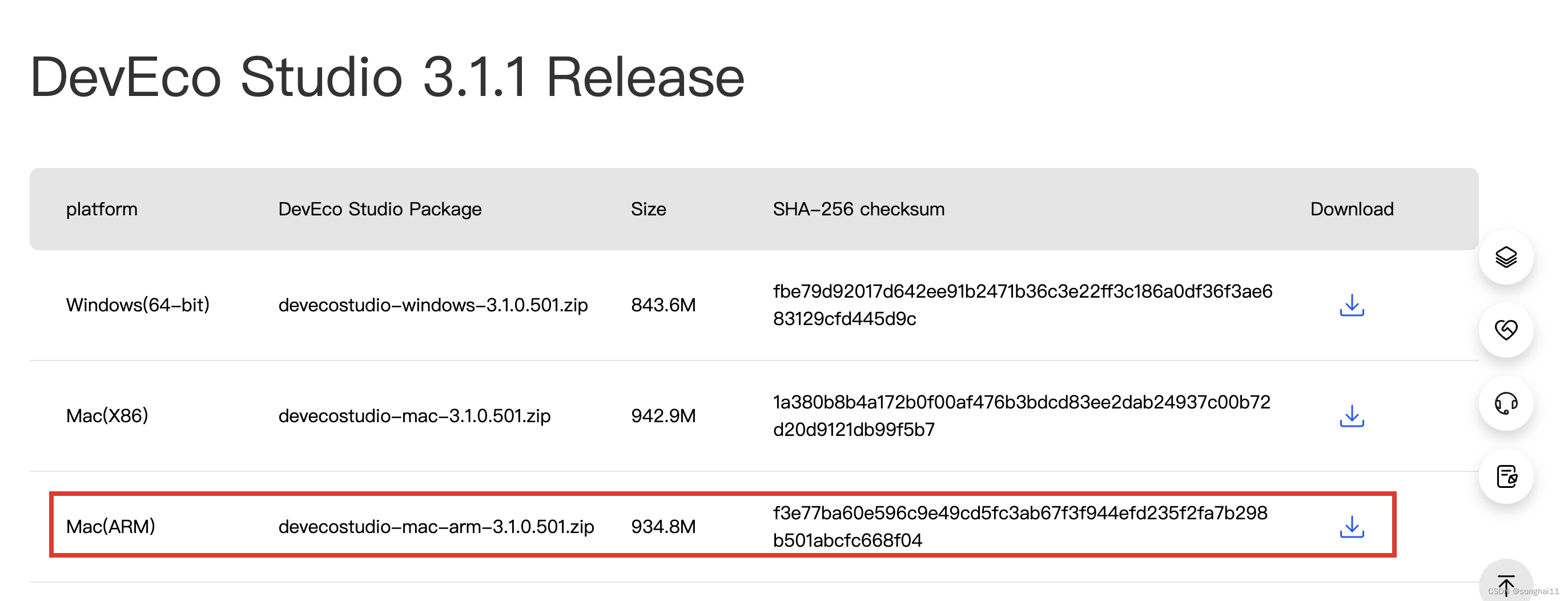
在M1芯片安装鸿蒙闪退解决方法
在M1芯片安装鸿蒙闪退解决方法 前言下载鸿蒙系统安装完成后,在M1 Macos14上打开闪退解决办法接下来就是按照提示一步一步安装。 前言 重新安装macos系统后,再次下载鸿蒙开发软件,竟然发现打不开。 下载鸿蒙系统 下载地址:http…...
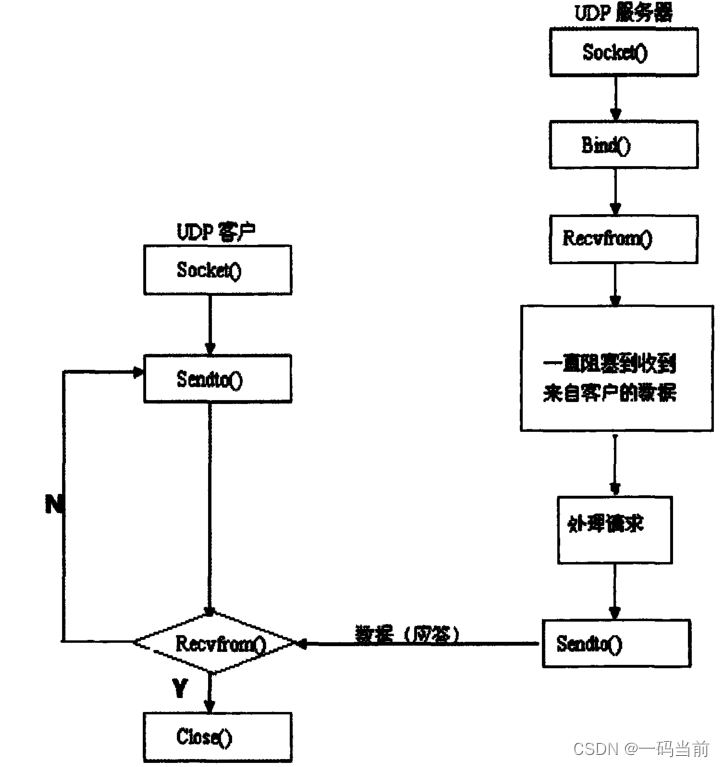
Linux基础-socket详解、TCP/UDP
文章目录 一、Socket 介绍二、Socket 通信模型三、Socket 常用函数1 创建套接字2 绑定套接字3、监听连接4、接受连接5、接收和发送数据接收数据发送数据 6、关闭套接字 四、Socket编程试验1、源码server.cclient.c 2、编译:3、执行结果 五、补充TCP和UDP协议的Socke…...

【菜单下拉效果】基于jquery实现二级菜单下拉效果(附完整源码下载)
Js菜单下拉特效目录 🍔涉及知识🥤写在前面实现效果🍧一、涉及知识🌳二、具体实现2.1 搭建一级菜单2.2 搭建二级菜单项2.3 引入js文件2.4 构建CSS文件 🐋三、源码获取🌅 作者寄语 🍔涉及知识 ht…...

如何使用resource-counter统计跨Amazon区域的不同类型资源数量
关于resource-counter resource-counter是一款功能强大的命令行工具,该工具基于纯Python 3开发,可以帮助广大研究人员跨Amazon区域统计不同类型资源的数量。 该工具在统计完不同区域的各类资源数量后,可以在命令行中输出并显示统计结果。res…...

nextTick的作用与原理
在 Vue 中,nextTick允许我们延迟执行一段代码,直到 Vue完成其当前的 DOM 更新周期。这使得我们可以在 DOM 更新后安全地访问和修改 DOM 元素。 一、Vue 的异步更新策略 Vue 采用了一种称为异步更新策略的机制。这意味着当数据发生变化时,Vue…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
