数据结构===堆
文章目录
- 概要
- 堆
- 2条件
- 大顶堆
- 小顶堆
- 堆的实现
- 插入元素
- 删除堆顶元素
- 堆代码
- 小结
概要
堆,有趣的数据结构。
那么,如何实现一个堆呢?
堆
堆,有哪些重点:
- 满足2条件
- 大顶堆
- 小顶堆
2条件
2条件:
- 堆是一个完全二叉树
- 堆中的每个节点的值都必须大于等于或小于等于其树中每个节点的值
堆要满足这2个条件,重点。即使后边插入数据,或者删除数据之后,还是要满足这2个条件来做调整。
大顶堆
特点:
每个节点的值都大于等于子树中每个节点值的堆。
小顶堆
特点:
每个节点的值都小于等于子树中每个节点值的堆。
堆的实现
实现一个堆,重要的操作:插入元素和删除堆顶元素
插入元素
堆化:顺着节点所在的路径,向上或者向下,对比,然后交换。
来看下插入的代码:
public class Heap {private int[] a; // 数组,从下标1开始存储数据private int n; // 堆可以存储的最大数据个数private int count; // 堆中已经存储的数据个数public Heap(int capacity) {a = new int[capacity + 1];n = capacity;count = 0;}public void insert(int data) {if (count >= n) return; // 堆满了++count;a[count] = data;int i = count;while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化swap(a, i, i/2); i = i/2;}}}
删除堆顶元素
由大顶堆和小顶堆的定义可知,堆顶元素要么最大,要么最小;
public void removeMax() {if (count == 0) return -1; // 堆中没有数据a[1] = a[count];--count;heapify(a, count, 1);
}private void heapify(int[] a, int n, int i) { // 自上往下堆化while (true) {int maxPos = i;if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;if (maxPos == i) break;swap(a, i, maxPos);i = maxPos;}
}
堆代码
来看个完整的代码吧,这里给python的。如下:
import sys
class BinaryHeap:def __init__(self, capacity):self.capacity = capacityself.size = 0self.Heap = [0]*(self.capacity + 1)self.Heap[0] = -1 * sys.maxsizeself.FRONT = 1def parent(self, pos):return pos//2def leftChild(self, pos):return 2 * pos def rightChild(self, pos):return (2 * pos) + 1def isLeaf(self, pos):if pos >= (self.size//2) and pos <= self.size:return Truereturn Falsedef swap(self, fpos, spos):self.Heap[fpos], self.Heap[spos] = self.Heap[spos], self.Heap[fpos]def heapifyDown(self, pos):if not self.isLeaf(pos):if (self.Heap[pos] > self.Heap[self.leftChild(pos)] or self.Heap[pos] > self.Heap[self.rightChild(pos)]):if self.Heap[self.leftChild(pos)] < self.Heap[self.rightChild(pos)]:self.swap(pos, self.leftChild(pos))self.heapifyDown(self.leftChild(pos))else:self.swap(pos, self.rightChild(pos))self.heapifyDown(self.rightChild(pos))def insert(self, element):if self.size >= self.capacity :returnself.size+= 1self.Heap[self.size] = elementcurrent = self.sizewhile self.Heap[current] < self.Heap[self.parent(current)]:self.swap(current, self.parent(current))current = self.parent(current)def minHeap(self):for pos in range(self.size//2, 0, -1):self.heapifyDown(pos)def delete(self):popped = self.Heap[self.FRONT]self.Heap[self.FRONT] = self.Heap[self.size]self.size-= 1self.heapifyDown(self.FRONT)return poppeddef isEmpty(self):return self.size == 0def isFull(self):return self.size == self.capacity
小结
关于堆,就这么多吧
堆的概念跟推理还是相对来说简单的。比红黑树简单点。其实都一样的,只要按照那些规则,一条一条对着去理解;应该还好。
相关文章:

数据结构===堆
文章目录 概要堆2条件大顶堆小顶堆 堆的实现插入元素删除堆顶元素 堆代码小结 概要 堆,有趣的数据结构。 那么,如何实现一个堆呢? 堆 堆,有哪些重点: 满足2条件大顶堆小顶堆 2条件 2条件: 堆是一个…...
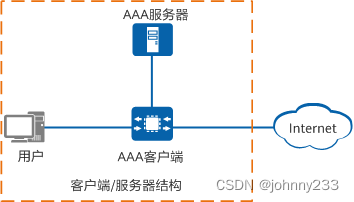
AAA、RADIUS、TACACS、Diameter协议介绍
准备软考高级时碰到的一个概念,于是搜集网络资源整理得出此文。 概述 AAA是Authentication、Authorization、Accounting的缩写简称,即认证、授权、记帐。Cisco开发的一个提供网络安全的系统。AAA协议决定哪些用户能够访问服务,以及用户能够…...
)
Nacos高频面试题及参考答案(2万字长文)
目录 Nacos是什么?它的主要功能有哪些? Nacos在微服务架构中扮演什么角色?...

CMakeLists.txt语法规则:条件判断中表达式说明四
一. 简介 前面学习了 CMakeLists.txt语法中的 部分常用命令,常量变量,双引号的使用。 前面几篇文章也简单了解了 CMakeLists.txt语法中的条件判断,文章如下: CMakeLists.txt语法规则:条件判断说明一-CSDN博客 CMa…...
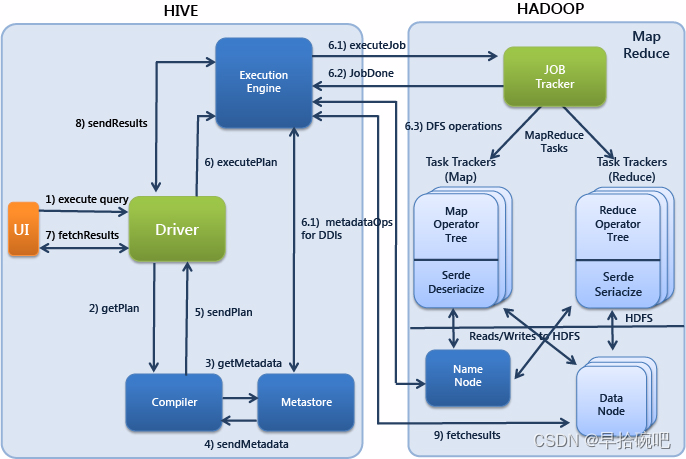
Hive概述
Hive简介 Hive是一个基于Hadoop的开源数据仓库工具,用于存储和处理海量结构化数据. 它是Facebook在2008年8月开源的一个数据仓库框架,提供了类似于SQL语法的HQL(HiveSQL)语句作为数据访问接口. Hive可以做复查统计分析之类的工作; 利用hdfs的存储空间,进行结构化数据的存储; 利…...
buuctf-misc-33.[BJDCTF2020]藏藏藏1
33.[BJDCTF2020]藏藏藏1 题目:藏了很多层,一层一层的剥开 常规思路,先使用010打开一下看看 binwalk不行用foremost 发现是pk文件也就是压缩包,并且包含了docx文件 这不binwalk分离一下文件?虽然可以看出有隐藏文件&…...

golang 基础知识细节回顾
之前学习golang的速度过于快,部分内容有点囫囵吞枣的感觉,写gorm过程中有很多违反我常识的地方,我通过复习去修正了我之前认知错误和遗漏的地方。 itoa itoa自增的作用在编辑error code时候作用很大,之前编辑springboot的error c…...

递归陷阱七例
目录 栈溢出 无限递归 大常数参数 递归深度过大 重复计算 函数调用开销 递归与迭代的选择 总结 递归是一种强大的编程技术,它允许函数调用自身。递归在很多情况下可以简化代码,使问题更容易理解和解决。然而,递归也容易导致一些常见的…...
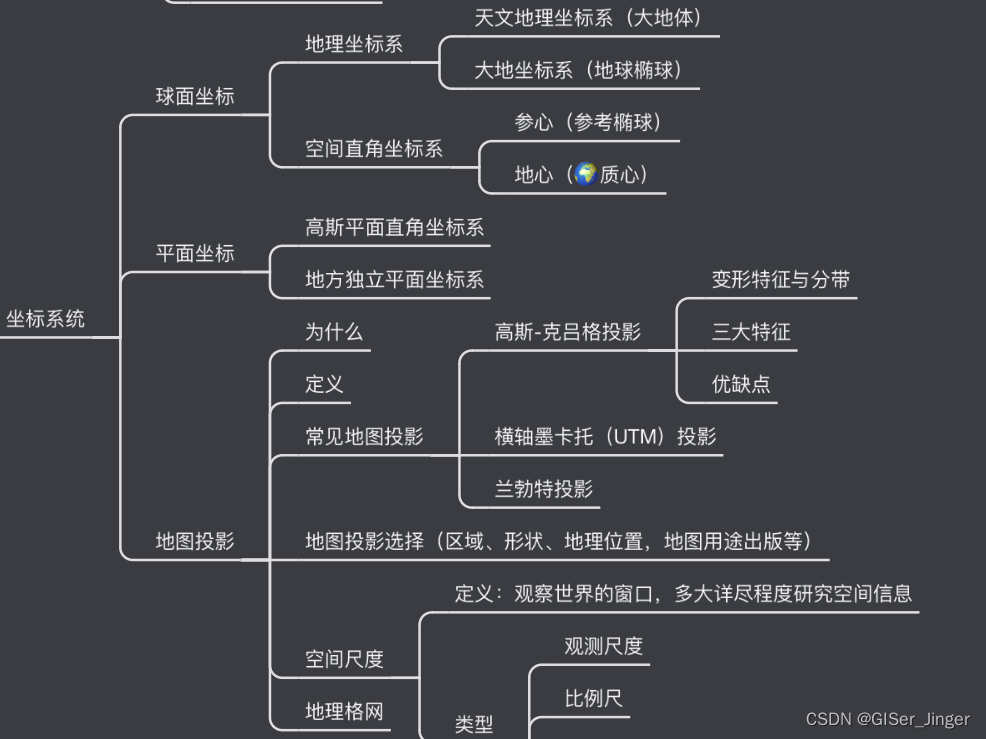
【3D基础】坐标转换——地理坐标投影到平面
汤国安版GIS原理第二章重点 1.常见投影方式 https://download.csdn.net/blog/column/9283203/83387473 Web Mercator投影(Web Mercator Projection): 优点: 在 Web 地图中广泛使用,易于显示并与在线地图服务集成。在…...

颈椎锻炼方式
1. 颈部伸展运动:坐直,慢慢将头向前伸展,直到感到轻微的拉伸,保持数秒钟,然后缓慢放松。重复10次。 2. 颈部旋转运动:坐直,慢慢将头向一侧转动,直到感到轻微的拉伸,保持…...
测试环境搭建:JDK+Tomcat+Mysql+Redis
基础的测试环境搭建: LAMPLinux(CentOS、ubuntu、redhat)ApacheMysqlPHP LTMJLinux(CentOS、ubuntu、redhat)TomcatMysql(Oracle)RedisJava 真实的测试环境搭建:(企业真实的运维) 基于SpringBoot(SpringCloud分布式微…...
 Object Pascal 学习笔记---第11章第1节(混合引用中的错误))
(delphi11最新学习资料) Object Pascal 学习笔记---第11章第1节(混合引用中的错误)
11.1.3 混合引用中的错误 在使用对象时,你通常应该只使用对象变量或接口变量来访问它们。混合使用这两种方法会破坏对象 Pascal 所提供的引用计数机制,并可能导致极难跟踪的内存错误。在实践中,如果你决定使用接口,你可能应该…...
代码随想录算法训练营第三天 | 链表理论基础,203.移除链表元素,707.设计链表,206.反转链表
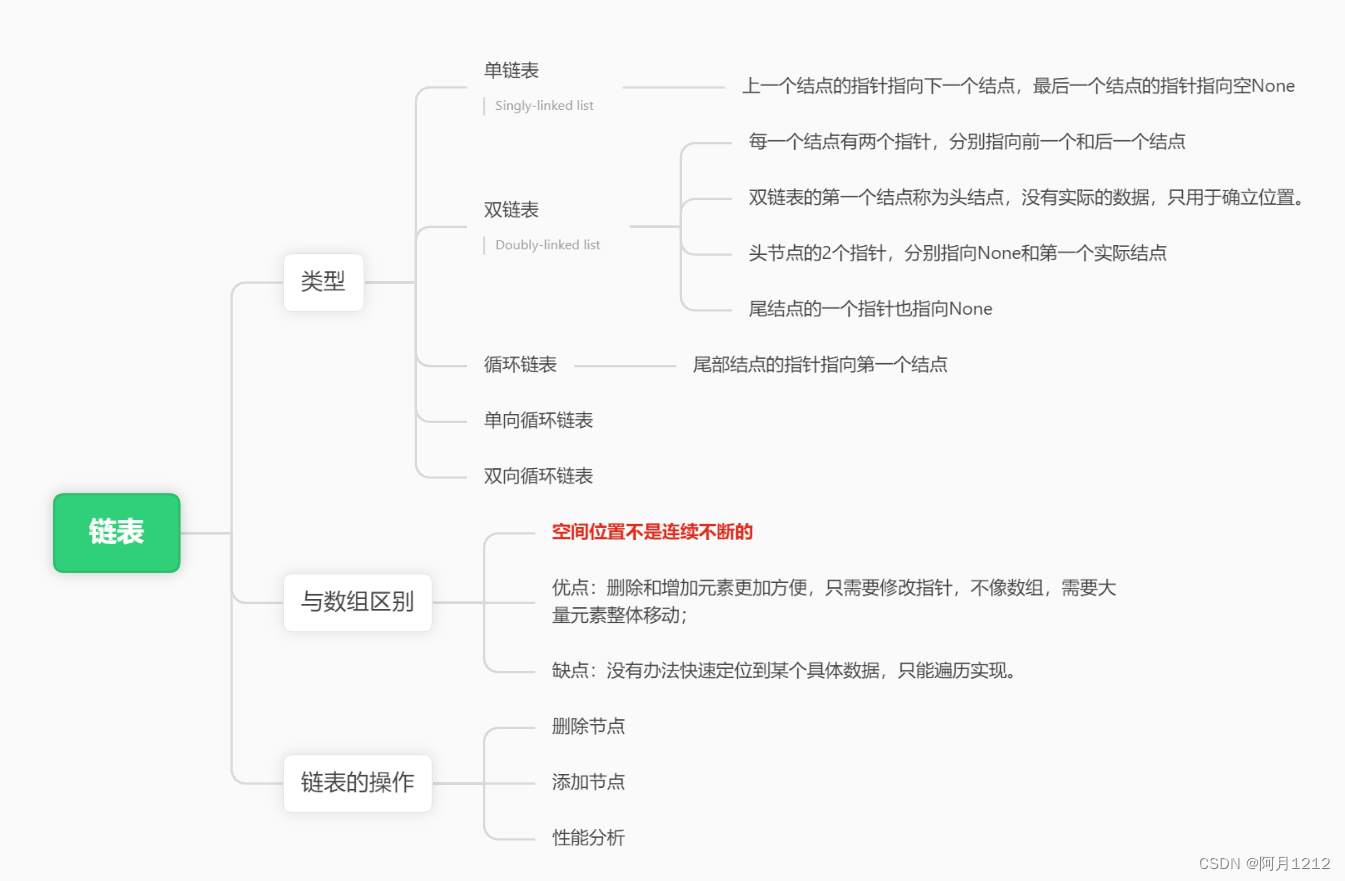
对于链表完全陌生,但是看题目又觉得和数组一样的 链表理论基础 Q:什么是链表? A:链表是由一系列结点组成的。每一个结点由两部分组成:数据和指针。 203.移除链表元素 题目: 给你一个链表的头节点 head 和…...

如何利用仪表构造InfiniBand流量在数据中心测试中的应用
一、什么是Infiniband? 在当今数据爆炸的时代,数据中心作为信息处理的中心枢纽,面临着前所未有的挑战。传统的通信方式已经难以满足日益增长的数据传输需求,而InfiniBand技术的出现,为数据中心带来了全新的通信解决方…...

Kubernetes 文档 / 概念 / Kubernetes 架构 / 节点
Kubernetes 文档 / 概念 / Kubernetes 架构 / 节点 此文档从 Kubernetes 官网摘录 中文地址 英文地址 节点上的组件包括 kubelet、 容器运行时以及 kube-proxy。 管理 向 API 服务器添加节点的方式主要有两种: 节点上的 kubelet 向控制面执行自注册;…...

ICode国际青少年编程竞赛- Python-1级训练场-for循环练习
ICode国际青少年编程竞赛- Python-1级训练场-for循环练习 1、 for i in range(3):Dev.step(4)Dev.turnLeft()2、 for i in range(3):Dev.step(2)Dev.turnRight()Dev.step(2)Dev.turnLeft()3、 for i in range(3):Dev.step(2)Dev.turnRight()Dev.step(2)Dev.turnLeft()4、 for…...
Flutter分模块开发、模块可单独启动、包含Provider
前言 当前案例 Flutter SDK版本:3.13.2 目前Flutter都是在一个项目中,创建不同目录进行模块开发,我进行Android原生开发时,发现原生端,是可以将每个模块独立运行起来的,灵感来自这; 折腾了几…...

Element-UI快速入门:构建优雅的Vue.js应用界面
Element-UI是一套基于Vue.js的组件库,提供了丰富的UI组件和交互效果,帮助开发者快速构建出美观、功能丰富的Web应用界面。本文将介绍如何快速入门Element-UI,并搭建一个简单的示例界面。 步骤一:安装Element-UI 首先,…...

Flutter 中的 @immutable:深入解析与最佳实践
在 Flutter 开发中,immutable 注释扮演着至关重要的角色,用于标记不可变类。不可变类顾名思义,其状态一旦创建便不可更改,这与可变类截然不同。后者允许在创建后对实例进行修改。 immutable 的利好 引入不可变类可以带来诸多优势…...
Pandas数据可视化 - Matplotlib、Seaborn、Pandas Plot、Plotly
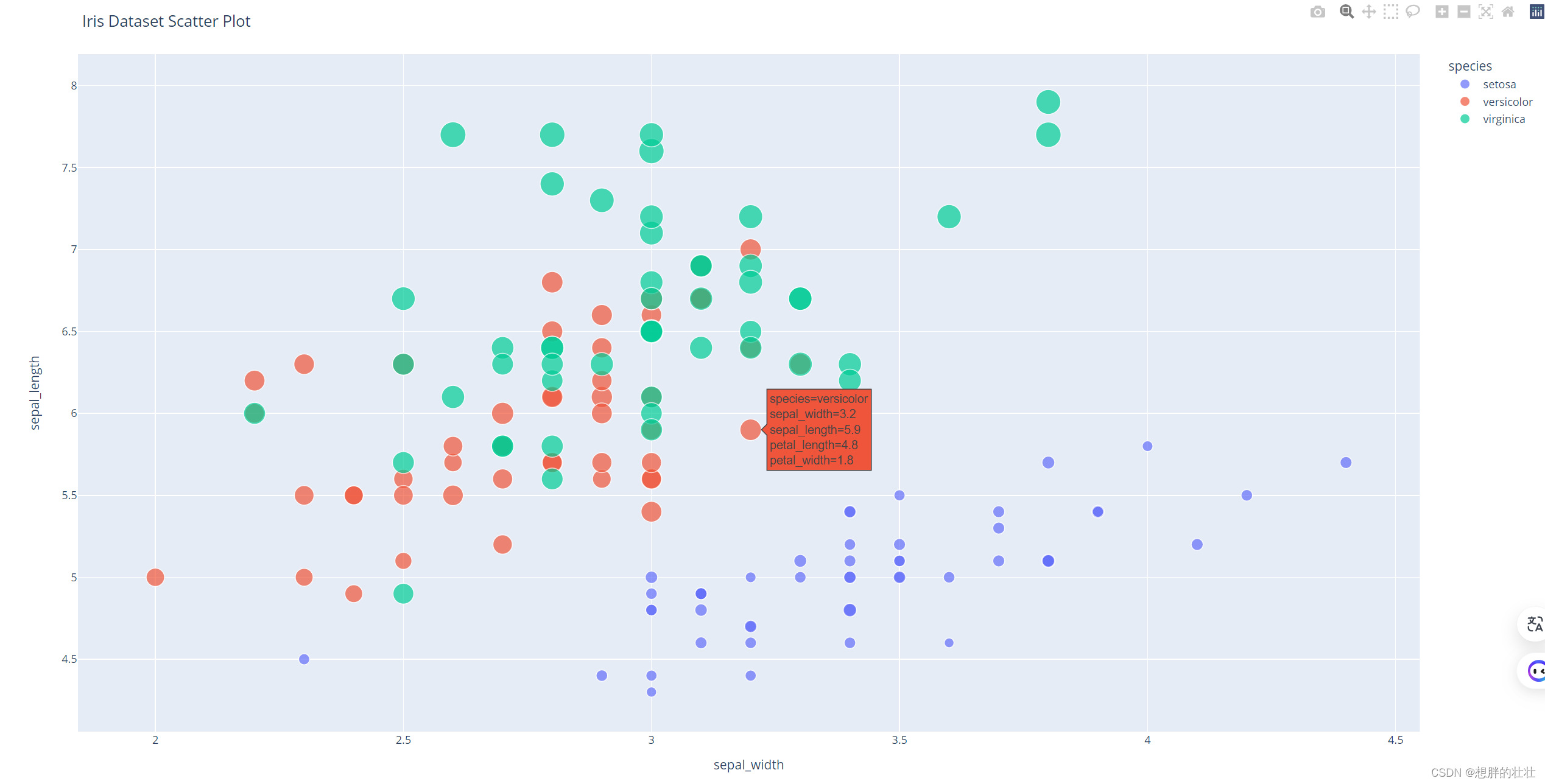
可视化工具介绍 让我们一起探讨Matplotlib、Seaborn、Pandas Plot和Plotly这四个数据可视化库的优缺点以及各自的适用场景。这有助于你根据不同的需求选择合适的工具。 1. Matplotlib 优点: 功能强大:几乎可以用于绘制任何静态、动画和交互式图表。高度可定制&a…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
