uniapp遍历数组对象的常见方法
在 UniApp 中,遍历数组对象的方法与在普通 JavaScript 中是相同的。UniApp 是一个使用 Vue.js 开发所有前端应用的框架,因此你可以使用 Vue.js 和 JavaScript 的语法来遍历数组对象。
以下是一些常见的遍历数组对象的方法:
- 使用
for循环
let arr = [{ id: 1, name: 'Alice' },{ id: 2, name: 'Bob' },// ...
];for (let i = 0; i < arr.length; i++) {console.log(arr[i].id, arr[i].name);
}
- 使用
for...of循环 (ES6+ 语法)
let arr = [{ id: 1, name: 'Alice' },{ id: 2, name: 'Bob' },// ...
];for (let item of arr) {console.log(item.id, item.name);
}
- 使用
Array.prototype.forEach方法
let arr = [{ id: 1, name: 'Alice' },{ id: 2, name: 'Bob' },// ...
];arr.forEach(item => {console.log(item.id, item.name);
});
- 使用
Array.prototype.map方法 (虽然map通常用于生成新数组,但也可以用于遍历)
let arr = [{ id: 1, name: 'Alice' },{ id: 2, name: 'Bob' },// ...
];arr.map(item => {console.log(item.id, item.name);// 注意:map 会返回一个新数组,但在这里我们只是用它来遍历return null; // 可以返回任何值,但在这个例子中我们不需要新数组
});
- 使用 Vue 的
v-for指令 (在 UniApp 的模板中)
如果你在 UniApp 的模板中需要遍历数组对象,可以使用 v-for 指令:
<template><view><text v-for="(item, index) in arr" :key="index">{{ item.id }} - {{ item.name }}</text></view>
</template><script>
export default {data() {return {arr: [{ id: 1, name: 'Alice' },{ id: 2, name: 'Bob' },// ...]}}
}
</script>
注意:在 Vue 中使用 v-for 时,通常建议提供一个唯一的 :key 绑定,以帮助 Vue 跟踪每个节点的身份,从而重用和重新排序现有元素。在这个例子中,我使用了数组的索引作为键,但在实际应用中,如果可能的话,最好使用唯一的标识符(如 id)作为键。
相关文章:

uniapp遍历数组对象的常见方法
在 UniApp 中,遍历数组对象的方法与在普通 JavaScript 中是相同的。UniApp 是一个使用 Vue.js 开发所有前端应用的框架,因此你可以使用 Vue.js 和 JavaScript 的语法来遍历数组对象。 以下是一些常见的遍历数组对象的方法: 使用 for 循环 …...
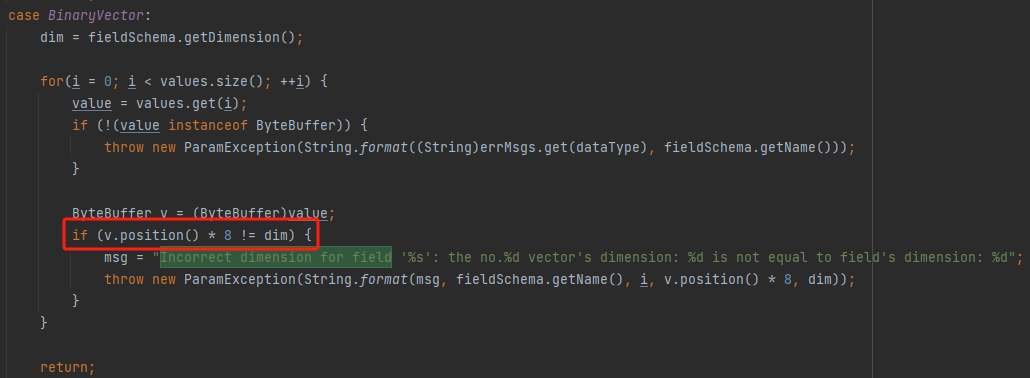
Milvus向量数据库(一)Milvus存储byte[]类型源向量数据
两种路线: 第一种是把byte[]转换为List< float >,然后存储到Milvus的floatVector中第二种是把byte[]转换为ByteBuffer,然后存储到Milvus的BinaryVector中 步骤: 我先用的是第一种,但是在转换float过程中&…...

Jupyter Notebook魔术命令
Jupyter Notebook是一个基于网页的交互式笔记本,支持运行多种编程语言。 Jupyter Notebook 的本质式一个Web应用程序,便于创建和共享文学化程序文档,支持实现代码,数学方程,可视化和markdown。用途包括:数据…...

python基础---生成器
生成器 这个老师的课 这个老师的网页 获取系列有规律但是个数不确定的数据 使用迭代器的时候可以使用一个不会产生异常的迭代器, 实际记录的是生成的数据的方式, 不是实际的数据 使用迭代器的时候这一个规则的改变不方便, 需要加一个专门的方法 还有就是如果需要大量的数据,…...
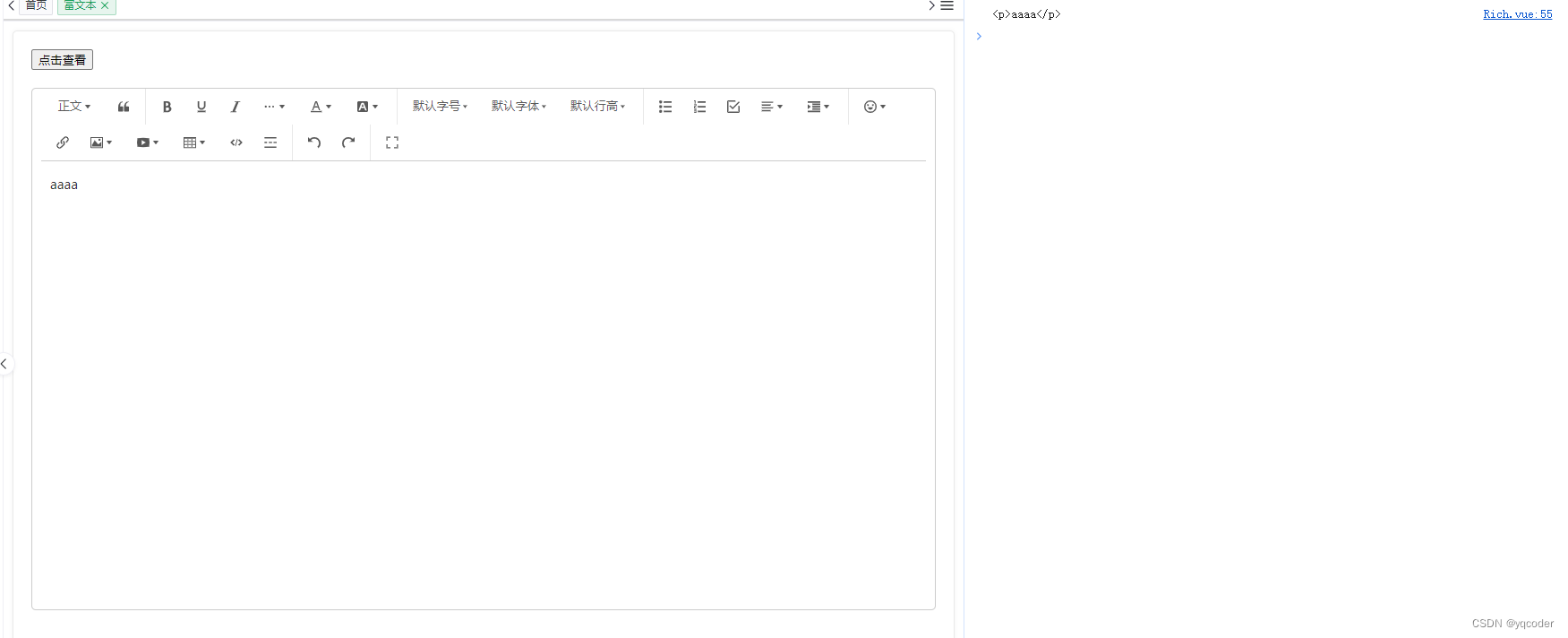
wangEditor 富文本详解
前言:wangEditor 官网 。本文档讲解 wangEditor 在 vue3 中的使用。 一:快速开始 1. 安装 需要安装 wangeditor/editor、wangeditor/editor-for-vuenext 两个依赖 # 安装 editor npm install wangeditor/editor # or yarn add wangeditor/editor # o…...
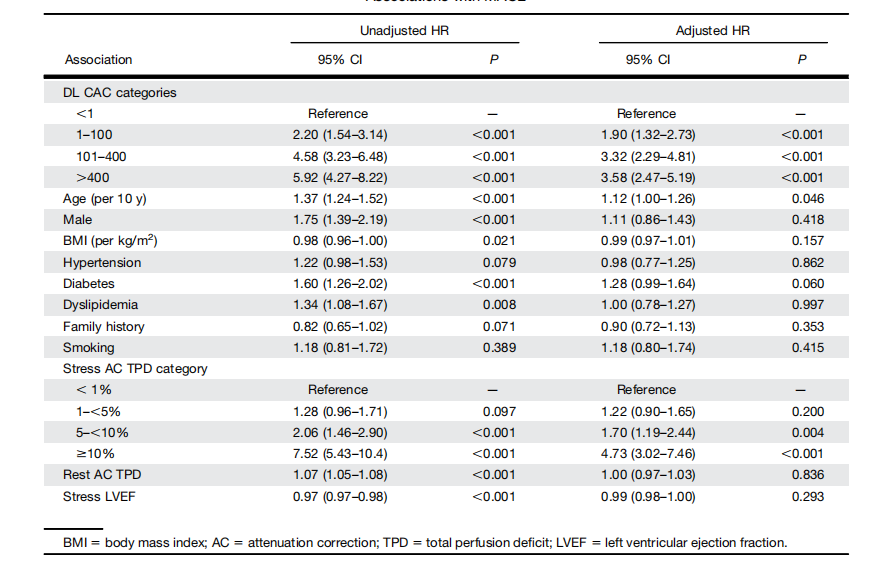
文献速递:深度学习医学影像心脏疾病检测与诊断--从SPECT/CT衰减图中深度学习冠状动脉钙化评分提高了对重大不良心脏事件的预测
Title 题目 Deep Learning Coronary Artery Calcium Scores from SPECT/CT Attenuation Maps Improve Prediction of Major Adverse Cardiac Events 从SPECT/CT衰减图中深度学习冠状动脉钙化评分提高了对重大不良心脏事件的预测 01 文献速递介绍 低剂量非门控CT衰减校正&am…...

Java多线程:常见的线程的创建方法及Thread类详解
目录 一.并发编程相关概念 线程与进程 多线程 Java中线程的状态 二.线程的创建方法 方法一:继承Thread类 方法二:实现Runnable接口 其他方法 三.Thread类详解 Thread常见构造方法 Thread常见属性 Thread常见方法 start() 与 run() sleep(…...

一招搞定生产管理
劳动力成本上升,原材料价格上涨,企业生产成本逐年增加,市场竞争越来越激烈,传统的中小制造企业面临着巨大的挑战。 企业的数字化转型如今成为炙手可热的高频词语,越来越多的中小制造企业已经开始上云,实践SaaS模式的生产管理系统…...

学习CSS3,实现红色心形loading特效
试想一下,如果你的网站在加载过程中,loading图由一个老旧的菊花转动图片,变为一个红色的心形loading特效,那该有多炫酷啊。 目录 实现思路 初始化HTML部分 延迟动画是重点 设定动画效果 完整源代码 最后 实现思路 每个…...
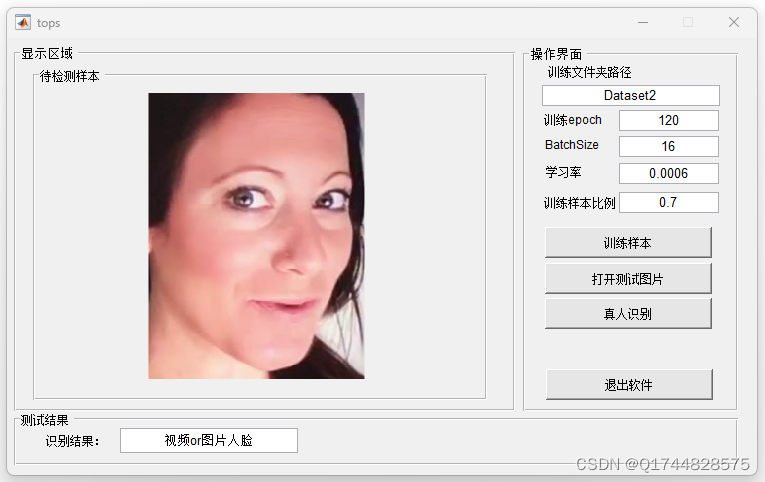
深度学习之基于Matlab神经网络的活体人脸和视频人脸识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景 人脸识别技术作为生物识别技术的一种,近年来得到了广泛的关注和应用。与传统的身份认证方…...

充电桩测试:负载箱的重要性
随着电动汽车的普及,充电桩的需求也在不断增加。为了保证充电桩的安全、稳定和高效运行,对其进行严格的测试是必不可少的。在充电桩测试过程中,负载箱作为一种重要的测试设备,对于评估充电桩的性能和可靠性具有重要意义。 负载箱可…...

贪心算法、Dijkstra和A*类路径搜索算法
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言系列文章目录前言1.贪心算法、Dijkstra和A*类路径搜索算法(1)greedy best frist search贪心算法(仅仅考虑启发式代价)1.核心思想2.构造启发式猜…...

Debian是什么?有哪些常用命令
目录 一、Debian是什么? 二、Debian常用命令 三、Debian和CentOS的区别 四、Debian和CentOS的优缺点 五、Debian和CentOS的运用场景 一、Debian是什么? Debian是一种流行的开源Linux操作系统。 Debian是一个以Linux内核为基础的操…...

万兴PDF专家 PDFelement Pro v10.3.8 破姐版!
🧑💻万兴PDF专家 PDFelement Pro v10.3.8 破姐版 (https://docs.qq.com/sheet/DRVVxTHJ3RXJFVHVr)...

Ubuntu22.04 私钥登录
1. 背景 以前一直使用秘钥登录Linux,最近新装了一台Ubuntu 22.04,照旧部署公钥,使用私钥登录,结果SecureCRT 登录没有问题,使用Xshell登录一直报“所选的用户密钥未在远程主机上注册,请再试一次”。然后各种试&#x…...

Java_JVM_JVMs
JVM 官方文档说明文档目录 官方文档 JVM Specification 说明 以Java SE 17为标准 文档目录 2:JVM 结构 class文件数据类型 基本数据类型引用数据类型 运行时数据区 栈帧 其他内容 对象的表示浮点数运算特殊方法 初始化方法【实例、类】多态方法 3ÿ…...
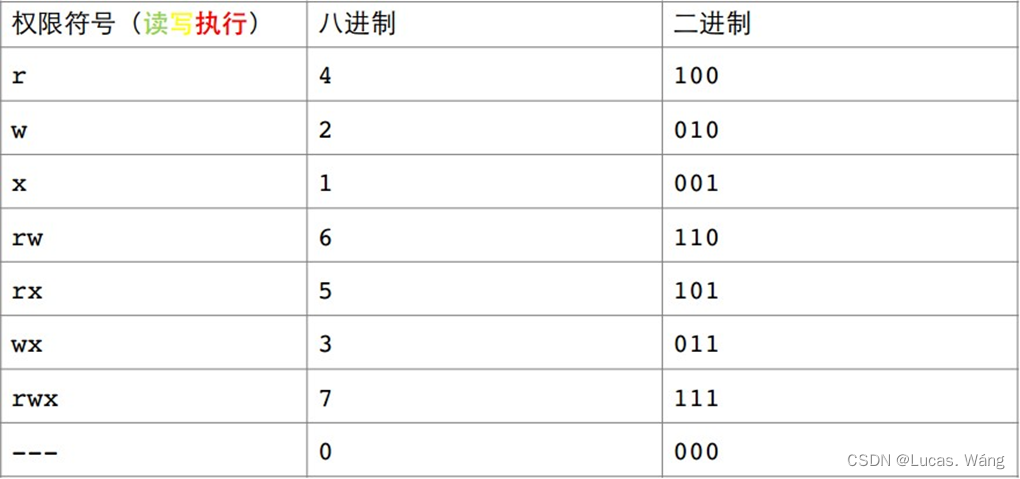
Linux系统编程之基本指令
零、Linux发展史 1、诞生 1991年10月5日,赫尔辛基大学的一名研究生Linus Benedict Torvalds在一个Usenet新闻组 (comp.os.minix)中宣布他编制出了一种类似UNIX的小操作系统,叫Linux。新的操作系统是受到另一个UNIX的小操作系统—…...
[1702]java旅游资源网上填报系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java旅游资源网上填报系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql…...

【Flask 系统教程 3】请求与响应
Flask 是一个灵活而强大的 Web 框架,而请求与响应则是构建 Web 应用的核心组成部分。在本文中,我们将探讨 Flask 中请求与响应的各种用法,包括不同的请求方法、重定向、响应对象、获取查询参数以及文件上传等。 请求 在 Flask 中࿰…...
jsp校园商城派送系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP 校园商城派送系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统采用serlvetdaobean mvc 模式,系统主要采用B/S模式 开发。开发环境为TOMCAT7.0,Myeclipse8.…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
