人脸美型SDK解决方案,适用于各类应用场景
视频内容已经成为企业宣传、产品展示、互动直播等多个领域的核心载体。而在这些场景中,高质量的人脸美型效果不仅能够提升用户体验,更能为品牌加分。美摄科技凭借深厚的技术积累和行业洞察,推出了全新的人脸美型SDK解决方案,为企业带来前所未有的视觉盛宴。
一、核心技术:人脸关键点检测与独特渲染引擎
美摄科技的人脸美型SDK解决方案,采用了自研的人脸关键点检测技术。该技术能够精准识别面部各个特征点,包括眉毛、眼睛、鼻子、嘴巴等,确保美型效果自然且符合人脸比例。与此同时,结合独有的渲染引擎,美摄科技在保证画质清晰度的同时,实现了丰富多样的美型效果,如磨皮、美白、瘦脸、大眼等,让每一位用户都能找到最适合自己的美颜方案。
二、优异性能:适用于各类场景
无论是在拍摄、直播还是编辑等场景中,美摄科技的人脸美型SDK都能展现出优异的性能。它支持高清、超清甚至4K等多种分辨率,确保在不同设备上都能获得流畅的体验。同时,SDK的轻量级设计使得它能够在不占用过多系统资源的情况下,实现高效的美型处理,满足企业对于性能的高要求。

三、广泛适用:满足企业多元化需求
美摄科技的人脸美型SDK解决方案广泛适用于各类企业。对于电商行业来说,通过实时美颜功能提升商品展示效果;对于娱乐直播平台而言,美颜功能能够增强主播的吸引力,提升用户黏性;而对于视频编辑软件而言,则能够为用户提供更多样化的编辑选项,满足其个性化需求。
四、定制化服务:量身打造最佳方案
美摄科技深知每个企业都有其独特的业务需求和品牌特色。因此,我们提供定制化的服务,根据企业的实际情况量身打造最适合的人脸美型SDK解决方案。无论是功能模块的定制、界面设计的优化还是技术支持的升级,我们都将全力以赴,确保企业能够获得最佳的使用体验。
美摄科技的人脸美型SDK解决方案以其卓越的技术实力、广泛的适用性和贴心的定制化服务赢得了众多企业的青睐。我们相信,在未来的发展中,美摄科技将继续秉承创新、专业、贴心的服务理念,为更多企业带来高质量的视频内容体验。让我们一起期待美摄科技在人脸美型领域的更多精彩表现吧!
相关文章:

人脸美型SDK解决方案,适用于各类应用场景
视频内容已经成为企业宣传、产品展示、互动直播等多个领域的核心载体。而在这些场景中,高质量的人脸美型效果不仅能够提升用户体验,更能为品牌加分。美摄科技凭借深厚的技术积累和行业洞察,推出了全新的人脸美型SDK解决方案,为企业…...

RS2103XH 功能和参数介绍及规格书
RS2103XH 是一款单刀双掷(SPDT)模拟开关芯片,主要用于各种模拟信号的切换和控制。下面是一些其主要的功能和参数介绍: 主要功能特点: 模拟信号切换:能够连接和断开模拟信号路径,提供灵活的信号路…...
nn.TransformerEncoderLayer详细解释,使用方法!!
nn.TransformerEncoderLayer nn.TransformerEncoderLayer 是 PyTorch 的 torch.nn 模块中提供的一个类,用于实现 Transformer 编码器的一个单独的层。Transformer 编码器层通常包括一个自注意力机制和一个前馈神经网络,中间可能还包含层归一化ÿ…...

巨控GRM561/562/563/564Q杀菌信息远程监控
摘要 通过程序编写、手机APP画面制作等运行系统,实现电脑及手机APP显示的历史曲线画面和数据图形化的实时性。 不仅流程效率提升90%以上,同时为杀菌生产提供有利的质量保障,还有效规避因触屏及内存卡的突发异常导致历史数据的丢失࿰…...

RT-DETR-20240507周更说明|更新Inner-IoU、Focal-IoU、Focaler-IoU等数十种IoU计算方式
RT-DETR改进专栏|包含主干、模块、注意力、损失函数等改进 专栏介绍 本专栏包含模块、卷积、检测头、损失等深度学习前沿改进,目前已有改进点70!每周更新。 20240507更新说明: ⭐⭐ 更新CIoU、DIoU、MDPIoU、GIoU、EIoU、SIoU、ShapeIou、PowerfulIoU、…...

Web3:下一代互联网的科技进化
随着科技的不断演进,互联网已经成为了我们生活中不可或缺的一部分。而在Web3时代,我们将会见证互联网进化的下一个阶段。本文将探讨Web3作为下一代互联网的科技进化,以及它所带来的重要变革和影响。 传统互联网的局限性 传统互联网存在诸多…...
SQL注入-基础知识
目录 前言 一,SQL注入是什么 二,SQL注入产生的条件 三,学习环境介绍 四、SQL注入原理 五,SQL中常用的函数 六,关于Mysql数据库 前言 在网络安全领域中,sql注入是一个无法被忽视的关键点,…...

npx 有什么作用跟意义?为什么要有 npx?什么场景使用?
npx 是 npm 从 v5.2.0 开始新增了 npx 命令,> 该版本会自动安装 npx,如果不能使用就手动安装一下: $ npm install -g npxnpx 的作用 npm 只能管理包的依赖,npx 则可以快捷的运用包中的命令行工具和其他可执行文件,…...
Docker搭建LNMP+Wordpress
目录 一.项目模拟 1.项目环境 2.服务器环境 3.任务需求 (1)使用 Docker 构建 LNMP 环境并运行 Wordpress 网站平台 (2)限制 Nginx 容器最多使用 500MB 的内存和 1G 的 Swap (3)限制 Mysql 容器写 /d…...

PCIE相关总结
1、概述 "PCIE 槽位" 指的是主板上的 Peripheral Component Interconnect Express (外围设备互联扩展)槽位。它是用于连接扩展卡(如显卡、网卡、声卡等)到主板的接口。PCI Express 是一种高速串行扩展总线标准ÿ…...
OpenCV 入门(五) —— 人脸识别模型训练与 Windows 下的人脸识别
OpenCV 入门系列: OpenCV 入门(一)—— OpenCV 基础 OpenCV 入门(二)—— 车牌定位 OpenCV 入门(三)—— 车牌筛选 OpenCV 入门(四)—— 车牌号识别 OpenCV 入门…...

C++基础-编程练习题2
文章目录 前言一、查找“支撑数”二、数组元素的查找三、爬楼梯四、数字交换五、找高于平均分的人 前言 C基础-编程练习题和答案 一、查找“支撑数” 【试题描述】 在已知一组整数中, 有这样一种数非常怪, 它们不在第一个, 也不在最后一个&…...
Linux下GraspNet复现流程
Linux,Ubuntu中GraspNet复现流程 文章目录 Linux,Ubuntu中GraspNet复现流程1.安装cuda和cudnn2.安装pytorch3.编译graspnetAPIReference 🚀非常重要的环境配置🚀 ubuntu 20.04cuda 11.0.1cudnn v8.9.7python 3.8.19pytorch 1.7.0…...

Linux——MySQL5.7编译安装、RPM安装、yum安装
文章目录 Linux——MySQL5.7编译安装、RPM安装、yum安装一、编译安装二、RPM安装三、yum安装 Linux——MySQL5.7编译安装、RPM安装、yum安装 卸载mysql # 查看是否安装了mysql [rootcsq ~]# rpm -qa |grep mysql mysql-community-server-5.7.36-1.el7.x86_64 mysql-community-c…...
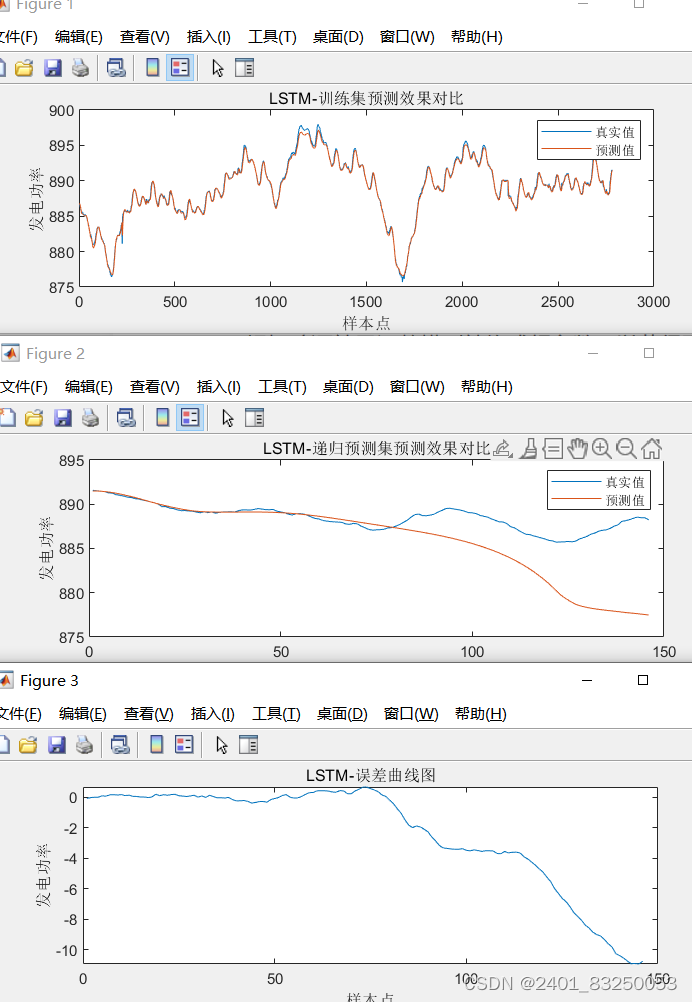
LSTM递归预测(matlab)
LSTM(长短期记忆)递归预测原理及步骤详解如下: LSTM递归预测(matlab)代码获取戳此处代码获取戳此处代码获取戳此处 一、LSTM递归预测原理 LSTM是一种特殊的递归神经网络(RNN),它能够…...
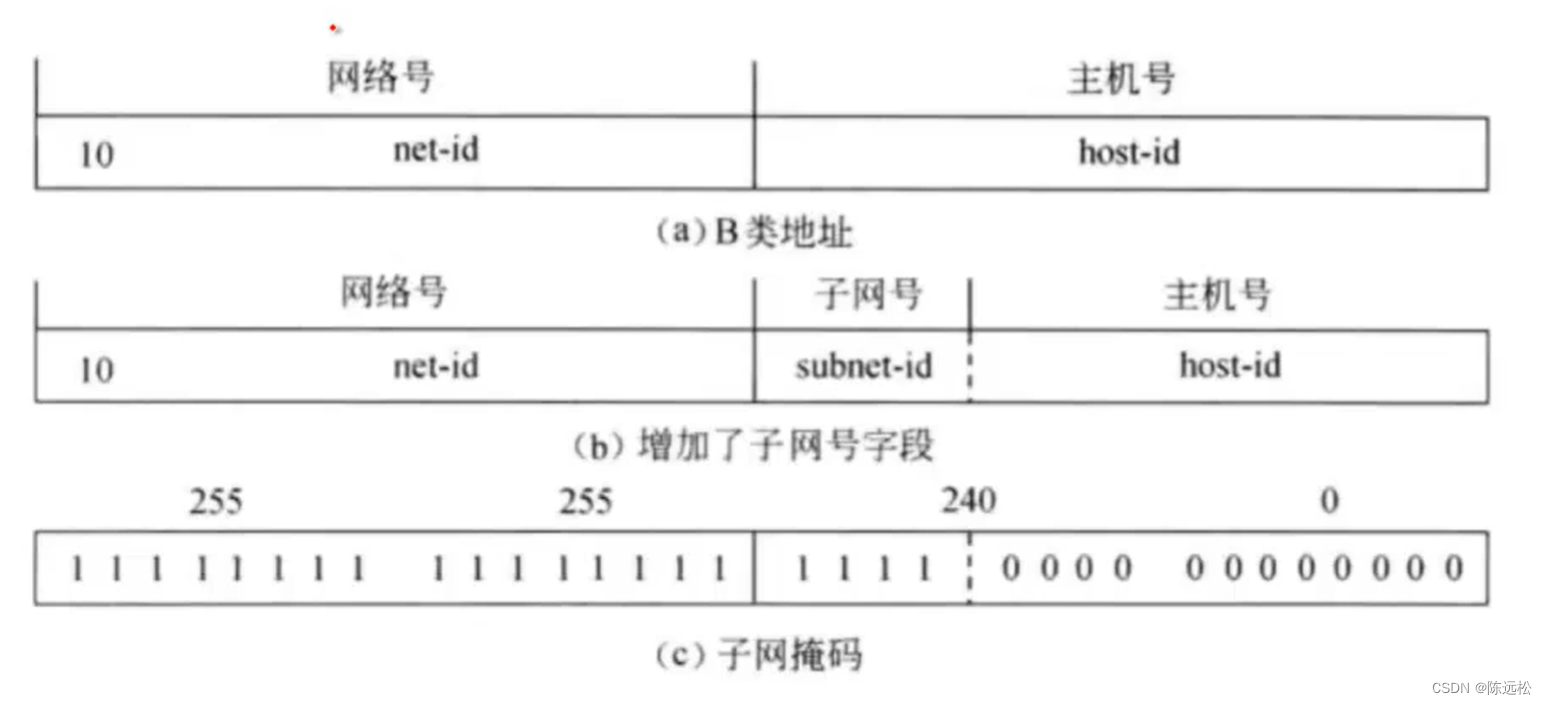
计算机网络 备查
OSI 七层模型 七层模型协议各层实现的功能 简要 详细 TCP/IP协议 组成 1.传输层协议 TCP 2.网络层协议 IP 协议数据单元(PDU)和 封装 数据收发过程 数据发送过程 1. 2.终端用户生成数据 3.数据被分段,并加上TCP头 4.网络层添加IP地址信息…...

查看软件包依赖关系
列出软件包依赖文件列表 rpm -ql 命令用于列出已安装软件包的文件列表。它显示软件包中包含的文件及其对应的路径。 具体来说,-q 选项表示查询已安装的软件包,而 -l 选项表示列出软件包中的文件列表。 例如,如果要查看已安装的 nginx 软件…...
 函数的用法)
C++ 中 strcmp(a,b) 函数的用法
【C 中 strcmp(a,b) 函数的用法】 ● 若 len(a)>len(b),则返回1。 ● 若 len(a)len(b),则返回0。 ● 若 len(a)<len(b),则返回-1。【C 中 strcmp(a,b) 函数的用法代码一】 #include <bits/stdc.h> using namespace std;int main…...
Servlet(一些实战小示例)
文章目录 一、实操注意点1.1 代码修改重启问题1.2 Smart Tomcat的日志1.3 如何处理错误 一. 抓自己的包二、构造一个重定向的响应,让页面重定向到百度主页三、让服务器返回一个html数据四、表白墙4.1 约定前后端数据4.2 前端代码4.3 后端代码4.4 保存在数据库的版本…...
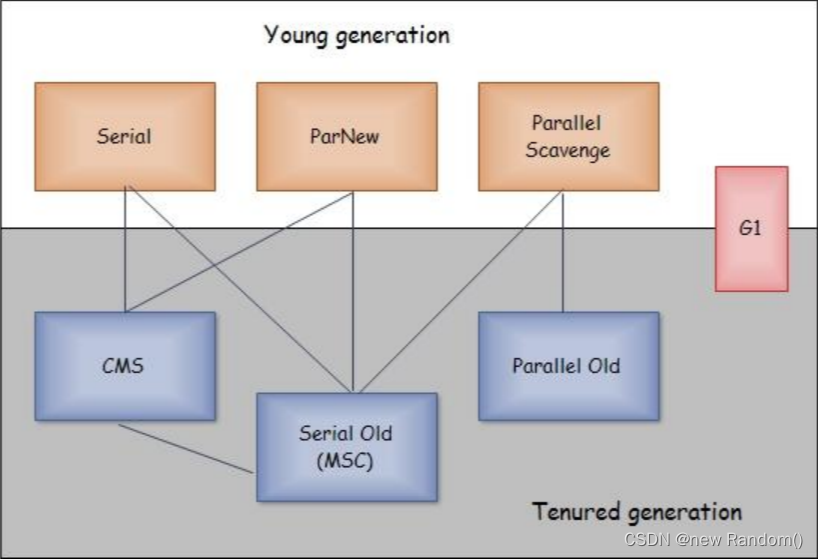
【JVM】垃圾回收机制(Garbage Collection)
目录 一、什么是垃圾回收? 二、为什么要有垃圾回收机制(GC)? 三、垃圾回收主要回收的内存区域 四、死亡对象的判断算法 a)引用计数算法 b)可达性分析算法 五、垃圾回收算法 a)标记-清除…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
