代码随想录day56 | 动态规划P16 | ● 583. ● 72. ● 编辑距离总结篇
583. 两个字符串的删除操作
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
示例 1:
输入: word1 = "sea", word2 = "eat" 输出: 2 解释: 第一步将 "sea" 变为 "ea" ,第二步将 "eat "变为 "ea"
示例 2:
输入:word1 = "leetcode", word2 = "etco" 输出:4
思路
动态规划1
定义dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
递推:
还是分为当前相等/不相等
相等则dp[i][j] = dp[i - 1][j - 1];(不需要删除,次数不涨)
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1(这里的+1是删除i-1)
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1(这里的+1是删除j-1)
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
初始化: 按照dp定义 首列初始化为列下标 首行初始化为行下标
动态规划2
求两字符串的最大公共子序列的长度, 然后用字符串长度去减
那么求最大公共子序列:
定义:dp[i][j] 表示以0 到 i-1为的字符串word1,和以 0 到 j-1位的字符串word2两字符串的最长公共子序列长度
递推:
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
初始化:按照dp定义 全0即可
代码
动态规划1
class Solution {public int minDistance(String word1, String word2) {//dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。int [][] dp = new int [word1.length()+1][word2.length()+1];for(int i = 0; i <= word1.length(); i++){dp[i][0] = i;}for(int j = 0; j<= word2.length(); j++){dp[0][j] = j;}for(int i = 1; i <= word1.length();i++){for(int j = 1; j<=word2.length(); j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1];}else{//dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2dp[i][j] = Math.min(dp[i][j-1] + 1, dp[i-1][j] + 1);}}}return dp[word1.length()][word2.length()];}
}动态规划2
class Solution {public int minDistance(String word1, String word2) {//dp[i][j] 表示以0 到 i-1为的字符串word1,和以 0 到 j-1位的字符串word2两字符串的最长公共子序列长度int [][] dp = new int [word1.length()+1][word2.length()+1];for(int i = 1; i <= word1.length();i++){for(int j = 1; j<=word2.length(); j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);}}}return word1.length() + word2.length() - 2 * dp[word1.length()][word2.length()] ;}
}72. 编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
思路
定义:dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
递推:
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了,怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:
a a d+-----+-----+ +-----+-----+-----+| 0 | 1 | | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
初始化:按照dp定义 首列初始化为列下标 首行初始化为行下标
代码
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length(), len2 = word2.length();//word1 0到i-1转为 word2 0到j-1的最少操作数int [][] dp = new int [len1 + 1][len2 + 1];for(int i = 0; i <= len1 ; i++){dp[i][0] = i;}for(int j = 0; j <= len2; j++){dp[0][j] = j;}for(int i = 1; i<=len1; i++){for(int j = 1; j<= len2; j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1];}else{int del1 = dp[i-1][j] + 1; // 删除word1中字符i-1int del2 = dp[i][j-1] + 1; // 删除word2中字符j-1//删除某个word中的字符 与 在另一个word中添加 是等价的 故只需要计算删除即可int rep = dp[i-1][j-1] + 1; //替换字符int min = Math.min(del1, del2);min = Math.min(min, rep);dp[i][j] = min;}}}return dp[len1][len2];}
}编辑距离总结篇
代码随想录 (programmercarl.com)
相关文章:

代码随想录day56 | 动态规划P16 | ● 583. ● 72. ● 编辑距离总结篇
583. 两个字符串的删除操作 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 &quo…...

ASP.NET网络在线考试系统
摘 要 随着计算机技术的发展和互联网时代的到来,人们已经进入了信息时代,也有人称为数字化时代。数在数字化的网络环境下,学生希望得到个性化的满足,根据自己的情况进行学习,同时也希望能够得到科学的评价,…...

天锐绿盾 | 办公加密系统,源代码防泄密、源代码透明加密、防止开发部门人员泄露源码
天锐绿盾作为一款专注于数据安全与防泄密的专业解决方案,它确实提供了针对源代码防泄密的功能,帮助企业保护其核心的知识产权。 PC地址: https://isite.baidu.com/site/wjz012xr/2eae091d-1b97-4276-90bc-6757c5dfedee 以下是天锐绿盾可能采…...
Day1| Java基础 | 1 面向对象特性
Day1 | Java基础 | 1 面向对象特性 基础补充版Java中的开闭原则面向对象继承实现继承this和super关键字修饰符Object类和转型子父类初始化顺序 多态一个简单应用在构造方法中调用多态方法多态与向下转型 问题回答版面向对象面向对象的三大特性是什么?多态特性你是怎…...

Spring 事务失效的几种情况
目录 1. 事务方法不是public 2. 自调用问题 3. 异常处理不当 4. 数据源或事务管理器配置错误 5. 事务传播行为不当 6. 代理方式不正确 7. 事务同步问题 1. 事务方法不是public 在Spring中,默认情况下,只有public方法上的Transactional注解才会被代…...
【Linux 命令操作】如何在 Linux 中使用多行注释呢?
文章目录 1. 给代码进行多行注释2. 给代码取消多行注释 1. 给代码进行多行注释 🐧① 首先用 vim 打开代码,按 Esc进入命令模式(Normal mode); 🐧② 然后按住 ctrl v 进入列模式; 🐧③ 再通过按 h(左)、j(…...

【RPC】Dubbo接口测试
关于rpc,推荐看看这篇 : 既然有HTTP协议,为什么还要有RPC 一、Dubbo 是一款alibaba开源的高性能服务框架: 分布式服务框架高性能和透明化的RPC远程服务调用方案SOA服务治理方案 二、Dubbo基础架构 三、 Dubbo接口测试 1、jme…...

PVZ2 植物克僵尸【第二期】
众所周知,PVZ2(植物大战僵尸2)中有许多恶心的僵尸,而我们不得不派出它们的————克星!(*为建议方法) 5.战机小鬼 战机小鬼,恶心会发射子弹,所以: 1&…...

libcity笔记:libcity/data/batch.py
1 Batch 2 BatchPAD...

【Java EE】多线程(二)Thread 类与常用方法
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 |《MySQL探索之旅》 |《Web世界探险家》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更…...

AGV无人叉车 | 我们为什么要投资“智慧生产”
AGV 作为一种智能工业车辆机器人,无人叉车充分融合叉车技术和AGV技术,近年来在仓储物流领域的应用逐步扩大。在传统叉车厂商、传统AGV厂商、物流集成商及仓储机器人企业等各方力量推动下,无人叉车市场在竞合中快速发展,并促使无人…...
【C++】滑动窗口:将x减到0的最小操作数
1.题目 2.算法思路 这个题目难在要转化一下才能用滑动窗口。 题意是需要在数组的前后两段区间进行解题,但同时对两段区间进行操作是比较困难的,我们可以将中间这段区间只和与nums_sum-x(数组总和-x)进行比较,这样就可…...
运动控制“MC_MoveVelocity“功能块详细应用介绍
1、运动控制单位u/s介绍 运动控制单位[u/s]介绍-CSDN博客文章浏览阅读91次。运动控制很多手册上会写这样的单位,这里的u是英文单词unit的缩写,也就是单位的意思,所以这里的单位不是微米/秒,也不是毫米/秒,这里是一个泛指,当我们的单位选择脉冲时,它就是脉冲/秒,也就是…...
9种单片机常用的软件架构
长文预警,加代码5000多字,写了4个多小时,盘软件架构,这篇文章就够了! 可能很多工程师,工作了很多年,都不会有软件架构的概念。 因为我在做研发工程师的第6年,才开始意识到这个东西,在…...
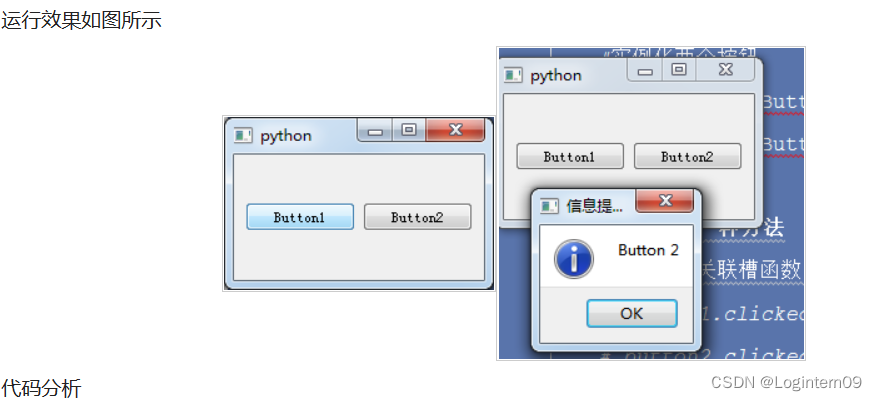
PyQt5中重要的概念:信号与槽
PyQt中信号与槽概念定义如下(网络上引用的): 信号(signal)和槽(slot)是Qt的核心机制,也是在PyQt编程中对象之间进行通信的机制。在创建事件循环之后,通过建立信号和槽的…...
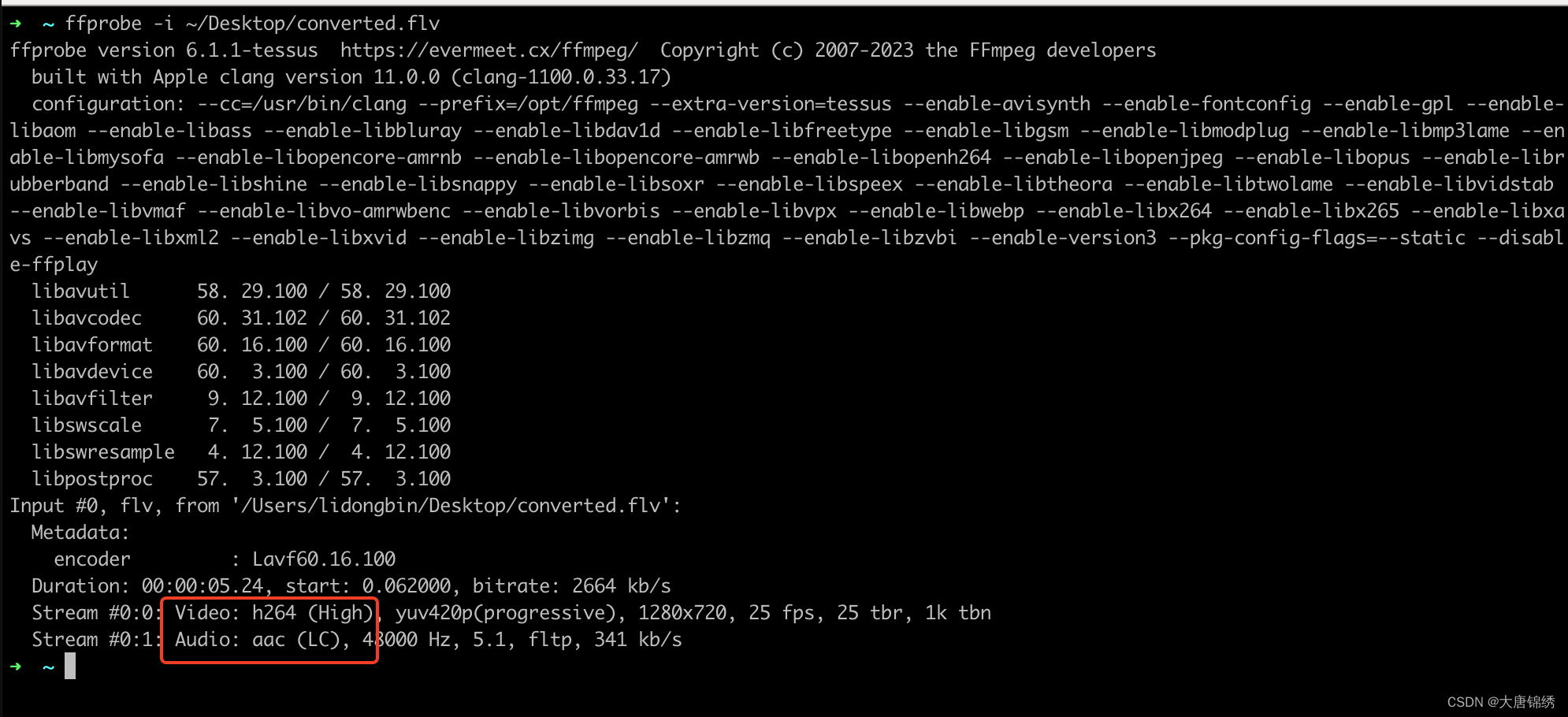
MacOS快速安装FFmpeg,并使用FFmpeg转换视频
前言:目前正在接入flv视频流,但是没有一个合适的flv视频流地址。网上提供的flv也都不是H264AAC(一种视频和音频编解码器组合),所以想通过fmpeg来将flv文件转换为H264AAC。 一、MacOS环境 博主的MacOS环境(…...
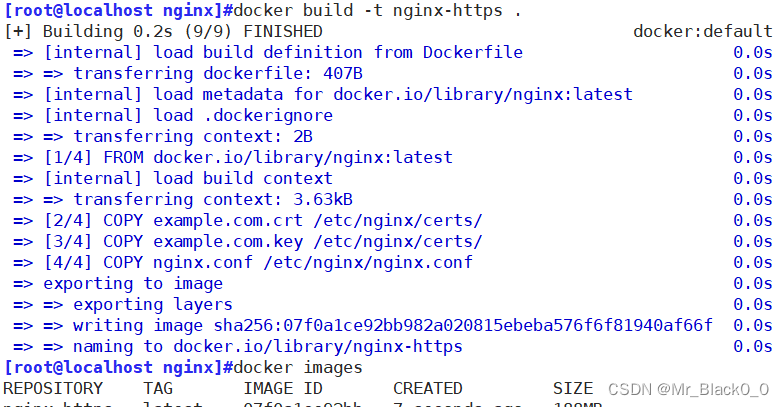
docker部署nginx并配置https
1.准备SSL证书: 生成私钥:运行以下命令生成一个私钥文件。 生成证书请求(CSR):运行以下命令生成证书请求文件。 生成自签名证书:使用以下命令生成自签名证书。 openssl genrsa -out example.com.key 2048 …...

五一小长假,景区智慧公厕发挥了那些作用?
五一小长假已经过去,在旅途中相信大家非常开心,其中也不乏一些细节让你有了更好的体验,而在您享受美景、畅游风光的同时,或许并未留意到那个角落里,默默为您服务的智慧公厕。是的,它们将成为您旅途中不可或…...
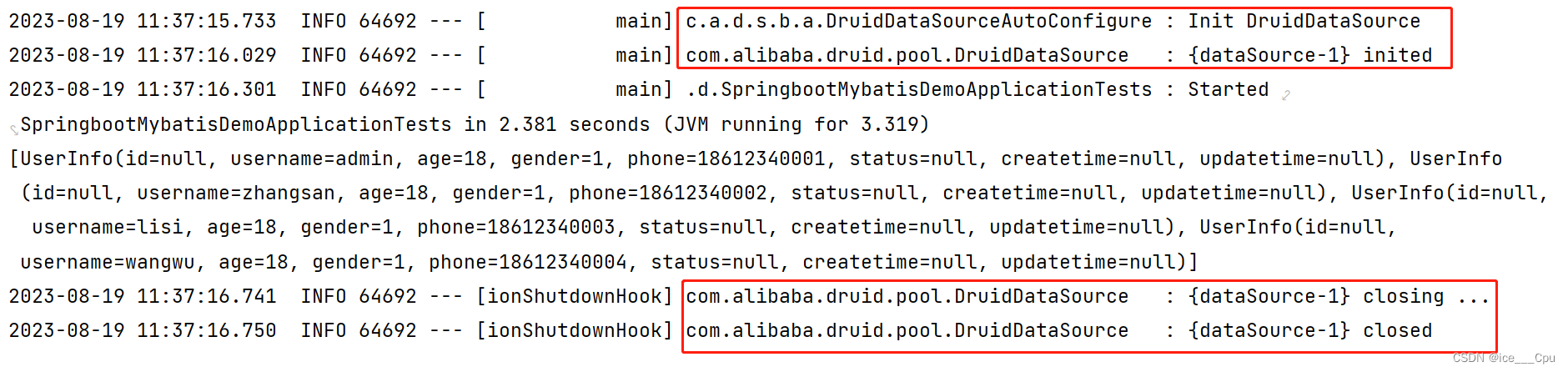
Spring - 9 ( 10000 字 Spring 入门级教程 )
一: MyBatis XML 配置文件 Mybatis 的开发有两种方式: 注解XML 我们已经学习了注解的方式, 接下来我们学习 XML 的方式 MyBatis XML 的方式需要以下两步: 配置数据库连接字符串和 MyBatis写持久层代码 1.1 配置连接字符串和 MyBatis 此步骤需要进…...

shpfile转GeoJSON;控制shp转GeoJSON的精度;如何获取GeoJSON;GeoJSON是什么有什么用;GeoJSON结构详解(带数据示例)
目录 一、GeoJSON是什么 二、GeoJSON的结构组成 2.1、点(Point)数据示例 2.2、线(LineString)数据示例 2.3、面(Polygon)数据示例 2.4、特征(Feature)数据示例 2.5、特征集合&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
