二分图(染色法与匈牙利算法)
二分图当且仅当一个图中不含奇数环
1.染色法
简单来说,将顶点分成两类,边只存在于不同类顶点之间,同类顶点之间没有边。
e.g.
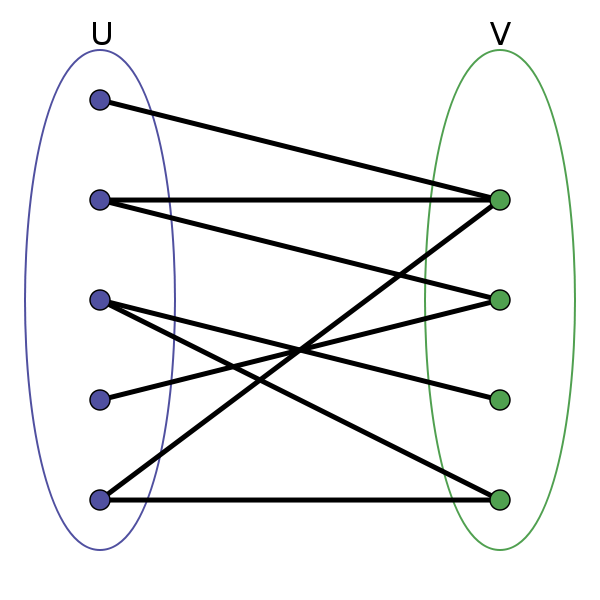
如果判断一个图是不是二分图?
开始对任意一未染色的顶点染色。
判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色。
若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断。
bfs和dfs可以搞定!
注意:如果有三个点另外成环,整个环是一个孤立环,其他都满足二分图,但是这个孤立不满足二分图,二分图的点不一定连通。所以要遍历每一个点。
1.dfs思路:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=200010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int n,m;
int color[N];
void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}
bool dfs(int a,int c){color[a]=c;for(int i=h[a];i!=-1;i=ne[i]){int j=e[i];if(!color[j]){if(!dfs(j,3-c)){return false;}}else{if(color[j]==c){return false;}}}return true;
}
int main(){memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i=1;i<=n;i++){if(!color[i]){if(!dfs(i,1)){puts("No");return 0;}}}puts("Yes");return 0;
}2.bfs思路:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=200010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int n,m;
int color[N];queue<int> q;
void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}
bool bfs(int a){color[a]=1;q.push(a);while(q.size()){auto t=q.front();q.pop();for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(!color[j]){color[j]=3-color[t];q.push(j);}else if(color[j]==color[t]) return false;}}return true;
}
int main(){memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i=1;i<=n;i++){if(!color[i]){if(!bfs(i)){puts("No");return 0;}}}puts("Yes");return 0;
}2.匈牙利算法
要了解匈牙利算法必须先理解下面的概念:
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
这篇文章把这个算法讲的很有意思:
趣写算法系列之--匈牙利算法_匈牙利算法基本原理-CSDN博客
简单来说就是:
遍历所有男生
让该男生考虑所有心动女生
如果当前女生单身,或者该女生的对象找了备胎,该女生就接受该男生
最坏时间复杂度 O(nm),和其它最大流问题一样,实际比较快
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 100010;int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool find(int x){for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];if(!st[j]){st[j]=1;if(match[j]==0||find(match[j])){match[j]=x;return true;}}}return false;
}
int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, false, sizeof st);if (find(i)) res ++ ;}printf("%d\n", res);return 0;
}在上述代码中,有一个令人费解的东西:就是st数组的作用,其实直白的理解:如果你每次不把st重新置为false,那剩下的人一看到前面的妹子st已经为true,不去让妹子的对象换掉这个妹子,直接就放弃了,会影响最后结果。
我们通过一个实际案例理解一下:
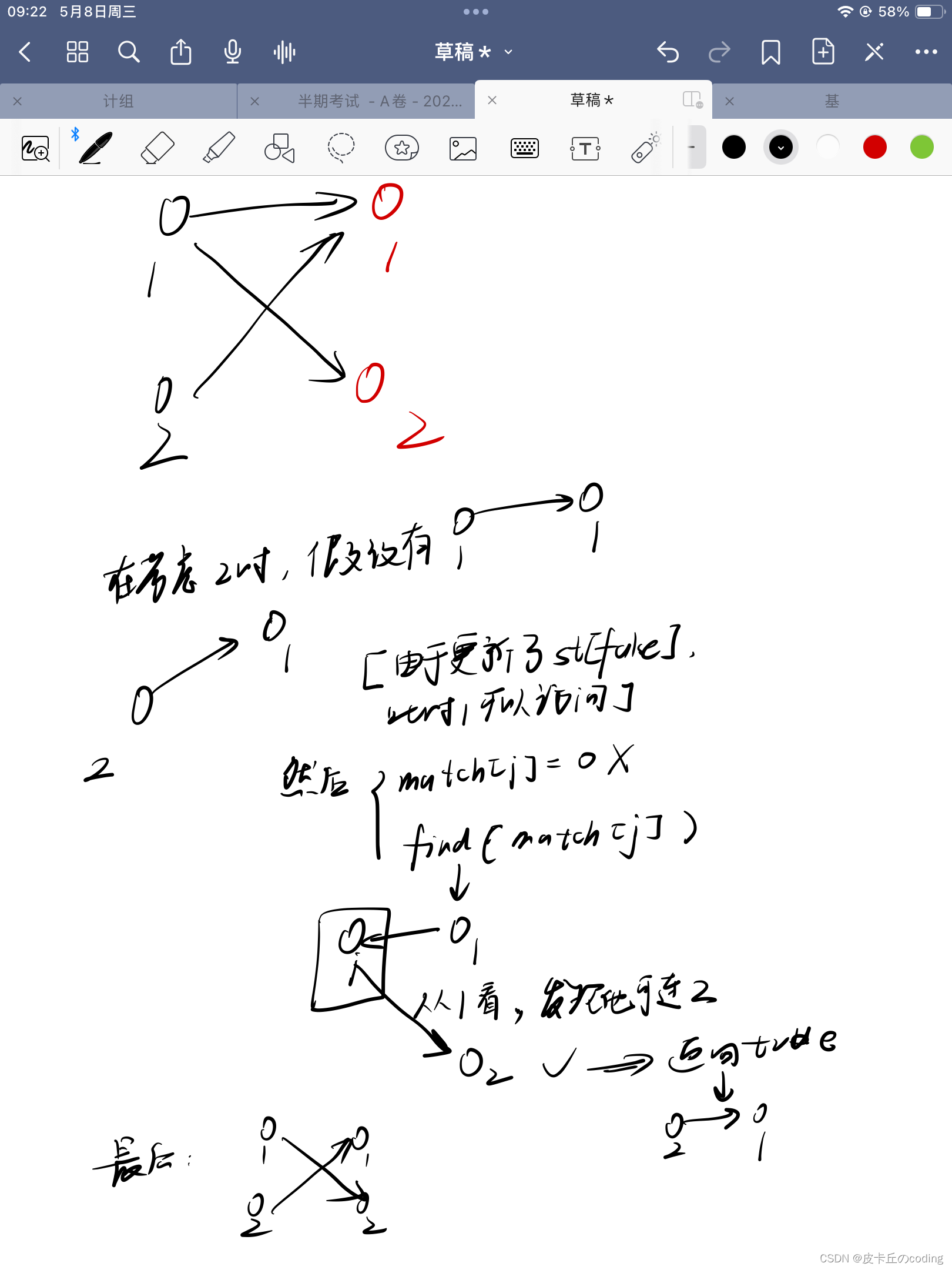
不难看出,st数组主要是在两个人连接了一个妹子的的时候才有用, 这个st的存在,让find在本次找的时候,原来的那个男生,不会再找这个妹子,只会找其他的。
还有一种理解:st的理解可以参考操作系统中锁的概念。假如说左边的是进程,右边的是资源。当进程i要访问资源j时,为了避免其他进程在此时访问资源j,需要对资源j加一个“锁”,即st[j] = true。当进程i访问完资源时,为了让后续其他进程也能访问资源,需要把锁解开,即memset(st, false, sizeof st)。
相关文章:

二分图(染色法与匈牙利算法)
二分图当且仅当一个图中不含奇数环 1.染色法 简单来说,将顶点分成两类,边只存在于不同类顶点之间,同类顶点之间没有边。 e.g. 如果判断一个图是不是二分图? 开始对任意一未染色的顶点染色。 判断其相邻的顶点中,若未…...
ReactFlow的ReactFlow实例事件传参undefined处理状态切换
1.问题 ReactFlow的ReactFlow实例有些事件我们在不同的状态下并不需要,而且有时候传参会出现其它渲染效果,比如只读状态下我们不想要拖拉拽onEdgesChange连线重连或删除的功能。 2.思路 事件名称类型默认值onEdgesChange(changes: EdgeChange[]) >…...

Dockerfile 和 Docker Compose
Dockerfile 和 Docker Compose 是 Docker 生态系统中两个重要的组成部分,它们分别服务于不同的目的,但共同协助开发者和运维人员高效地管理和部署容器化应用。 Dockerfile Dockerfile 是一个文本文件,包含了构建 Docker 镜像所需的一系列指…...

多个文件 import 的相同模块里的对象
多个文件 import 的相同模块里的对象,是否永远都是同一个对象? 在store的index.js中 import vue from ‘vue’ import Vuex from ‘vuex’ 并配置有关对象 然后再app.vue中配置vm 在不同的文件中 import一个vue对象,在任何情况下&#…...

面试经典150题——验证回文串
面试经典150题 day25 题目来源我的题解方法一 双指针方法二 双指针 空间优化 题目来源 力扣每日一题;题序:125 我的题解 方法一 双指针 首先去除掉字符串中的无用字符,并将英文字符转换为小写,然后使用双指针来判断是否是回文串…...
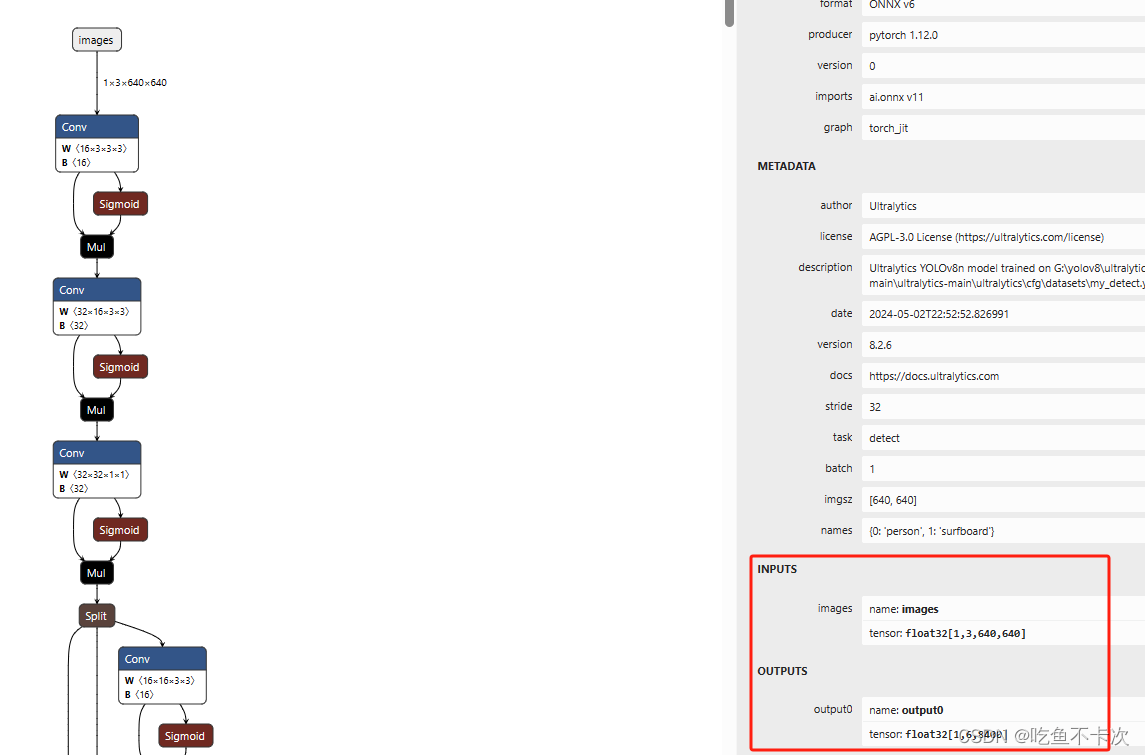
YOLOv8的训练、验证、预测及导出[目标检测实践篇]
这一部分内容主要介绍如何使用YOLOv8训练自己的数据集,并进行验证、预测及导出,采用代码和指令的两种方式,参考自官方文档:Detect - Ultralytics YOLOv8 Docs。实践篇不需要关注原理,只需要把流程跑通就行,…...

光伏远动通讯屏的组成
光伏远动通讯屏的组成 远动通讯屏主要用于电力系统数据采集与转发,远动通讯屏能够采集站内的各种数据,如模拟量、开关量和数字量等,并通过远动通讯规约将必要的数据上传至集控站或调度系统。这包括但不限于主变和输电线路的功率、电流、电压等…...
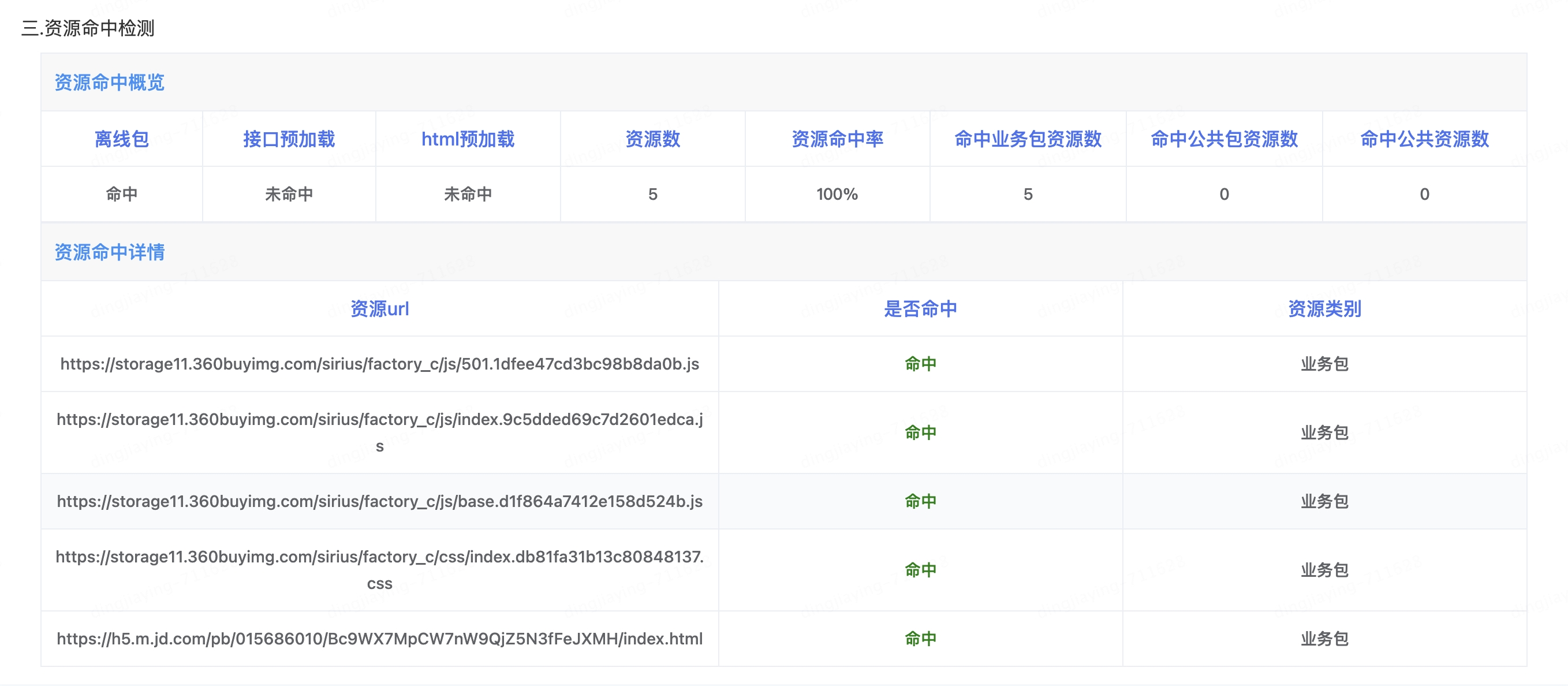
营销H5测试综述
H5页面是营销域最常见的一种运营形式,业务通过H5来提供服务,可以满足用户对于便捷、高效和低成本的需求。H5页面是业务直面用户的端点,其质量保证工作显得尤为重要。各业务的功能实现具有通用性,相应也有共性的测试方法࿰…...

【C++随记4】C++二进制位操作运算符
在C中,二进制位操作运算符允许你直接对整数类型的变量的位进行操作。这些运算符包括: 按位与(Bitwise AND): & 按位或(Bitwise OR): | 按位异或(Bitwise XOR): ^ 按位取反&…...
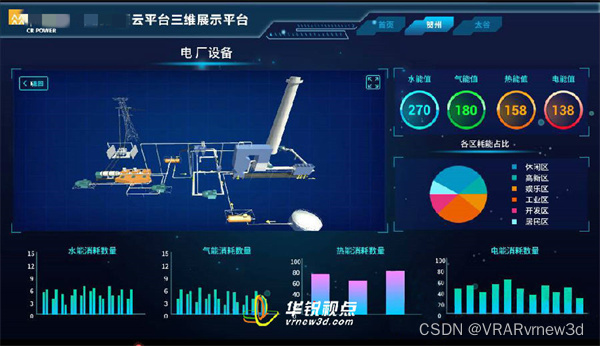
风电厂数字孪生3D数据可视化交互展示构筑智慧化电厂管理体系
随着智慧电厂成为未来电力企业发展的必然趋势,深圳华锐视点紧跟时代步伐,引领技术革新,推出了能源3D可视化智慧管理系统。该系统以企业现有的数字化、信息化建设为基础,融合云平台、大数据、物联网、移动互联、机器人、VR虚拟现实…...

大模型市场爆发式增长,但生成式AI成功的关键是什么?
进入2024年,大模型市场正在爆发式增长。根据相关媒体的总结,2024年1-4 月被统计到的大模型相关中标金额已经达到2023年全部中标项目披露金额的77%左右;其中,从项目数量来看,应用类占63%、算力类占21%、大模型类占13%、…...

leetcode LCR088.使用最小花费爬楼梯
思路:DP 这道题相对来说比较基础,但是有时候容易出错的一点就是在dp递推的时候,由于我们的思路是从最后一步向着初始状态推的,所以在编写程序的时候也容易就直接推着走了。其实实际上我们倒着想只是为了推理,真正要递…...

【DevOps】怎么提升Elasticsearch 的搜索性能
一、怎么提升Elasticsearch 搜索性能 提升 Elasticsearch (ES) 的搜索性能可以从多个角度进行优化,包括硬件选择、配置调整、查询优化等。以下是一些具体的方法和建议: 1. 硬件优化 使用 SSDs: 使用固态硬盘(SSD)而…...

启动任何类型操作系统:不需要检索 ISO 文件 | 开源日报 No.243
netbootxyz/netboot.xyz Stars: 7.7k License: Apache-2.0 netboot.xyz 是一个方便的平台,可以不需要检索 ISO 文件就能启动任何类型操作系统或实用工具磁盘。它使用 iPXE 提供用户友好的 BIOS 菜单,让您轻松选择所需的操作系统以及特定版本或可引导标志…...
Linux——综合实验
要求 按照上面的架构部署一个简单的web节点所有的服务器使用DNS服务器作为自己的DNS服务器 就是/etc/reslov.conf 中nameserver的值必须是途中dns服务器的地址所有的数据库都是用mysql应用 nfs共享导出在客户端(web服务器上)使用autofs在自动挂载,或者写入/etc/fsta…...

oracle数据库用户名修改
在Oracle数据库中,修改用户名通常涉及一系列步骤。以下是修改Oracle数据库用户名的详细步骤: 修改前准备工作: 使用ssh工具以root身份连接服务器。 切换到oracle用户:su - oracle(回车) 使用sqlplus连接数…...

2024年开抖音小店需要多少钱?你真的知道吗?最新入驻条件及费用
大家好,我是电商花花。 现在仍然有很多想开抖店,想做抖音小店,但是很多人都不知道投资一家抖音小店需要多少钱,今天花花就给大家讲一下做一家抖音小店需要投入多少资金,以及具体投入到哪些方面。 我们就说一下个体店…...
Vue创建todolist
电子书 第三章: https://www.dedao.cn/ebook/reader?idV5R16yPmaYOMqGRAv82jkX4KDe175w7xRQ0rbx6pNgznl9VZPLJQyEBodb89mqoO 没有使用VUE CLI创建项目。 创建步骤: 1, 用Vite 创建项目 2, npm run dev 运行程序 参照之前的文…...

了解Ansible Playbook
在现代IT运维中,自动化部署成为了提高效率、降低错误率的重要手段之一。而Ansible作为一种强大的自动化工具,其Playbook机制为自动化部署提供了灵活、可扩展的解决方案。本文将深入介绍Ansible Playbook的概念、结构、语法和常见用法,帮助读者…...
nginx 负载均衡、反向代理实验
nginx 负载均衡、反向代理实验 实验目的 理解概念:明确反向代理和负载均衡的基本概念及其在网络架构中的作用。 掌握技能:学习如何配置Nginx以实现反向代理和负载均衡功能。 实践应用:通过实际操作,体验Nginx如何提升Web服务的可…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
