当前位置： 首页 > news >正文

GIS入门，常用的多边形平滑曲线算法介绍和JavaScript的多边形平滑曲线算法库chaikin-smooth的实现原理和使用

news 2026/2/11 0:01:06

前言

本章介绍一下常用的多边形平滑曲线算法及其使用案例。
多边形平滑算法通常用于图形处理或计算机图形学中，以使线条或曲线在连接处平滑过渡，而不出现明显的棱角或断裂。多边形平滑算法有多种实现方法，其中一些常见的有下面几种：

  1. 贝塞尔曲线插值（Bezier Curve Interpolation）：使用贝塞尔曲线来插值原始线条的控制点，以获得平滑的转角效果。这种方法可以通过调整贝塞尔曲线的控制点来控制曲线的形状和平滑度。

贝塞尔曲线插值算法实际案例参考博主文章：《GIS入门，根据起止点和一个控制点计算二阶贝塞尔曲线（共三个控制点组成的线段转曲线）》

  1. 样条曲线（Spline Curve）：样条曲线是一种平滑的曲线，它通过一组插值点（节点）来定义。通过适当选择节点和插值方法，可以实现平滑的转角效果。

样条曲线（Spline Curve）插值算法实现案例参考博主文章：《GIS入门，不使用任何第三方库，纯JavaScript实现Catmull-Rom样条曲线（Spline Curve）插值算法，生成更加平

相关文章：

GIS入门，常用的多边形平滑曲线算法介绍和JavaScript的多边形平滑曲线算法库chaikin-smooth的实现原理和使用

前言 本章介绍一下常用的多边形平滑曲线算法及其使用案例。 多边形平滑算法通常用于图形处理或计算机图形学中，以使线条或曲线在连接处平滑过渡，而不出现明显的棱角或断裂。多边形平滑算法有多种实现方法，其中一些常见的有下面几种： 贝塞尔曲线插值（Bezier Curve Interpo…...

编程日记 2024/5/8 14:31:11

气膜体育馆内部的采光效果如何？—轻空间

气膜体育馆内部的采光效果如何？这是许多人对这种创新建筑的一个关键关注点。 首先，气膜体育馆的采光性非常好。阳光透过屋顶时以漫射光的方式进入室内，这种透射方式使得室内的光线柔和而均匀。从内部观察，整个屋顶就像一个连续的明…...

编程日记 2024/5/8 14:28:07

矩阵的对称正定性判决（复习）

文章目录 本科学的数学知识忘的太快了 如何判断一个实矩阵是否是对称正定 在线性代数中，一个实对称矩阵是否为正定可以通过以下方法判断： 对称性： 首先，确认矩阵是否对称，即矩阵的转置是否等于其本身。 特征值检查&…...

编程日记 2024/5/8 14:27:05

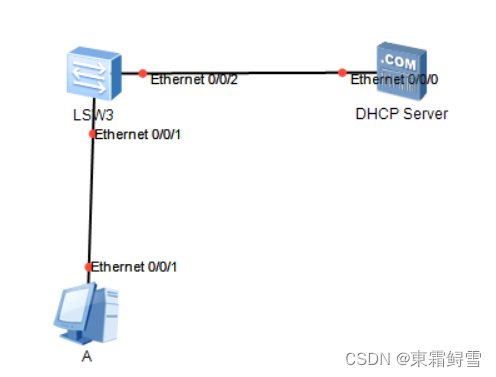
网络安全之DHCP详解

DHCP：Dynamic Host Configration Protocol 动态主机配置协议 某一协议的数据是基于UDP封装的，当它想确保自己的可靠性时，这个协议要么选确认重传机制，要么选周期性传输。 DHCP是确认重传，【UDP|DHCP】,当DHCP分配完地…...

编程日记 2024/5/8 14:25:03

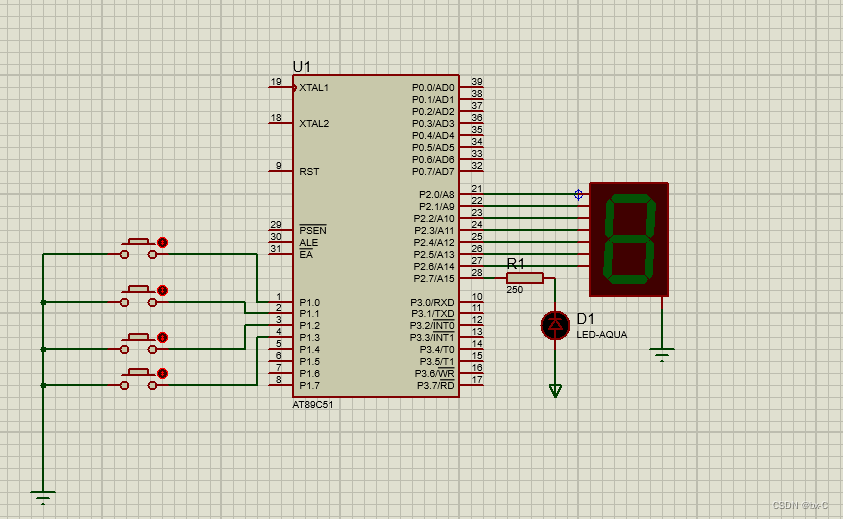
【Proteus】LED呼吸灯 直流电机调速

1.LED呼吸灯 #include <REGX51.H> sbit LEDP2^0; void delay(unsigned int t) {while(t--); } void main() {unsigned char time,i;while(1){for(time0;time<100;time){for(i0;i<20;i){LED0;delay(time);LED1;delay(100-time);}}for(time100;time>0;time--){fo…...

编程日记 2024/5/8 14:24:02

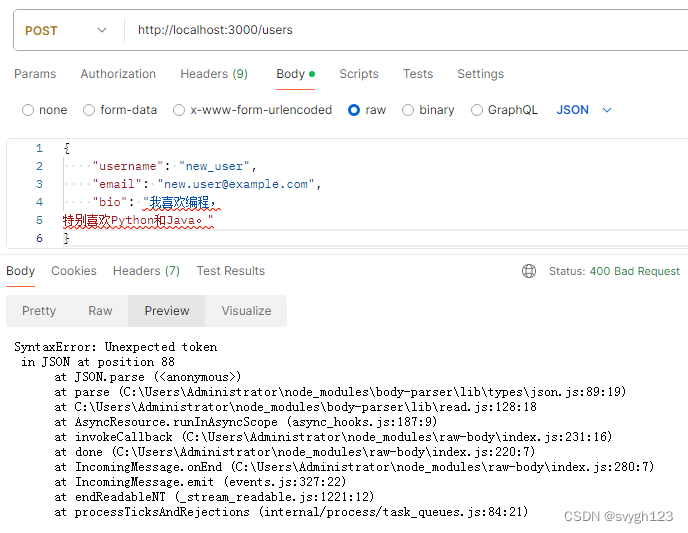
今天遇到一个GPT解决不了的问题

问题描述 你好&#xff0c;postman的一个post请求&#xff0c;编辑器里面放了一个很长的json数据&#xff0c;报Tokenization is skipped for long lines for performance reasons. This can be configured via editor.maxTokenizationLineLength.&#xff0c;但是同样的数据&a…...

编程日记 2024/5/8 14:23:00

优化SQL的方法

来自组内分享&#xff0c;包含了比较常使用到的八点&#xff1a; 避免使用select * union all代替union 小表驱动大表 批量操作 善用limit 高效的分页 用连接查询代替子查询 控制索引数量 一、避免使用select * 消耗数据库资源 消耗更多的数据库服务器内存、CPU等资源。 消…...

编程日记 2024/5/8 14:21:59

库存管理系统开源啦

软件介绍 ModernWMS是一个针对小型物流仓储供应链流程的开源库存管理系统。该系统的开发初衷是为了满足中小型企业在有限IT预算下对仓储管理的需求。通过总结多年ERP系统研发经验&#xff0c;项目团队开发了这套适用于中小型企业的系统&#xff0c;以帮助那些有特定需求的用户。…...

编程日记 2024/5/8 14:20:58

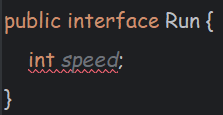
【java】接口

什么是接口 接口当中存在的是对方法的定义&#xff0c;而不是对方法的具体实现。 为什么不实现这个方法呢&#xff1f; 继承的本质是代码的复用。当一个父类会经常被继承&#xff0c;并且子类都要自己实现方法时&#xff0c;父类中的方法就会显得累赘&#xff0c;并且占用了…...

编程日记 2024/5/8 14:19:57

Java中的类型转换

一、类型转换 对类型转换来说分为向上类型转换和向下类型转换&#xff1a; 向上类型转换是自动完成的&#xff0c;一般是小类型向大类型转换。在引用类型中是子类型向父类型转换。向下类型转换是强制完成的&#xff0c;一般是大类型向小类型转换。在引用类型中是父类型向子类…...

编程日记 2024/5/8 14:17:54

定义范围对PFMEA分析的重要性——SunFMEA软件

在进行PFMEA分析时&#xff0c;定义范围是一个至关重要的步骤。这是因为&#xff0c;通过明确分析的范围&#xff0c;可以确保团队关注到最关键、最可能影响产品质量的过程&#xff0c;从而更有效地识别和解决潜在问题。今天SunFMEA软件和大家一起讨论定义范围对PFMEA操作的重要…...

编程日记 2024/5/8 14:15:51

json返回工具类|世界协调时间（UTC）

一、问题 世界协调时间&#xff08;UTC&#xff09;是一个标准的时间参考&#xff0c;通常被用于跨越不同时区的时间标准。要将 UTC 时间转换为中国时间&#xff08;中国标准时间&#xff09;&#xff0c;你需要将时间加上8个小时&#xff0c;因为中国位于 UTC8 时区。 初中知…...

编程日记 2024/5/8 14:14:50

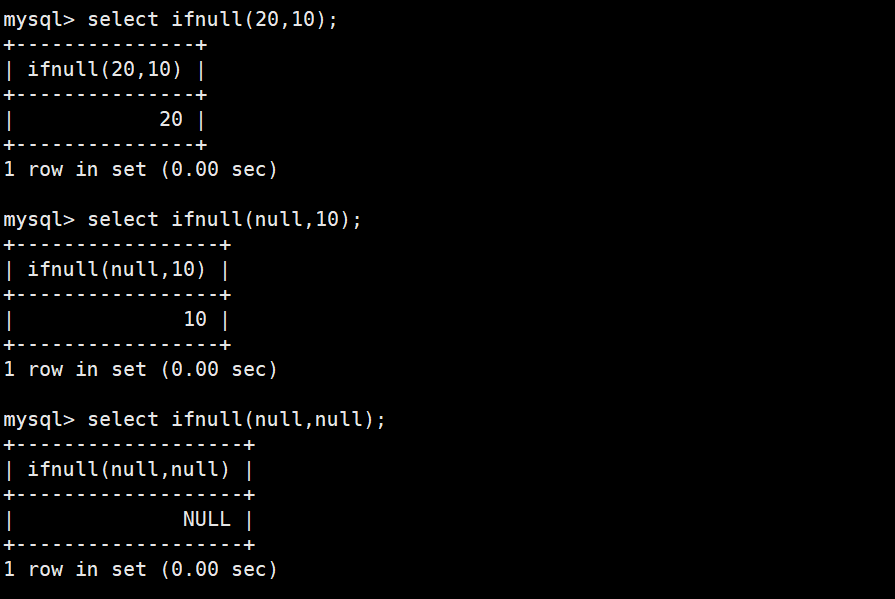
MySQL·内置函数

目录 函数 日期函数 案例1&#xff1a;创建一张表&#xff0c;记录生日 案例2&#xff1a;创建一个留言表 案例3&#xff1a;请查询在2分钟内发布的帖子 字符串函数 案例1&#xff1a; 获取emp表的ename列的字符集 案例2&#xff1a;要求显示exam_result表中的信息&am…...

编程日记 2024/5/8 14:13:47

vue根据文字动态判断溢出...鼠标悬停显示el-tooltip展示

使用自定义el- tooltip 组件 定义 Tooltip是一种小型弹出框，它显示有关特定页面元素的信息，例如按钮、链接或图标。Tooltip通常以半透明的气泡形式呈现，并出现在页面元素的旁边或下方。 它可以改善用户体验，使用户更容易理解页面元素的功能和意图。用户可以通过将鼠标悬停…...

编程日记 2024/5/8 14:12:45

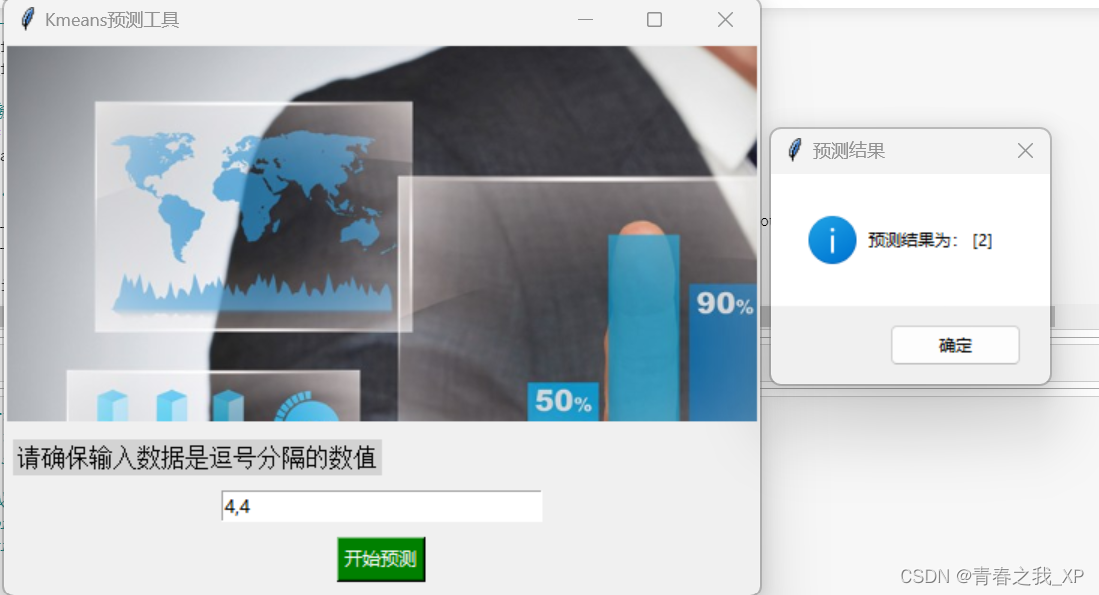
使用Tkinter实现数据预测工具的GUI界面展示

如果构建好预测模型后&#xff0c;想将预测模型通过一个交互式的页面显示&#xff0c;可以通过下边两种方式实现。 本文中代码有详细解析注释&#xff0c;便不再如往期一样分开讲解了&#xff0c;有需要的朋友可以直接拿去使用&#xff0c;代码可以直接运行&#xff0c;把预测…...

编程日记 2024/5/8 14:11:42

机器学习笔记-22

终章 至此吴恩达老师的机器学习课程已经完成啦&#xff0c;总结一下&#xff1a; 1.监督学习的算法&#xff1a;线性回归、逻辑回归、神经网络和向量机 2.无监督学习的算法&#xff1a;K-Means、PCA、异常检测 3.推荐系统、大规模数据处理、正则化、如何评估算法 4.上限分析、…...

编程日记 2024/5/8 14:08:36

车间为什么选择蒸发式冷风机？

蒸发式冷风机具有以下特点&#xff1a; 节能环保&#xff1a;蒸发式冷风机不使用压缩机和化学制冷剂&#xff0c;而是通过水的蒸发来降低温度&#xff0c;因此它是无压缩机、无冷媒、无污染的环保型产品。降温效果显著&#xff1a;在较潮湿地区&#xff0c;它一般能达到5-9℃的…...

编程日记 2024/5/8 14:07:34

5分钟速通大语言模型（LLM）的发展与基础知识

✍️ 作者&#xff1a;哈哥撩编程&#xff08;视频号同名&#xff09; 博客专家全国博客之星第四名超级个体COC上海社区主理人特约讲师谷歌亚马逊演讲嘉宾科技博主极星会首批签约作者 &#x1f3c6; 推荐专栏&#xff1a; &#x1f3c5; 程序员&#xff1a;职场关键角色通识宝…...

编程日记 2024/5/8 14:06:32

vue项目开发流程

vue项目开发流程 环境配置 asdf plugin add nodejs asdf install nodejs 16.20.2创建项目 npm create vitelatest my-vue-app -- --template vue npm install npm run dev修改调试端口 修改vite.config.js,修改如下所示&#xff0c;添加server的host和port。 import { de…...

编程日记 2024/5/8 14:03:28

【Django学习笔记（十）】Django的创建与运行

Django的创建与运行 前言正文1、安装Django2、创建项目2.1 基于终端创建项目2.2 基于Pycharm创建项目2.3 两种方式对比 3、默认项目文件介绍4、APP5、启动运行Django5.1 激活App5.2 编写URL和视图函数对应关系5.3 启动Django项目5.3.1 命令行启动5.3.2 Pycharm启动5.3.3 views.…...

编程日记 2024/5/8 14:02:27

FFmpeg 低延迟同屏方案

引言 在实时互动需求激增的当下&#xff0c;无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作&#xff0c;还是游戏直播的画面实时传输&#xff0c;低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架&#xff0c;凭借其灵活的编解码、数据…...

编程新知 2025/11/4 6:26:59

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

Cinnamon修改面板小工具图标

Cinnamon开始菜单-CSDN博客 设置模块都是做好的&#xff0c;比GNOME简单得多&#xff01; 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

编程新知 2026/1/31 14:56:22

ardupilot 开发环境eclipse 中import 缺少C++

目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++，无法导入ardupilot代码，会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

编程新知 2026/1/31 5:06:34

代理篇12|深入理解 Vite中的Proxy接口代理配置

在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...

编程新知 2025/10/27 20:33:34

Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信

文章目录 Linux C语言网络编程详细入门教程&#xff1a;如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket&#xff08;服务端和客户端都要&#xff09;2. 绑定本地地址和端口&#x…...

编程新知 2025/10/31 21:54:15

RSS 2025｜从说明书学习复杂机器人操作任务：NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill

视觉语言模型&#xff08;Vision-Language Models, VLMs&#xff09;&#xff0c;为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展&#xff0c;机器人仍难以胜任复杂的长时程任务&#xff08;如家具装配&#xff09;&#xff0c;主要受限于人…...

编程新知 2026/1/31 5:30:51

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分&#xff1a; 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

编程新知 2025/8/27 0:09:05

CSS3相关知识点

CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

编程新知 2026/2/5 1:50:16

用 Rust 重写 Linux 内核模块实战：迈向安全内核的新篇章

用 Rust 重写 Linux 内核模块实战&#xff1a;迈向安全内核的新篇章 ​​摘要&#xff1a;​​ 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言&#xff0c;受限于 C 语言本身的内存安全和并发安全问题&#xff0c;开发复杂模块极易引入难以…...

编程新知 2025/10/25 19:31:21