【算法刷题day44】Leetcode:518. 零钱兑换 II、377. 组合总和 Ⅳ
文章目录
- Leetcode 518. 零钱兑换 II
- 解题思路
- 代码
- 总结
- Leetcode 377. 组合总和 Ⅳ
- 解题思路
- 代码
- 总结
草稿图网站
java的Deque
Leetcode 518. 零钱兑换 II
题目:518. 零钱兑换 II
解析:代码随想录解析
解题思路
先遍历物品,再遍历背包。
代码
class Solution {public int change(int amount, int[] coins) {int []dp = new int[amount+1];dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {dp[j] += dp[j - coins[i]];//加上这张钱外的钱的总数}}return dp[amount];}
}
总结
暂无
Leetcode 377. 组合总和 Ⅳ
题目:377. 组合总和 Ⅳ
解析:代码随想录解析
解题思路
先遍历背包,再遍历物品
代码
class Solution {public int combinationSum4(int[] nums, int target) {int []dp = new int[target+1];dp[0] = 1;for (int j = 0; j <= target; j++) {for (int i = 0; i < nums.length; i++) {if (j >= nums[i]) {dp[j] += dp[j-nums[i]];}}}return dp[target];}
}
总结
暂无
相关文章:

【算法刷题day44】Leetcode:518. 零钱兑换 II、377. 组合总和 Ⅳ
文章目录 Leetcode 518. 零钱兑换 II解题思路代码总结 Leetcode 377. 组合总和 Ⅳ解题思路代码总结 草稿图网站 java的Deque Leetcode 518. 零钱兑换 II 题目:518. 零钱兑换 II 解析:代码随想录解析 解题思路 先遍历物品,再遍历背包。 代码…...
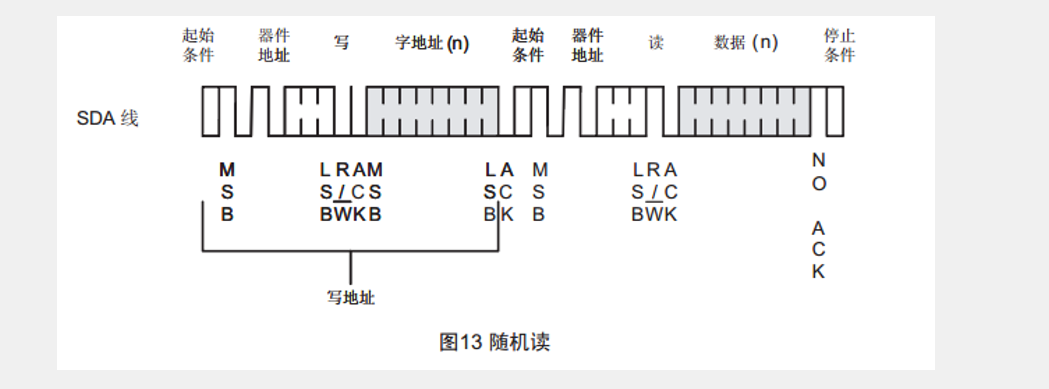
『51单片机』AT24C02[IIC总线]
存储器的介绍 ⒈ROM的功能⇢ROM的数据在程序运行的时候是不容改变的,除非你再次烧写程序,他就会改变,就像我们的书本,印上去就改不了了,除非再次印刷,这个就是ROM的原理。 注→在后面发展的ROM是可以可写可…...

Jenkins与Rancher的配合使用
Jenkins和Rancher是两个常用的DevOps工具,可以很好地配合使用来实现持续集成和持续部署。 Jenkins是一个开源的自动化构建工具,可以实现自动化的代码构建、测试和部署等一系列操作。可以通过Jenkins来触发构建任务,例如从代码仓库中拉取最新的…...

GIS入门,常用的多边形平滑曲线算法介绍和JavaScript的多边形平滑曲线算法库chaikin-smooth的实现原理和使用
前言 本章介绍一下常用的多边形平滑曲线算法及其使用案例。 多边形平滑算法通常用于图形处理或计算机图形学中,以使线条或曲线在连接处平滑过渡,而不出现明显的棱角或断裂。多边形平滑算法有多种实现方法,其中一些常见的有下面几种: 贝塞尔曲线插值(Bezier Curve Interpo…...

气膜体育馆内部的采光效果如何?—轻空间
气膜体育馆内部的采光效果如何?这是许多人对这种创新建筑的一个关键关注点。 首先,气膜体育馆的采光性非常好。阳光透过屋顶时以漫射光的方式进入室内,这种透射方式使得室内的光线柔和而均匀。从内部观察,整个屋顶就像一个连续的明…...
)
矩阵的对称正定性判决(复习)
文章目录 本科学的数学知识忘的太快了 如何判断一个实矩阵是否是对称正定 在线性代数中,一个实对称矩阵是否为正定可以通过以下方法判断: 对称性: 首先,确认矩阵是否对称,即矩阵的转置是否等于其本身。 特征值检查&…...
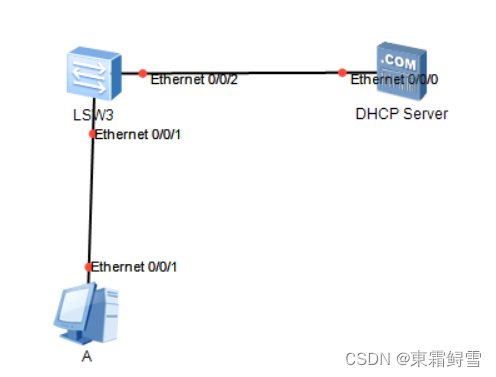
网络安全之DHCP详解
DHCP:Dynamic Host Configration Protocol 动态主机配置协议 某一协议的数据是基于UDP封装的,当它想确保自己的可靠性时,这个协议要么选确认重传机制,要么选周期性传输。 DHCP是确认重传,【UDP|DHCP】,当DHCP分配完地…...
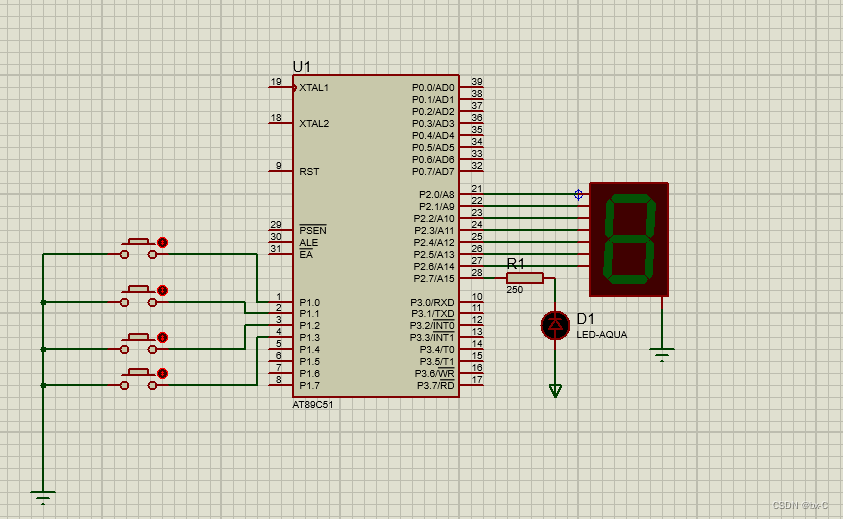
【Proteus】LED呼吸灯 直流电机调速
1.LED呼吸灯 #include <REGX51.H> sbit LEDP2^0; void delay(unsigned int t) {while(t--); } void main() {unsigned char time,i;while(1){for(time0;time<100;time){for(i0;i<20;i){LED0;delay(time);LED1;delay(100-time);}}for(time100;time>0;time--){fo…...
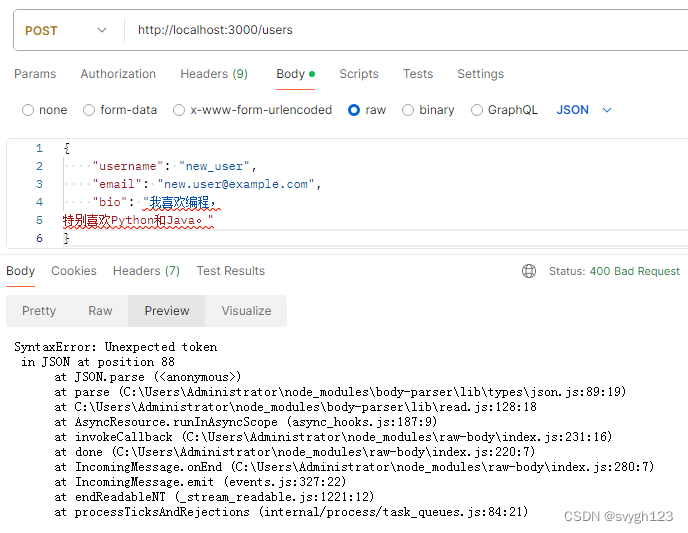
今天遇到一个GPT解决不了的问题
问题描述 你好,postman的一个post请求,编辑器里面放了一个很长的json数据,报Tokenization is skipped for long lines for performance reasons. This can be configured via editor.maxTokenizationLineLength.,但是同样的数据&a…...

优化SQL的方法
来自组内分享,包含了比较常使用到的八点: 避免使用select * union all代替union 小表驱动大表 批量操作 善用limit 高效的分页 用连接查询代替子查询 控制索引数量 一、避免使用select * 消耗数据库资源 消耗更多的数据库服务器内存、CPU等资源。 消…...

库存管理系统开源啦
软件介绍 ModernWMS是一个针对小型物流仓储供应链流程的开源库存管理系统。该系统的开发初衷是为了满足中小型企业在有限IT预算下对仓储管理的需求。通过总结多年ERP系统研发经验,项目团队开发了这套适用于中小型企业的系统,以帮助那些有特定需求的用户。…...
【java】接口
什么是接口 接口当中存在的是对方法的定义,而不是对方法的具体实现。 为什么不实现这个方法呢? 继承的本质是代码的复用。当一个父类会经常被继承,并且子类都要自己实现方法时,父类中的方法就会显得累赘,并且占用了…...

Java中的类型转换
一、类型转换 对类型转换来说分为向上类型转换和向下类型转换: 向上类型转换是自动完成的,一般是小类型向大类型转换。在引用类型中是子类型向父类型转换。向下类型转换是强制完成的,一般是大类型向小类型转换。在引用类型中是父类型向子类…...

定义范围对PFMEA分析的重要性——SunFMEA软件
在进行PFMEA分析时,定义范围是一个至关重要的步骤。这是因为,通过明确分析的范围,可以确保团队关注到最关键、最可能影响产品质量的过程,从而更有效地识别和解决潜在问题。今天SunFMEA软件和大家一起讨论定义范围对PFMEA操作的重要…...

json返回工具类|世界协调时间(UTC)
一、问题 世界协调时间(UTC)是一个标准的时间参考,通常被用于跨越不同时区的时间标准。要将 UTC 时间转换为中国时间(中国标准时间),你需要将时间加上8个小时,因为中国位于 UTC8 时区。 初中知…...
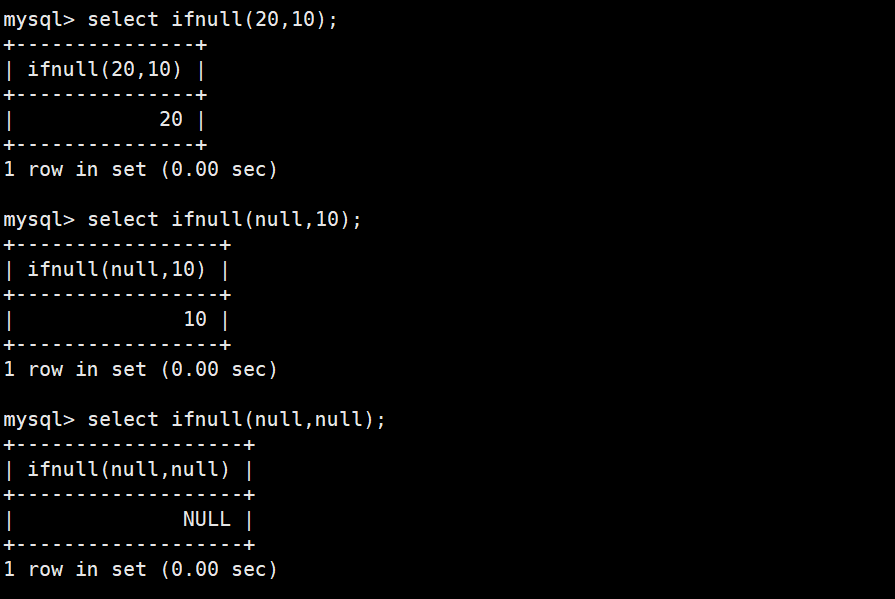
MySQL·内置函数
目录 函数 日期函数 案例1:创建一张表,记录生日 案例2:创建一个留言表 案例3:请查询在2分钟内发布的帖子 字符串函数 案例1: 获取emp表的ename列的字符集 案例2:要求显示exam_result表中的信息&am…...

vue根据文字动态判断溢出...鼠标悬停显示el-tooltip展示
使用自定义el- tooltip 组件 定义 Tooltip是一种小型弹出框,它显示有关特定页面元素的信息,例如按钮、链接或图标。Tooltip通常以半透明的气泡形式呈现,并出现在页面元素的旁边或下方。 它可以改善用户体验,使用户更容易理解页面元素的功能和意图。用户可以通过将鼠标悬停…...
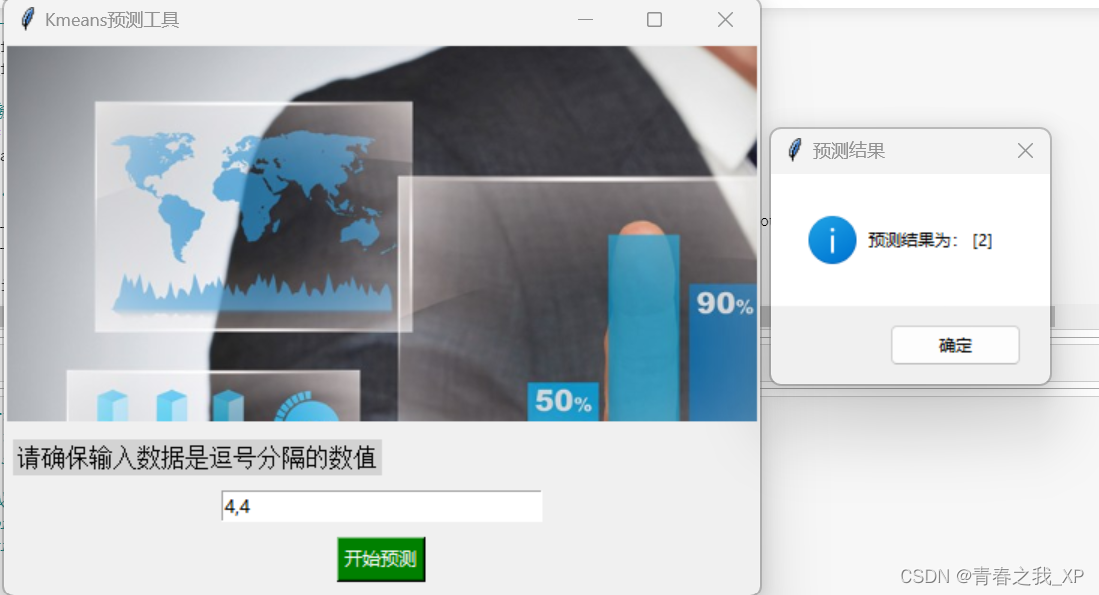
使用Tkinter实现数据预测工具的GUI界面展示
如果构建好预测模型后,想将预测模型通过一个交互式的页面显示,可以通过下边两种方式实现。 本文中代码有详细解析注释,便不再如往期一样分开讲解了,有需要的朋友可以直接拿去使用,代码可以直接运行,把预测…...

机器学习笔记-22
终章 至此吴恩达老师的机器学习课程已经完成啦,总结一下: 1.监督学习的算法:线性回归、逻辑回归、神经网络和向量机 2.无监督学习的算法:K-Means、PCA、异常检测 3.推荐系统、大规模数据处理、正则化、如何评估算法 4.上限分析、…...

车间为什么选择蒸发式冷风机?
蒸发式冷风机具有以下特点: 节能环保:蒸发式冷风机不使用压缩机和化学制冷剂,而是通过水的蒸发来降低温度,因此它是无压缩机、无冷媒、无污染的环保型产品。降温效果显著:在较潮湿地区,它一般能达到5-9℃的…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
