C# 局部静态函数,封闭方法中的最佳选择
C# 局部静态函数,封闭方法中的最佳选择
- 简介
- 特性
- 应用场景
- 辅助计算
- 递归与尾递归优化
- 筛选与过滤操作
- 查找与映射操作
- 生命周期
- 静态局部函数 vs 普通局部函数
- 性能
- 封装性
- 可读性
简介
C# 局部静态函数(Local Static Functions)是一种函数作用域内的嵌套函数,同时可以标记为 static,在 C# 8.0 中引入。这种特性允许我们定义更安全、更高效、更可读的辅助方法,并能在某些业务场景下带来便利和性能优化。
- 局部函数:在另一个函数内定义的嵌套函数,具有访问外部作用域变量的能力。
- 静态局部函数:添加 static 关键字,使得局部函数无法访问外部作用域变量。
using System;class Program
{static void Main(){// 局部变量int outerVariable = 42;// 普通局部函数,可以访问外部变量int NormalLocalFunction(){return outerVariable + 10;}// 静态局部函数,无法访问外部变量static int StaticLocalFunction(){return 10; // outerVariable 不可见}Console.WriteLine(NormalLocalFunction()); // 输出:52Console.WriteLine(StaticLocalFunction()); // 输出:10}
}
特性
- 封装性:局部函数属于封闭函数的内部实现细节,提高封装性。
- 静态性:静态局部函数不依赖外部变量,避免潜在的闭包问题,性能更好。
- 作用域:局部函数在封闭函数的作用域内定义和使用。
应用场景
辅助计算
可以将静态局部函数用于计算或转换操作,避免重复计算,提高代码可读性。
using System;class Program
{static void Main(){double CalculateCircleArea(double radius){static double Square(double x) => x * x;const double Pi = 3.141592653589793;return Pi * Square(radius);}double area = CalculateCircleArea(10);Console.WriteLine($"Area of circle: {area}");}
}
将局部函数声明为 static 会避免捕获外部变量,从而防止编译器生成闭包对象,提高性能。
递归与尾递归优化
静态局部函数非常适合用于递归计算。通过局部函数实现尾递归[^1] 优化。
using System;class Program
{static void Main(){int Factorial(int n){static int InnerFactorial(int n, int acc){if (n <= 1) return acc;return InnerFactorial(n - 1, acc * n);}return InnerFactorial(n, 1);}Console.WriteLine($"Factorial of 5: {Factorial(5)}"); // 输出:120}
}
[^1] 递归调用作为最后操作,累积结果直接传递,优化了栈深度
筛选与过滤操作
静态局部函数可以用于复杂的筛选和过滤操作,提高代码复用性和可读性。
using System;
using System.Collections.Generic;
using System.Linq;class Program
{static void Main(){IEnumerable<int> FilterNumbers(IEnumerable<int> numbers){static bool IsEven(int number) => number % 2 == 0;return numbers.Where(IsEven);}var numbers = new[] { 1, 2, 3, 4, 5, 6 };var evenNumbers = FilterNumbers(numbers);Console.WriteLine("Even numbers:");foreach (var number in evenNumbers){Console.WriteLine(number);}}
}
查找与映射操作
静态局部函数可以用于查找、映射等操作,将复杂逻辑封装在局部函数内。
using System;
using System.Collections.Generic;class Program
{static void Main(){string GetGrade(int score){static string MapScoreToGrade(int score) => score switch{>= 90 => "A",>= 80 => "B",>= 70 => "C",>= 60 => "D",_ => "F"};return MapScoreToGrade(score);}var scores = new Dictionary<string, int>{{ "Alice", 92 },{ "Bob", 83 },{ "Charlie", 78 },{ "Dave", 55 }};foreach (var (name, score) in scores){Console.WriteLine($"{name}: {GetGrade(score)}");}}
}
生命周期
- 局部静态函数属于封闭函数内部。
- 封闭函数调用时,局部静态函数随之被定义,并作为封闭函数的一部分进行编译。
- 局部静态函数在封闭函数调用期间会被实例化并执行。它的生命周期与封闭函数的执行周期相关。
静态局部函数 vs 普通局部函数
性能
- 静态局部函数不捕获外部变量,不产生闭包对象,因此性能更优。
封装性
- 静态局部函数无法访问外部变量,更具封装性,减少意外副作用。
可读性
- 静态局部函数能明确表明不依赖外部状态,提高代码的可读性和逻辑清晰度。
提示:如果需要在封闭的方法内定义一个方法,并且这个方法只在封闭的方法内使用,那么使用局部静态函数通常是最佳选择。
相关文章:

C# 局部静态函数,封闭方法中的最佳选择
C# 局部静态函数,封闭方法中的最佳选择 简介特性 应用场景辅助计算递归与尾递归优化筛选与过滤操作查找与映射操作 生命周期静态局部函数 vs 普通局部函数性能封装性可读性 简介 C# 局部静态函数(Local Static Functions)是一种函数作用域内…...
安装)
【MySQL】MySQL 8.4.0 长期支持版(LTS)安装
就在2024年 “5.1” 节前,MySQL官方发布了8.4.0长期支持版(LTS - Long Term Support)。根据官方提供的文档,在本地虚拟机进行安装测试。 安装、配置和启动过程记录如下: 第一步,上传到安装包(my…...

nest中的ORM
在 Nest.js 中执行 SQL 查询通常涉及使用 TypeORM 或 Sequelize 这样的 ORM(对象-关系映射)库。这些库使得在 Nest.js 应用程序中连接和操作 SQL 数据库变得更加简单和直观。 以下是一个使用 TypeORM 在 Nest.js 中执行 SQL 查询的示例代码:…...
如何保证数据的完整性?)
TCP(Transmission Control Protocol,传输控制协议)如何保证数据的完整性?
TCP(Transmission Control Protocol,传输控制协议)通过一系列机制来保证数据传输的可靠性和无错性,这些机制主要包括: 校验和:TCP报文段包含一个校验和字段,用于检测数据在传输过程中是否出错。…...

Numpy库介绍
NumPy(Numerical Python的缩写)是Python中用于科学计算的一个强大的库。它提供了高性能的多维数组对象(即ndarray)、用于处理这些数组的工具以及用于数学函数操作的函数。让我为你介绍一下它的一些主要功能: 1. 多维数…...
临时有事无法及时签字盖章?试试用契约锁设置“代理人”
遇到“领导休假中、在开重要会议、外出考察或者主任医生手术中等”一段时间内不方便或者无法及时签字盖章的情况怎么办?业务推进不了只能干等? 契约锁电子签及印控平台支持印章、签名“临时授权”、“代理签署”,实现指定人、指定时间段、指定…...

数据库权限管理
1.查看系统级权限(global level) Select * from mysql.user\G; 2.查看数据库中所有表的权限 Select * from mysql.db\G 3.远程连接数据库 第一步在有数据库服务上的主机上:授权 grant all on *.* to root192.168.40.83 identified by Zxy20234; 第…...

如何创建一个 Django 应用并连接到数据库
简介 Django 是一个用 Python 编写的免费开源的 Web 框架。这个工具支持可扩展性、可重用性和快速开发。 在本教程中,您将学习如何为一个博客网站建立与 MySQL 数据库的初始基础。这将涉及使用 django-admin 创建博客 Web 应用程序的骨架结构,创建 MyS…...

【算法刷题day44】Leetcode:518. 零钱兑换 II、377. 组合总和 Ⅳ
文章目录 Leetcode 518. 零钱兑换 II解题思路代码总结 Leetcode 377. 组合总和 Ⅳ解题思路代码总结 草稿图网站 java的Deque Leetcode 518. 零钱兑换 II 题目:518. 零钱兑换 II 解析:代码随想录解析 解题思路 先遍历物品,再遍历背包。 代码…...
『51单片机』AT24C02[IIC总线]
存储器的介绍 ⒈ROM的功能⇢ROM的数据在程序运行的时候是不容改变的,除非你再次烧写程序,他就会改变,就像我们的书本,印上去就改不了了,除非再次印刷,这个就是ROM的原理。 注→在后面发展的ROM是可以可写可…...

Jenkins与Rancher的配合使用
Jenkins和Rancher是两个常用的DevOps工具,可以很好地配合使用来实现持续集成和持续部署。 Jenkins是一个开源的自动化构建工具,可以实现自动化的代码构建、测试和部署等一系列操作。可以通过Jenkins来触发构建任务,例如从代码仓库中拉取最新的…...

GIS入门,常用的多边形平滑曲线算法介绍和JavaScript的多边形平滑曲线算法库chaikin-smooth的实现原理和使用
前言 本章介绍一下常用的多边形平滑曲线算法及其使用案例。 多边形平滑算法通常用于图形处理或计算机图形学中,以使线条或曲线在连接处平滑过渡,而不出现明显的棱角或断裂。多边形平滑算法有多种实现方法,其中一些常见的有下面几种: 贝塞尔曲线插值(Bezier Curve Interpo…...

气膜体育馆内部的采光效果如何?—轻空间
气膜体育馆内部的采光效果如何?这是许多人对这种创新建筑的一个关键关注点。 首先,气膜体育馆的采光性非常好。阳光透过屋顶时以漫射光的方式进入室内,这种透射方式使得室内的光线柔和而均匀。从内部观察,整个屋顶就像一个连续的明…...
)
矩阵的对称正定性判决(复习)
文章目录 本科学的数学知识忘的太快了 如何判断一个实矩阵是否是对称正定 在线性代数中,一个实对称矩阵是否为正定可以通过以下方法判断: 对称性: 首先,确认矩阵是否对称,即矩阵的转置是否等于其本身。 特征值检查&…...
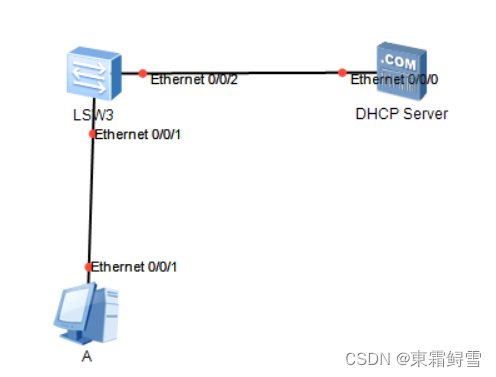
网络安全之DHCP详解
DHCP:Dynamic Host Configration Protocol 动态主机配置协议 某一协议的数据是基于UDP封装的,当它想确保自己的可靠性时,这个协议要么选确认重传机制,要么选周期性传输。 DHCP是确认重传,【UDP|DHCP】,当DHCP分配完地…...
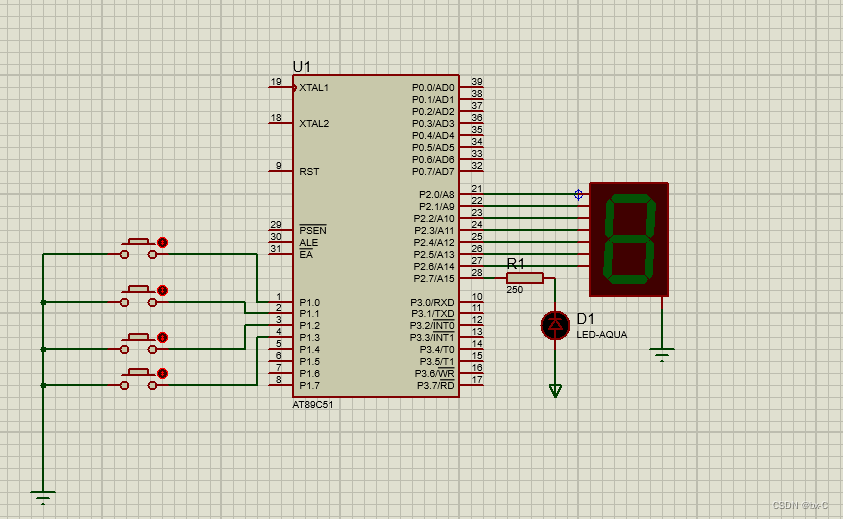
【Proteus】LED呼吸灯 直流电机调速
1.LED呼吸灯 #include <REGX51.H> sbit LEDP2^0; void delay(unsigned int t) {while(t--); } void main() {unsigned char time,i;while(1){for(time0;time<100;time){for(i0;i<20;i){LED0;delay(time);LED1;delay(100-time);}}for(time100;time>0;time--){fo…...
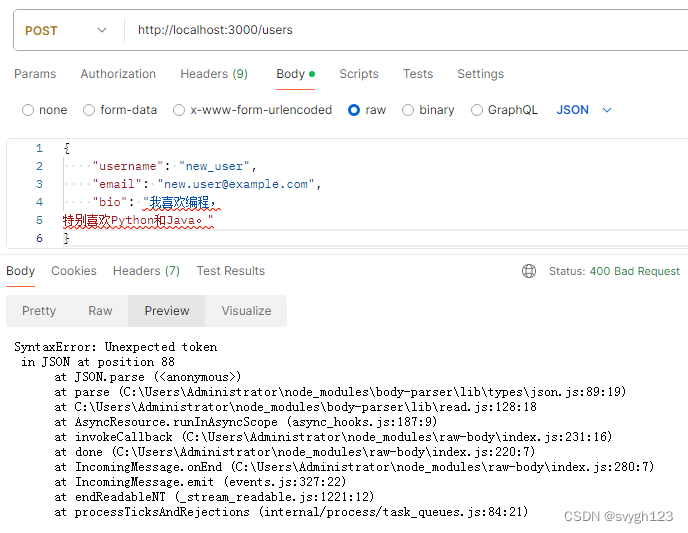
今天遇到一个GPT解决不了的问题
问题描述 你好,postman的一个post请求,编辑器里面放了一个很长的json数据,报Tokenization is skipped for long lines for performance reasons. This can be configured via editor.maxTokenizationLineLength.,但是同样的数据&a…...

优化SQL的方法
来自组内分享,包含了比较常使用到的八点: 避免使用select * union all代替union 小表驱动大表 批量操作 善用limit 高效的分页 用连接查询代替子查询 控制索引数量 一、避免使用select * 消耗数据库资源 消耗更多的数据库服务器内存、CPU等资源。 消…...

库存管理系统开源啦
软件介绍 ModernWMS是一个针对小型物流仓储供应链流程的开源库存管理系统。该系统的开发初衷是为了满足中小型企业在有限IT预算下对仓储管理的需求。通过总结多年ERP系统研发经验,项目团队开发了这套适用于中小型企业的系统,以帮助那些有特定需求的用户。…...
【java】接口
什么是接口 接口当中存在的是对方法的定义,而不是对方法的具体实现。 为什么不实现这个方法呢? 继承的本质是代码的复用。当一个父类会经常被继承,并且子类都要自己实现方法时,父类中的方法就会显得累赘,并且占用了…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
