大语言模型从Scaling Laws到MoE
1、摩尔定律和伸缩法则
摩尔定律(Moore's law)是由英特尔(Intel)创始人之一戈登·摩尔提出的。其内容为:集成电路上可容纳的晶体管数目,约每隔两年便会增加一倍;而经常被引用的“18个月”,则是由英特尔首席执行官大卫·豪斯(David House)提出:预计18个月会将芯片的性能提高一倍(即更多的晶体管使其更快),是一种以倍数增长的观测。[1]

然而,由于受到晶体管的散热问题、内存带宽瓶劲等问题,摩尔定律目前已经走到了物理的极限,限制了我们做出更快的芯片。
另一方面,OpenAI提出了Scaling Laws[2],其中列举了影响模型性能最大的三个因素:计算量、数据集大小、模型参数量。也就是说,当其他因素不成为瓶颈时,计算量、数据集大小、模型参数量这3个因素中的单个因素指数增加时,loss会线性的下降。同时,DeepMind的研究也得出来和OpenAI类似的结论[3]。

Scaling Laws for Neural Language Models
根据Scaling Laws,模型越大、数据量越大、计算量越大,模型效果也越好。因此,目前很多LLM都是朝着更多参数、更多训练数据的方向进行scaling。然而,随着摩尔定律走到了尽头,LLM也不可能做到无限大。那么计算受到限制的时候,该如何进一步提升模型的性能呢?其中一种方法是MoE。
2、使用MoE进行LLM的scaling
MoE(the mixture of experts model)的思想是训练多个神经网络(也就是多个experts),每个神经网络 (expert) 被指定 (specialize) 应用于数据集的不同部分。对于不同来源的数据,有一个managing neural net来判断应该交给哪一个 expert 进行处理。
2.1 GLaM
2022年,Google发布了MoE的模型GLaM[4]。GLaM是一个 decoder only 模型,支持 in-context learning,一共有1.2T的参数量,其中有97B是激活的。

GLaM: Efficient Scaling of Language Models with Mixture-of-Experts
GLaM在训练和推理时所需的计算量,都远低于GPT3。同时,在zero-shot、one-shot 和 few shot 方面,GLaM的效果都优于GPT3。
2.2 Expert Choice Routing
GLaM 虽然效果不错,但是有负载不均衡问题。也就是说,会有一部分 expert 会经常被激活,而有一些 expert 很少被激活。
2022年,在 NeurIPS上,提出了新的 Expert Choice Routing 方法[5],来解决负载不均衡问题。该方法中,每个expert 会独立选择 top-k 的tokens 作为输入。每个token都可能会被不同的 expert 选择。一些比较重要的tokens会得到更多的计算资源,而不重要的 tokens 得到的计算资源会比较少。

Mixture-of-Experts with Expert Choice Routing
采用 Expert Choice Routing 的模型,相比于GLaM,在收敛速度方面可以提升2倍, 在 step time 上提速20%,并且完美解决了负载不均衡问题。8B/64E 的模型(有9.8B激活的参数),在 SuperGLUE 上效果超过了 T5-11B 的模型。
3、MoE进阶技术
3.1 Brainformers
上述MoE模型,在训练速度很慢,会成为进一步 scaling 的瓶颈。在 ICML 2023上,进一步提出了Brainformers[6]。

Brainformers: Trading Simplicity for Efficiency
为了模型计算更快,需要对矩阵乘法进行分解,从而减少计算量。同时,这些矩阵分解,必须不能损害模型的准确性。上图 (a) 中,是两种分解矩阵乘法的主要方法,分别是从横向分解(low-rank)和纵向分解(multi-expert) 。而在图 (b)中,可以对 low-rank 和 multi-expert 进行组合、堆叠,以实现更有趣且计算效率高的模型架构。
如果在 bottleneck 处,插入一个 mixure 层,模型看起来就非常像 transformers。如果在 bottleneck 处,插入一个 attention layer,模型看起来就非常像一个 multi-expert transformers。
作者对不同的参数,进行了搜索,从而找到了最优的网络模型结果。搜索的空间包括:不同的层类型(attn、moe、ffn)、隐层维度、MoE隐层维度、FFN隐层维度、attention 的 head 数、Gating Fuction、Capacity Factor、Activation Function等。
从搜索空间中,采样一组参数,构建一个 100M/32E 的模型,选择top-K的模型,然后进行scaling,如1B/64E 、8B/64E。

Brainformers: Trading Simplicity for Efficiency
相比于GLaM,可以在收敛速度方面,提速2倍;在 step time 上提速5倍。
3.2 Lifelong Language Pretraining
其他问题:如何进行增量训练,同时避免灾难性遗忘。
方法:引入新的数据分布时,引入新的 experts,同时冻结原有的权重,并且加入一个regularization loss 避免灾难性遗忘[7]。

Lifelong Language Pretraining with Distribution-Specialized Experts
相比于baseline,Lifelong-MoE 的灾难性遗忘被显著抑制,并且比 dense oracle 的效果还要好。
4、问答及彩蛋
- MoE model 的训练,有2种方案,一种是 train from scratch,一种是 dense to sparse
- GPT4是一个MoE model,且大概率是一个 train from scratch 的 MoE model
- 如果 finetune 后的 MoE 效果变差,可能是 finetune 没有训好,需要增加新的 experts
- Google 从 NVIDIA 买了 26,000 个 H100 (真有钱)
- H100 针对 transformers 训练做了专门的优化,主要是卡与卡之间的通讯优化,比 A100 提速 10倍左右
参考
- 摩尔定律-维基百科 https://zh.wikipedia.org/zh-hans/%E6%91%A9%E5%B0%94%E5%AE%9A%E5%BE%8B
- Scaling Laws for Neural Language Models https://arxiv.org/abs/2001.08361
- Training Compute-Optimal Large Language Models https://arxiv.org/abs/2203.15556
- GLaM: Efficient Scaling of Language Models with Mixture-of-Experts https://arxiv.org/abs/2112.06905
- Mixture-of-Experts with Expert Choice Routing https://arxiv.org/abs/2202.09368
- Brainformers: Trading Simplicity for Efficiency https://arxiv.org/abs/2306.00008
- Lifelong Language Pretraining with Distribution-Specialized Experts https://arxiv.org/abs/2305.12281
相关文章:

大语言模型从Scaling Laws到MoE
1、摩尔定律和伸缩法则 摩尔定律(Moores law)是由英特尔(Intel)创始人之一戈登摩尔提出的。其内容为:集成电路上可容纳的晶体管数目,约每隔两年便会增加一倍;而经常被引用的“18个月”…...

四级英语翻译随堂笔记
降维表达:中译英,英译英 没有强调主语,没有说明主语:用被动 但如果实在不行,再增添主语 不会就不翻译,不要乱翻译 以xxx为背景:against the backdrop of the xxx eg:against the backdrop of…...

Nacos支持的配置格式及其在微服务架构中的应用
今天,我想和大家探讨一下Nacos这一重要的微服务组件,特别是它所支持的配置格式以及这些格式在微服务架构中的应用。 一、Nacos简介 Nacos是阿里巴巴开源的一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。它提供了服务发现、配置管理…...
-OD统一考试(C卷D卷))
2024年华为OD机试真题-小明找位置-(C++)-OD统一考试(C卷D卷)
题目描述: 小朋友出操,按学号从小到大排成一列;小明来迟了,请你给小明出个主意,让他尽快找到他应该排的位置。 算法复杂度要求不高于nLog(n);学号为整数类型,队列规模<=10000; 输入描述: 1、第一行:输入已排成队列的小朋友的学号(正整数),以”,”隔开; …...
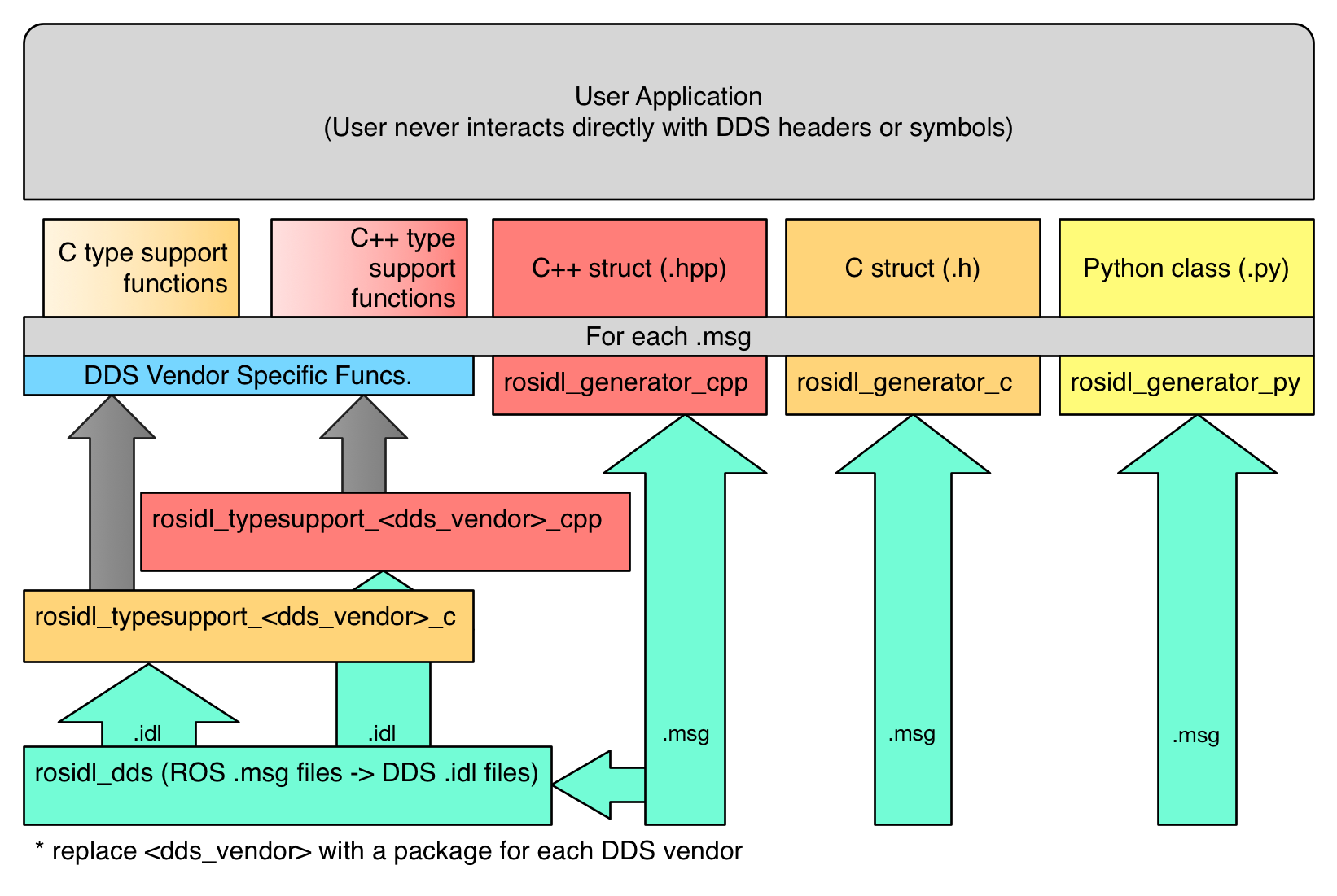
机器人系统ros2内部接口介绍
内部 ROS 接口是公共 C API ,供创建客户端库或添加新的底层中间件的开发人员使用,但不适合典型 ROS 用户使用。 ROS客户端库提供大多数 ROS 用户熟悉的面向用户的API,并且可能采用多种编程语言。 内部API架构概述 内部接口主要有两个&#x…...

跟随Facebook的足迹:社交媒体背后的探索之旅
在当今数字化时代,社交媒体已经成为了人们日常生活中不可或缺的一部分。而在这庞大的社交媒体网络中,Facebook作为其中的巨头,一直在引领着潮流。从创立之初的一个大学社交网络到如今的全球性平台,Facebook的发展历程承载了无数故…...

面试题分享之Java并发篇
注意:文章若有错误的地方,欢迎评论区里面指正 🍭 系列文章目录 面试题分享之Java集合篇(三) 面试题分享之Java集合篇(二) 面试题分享之Java基础篇(三) 前言 今天给小…...

bpmn-js 多实例配置MultiInstanceLoopCharacteristics实现或签会签
使用bpmn-js流程图开发过程中会遇到会签和或签的问题,这个时候我们就需要使用多实例配置来实现BPMN 2.0的配置实现了,多实例任务,是从流程编辑概念之初也就是Activiti时期就存在的一个方式。所谓的多实例任务也就是字面意思,一个任务由多个人完成,常见于我们的审批流程的或…...
【gpedit.msc】组策略编辑器的安装,针对windows家庭版,没有此功能
创建一个记事本文件然后放入以下内容 echo offpushd "%~dp0"dir /b %systemroot%\Windows\servicing\Packages\Microsoft-Windows-GroupPolicy-ClientExtensions-Package~3*.mum >gp.txtdir /b %systemroot%\servicing\Packages\Microsoft-Windows-GroupPolicy-…...
带EXCEL附件邮件发送相关代码
1.查看生成的邮件 2.1 非面向对象的方式(demo直接copy即可) REPORT Z12. DATA: IT_DOCUMENT_DATA TYPE SODOCCHGI1,IT_CONTENT_TEXT TYPE STANDARD TABLE OF SOLISTI1 WITH HEADER LINE,IT_PACKING_LIST TYPE TABLE OF SOPCKLSTI1 WITH HEADER LIN…...

【算法作业】均分卡牌,购买股票
问题描述 John 有两个孩子,在 John病逝后,留下了一组价值不一定相同的魔卡, 现在要求你设计一种策略,帮John的经管人将John的这些遗产分给他的两个孩子,使得他们获得的遗产差异最小(每张魔卡不能分拆&#…...
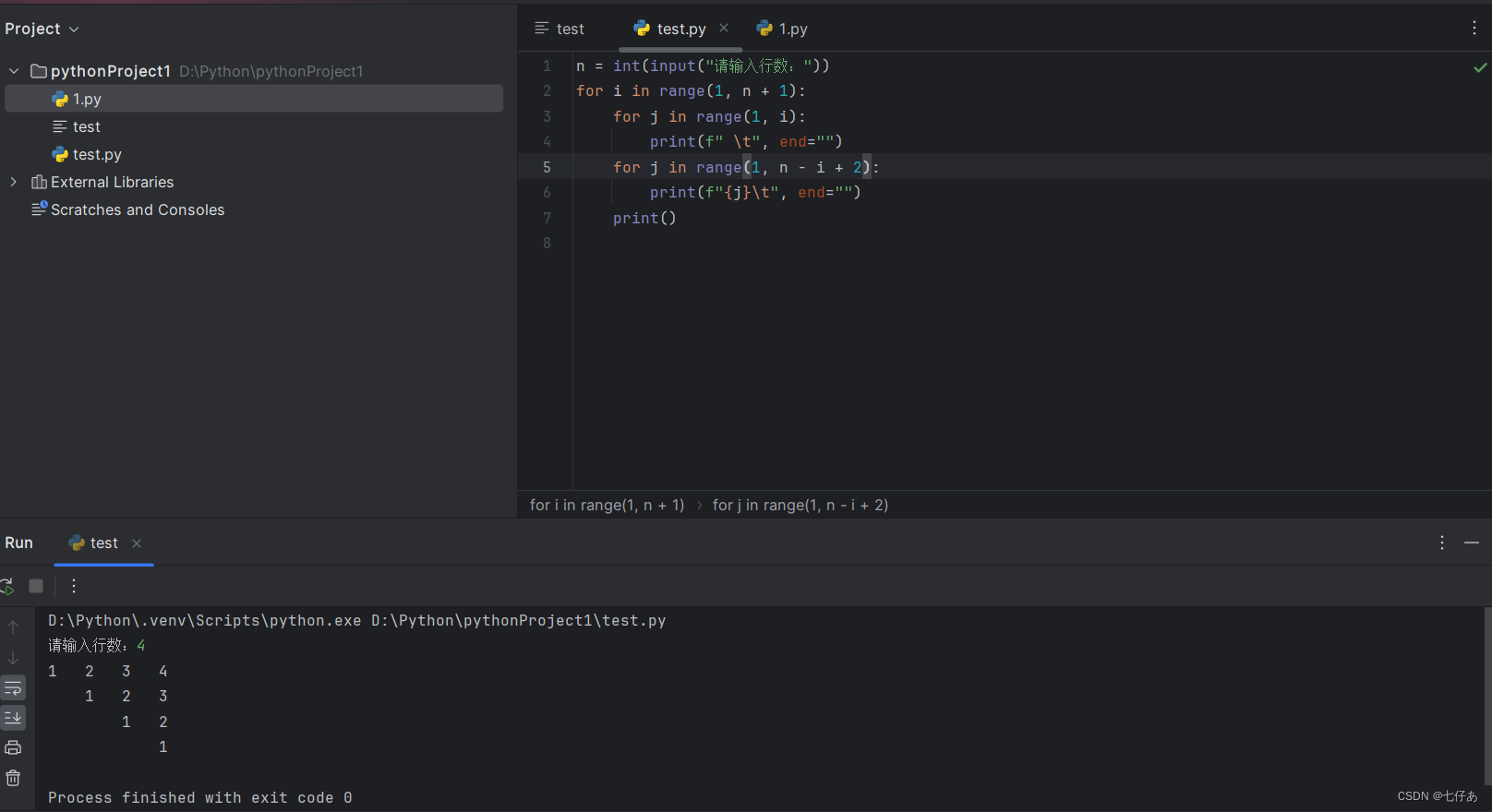
python作业
题目 分析 步骤: 判断先画空格还是数字 当有n层时,第i层有多少个空格第i层的起始数字是几,结尾是几,即数字取值范围当有n层时,第i层有多少个数字 代码 模式A n int(input("请输入行数:")) for i in range(…...

【Linux的文件篇章 - 管道文件】
Linux学习笔记---013 Linux的管道文件1、进程间通信1.1、进程为什么要通信?1.2、进程如何通信?1.3、进程通信的方式? 2、匿名管道2.1、理解一种现象2.2、基本概念和管道原理 3、管道的使用3.1、代码样例3.2、如何使用管道通信呢?3…...

C# 局部静态函数,封闭方法中的最佳选择
C# 局部静态函数,封闭方法中的最佳选择 简介特性 应用场景辅助计算递归与尾递归优化筛选与过滤操作查找与映射操作 生命周期静态局部函数 vs 普通局部函数性能封装性可读性 简介 C# 局部静态函数(Local Static Functions)是一种函数作用域内…...
安装)
【MySQL】MySQL 8.4.0 长期支持版(LTS)安装
就在2024年 “5.1” 节前,MySQL官方发布了8.4.0长期支持版(LTS - Long Term Support)。根据官方提供的文档,在本地虚拟机进行安装测试。 安装、配置和启动过程记录如下: 第一步,上传到安装包(my…...

nest中的ORM
在 Nest.js 中执行 SQL 查询通常涉及使用 TypeORM 或 Sequelize 这样的 ORM(对象-关系映射)库。这些库使得在 Nest.js 应用程序中连接和操作 SQL 数据库变得更加简单和直观。 以下是一个使用 TypeORM 在 Nest.js 中执行 SQL 查询的示例代码:…...
如何保证数据的完整性?)
TCP(Transmission Control Protocol,传输控制协议)如何保证数据的完整性?
TCP(Transmission Control Protocol,传输控制协议)通过一系列机制来保证数据传输的可靠性和无错性,这些机制主要包括: 校验和:TCP报文段包含一个校验和字段,用于检测数据在传输过程中是否出错。…...

Numpy库介绍
NumPy(Numerical Python的缩写)是Python中用于科学计算的一个强大的库。它提供了高性能的多维数组对象(即ndarray)、用于处理这些数组的工具以及用于数学函数操作的函数。让我为你介绍一下它的一些主要功能: 1. 多维数…...
临时有事无法及时签字盖章?试试用契约锁设置“代理人”
遇到“领导休假中、在开重要会议、外出考察或者主任医生手术中等”一段时间内不方便或者无法及时签字盖章的情况怎么办?业务推进不了只能干等? 契约锁电子签及印控平台支持印章、签名“临时授权”、“代理签署”,实现指定人、指定时间段、指定…...

数据库权限管理
1.查看系统级权限(global level) Select * from mysql.user\G; 2.查看数据库中所有表的权限 Select * from mysql.db\G 3.远程连接数据库 第一步在有数据库服务上的主机上:授权 grant all on *.* to root192.168.40.83 identified by Zxy20234; 第…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
