Dive into Deep Learning-优化算法(1)
- 优化和深度学习的关系
- 优化是最小化损失函数,而深度学习的目标是在给定有限数据量的情况下寻找合适的模型,分别对应着训练误差和泛化误差;
- 需要注意过拟合;
- 优化面临的挑战(求解数值解)
- 局部最小值:当优化问题的数值解接近局部最优值的时候,目标函数解的梯度接近或者变为0,通过迭代获得的数值解可能仅使目标函数局部最优,而不是全局最优,一定程度的噪声会使参数跳出局部最小值,这是小批量随机梯度下降的有利特性之一,此时小批量上梯度的自然变化能够将参数从局部最小资中跳出;
- 鞍点:定义为梯度为0但是既不是全局最小值也不是局部最小值的点,尽管不是最小值,但是优化可能会停止,假设输入是k维向量,假设在0梯度处的Hessian矩阵的k个特征值均为正,此时局部最小值,均为负,为局部最大值,有正有负为鞍点;
- 梯度消失
- 凸性
- 凸集:对于任意的 a , b ∈ X a,b\in X a,b∈X,连接 a , b a,b a,b的线段也位于 X X X,则集合 X X X是凸集,数学化表示,对于任意 λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ∈[0,1],有 λ a + ( 1 − λ ) b ∈ X \lambda a + (1-\lambda) b\in X λa+(1−λ)b∈X,例如实数集,两个凸集的交集也是凸集;
- 凸函数:对于所有 x , x ′ ∈ X , λ ∈ [ 0 , 1 ] x,x'\in X,\lambda\in [0,1] x,x′∈X,λ∈[0,1],有 λ f ( x ) + ( 1 − λ ) f ( x ′ ) ≥ f ( λ x + ( 1 − λ ) x ′ ) \lambda f(x) + (1-\lambda)f(x') \geq f(\lambda x + (1-\lambda)x') λf(x)+(1−λ)f(x′)≥f(λx+(1−λ)x′);
- 詹森不等式:凸性定义的推广 ∑ i α i f ( x i ) ≥ f ( ∑ i α i x i ) , ∑ i α i = 1 \sum_i\alpha_if(x_i)\geq f(\sum_i\alpha_i x_i),\sum_i\alpha_i=1 ∑iαif(xi)≥f(∑iαixi),∑iαi=1;
- 凸函数的性质:凸函数的局部极小值是全局极小值
i. 特征值和特征向量, A v = λ v Av=\lambda v Av=λv,其中 v v v是特征向量, λ \lambda λ是特征值;例如对于 A = [ 2 1 2 3 ] A = \begin{bmatrix} 2 & 1\\ 2 & 3\end{bmatrix} A=[2213],他的特征值是 4 , 1 4,1 4,1对应的两个特征向量是 [ 1 2 ] \begin{bmatrix} 1\\ 2\end{bmatrix} [12]和 [ 1 − 1 ] \begin{bmatrix} 1 \\ -1\end{bmatrix} [1−1]
ii. 求解特征值和特征向量: ( A − λ I ) v = 0 (A-\lambda I)v = 0 (A−λI)v=0,所以 ( A − λ I ) (A-\lambda I) (A−λI)不可逆,也就是 d e t ( A − λ I ) = 0 det(A-\lambda I)= 0 det(A−λI)=0,即可解得特征值
iii. 延续上面的例子,特征向量组成的矩阵 W = [ 1 1 − 1 2 ] W=\begin{bmatrix}1 & 1\\-1 & 2\end{bmatrix} W=[1−112],特征值组成的矩阵 ∑ = [ 1 0 0 4 ] \sum=\begin{bmatrix}1 & 0\\0 & 4\end{bmatrix} ∑=[1004],可得 A W = W ∑ AW=W\sum AW=W∑,而且 W W W是可逆的,所以等式两边同乘 W − 1 W^{-1} W−1得到 A = W ∑ W − 1 A=W\sum W^{-1} A=W∑W−1
iv. 一些良好的性质: A n = W ∑ n W − 1 A^n = W\sum^n W^{-1} An=W∑nW−1,也就是对应一个矩阵的乘方进行特征值分解,只需要将特征值进行同样的n次方即可,此时n需要时正数;对于矩阵的求逆, A − 1 = W ∑ − 1 W − 1 A^{-1}=W\sum^{-1}W^{-1} A−1=W∑−1W−1,可以看到对矩阵的逆进行特征值分解,直接对特征值求逆即可;矩阵的行列式等于矩阵的特征值的乘积 d e t ( A ) = λ 1 ⋯ λ n det(A) = \lambda_1\cdots \lambda_n det(A)=λ1⋯λn;矩阵的秩等于非0特征值的个数;
v. https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/eigendecomposition.html
相关文章:
)
Dive into Deep Learning-优化算法(1)
优化和深度学习的关系 优化是最小化损失函数,而深度学习的目标是在给定有限数据量的情况下寻找合适的模型,分别对应着训练误差和泛化误差;需要注意过拟合; 优化面临的挑战(求解数值解) 局部最小值&#…...
Partisia Blockchain 生态首个zk跨链DEX现已上线
在5月1日,由Partisia Blockchain与zkCross创建合作推出的Partisia zkCrossDEX在Partisia Blockchain生态正式上线。Partisia zkCrossDEX是Partisia Blockchain上重要的互操作枢纽,其融合了zkCross的zk技术跨链互操作方案,并利用Partisia Bloc…...
.NET操作 Access (MSAccess)
注意:新项目推荐 Sqlite ,Access需要注意的东西太多了,比如OFFICE版本,是X86还是X64 连接字符串 ProviderMicrosoft.ACE.OleDB.15.0;Data Source"GetCurrentProjectPath"\\test.accdb//不同的office版本 连接字符串有…...

shell脚本,删除30天以前的日志,并将日志推送到nas,但运行出现/bin/bash^M。
删除30天以前的日志 将日志推送到nas中,然后删除pod中的日志 pod挂载到本地 运行出现/bin/bash^M 1、删除30天以前的日志: #! /bin/bash# 定义源日志目录 LOG_DIR/home/log/ # 删除日志 find $LOG_DIR -type f -name "*.log" -mtime 30 -exec…...

现身说法暑期三下乡社会实践团一个好的投稿方法胜似千军万马
作为一名在校大学生,去年夏天我有幸参与了学院组织的暑期大学生三下乡社会实践活动,这段经历不仅让我深入基层,体验了不一样的生活,更是在新闻投稿的实践中,经历了一次从传统到智能的跨越。回忆起那段时光,从最初的邮箱投稿困境,到后来智慧软文发布系统的高效运用,每一步都刻印…...
小程序账号设置以及request请求的封装
一般开发在小程序时,都会有测试版和正式版,这样在开发时会比较方便。 在开发时。产品经理都会给到测试账号和正式账号,后端给的接口也都会有测试环境用到的接口和正式环境用到的接口。 这里讲一讲我这边如何去做的。 1.在更目录随便命名一…...

怎么解决端口被占用
目录 一、引言 二、解决方法 一、引言 最近用vscode写网页,老是遇见端口被占用,报错如下: listen tcp :8080: bind: Only one usage of each socket address (protocol/network address/port) is normally permitted. 二、解决方法 1.换…...

JavaScript 循环方法详解
在编程中,循环是一种重复执行代码块的机制,直到满足某个条件为止。JavaScript 提供了多种循环结构来帮助我们实现这一功能。以下是 JavaScript 中常用的几种循环方法的详细解释。 1. for 循环 for 循环是 JavaScript 中最常用的循环结构之一。它使用一…...
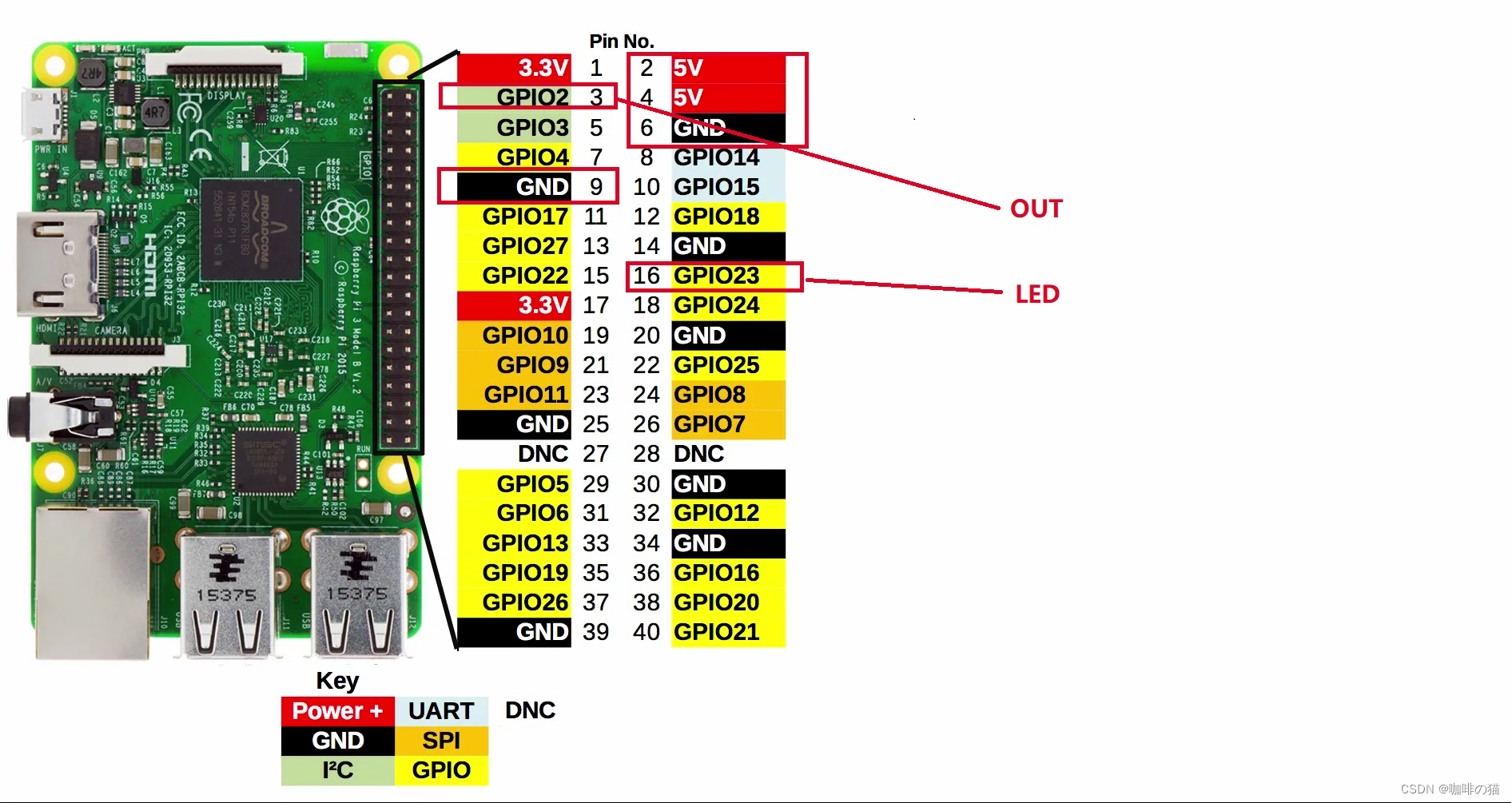
树莓派4b测量PM2.5
1.GP2Y1010AU0F粉尘传感器连接图 2. GP2Y1010AU0F工作原理 工作原理 传感器中心有个洞可以让空气自由流过,定向发射LED光,通过检测经过空气中灰尘折射过后的光线来判断灰尘的含量。 3.源代码 main.py # coding=UTF-8 import RPi.GPIO as GPIO from ADC import ADS1015…...

恒生电子,快手25届实习内推
恒生电子,快手25届实习内推 ①快手 【岗位】算法、工程、游戏,产品运营、市场、职能等 【一键内推】https://campus.kuaishou.cn/recruit/campus/e/h5/#/campus/jobs?codecampuswQrLOMvHE 【内推码】campuswQrLOMvHE ②恒生电子 【招聘岗位】JAVA、测试…...

蓝桥杯练习系统(算法训练)ALGO-949 勇士和地雷阵
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 勇士们不小心进入了敌人的地雷阵(用n行n列的矩阵表示,*表示某个位置埋有地雷,-表示某个…...
一面)
腾讯安全客户端(电脑管家部门)一面
上来介绍部门,之后自我介绍 说了是个喜欢每天都学点新东西的人,然后平常也会在课余时间之外去做点项目方面的学习,比如Web项目做出来就是因为兴趣。喜欢结构性的东西,有一门课叫电路电子学一次考试是专业第二。其他也都还可以&am…...

激励与关怀并行:员工工作动力倍增之道
在现代企业中,员工是推动公司发展的核心力量。如何激发员工的工作动力,使他们在工作中发挥出最大的潜力,一直是企业管理者关注的焦点。实际上,激励与关怀并行的策略,是一种非常有效的提升员工工作动力的方法。 激励是激…...

软件系统安全设计规范(word原件)
1.1安全建设原则 1.2 安全管理体系 1.3 安全管理规范 1.4 数据安全保障措施 1.4.1 数据库安全保障 1.4.2 操作系统安全保障 1.4.3 病毒防治 1.5安全保障措施 1.5.1实名认证保障 1.5.2 接口安全保障 1.5.3 加密传输保障 1.5.4终端安全保障 软件资料清单列表部分文档…...
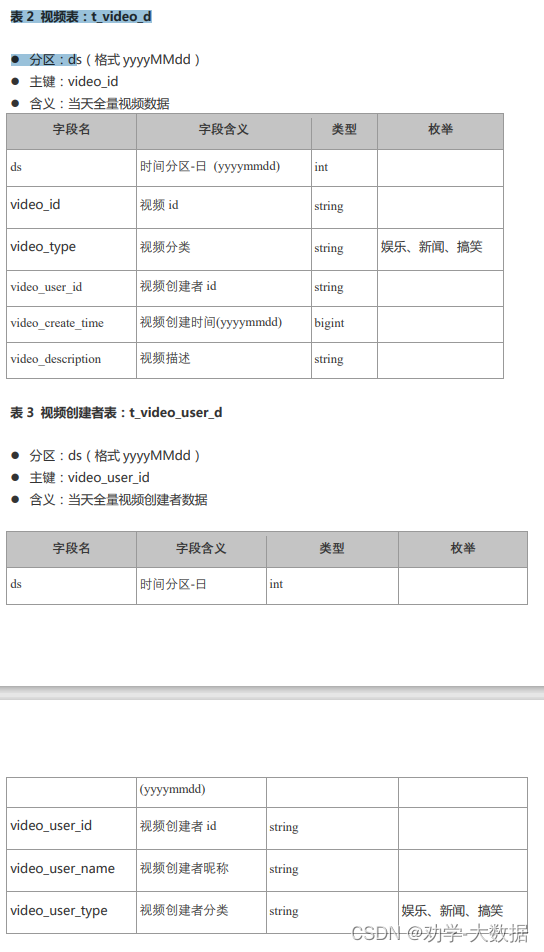
做题速度太慢了,面不上
没办法,之前练了一个月的sql。两个月不写,现在差不多忘干净了。工作空窗期,或者休息期不能太久,不然学再多的内容都可能会忘完的。 sql题,腾讯四道sql题,限时45分钟完成。我只做了一道,还没做完…...
Vue 路由
单应用程序 SPA - Single Page Application 所有功能在一个html页面上实现 单页面应用 多用于 系统类网站/内部网站/文档类网站/移动端站点 多页面应用 多用于 公司官网/电商类网站 路由 单页面应用按需更新页面,需要明确访问路径和组件的对应关系 Vue中的路…...

docker-compose-itd和d
docker run -itd和-d的区别 前言: 今天在通过docker-compose启动一基于ubuntu的镜像容器时,发现启动后,容器会一直停止。但是通过docker run -itd是可以正常运行的。基于这个区别,找了一位大神(师傅)问…...
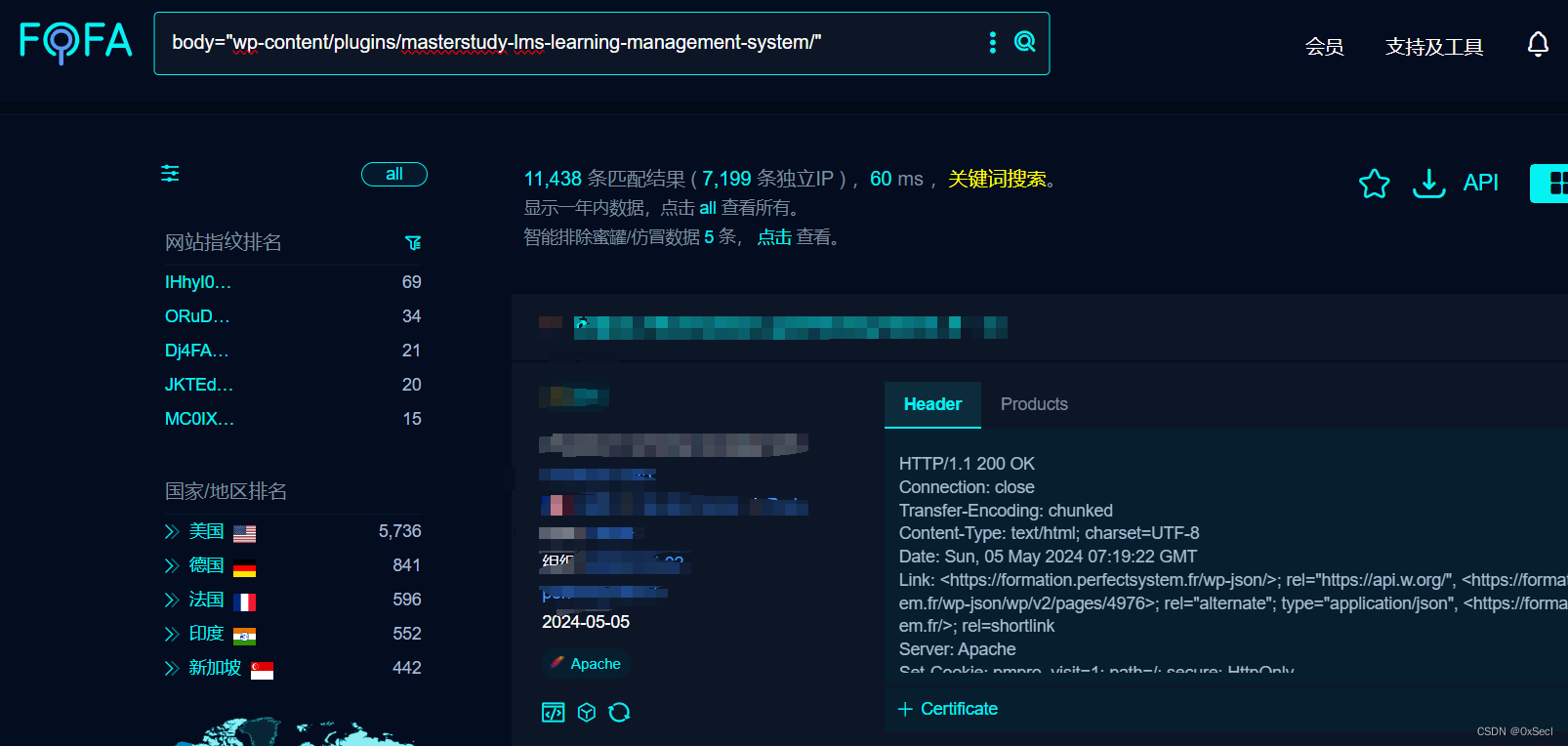
WordPress MasterStudy LMS插件 SQL注入漏洞复现(CVE-2024-1512)
0x01 产品简介 WordPress和WordPress plugin都是WordPress基金会的产品。WordPress是一套使用PHP语言开发的博客平台。该平台支持在PHP和MySQL的服务器上架设个人博客网站。WordPress plugin是一个应用插件。 0x02 漏洞概述 WordPress Plugin MasterStudy LMS 3.2.5 版本及之…...
)
初识Vue-组件通信(详解props和emit)
目录 一、组件通信介绍 1.概念 2.作用 3.特点 4.应用 二、组件通信语法 1.Props 1.1.在子组件中声明 props 1.2.在父组件中传递数据 2.Emit 2.1.在子组件中触发事件 2.2.在父组件中监听事件 三、应用实例 1. 购物车组件 2. 表单数据处理 四、总结 一、组件通信介…...

二叉树的前序、中序、后序遍历的C++实现
二叉树的前序、中序、后序 遍历属于深度优先搜索方式,本文使用递归法实现前序、中序、后序的遍历方法,代码如下: #include <iostream> #include <vector>struct TreeNode{int val;TreeNode* left;TreeNode* right;TreeNode(int …...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
