激励与关怀并行:员工工作动力倍增之道
在现代企业中,员工是推动公司发展的核心力量。如何激发员工的工作动力,使他们在工作中发挥出最大的潜力,一直是企业管理者关注的焦点。实际上,激励与关怀并行的策略,是一种非常有效的提升员工工作动力的方法。
激励是激发员工工作热情的关键。这不仅仅包括物质激励,如提供具有竞争力的薪酬、奖金和福利,更重要的是精神激励。为员工设定明确、可实现的个人和团队目标,让他们感受到自己的工作价值和对公司的贡献。同时,为员工提供学习和发展的机会,帮助他们提升技能和能力,也是激励的重要方面。当员工看到自己的成长和进步,他们会更加投入工作,追求更好的表现。
然而,仅有激励是不够的。在长时间的工作中,员工可能会遇到各种挑战和困难,甚至产生挫败感。这时,管理者的关怀就显得尤为重要。关怀员工,意味着要关注他们的需求和困难,及时给予帮助和支持。当员工感受到来自公司的关怀和支持时,他们会更加感激和忠诚,也会更加努力地工作。
要实现激励与关怀的并行,企业需要建立良好的沟通机制。管理者应该定期与员工进行交流,了解他们的想法和感受,及时发现和解决问题。同时,企业也需要营造积极向上的企业文化,让员工感受到公司的价值观和使命,从而更加投入工作。
另外,激励与关怀并行的策略还需要根据员工的个性和需求进行个性化调整。每个员工都有不同的动机和激励点,管理者需要深入了解员工,为他们量身定制合适的激励和关怀方案。这样,才能最大程度地激发员工的工作动力,实现企业与员工的共同发展。
在实施激励与关怀并行的策略时,企业还需要注意平衡。过度的激励可能会导致员工过分追求个人利益,而忽视团队和公司的整体利益;而过度的关怀则可能让员工产生依赖心理,失去自我成长的动力。因此,管理者需要在激励与关怀之间找到恰当的平衡点,使它们相互促进,共同提升员工的工作动力。
总的来说,激励与关怀并行的策略是提升员工工作动力的有效方法。通过合理的激励和关怀,企业可以激发员工的潜力,提升他们的工作热情和效率,从而推动企业的持续发展。在实施这一策略时,企业需要注意平衡、个性化和沟通等方面的问题,确保激励与关怀能够真正发挥作用,实现企业与员工的共赢。求是达明
相关文章:

激励与关怀并行:员工工作动力倍增之道
在现代企业中,员工是推动公司发展的核心力量。如何激发员工的工作动力,使他们在工作中发挥出最大的潜力,一直是企业管理者关注的焦点。实际上,激励与关怀并行的策略,是一种非常有效的提升员工工作动力的方法。 激励是激…...

软件系统安全设计规范(word原件)
1.1安全建设原则 1.2 安全管理体系 1.3 安全管理规范 1.4 数据安全保障措施 1.4.1 数据库安全保障 1.4.2 操作系统安全保障 1.4.3 病毒防治 1.5安全保障措施 1.5.1实名认证保障 1.5.2 接口安全保障 1.5.3 加密传输保障 1.5.4终端安全保障 软件资料清单列表部分文档…...
做题速度太慢了,面不上
没办法,之前练了一个月的sql。两个月不写,现在差不多忘干净了。工作空窗期,或者休息期不能太久,不然学再多的内容都可能会忘完的。 sql题,腾讯四道sql题,限时45分钟完成。我只做了一道,还没做完…...
Vue 路由
单应用程序 SPA - Single Page Application 所有功能在一个html页面上实现 单页面应用 多用于 系统类网站/内部网站/文档类网站/移动端站点 多页面应用 多用于 公司官网/电商类网站 路由 单页面应用按需更新页面,需要明确访问路径和组件的对应关系 Vue中的路…...

docker-compose-itd和d
docker run -itd和-d的区别 前言: 今天在通过docker-compose启动一基于ubuntu的镜像容器时,发现启动后,容器会一直停止。但是通过docker run -itd是可以正常运行的。基于这个区别,找了一位大神(师傅)问…...
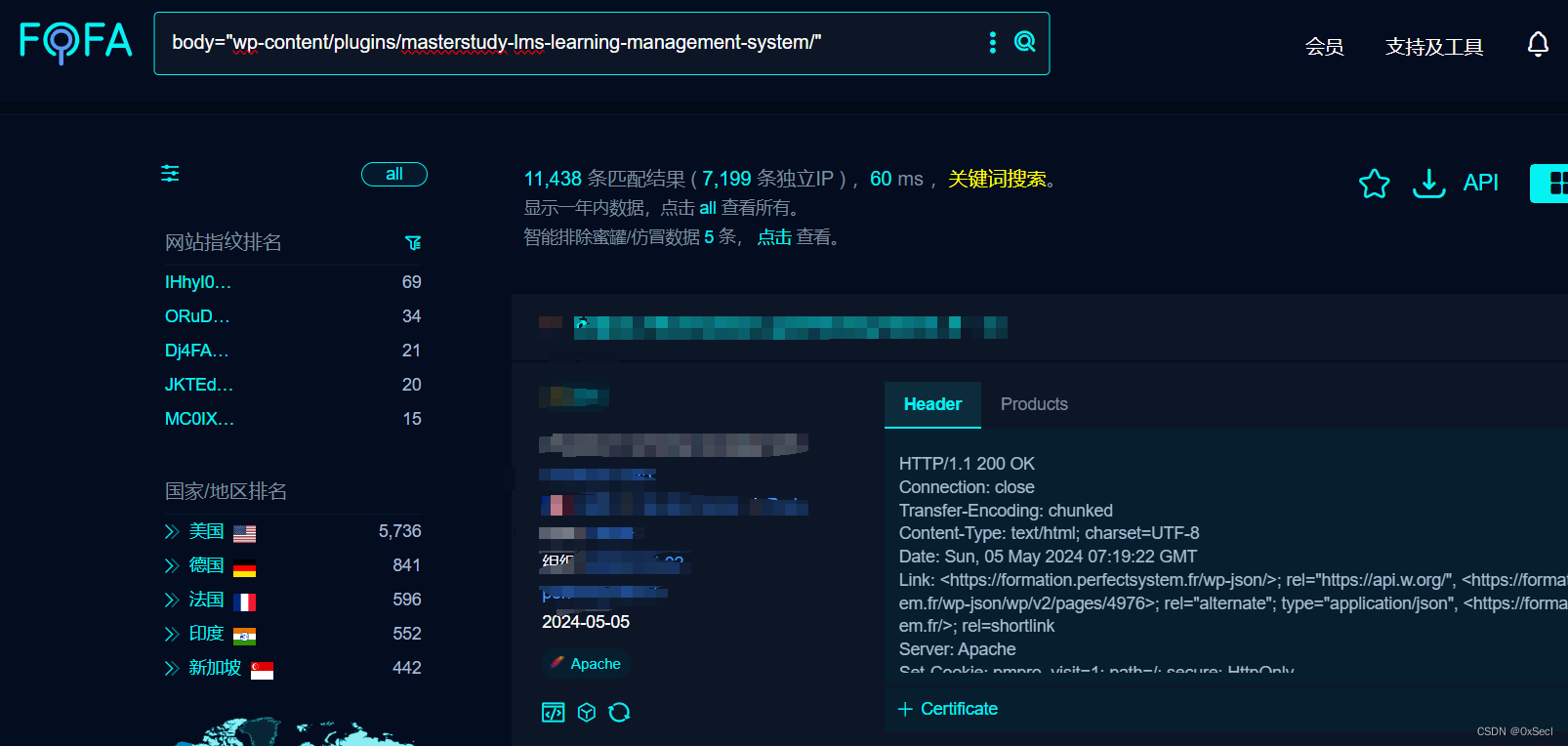
WordPress MasterStudy LMS插件 SQL注入漏洞复现(CVE-2024-1512)
0x01 产品简介 WordPress和WordPress plugin都是WordPress基金会的产品。WordPress是一套使用PHP语言开发的博客平台。该平台支持在PHP和MySQL的服务器上架设个人博客网站。WordPress plugin是一个应用插件。 0x02 漏洞概述 WordPress Plugin MasterStudy LMS 3.2.5 版本及之…...
)
初识Vue-组件通信(详解props和emit)
目录 一、组件通信介绍 1.概念 2.作用 3.特点 4.应用 二、组件通信语法 1.Props 1.1.在子组件中声明 props 1.2.在父组件中传递数据 2.Emit 2.1.在子组件中触发事件 2.2.在父组件中监听事件 三、应用实例 1. 购物车组件 2. 表单数据处理 四、总结 一、组件通信介…...

二叉树的前序、中序、后序遍历的C++实现
二叉树的前序、中序、后序 遍历属于深度优先搜索方式,本文使用递归法实现前序、中序、后序的遍历方法,代码如下: #include <iostream> #include <vector>struct TreeNode{int val;TreeNode* left;TreeNode* right;TreeNode(int …...

golang中数组array和切片slice的区别
go语言中最常用的数据结构 数组array 和 切片 slice的区别对比: 定义和初始化: 数组: [size]类型 切片: []类型 , 数组变量[low:high] var arr1 [3]string{"a", "b", "c"} //…...

LSM-Tree 原理分析
深入浅出分析LSM树(日志结构合并树) - 知乎 写得太好了,留下记录。便于复习。 LSM树详解 - 知乎 多了点点内容,也看看吧。...

【代码随想录37期】Day01 二分查找 + 移除元素
二分查找 力扣704 贴一下之前的笔记: 没想到一下子写不出来,忘记什么是二分法了,这里回顾一下: 「二分查找 binary search」是一种基于分治策略的高效搜索算法。 它利用数据的有序性,每轮减少一半搜索范围ÿ…...

GitPython 使用教程
GitPython 使用教程 GitPython 是一个用于与 Git 版本控制系统进行交互的 Python 库。它提供了简单的接口,让你可以通过 Python 代码执行 Git 命令和操作 Git 仓库。 1. 安装 GitPython 你可以使用 pip 在命令行中安装 GitPython: pip install gitpy…...

MATLAB 基于规则格网的点云抽稀方法(自定义实现)(65)
MATLAB 基于规则格网的点云抽稀方法(自定义实现)(65) 一、算法介绍二、算法实现1.代码2.结果一、算法介绍 海量点云的处理,需要提前进行抽稀预处理,相比MATLAB预先给出的抽稀方法,这里提供一种基于规则格网的自定义抽稀方法,步骤清晰,便于理解抽稀内涵, 主要涉及到使…...
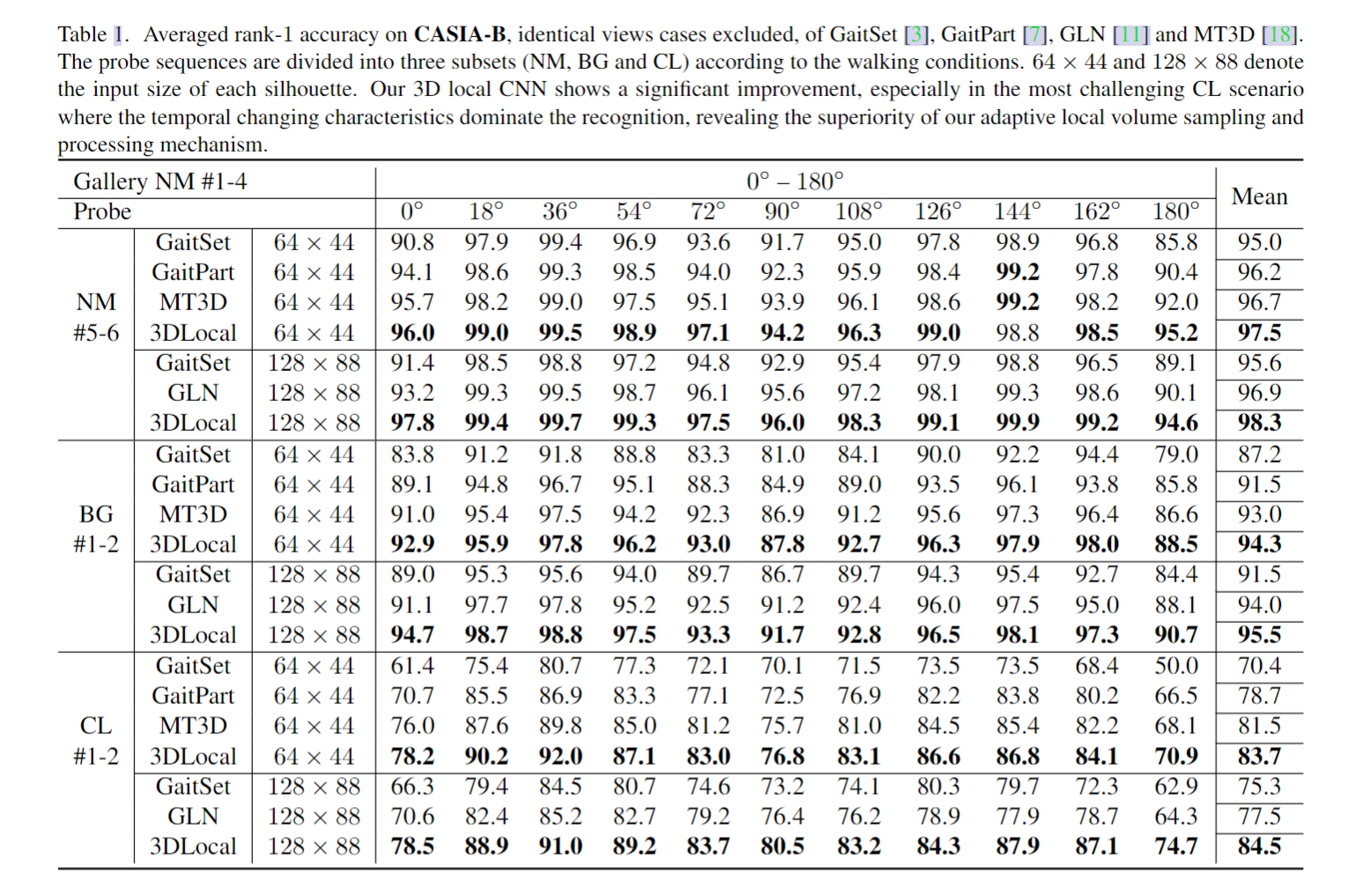
论文阅读】 ICCV-2021-3D Local Convolutional Neural Networks for Gait Recognition
motivation :现有方法方法无法准确定位身体部位,不同的身体部位可以出现在同一个条纹(如手臂和躯干),一个部分可以出现在不同帧(如手)的不同条纹上。其次,不同的身体部位具有不同的尺度,即使是不同帧中的同一部分也可以出现在不同…...
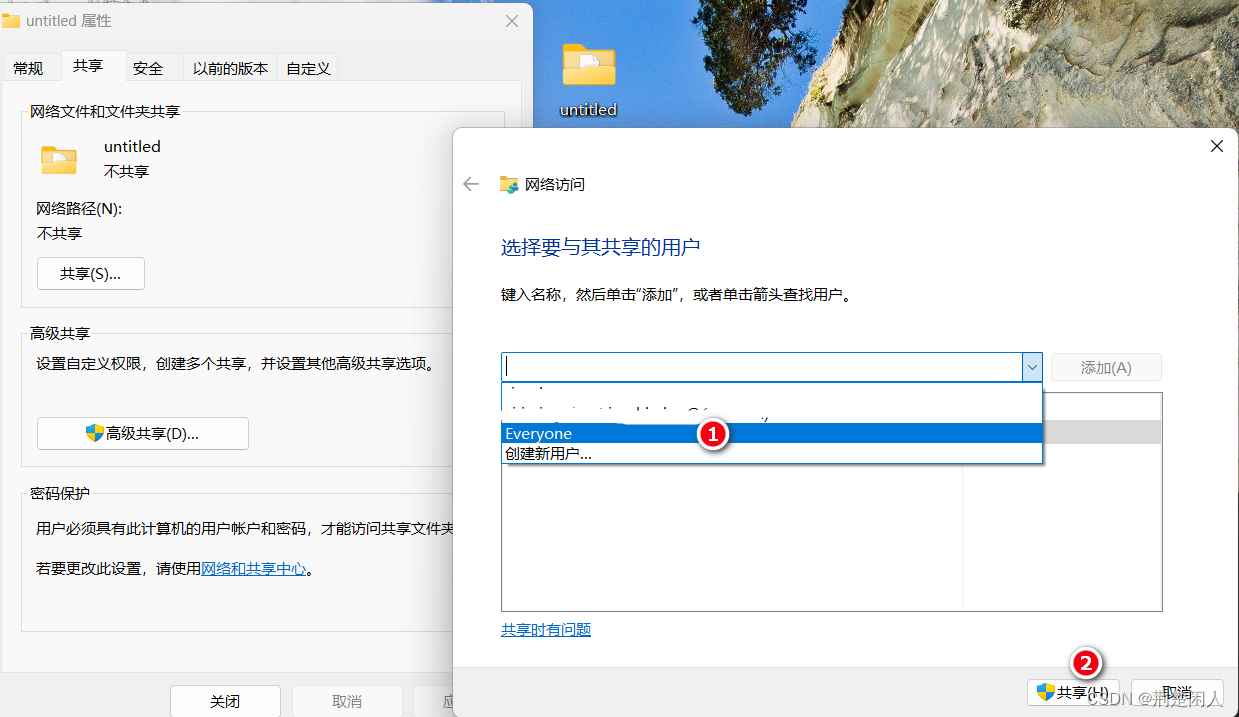
同一局域网如何从Windows系统拷贝文件到银河麒麟系统
1. 先将Windows下的、被拷贝文件所在文件夹设置为共享目录:在文件夹上单击右键选择“属性”菜单,弹出如下对话框: 按数字顺序单击鼠标左键,弹出如下对话框: 并将权限开放为Everyone,单击“共享”按钮。 在…...
-OD统一考试(C卷D卷))
2024年华为OD机试真题-数的分解-(C++)-OD统一考试(C卷D卷)
题目描述: 给定一个正整数n,如果能够分解为m(m > 1)个连续正整数之和,请输出所有分解中,m最小的分解。 如果给定整数无法分解为连续正整数,则输出字符串"N"。 输入描述: 输入数据为一整数,范围为(1, 2^30] 输出描述: 比如输入为: 21 输出: 21=10+11 补…...
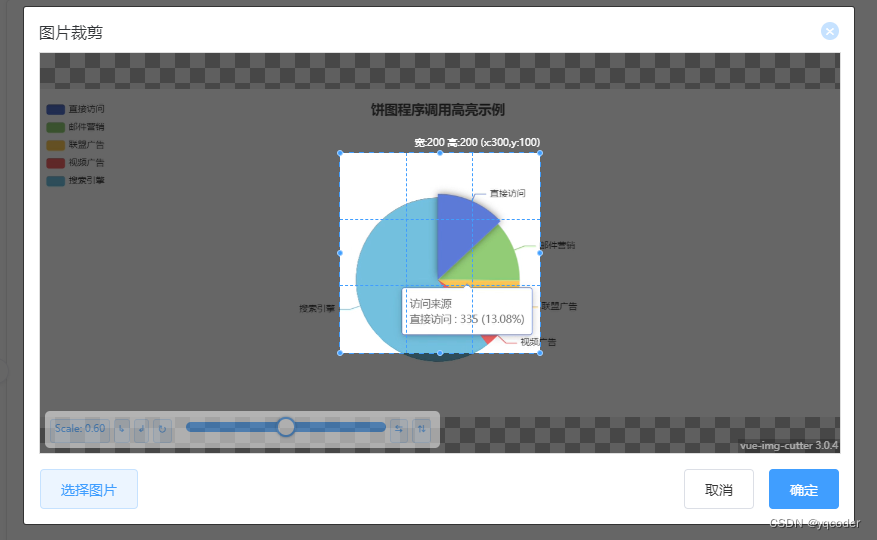
vue-img-cutter 图片裁剪详解
前言:vue-img-cutter 文档,本文档主要讲解插件在 vue3 中使用。 一:安装依赖 npm install vue-img-cutter # or yarn add vue-img-cutter # or pnpm add vue-img-cutter 二:构建 components/ImgCutter.vue 组件 <script se…...

PCL 点云中的平面点云提取
平面点云提取 一. 索引提取1.1 算法概念1.2 算法流程1.3 主要函数二.代码示例三.结果示例一. 索引提取 1.1 算法概念 平面点云提取:是指从点云数据中提取出属于平面的点的过程。 1.2 算法流程 使用pcl::SACSegmentation类进行点云分割的基本步骤如下: 创建一个pcl::SACSegm…...
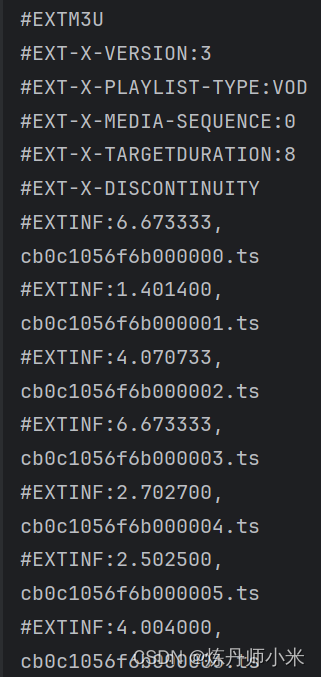
4.用python爬取保存在text中的格式为m3u8的视频
文章目录 一、爬取过程详解1.寻找视频的m3u8链接2.从网页源码中寻找视频的m3u8链接的第二部分内容3.从视频的m3u8链接获取视频 二、完整的代码 一、爬取过程详解 1.寻找视频的m3u8链接 这个文档承接了爬虫专栏的 第一节.python爬虫爬取视频网站的视频可下载的源url࿰…...
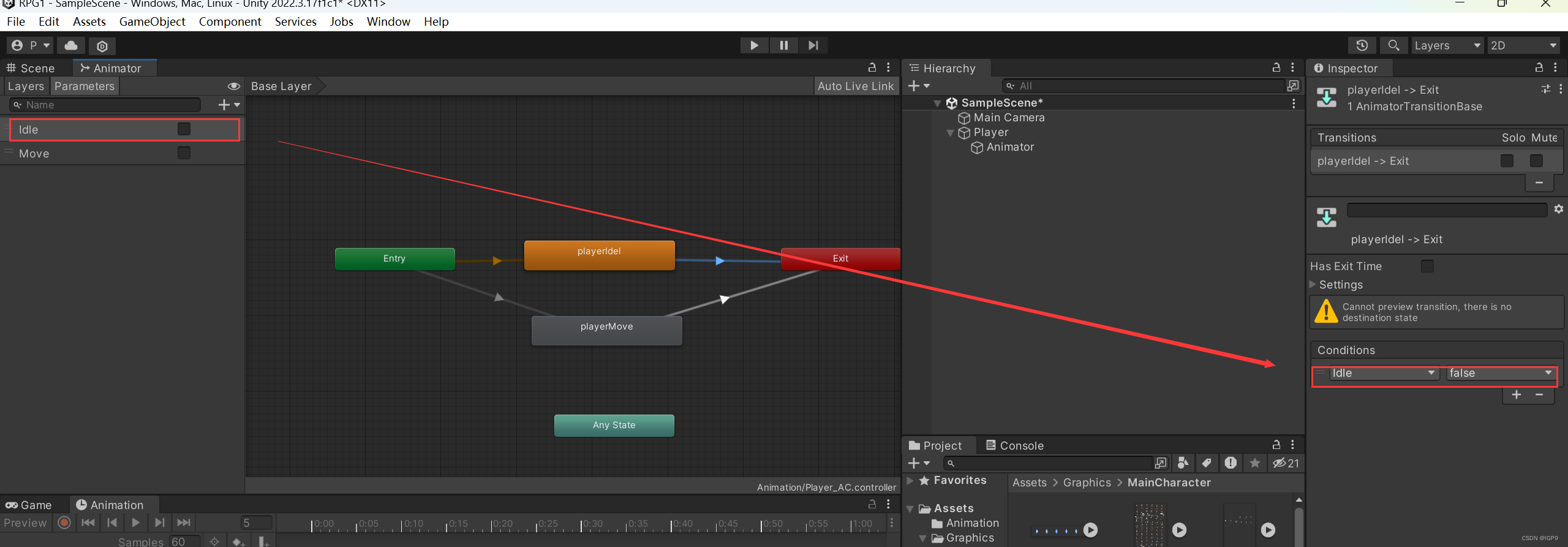
240503-关于Unity的二三事
240503-关于Unity的二三事 1 常用快捷键 快捷键描述CtrlP播放/停止Ctrl1打开Scene窗口Ctrl2打开Game窗口Ctrl3打开Inspect窗口Ctrl4打开Hierarchy窗口Ctrl5打开Project窗口Ctrl6打开Animation窗口 2 关联VisualStudio2022 3 节约时间:将最新声明的参数移动到最上…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
