codeforce#938 (div3) 题解
C. Inhabitant of the Deep Sea
数组第一个元素减一下,最后一个元素减一下,一共能减k次,问有多少元素能减到0.细节模拟我是傻逼,有问题建议直接看tc面像tc编程
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;int n;
ll k;
ll store[maxn];
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>k;rep(i,0,n) cin>>store[i];ll m_right = k/2LL;ll m_left = m_right + k % 2LL;int ans = 0;int inf = 0, sup = n-1;while((m_right>0 || m_left>0) && inf<=sup) {if (inf == sup) {if (m_right + m_left >= store[inf]) {ans ++;}break;}if (m_left >= store[inf]) {ans ++;m_left -= store[inf];inf ++;} else {store[inf] -= m_left;m_left = 0;}if (m_right >= store[sup]) {ans ++;m_right -= store[sup];sup --;} else {store[sup] -= m_right;m_right = 0;}}cout<<ans<<endl;}return 0;
}
D. Inaccurate Subsequence Search
给数组a和数组b,问a中有多少子数组在重排后有至少k个元素相同。
滑动窗口。首先遍历b得出有多少种字母以及每个字母有多少。然后滑动窗口维护窗口内字母的个数,窗口前进时pop首位push末尾,update维护信息,然后每次窗口移动进行对比是否符合条件
finish
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;const int sub_maxn = 1e6+5;int n,k,m;
int store[maxn], partten[maxn];
map<int,bool> matches;
map<int, int> used, have;
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>m>>k;rep(i,0,n) cin>>store[i];rep(i,0,m) cin>>partten[i];matches.clear();used.clear();rep(i,0,m)if (matches[partten[i]]) {have[partten[i]] ++;} else {matches[partten[i]] = true;have[partten[i]] = 1;}int pos = 0,match_num = 0;int ans = 0;while(pos<n) {int num = store[pos];if (pos < m) {if (matches[num]) {if(used[num] < have[num]) match_num ++;used[num] ++;}} else {
// cout<<"pos:"<<pos<<" match:"<<match_num<<endl;if (match_num >= k) {ans ++;}// popint pop_pos = pos - m;int pop_num = store[pop_pos];if (matches[pop_num]){used[pop_num] --;if (used[pop_num] < have[pop_num]) match_num --;}// pushif (matches[num]) {if(used[num] < have[num]) match_num ++;used[num] ++;}}pos ++;}if (match_num >= k) ans ++;cout<<ans<<endl;}return 0;
}
E. Long Inversions
给出一个二进制序列s,每次可以选择长度为k的连续子列取反,问能让s的每一位都变成1的最大k是多少
枚举暴力k值,倒序遍历n,发现可以直接输出。毕竟 n 2 n^2 n2也不大。
然后再说下怎么验证可以让s全变1.当我们在s中发现一个0,那么肯定是要反转一次的,然后继续下一位,这样全部遍历一遍看还有没有0,没有就是可以
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 5e3+5;string store;
bool check(int);
int main() {IOSint t;cin>>t;while(t--) {int n;cin>>n;cin>>store;int inf = n;drep(inf,n,0) {if(check(inf)) {cout<<inf<<endl;break;}}}return 0;
}
bool check(int k) {int pos = 0;int len = store.length();vector<int> cnt(len+1,0);int inv_cnt = 0;bool res = true;while(pos<len) {inv_cnt += cnt[pos];int num = store[pos] - '0';if (inv_cnt%2)num = num ^ 1;if (!num) {if (pos+k<=len) {inv_cnt ++;cnt[pos+k] = -1;} else {res = false;break;}}pos ++;}return res;
F. Unfair Game
给一堆1234,如果这些数XOR结果是0会赢,现在每次拿走一个,问最多能赢几次。
显然4和123不属于一类,单纯考虑4,那么就赢4的个数/2次。然后我们来看123.
记dp[i][j][k]为1个数为i个,2个数为j,3个数为k时赢的次数。初始dp[0][0][0]为0。当且仅当i个1,j个2,k个3XOR时dp[i][j][k] + 1(由于XOR性质,这里只需要判断奇偶再运算就可以),转移方程
d p [ i ] [ j ] [ k ] = m a x ( d p [ i − 1 ] [ j ] [ k ] , d p [ i ] [ j − 1 ] [ k ] , d p [ i ] [ j ] [ k − 1 ] dp[i][j][k] = max(dp[i-1][j][k], dp[i][j-1][k], dp[i][j][k-1] dp[i][j][k]=max(dp[i−1][j][k],dp[i][j−1][k],dp[i][j][k−1]
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;int p[5];
int dp[205][205][205];
void pre();
int main() {IOSpre();int t;cin>>t;while(t--) {rep(i,0,4) cin>>p[i];int ans = p[3] / 2 + dp[p[0]][p[1]][p[2]];cout<<ans<<endl;}return 0;
}
void pre() {int lim = 201;dp[0][0][0] = -1;rep(i,0,lim) {rep(j,0,lim) {rep(k,0,lim) {if (i) dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][k]);if (j) dp[i][j][k] = max(dp[i][j][k], dp[i][j-1][k]);if (k) dp[i][j][k] = max(dp[i][j][k], dp[i][j][k-1]);int ans = ((i&1) * 1 ) ^ ((j&1) * 2) ^ ((k&1) * 3);if (!ans)dp[i][j][k] ++;}}}
}
G. GCD on a grid
求从(1,1)到(n,m)的最大公约数。
这个题其实也是枚举,但是根据题意,答案一定是(1,1)和(n,m)公约数的因数。
然后我们拿着因数num对整个矩阵求余,看有没有一条路径从(1,1)到(n,m)上所有的元素都是num的倍数,如果有,那么就是候选答案,遍历所有因数后从候选答案选最大。
至于路径的查询用的dp。记dp[i][j]为(i,j)是否是因数num的倍数。当且仅当 s t o r e [ i ] [ j ] m o d n u m store[i][j] \mod num store[i][j]modnum为true,转移方程
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] ∥ d p [ i ] [ j − 1 ] dp[i][j] = dp[i-1][j] \parallel dp[i][j-1] dp[i][j]=dp[i−1][j]∥dp[i][j−1]
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 128;ll gcd(ll,ll);int n,m;
int store[maxn][maxn];
bool dp[maxn][maxn];
void init();
void show();
bool check(int);
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>m;rep(i,0,n) rep(j,0,m)cin>>store[i][j];int ans = 1;int num = gcd(store[0][0], store[n-1][m-1]);int lim = sqrt(num);for(int i=1;i*i<=num;i++) {if (num % i) continue;if (check(i)) {ans = max(ans, i);}if (check(num/i))ans = max(ans, num/i);}cout<<ans<<endl;}return 0;
}
ll gcd(ll a, ll b){ll t;while(b){t = b;b = a % b;a = t;}return a;
}
void init() {rep(i,0,n) rep(j,0,m) dp[i][j] = false;
}
void show() {rep(i,0,n) {rep(j,0,m) cout<<dp[i][j]<<' ';cout<<endl;}
}
bool check(int num) {if (num == 1) return true;rep(i,0,n) {rep(j,0,m) {dp[i][j] = (store[i][j] % num) == 0;bool tmp = false;if (i && dp[i-1][j]) tmp = tmp || dp[i-1][j];if (j && dp[i][j-1]) tmp = tmp || dp[i][j-1];if (i || j) dp[i][j] = dp[i][j] && tmp;}}return dp[n-1][m-1];
}
相关文章:
 题解)
codeforce#938 (div3) 题解
C. Inhabitant of the Deep Sea 数组第一个元素减一下,最后一个元素减一下,一共能减k次,问有多少元素能减到0.细节模拟我是傻逼,有问题建议直接看tc面像tc编程 #include <iostream> #include <string.h> #include &…...
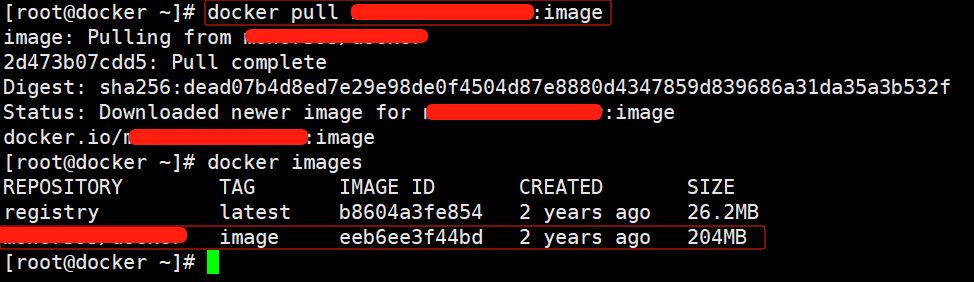
【Docker】如何注册Hub账号并上传镜像到Hub仓库
一、创建Hub账户 浏览器访问:hub.docker.com 点击【Sign up】注册账号 输入【邮箱】【用户名】【密码】 ps:用户名要有字母数字;订阅不用勾选 点击【Sign up】注册即可 点击【Sign in】登录账号 输入【邮箱】【密码】 点击【Continue】登录 二…...
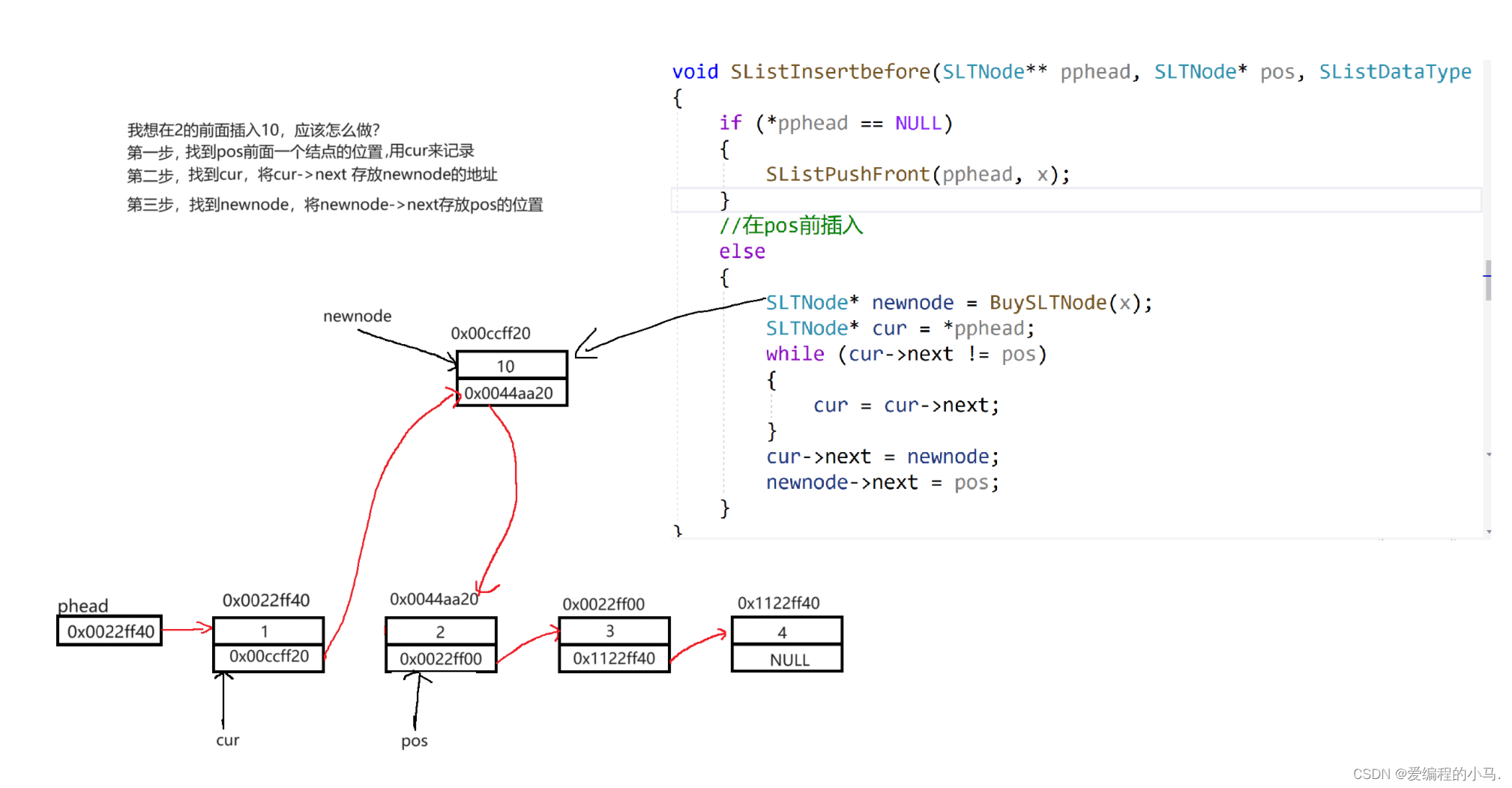
[初阶数据结构】单链表
前言 📚作者简介:爱编程的小马,正在学习C/C,Linux及MySQL。 📚本文收录于初阶数据结构系列,本专栏主要是针对时间、空间复杂度,顺序表和链表、栈和队列、二叉树以及各类排序算法,持…...

项目使用git开发流程
第一步 项目初期:领导负责的工作 01 创建仓库:在码云上面创建仓库地址,创建完成后点击初始化README:郝陶涛/vue-tea 02 领导在桌面上将代码克隆下来:将代码克隆下来之后,切换到代码内部,使用g…...

Day 28 MySQL的数据备份与恢复
数据备份及恢复 1.概述 所有备份数据都应放在非数据库本地,而且建议有多份副本 备份: 能够防止由于机械故障以及人为误操作带来的数据丢失,例如将数据库文件保存在了其它地方 冗余: 数据有多份冗余,但不等备份&…...
疑问篇)
PackageKit的使用(三)疑问篇
本篇主要是一些疑问归纳,不做具体的函数分析,但是会给出关键点,查看源码就会很清楚了 apt source PackageKit 1. org.freedesktop.PackageKit D-Bus 接口介绍 D-Bus API Reference: PackageKit Reference Manual c库的接口可以看源码。 2.…...

【Linux】17. 进程间通信 --- 管道
1. 什么是进程间通信(进程间通信的目的) 数据传输:一个进程需要将它的数据发送给另一个进程 资源共享:多个进程之间共享同样的资源。 通知事件:一个进程需要向另一个或一组进程发送消息,通知它(它们)发生了…...
有哪些有效的复习方法可以帮助备考软考?
软考目前仍然是一个以记忆为主、理解为辅的考试。学过软考的朋友可能会感到困惑,因为软考的知识在日常工作中有许多应用场景,需要理解的地方也很多。但为什么我说它是理解为辅呢?因为这些知识点只要记住了,都不难理解,…...

【MySQL | 第九篇】重新认识MySQL锁
文章目录 9.重新认识MySQL锁9.1MySQL锁概述9.2锁分类9.2.1锁的粒度9.2.2锁的区间9.2.3锁的性能9.2.4锁的级别 9.3拓展:意向锁9.3.1意向锁概述9.3.2意向锁分类9.3.3意向锁作用(1)意向锁的兼容互斥性(2)例子1(…...

含义:理财风险等级R1、R2、R3、R4、R5
理财风险等级R1、R2、R3代表什么,为什么R1不保本,R2可能亏损 不尔聊投资https://author.baidu.com/home?frombjh_article&app_id1704141696580953 我们购买理财产品的时候,首先都会看到相关产品的风险等级。风险等级约定俗成有5级&…...

ICode国际青少年编程竞赛- Python-2级训练场-列表入门
ICode国际青少年编程竞赛- Python-2级训练场-列表入门 1、 Dev.step(3)2、 Flyer.step(1) Dev.step(-2)3、 Flyer.step(1) Spaceship.step(7)4、 Flyer.step(5) Dev.turnRight() Dev.step(5) Dev.turnLeft() Dev.step(3) Dev.turnLeft() Dev.step(7) Dev.turnLeft() Dev.…...
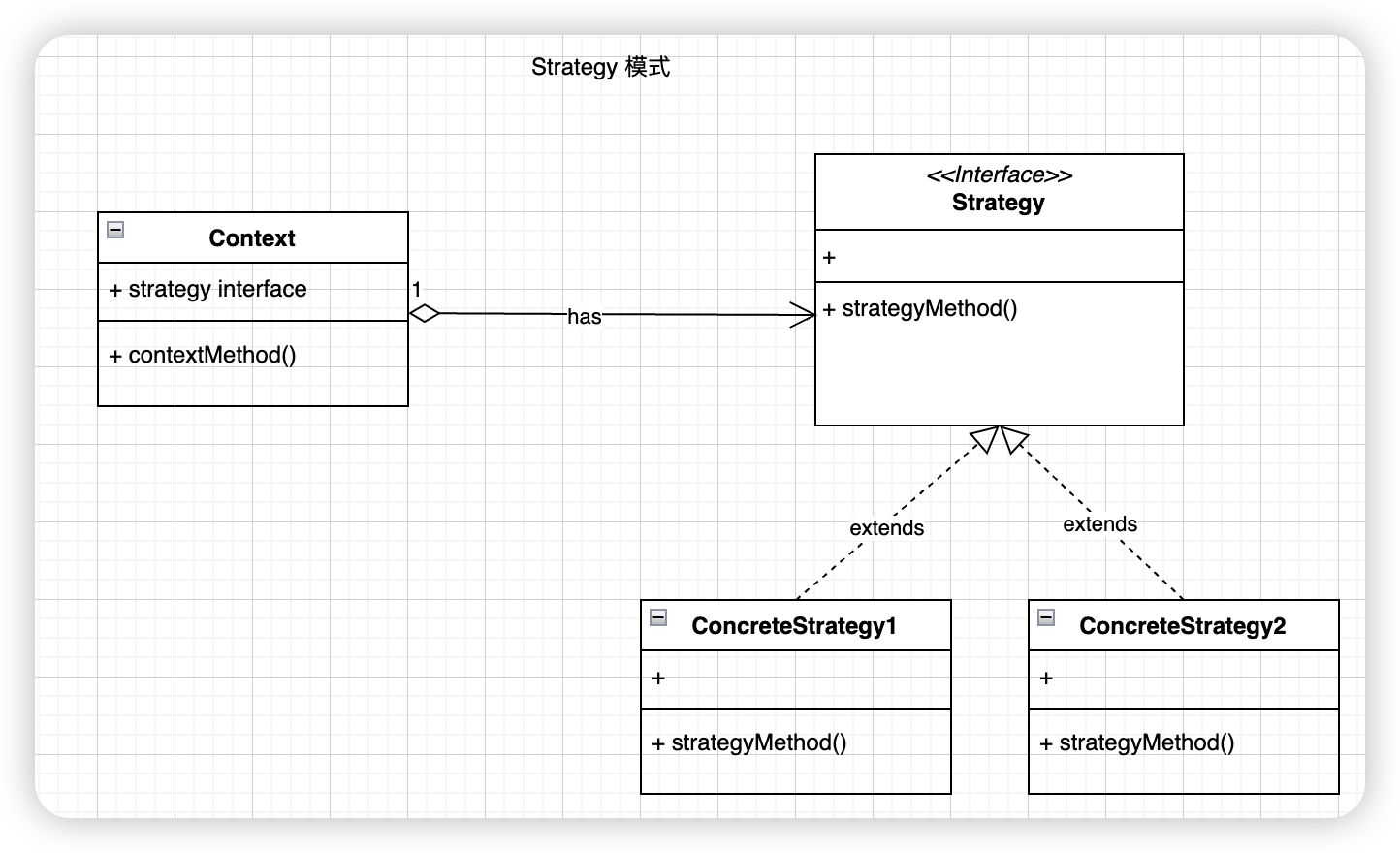
【设计模式】14、strategy 策略模式
文章目录 十四、strategy 策略模式14.1 map_app14.1.1 map_app_test.go14.1.2 map_app.go14.1.3 navigate_strategy.go 十四、strategy 策略模式 https://refactoringguru.cn/design-patterns/strategy 需求: client 知道很多不同的策略, 希望在运行时切换. 场景示例: 就像高…...
C++类和对象(基础篇)
前言: 其实任何东西,只要你想学,没人能挡得住你,而且其实学的也很快。那么本篇开始学习类和对象(C的,由于作者有Java基础,可能有些东西过得很快)。 struct在C中的含义: …...

Oracle导入数据中文乱码问题处理,修改客户端字符编码跟数据库的一致
前提:SQL文件打开其中中文字符是正常显示,保证导出文件中文字符正常。通过sqlplus命令导入SQL文件出现乱码,这是因为客户端跟数据库的字符集不一致导致出现乱码问题。 要SQL导入的中文正常,要确保执行导入命令的客户端字符编码跟…...
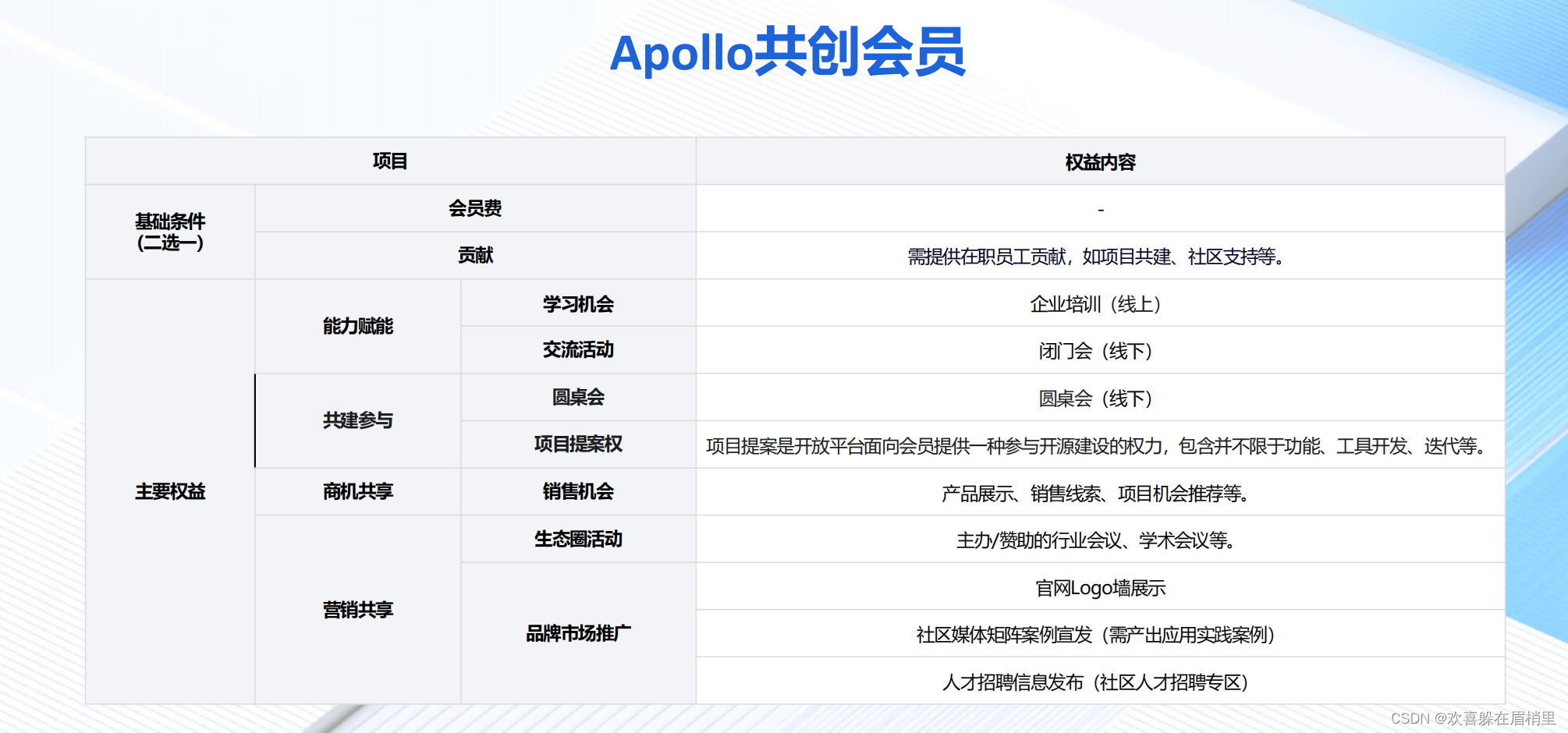
【与 Apollo 共创生态:展望自动驾驶全新未来】
1、引言 历经七年的不懈追求与创新,Apollo开放平台已陆续推出了13个版本,汇聚了来自全球170多个国家与地区的16万名开发者及220多家合作伙伴。随着Apollo开放平台的不断创新与发展,Apollo在2024年4月19日迎来了Apollo开放平台的七周年大会&a…...
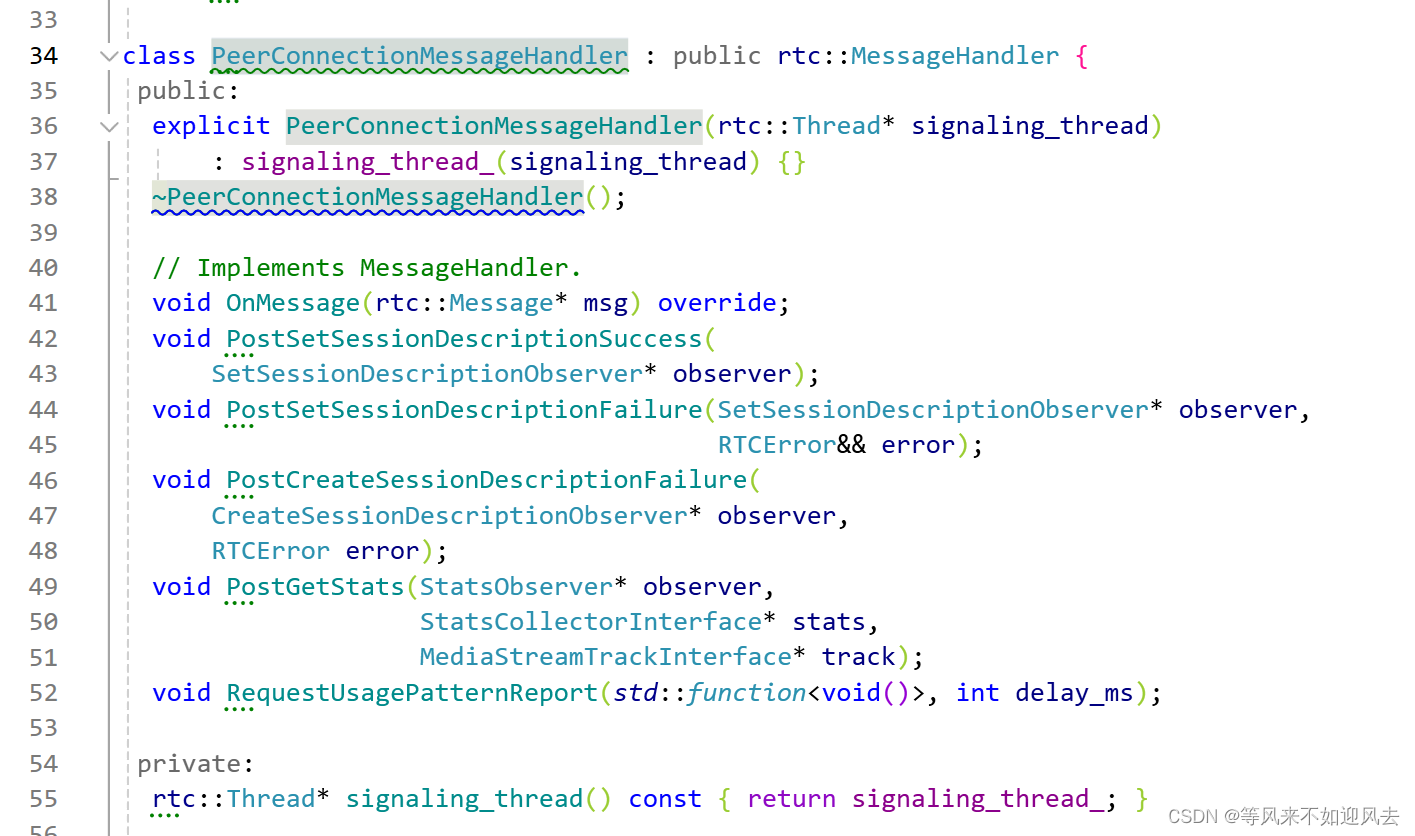
【webrtc】MessageHandler 5: 基于线程的消息处理:以PeerConnection信令线程为例
peerconn的信令是通过post 消息到自己的信令线程消息来处理的PeerConnectionMessageHandler 是具体的处理器G:\CDN\rtcCli\m98\src\pc\peer_connection_message_handler.hMachinery for handling messages posted to oneself PeerConnectionMessageHandler 明确服务于 signalin…...

计算机网络 3.2网络体系结构
第二节 网络体系结构 一、网络协议 1.定义: ①通信双方共同遵守的规则。 ②为网络数据交换制定的规则、约定与标准。 ③网络实体之间通信时有关信息传输顺序、信息格式、信息内容的约定或规则。 2.协议三要素: 语法:确定协议元素的格式…...
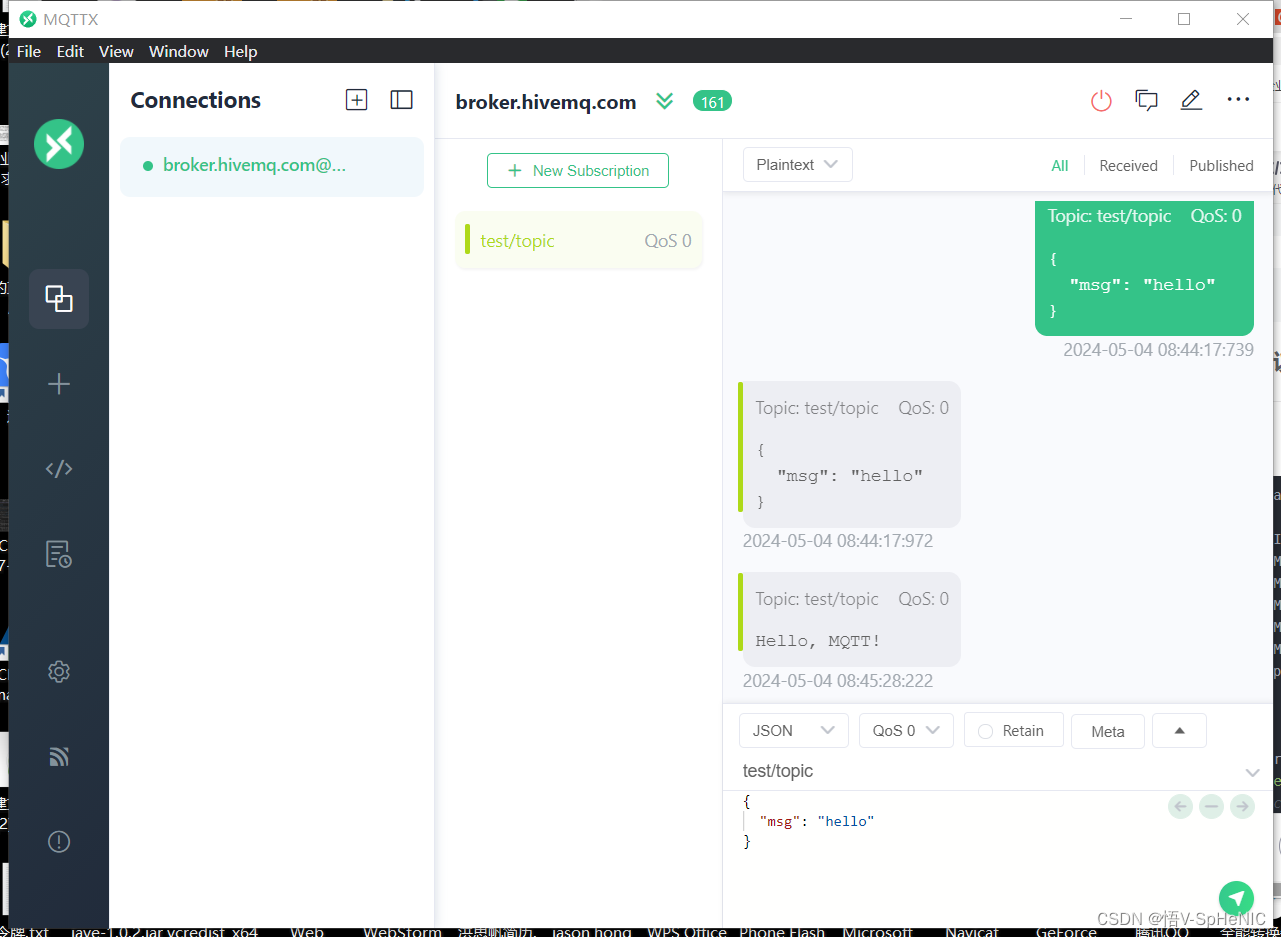
连接HiveMQ代理器实现MQTT协议传输
先下载MQTTX: MQTTX: Your All-in-one MQTT Client Toolbox 使用线上免费的MQTTX BROKER:The Free Global Public MQTT Broker | Try Now | EMQ 打开MQTTX,创建连接,点击NEW SUBSCRIPTION,创建一个主题,这里使用test/topic,在下面Json中填写…...
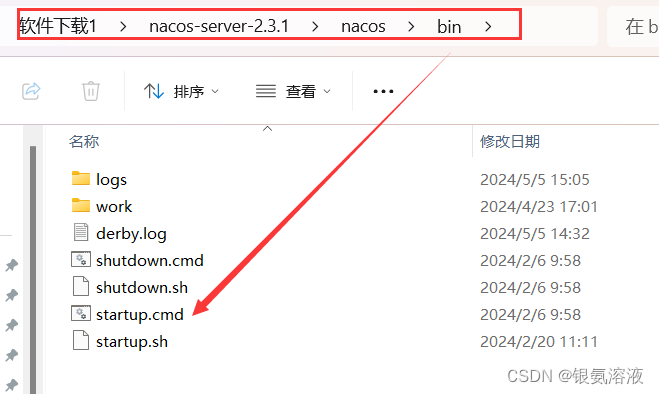
springcloud报错:Failed to start bean‘webServerStartStop‘
如果你正在使用nacos进行服务注册,然后报一下错误: 那就说明的nacos没有打开,所以找到你的下载nacos的文件夹 好了,错误完美解决~...

el-checkbox 无法动态设置勾选状态
问题 cheked 值动态变化,但是勾选状态无法动态改变 解决 v-model 与:checked 同时使用 <el-checkbox class"add-shop-check" v-model"renderData[0].isCheck" :checked"renderData[0].isCheck" change"checked > selec…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...

AGV|无人叉车工业语音播报器|预警提示器LBE-LEX系列性能与接线说明
LBE-LEX系列AGV|无人叉车工业语音播报器|预警提示器,涵盖LBE-LEI-M-00、LBE-LESM-00、LBE-LES-M-01、LBE-LEC-M-00、LBE-KEI-M-00、LBE-KES-M-00、LBE-KES-M-01、LBE-KEC-M-00等型号,适用于各种需要语音提示的场景,主要有AGV、AMR机器人、无人…...
