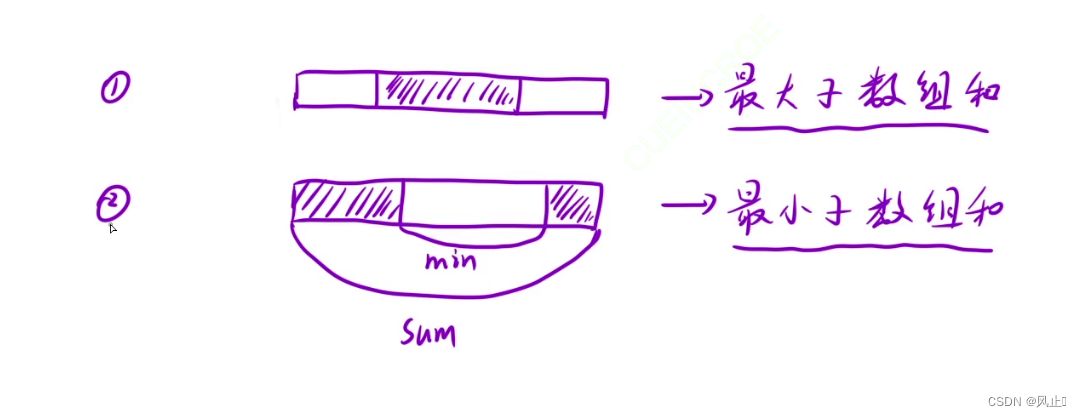
对于子数组问题的动态规划
前言
先讲讲我对于这个问题的理解吧
当谈到解决子数组问题时,动态规划(DP)是一个强大的工具,它在处理各种算法挑战时发挥着重要作用。动态规划是一种思想,它通过将问题分解成更小的子问题并以一种递归的方式解决它们,然后利用这些解决方案来构建原始问题的解。在动态规划中,我们经常会遇到两种状态:一种是单独成一段,另一种是以 i 结尾的子数组。
通过枚举和动态规划,我们可以有效地解决子数组问题。枚举法需要考虑所有可能的子数组组合,然后比较它们以找到最优解。这种方法通常需要较多的时间和空间,因为它需要枚举所有可能性。而动态规划则更加智能化,它通过保存历史记录来避免不必要的重复计算。这样,下次遍历时,我们可以利用之前的计算结果,从而大大提高了效率。
动态规划的一个常见技巧是前缀和,它可以帮助我们快速求出数组中任意子数组的和。前缀和的核心思想是将原始数组中每个位置的值累加起来,形成一个新的数组,然后利用这个新数组来快速计算子数组的和。这种方法在处理求子数组和的问题时非常实用,因为它将复杂度降低到了单一状态的动态规划。
另外,预处理也是动态规划中常用的技巧之一。通过将经常使用的数据存储起来,我们可以在需要时快速获取,从而减少计算时间。预处理的思想是在问题出现之前就对数据进行处理,以便在需要时能够迅速获取所需的信息。
综上所述,动态规划是一种强大的解决子数组问题的方法,通过合理利用枚举、动态规划、前缀和和预处理等技巧,我们可以高效地解决各种复杂的算法挑战,为问题提供简单明了的解决方案。
这是我记得笔记

我准备了五道例题都是这些解决方案
1.求最大子数组的和
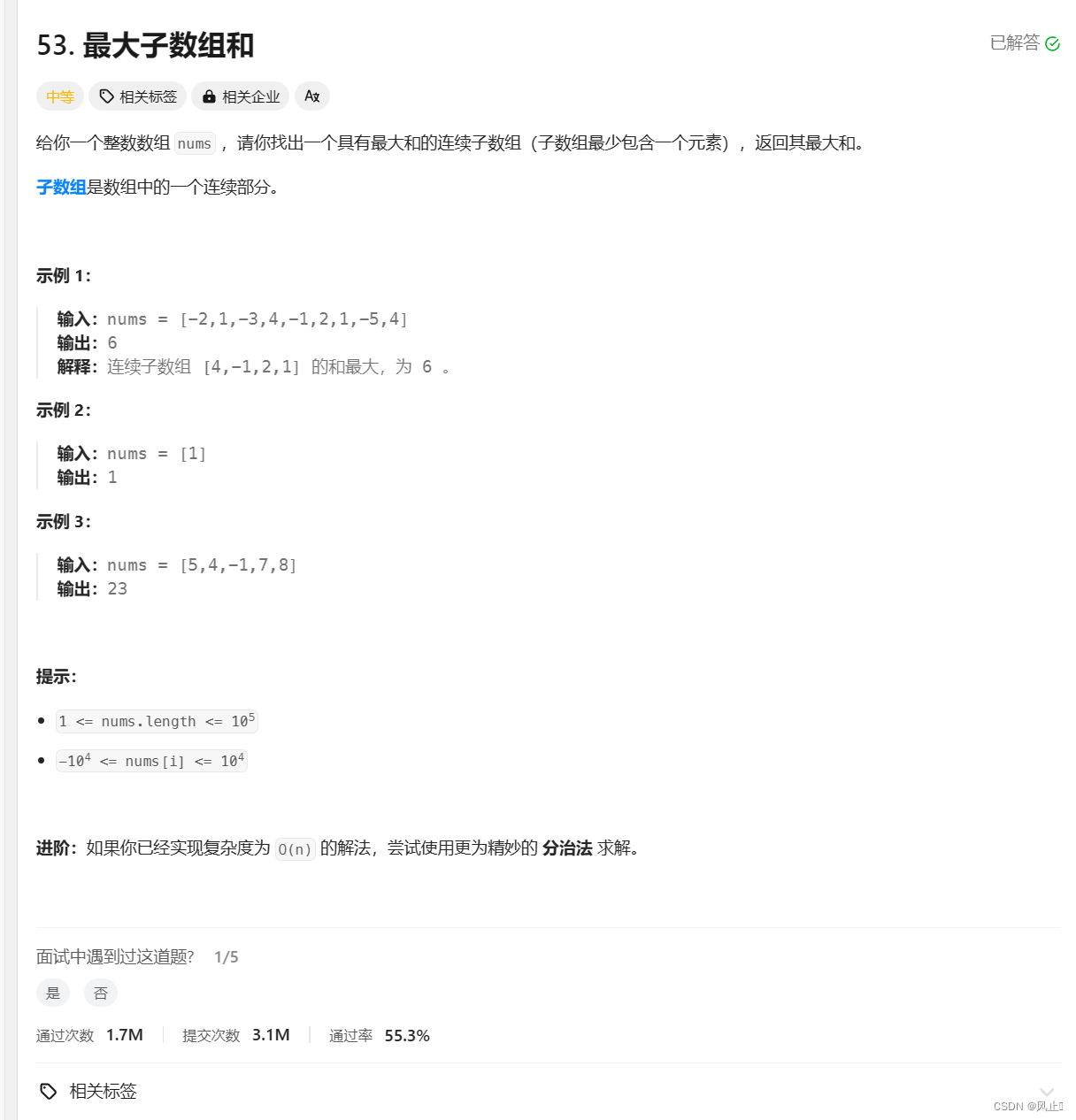
. - 力扣(LeetCode)
思路分析:这一题主要是使用动态规划,也可以使用前缀和,动态规划也是求子数组的普遍思路,有两种状态,1自己组成子数组 和 前面的组成子数组,所以状态转移方程也就是Max(nums[i],dp[i - 1] + nums[i])
代码实现
public int maxSubArray(int[] nums) {int n = nums.length;int[] dp = new int[n + 1];//以i位置为结尾的最大子数组和 (多状态 前面i - 1的子数组要 和 不要)// 初始化 (因为存在负数)dp[0] = -0x3f3f3f3f;//前面子数组都是以i - 1位置为结尾 或者 i位置自己构成一个数组for (int i = 1; i <= nums.length; i++) {dp[i] = Math.max(nums[i - 1], dp[i - 1] + nums[i - 1]);}int max = -0x3f3f3f3f;for (int i = 0; i < dp.length; i++) {max = Math.max(dp[i], max);}return max;}2.求最大环形子数组

. - 力扣(LeetCode)
思路分析:
中间的是连续的所以求内部最小子数组和就好了, 或者中间成最大子数组和 //f[]表示以i位置为结尾的所有子数组中的最大值 //g[]表示以i位置为结尾的所有子数组中的最小值 //g[]就是为了处理边界。他通过计算中间部分的最小值来结算环的最大值
public int maxSubarraySumCircular(int[] nums) {int sum = 0;//用来处理最小值int n = nums.length;//1.状态表示int[] f = new int[n + 1],g = new int[n + 1];//2.状态转移方程 自己组成子数组 和 自己加上以 i-1位置结尾 的最大子数组//3.初始化 = 0 即可for (int i = 1; i <= n; i++) {f[i] = Math.max(f[i - 1] + nums[i - 1], nums[i - 1]);g[i] = Math.min(g[i - 1] + nums[i - 1], nums[i - 1]);sum += nums[i - 1];}int maxF = -0x3f3f3f3f;//统计结果int minG = 0x3f3f3f3f;//统计结果//可以和上面统一合并,一个循环就够了for (int i = 1; i <= n; i++) {maxF = Math.max(maxF,f[i]);minG = Math.min(minG,g[i]);}//为了防止全是负数返回0,所以sum - minG要和0做判断//因为 -8 - (-8) = 0;全是负数sum = -8 minG = -8 所以要返回maxFreturn Math.max(maxF,sum - minG == 0 ? maxF : sum - minG);}3.和为k的子数组个数
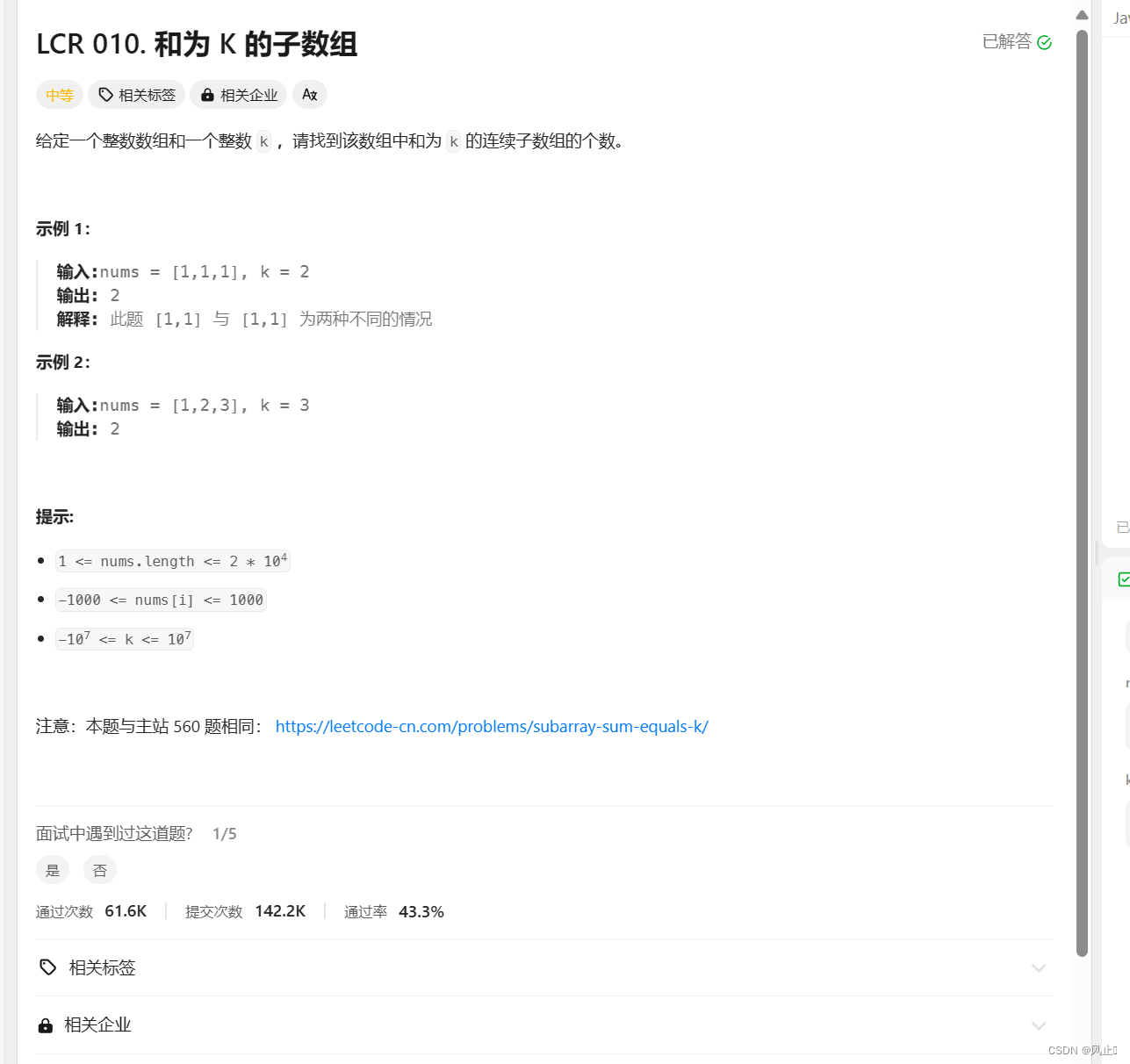
. - 力扣(LeetCode)
思路分析:
//解法 动态规划 + hash表 k == pre[i](i位置的前缀和) - pre[j - 1] //此时 [j,i]的子数组为k
public int subarraySum(int[] nums, int k) {int count = 0;//统计出现了多少次int n = nums.length;HashMap < Integer, Integer > hash = new HashMap<>();//当词典使用,存储所有前缀和hash.put(0,1);//记录0出现了1次,防止前缀和单独构成答案//1.状态表示 以i位置为结尾的区间和int[] pre = new int[n + 1];//2.状态转移方程 pre[i] = pre[i - 1] + nums[i]//3.初始化 防止j - 1 越界 pre[0] = 0for (int i = 1; i <= n; i++) {pre[i] = pre[i - 1] + nums[i - 1];//下标映射,因为我的pre[0]是虚拟节点if (hash.containsKey(pre[i] - k)){count += hash.get(pre[i] - k);}hash.put(pre[i],hash.getOrDefault(pre[i],0) + 1);//键为前缀和的值 ,值为出现的次数}return count;}滚动数组优化形成前缀和
//因为上述我们只使用了,pre[i - 1] 和 pre[i] 这两种状态,所以可以使用滚动数组进行优化,设置两个变量即可//也就是我们熟知的前缀和public int subarraySum1(int[] nums, int k) {int count = 0;//统计出现了多少次int n = nums.length;HashMap < Integer, Integer > hash = new HashMap<>();//当词典使用,存储所有前缀和int pre = 0;hash.put(0,1);//记录0出现了1次,防止前缀和单独构成答案for (int i = 0; i < n; i++) {pre += nums[i];if (hash.containsKey(pre - k)){count += hash.get(pre - k);}hash.put(pre,hash.getOrDefault(pre,0) + 1);//键为前缀和的值 ,值为出现的次数}return count;}4.乘积为k的最大子数组
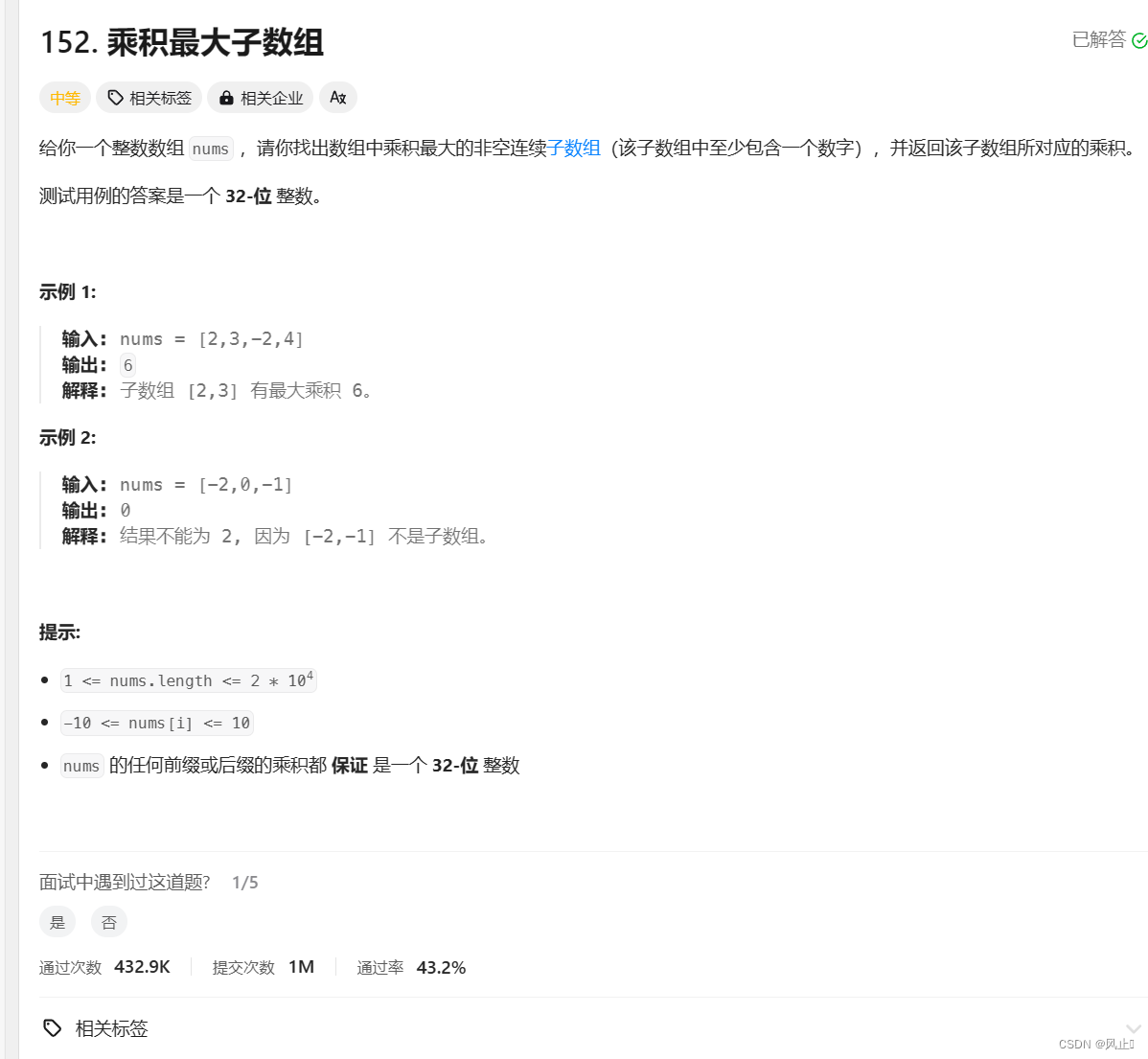
. - 力扣(LeetCode)
思路分析:注释都有明确标注状态表示和转移方程
public int maxProduct(int[] nums) {int n = nums.length;//1.定义状态表示int[] f = new int[n + 1];//以i位置为结尾 所有子数组中 乘积的最大值 遇到正数我要你int[] g = new int[n + 1];//以i位置为结尾 所有子数组中 乘积的最小值 遇到负数我要你//2.状态转移方程 遇到正数我要最大值(f[i - 1]) 遇到负数我要最小值(g[i - 1])//3.初始化 防止i - 1越界但不可保存0,因为初始化的初衷就是保证后续的位置不受影响f[0] = g[0] = 1;//注意多次赋值是从右往左进行的int ret = -0x3f3f3f3f;for (int i = 1; i <= n; i++) {if (nums[i - 1] > 0){f[i] = Math.max(f[i - 1] * nums[i - 1],nums[i - 1]);g[i] = Math.min(g[i - 1] * nums[i - 1],nums[i - 1]);}else {f[i] = Math.max(g[i - 1] * nums[i - 1],nums[i - 1]);g[i] = Math.min(f[i - 1] * nums[i - 1],nums[i - 1]);}ret = Math.max(ret,f[i]);}return ret;}5.乘积为正数的最长子数组长度

. - 力扣(LeetCode)
public int getMaxLen(int[] nums) {int n = nums.length;int ret = 0;//统计//1.状态表示int[] f = new int[n + 1];//以i位置为结尾中的 所有子数组中的 乘积为正数的最大长度int[] g = new int[n + 1];//以i位置为结尾中的 所有子数组中的 乘积为负数的最大长度//2.状态转移方程 f[i]如果i位置为正数为 f[i - 1] + 1 负数 g[i - 1] + 1// g[i]同理正数g[i - 1] + 1 负数 f[i - 1] + 1//3.初始化 默认长度为0不影响后续结果for (int i = 1; i <= n; i++) {if (nums[i - 1] > 0){f[i] = f[i - 1] + 1;//当最后一个元素为正数的时候,并且g[i - 1] = 0表示前面没有负数,所以不可能组成负数g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if (nums[i - 1] < 0){//当最后一个元素为负数的时候,并且g[i - 1] = 0表示前面没有负数,所以不可能组成正数f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}else {//处理为0的情况f[i] = 0;g[i] = 0;}ret = Math.max(ret,f[i]);}return ret;}总结
当解决子数组问题时,动态规划是一个强大而智能的工具。通过将问题分解成更小的子问题并以递归的方式解决它们,动态规划可以高效地找到原始问题的解。在动态规划中,我们常常会遇到两种状态:一种是单独成一段,另一种是以 i 结尾的子数组。
枚举和动态规划是解决子数组问题的两种主要方法。枚举法需要考虑所有可能的子数组组合,然后比较它们以找到最优解。而动态规划则通过保存历史记录来避免不必要的重复计算,从而提高效率。
在动态规划中,常用的技巧包括前缀和和预处理。前缀和可以帮助我们快速求出数组中任意子数组的和,而预处理则可以在问题出现之前就对数据进行处理,以提高计算效率。
综上所述,动态规划是解决子数组问题的一种强大工具,通过合理利用枚举、动态规划、前缀和和预处理等技巧,我们可以高效地解决各种复杂的算法挑战,为问题提供简单明了的解决方案。
相关文章:

对于子数组问题的动态规划
前言 先讲讲我对于这个问题的理解吧 当谈到解决子数组问题时,动态规划(DP)是一个强大的工具,它在处理各种算法挑战时发挥着重要作用。动态规划是一种思想,它通过将问题分解成更小的子问题并以一种递归的方式解决它们,然后利用这些…...
Instal IIS on Windows Server 2022 Datacenter
和以往版本一样,没有什么不同,So easy! WinR - ServerManager.exe 打开服务器管理器,点击【添加角色和功能】,选择自己想要的角色和功能。 一、开始之前:帮助说明,点击【下一步】;…...

飞天使-k8s知识点30-kubernetes安装1.28.0版本-使用containerd方式
文章目录 安装前准备containerd 配置内核参数优化安装nerdctl以上是所有机器全部安装开始安装初始化,这步骤容易出问题! 安装前准备 内核升级包的md5,本人已验证,只要是这个md5值,放心升级 1ea91ea41eedb35c5da12fe7030f4347 ke…...

Oracle 误操作insert delete update 数据回滚
查询回滚数据 select * from tablename AS OF TIMESTAMP TO_TIMESTAMP(2023-12-29 10:29:00,yyyy-mm-dd hh24:mi:ss) where not exists (select 1 from tablename A where A.xh tablename.xh and A.TIME tablename.TIME); TO_TIMESTAMP(2023-12-29 10:29:00,yyyy-mm-dd h…...
Linux系统(CentOS)下安装配置 Nginx 超详细图文教程
一、下载并安装 1.打开nginx官网并点击右侧的download,Nginx官网下载地址 2.选择稳定版本 我放在/usr/local/nginx/下,新建文件夹 mkdir /usr/local/nginx/ 通过xftp传输到Linux的服务器上,这里方法不过多复述。 或者如果Linux联网…...

追求完美用户体验,从变量名设计的细节抓起
在一个安静的办公室里,卧龙和凤雏正坐在电脑前忙碌地工作着。阳光透过窗户洒在他们的脸上,映照出专注的神情。 “变量命名让人摸不着头脑,光看变量名很难搞清楚它的用途。”卧龙眉头紧皱,表情严肃地说道。 “哦?具体是…...

matlab实现K均值聚类
在MATLAB中实现聚类分析,可以使用MATLAB内置的聚类函数,如kmeans(用于K均值聚类),linkage和cluster(用于层次聚类),或者使用MATLAB的统计和机器学习工具箱中的其他函数。 以下是一个…...
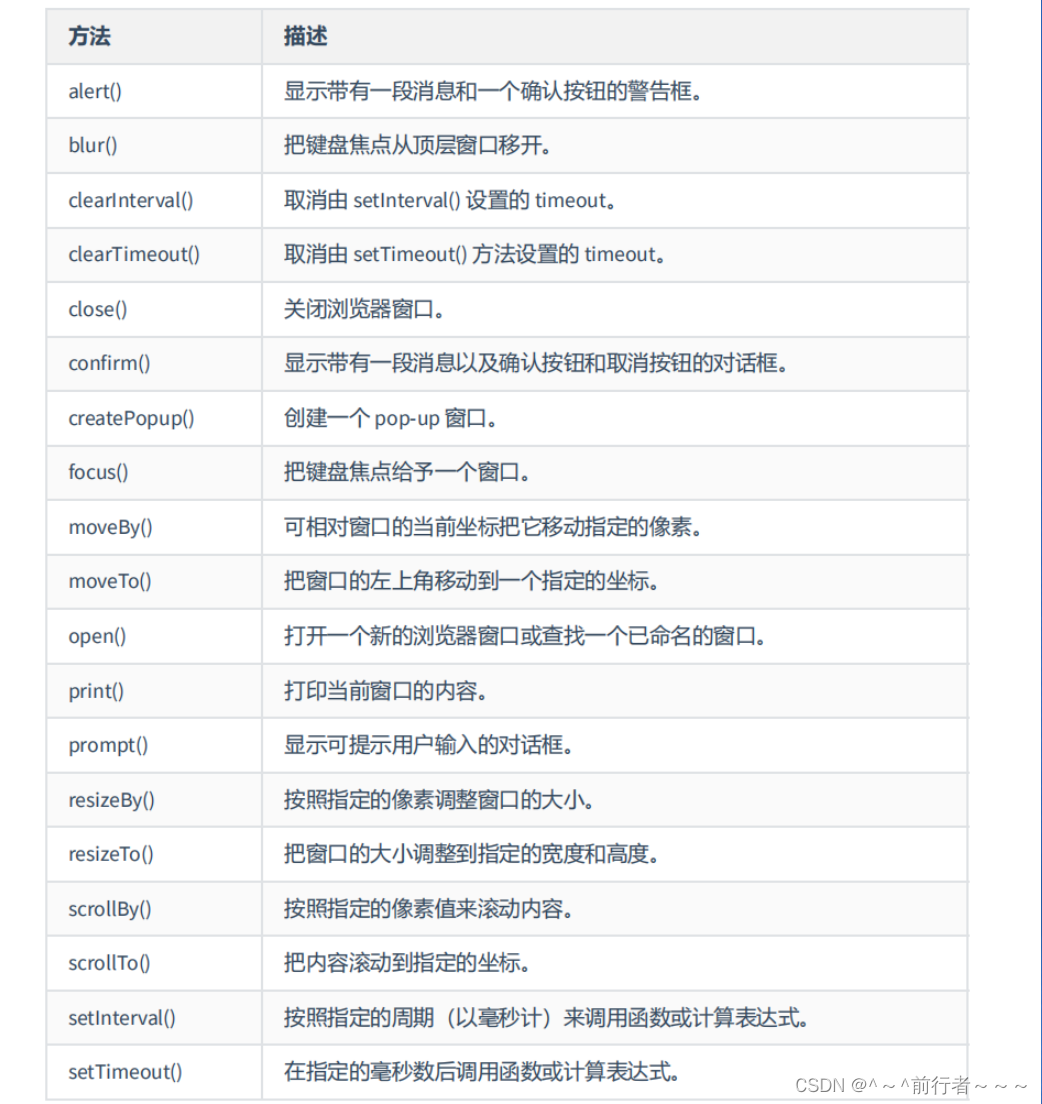
详解BOM编程
华子目录 BOM编程window对象常见的window对象的属性常见的window对象的方法注意 history对象history对象的属性history对象的方法 screen 对象navigator 对象属性方法 location对象属性方法示例 BOM编程 JavaScript本质是在浏览器中运行,所以JavaScript提供了BOM&a…...

情感分类学习笔记(1)
文本情感分类(二):深度学习模型 - 科学空间|Scientific Spaces 一、代码理解 cw lambda x: list(jieba.cut(x)) #定义分词函数 您给出的代码定义了一个使用 jieba 分词库的分词函数。jieba 是一个用于中文分词的 Python 库。该函数 cw 是…...

EtherCAT运动控制器Delta机械手应用
ZMC406硬件介绍 ZMC406是正运动推出的一款多轴高性能EtherCAT总线运动控制器,具有EtherCAT、EtherNET、RS232、CAN和U盘等通讯接口,ZMC系列运动控制器可应用于各种需要脱机或联机运行的场合。 ZMC406支持6轴运动控制,最多可扩展至32轴&#…...

物联网杀虫灯—新型的环保杀虫设备
型号推荐:云境天合TH-FD2S】物联网杀虫灯是一种新型环保杀虫设备,其中风吸式太阳能杀虫灯作为其一种特殊类型,展现了独特的工作原理和优势。 风吸式太阳能杀虫灯以太阳能电池板为电源,白天储存电源,晚上为杀虫灯提供电…...

加盟零食店的真是大冤种
关注卢松松,会经常给你分享一些我的经验和观点。 我一朋友,在老家县城去年失业没事干,手里有一点钱但不多,就想着自己干点啥 。最后经多方打听考察,加盟了一个零食店,前前后后花去了近五六十万,…...

力扣刷题--数组--第三天
今天再做两道二分查找的题目,关于二分查找的知识可看我前两篇博客。话不多说,直接开干! 题目1:69.x 的平方根 题目详情: 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。由于返回类型是整数&#…...
开源即时通讯IM框架 MobileIMSDK v6.5 发布
一、更新内容简介 本次更新为次要版本更新,进行了bug修复和优化升级(更新历史详见:码云 Release Notes、Github Release Notes)。 MobileIMSDK 可能是市面上唯一同时支持 UDPTCPWebSocket 三种协议的同类开源IM框架。轻量级、高…...

React 第二十七章 Hook useMemo
useMemo 函数可以用于缓存计算结果,以避免不必要的重复计算。 在React的函数组件中,当组件重新渲染时,函数组件内的所有代码都会重新执行。有些计算可能是非常消耗资源的,例如进行复杂的计算或进行网络请求。如果这些计算的结果在…...
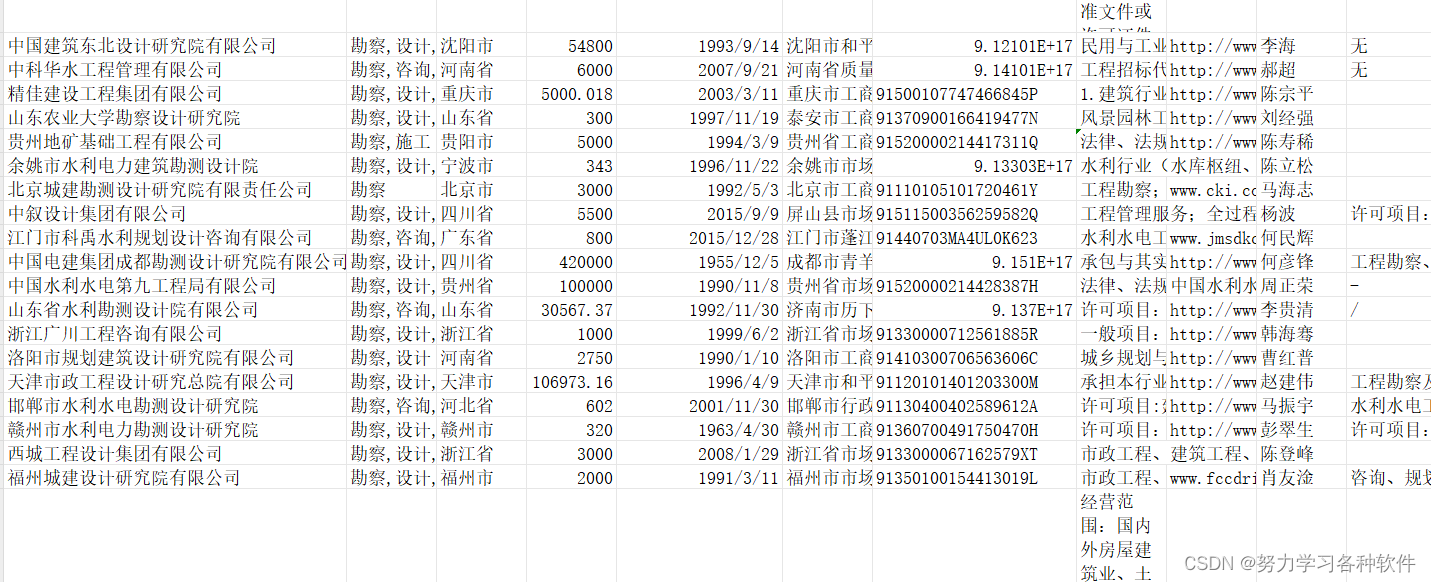
自己写的爬虫小案例
网址:aHR0cDovL2pzc2NqZ3B0Lmp4d3JkLmdvdi5jbi8/dXJsPS92aWV3L3dvcmtpbmdVbml0L3dvcmtpbmdVbml0Lmh0bWw 这串代码能够爬取勘察单位企业的详细信息。 import requests import time import csv f open(勘察单位公司信息.csv,w,encodingutf-8,newline) csv_writer …...

Kafka 环境搭建和使用之单机模式详细教程
上一篇:Kakfa 简介及相关组件介绍 下一篇:Kafka 环境搭建之伪分布式集群详细教程 Kafka 环境搭建 Kafka的环境搭建可以根据不同的需求和场景采取不同的模式,主要包括以下几种: 单机模式(Standalone Mode): 在这种模式下,Kafka、Zookeeper 以及生产者和消费者都在同一…...
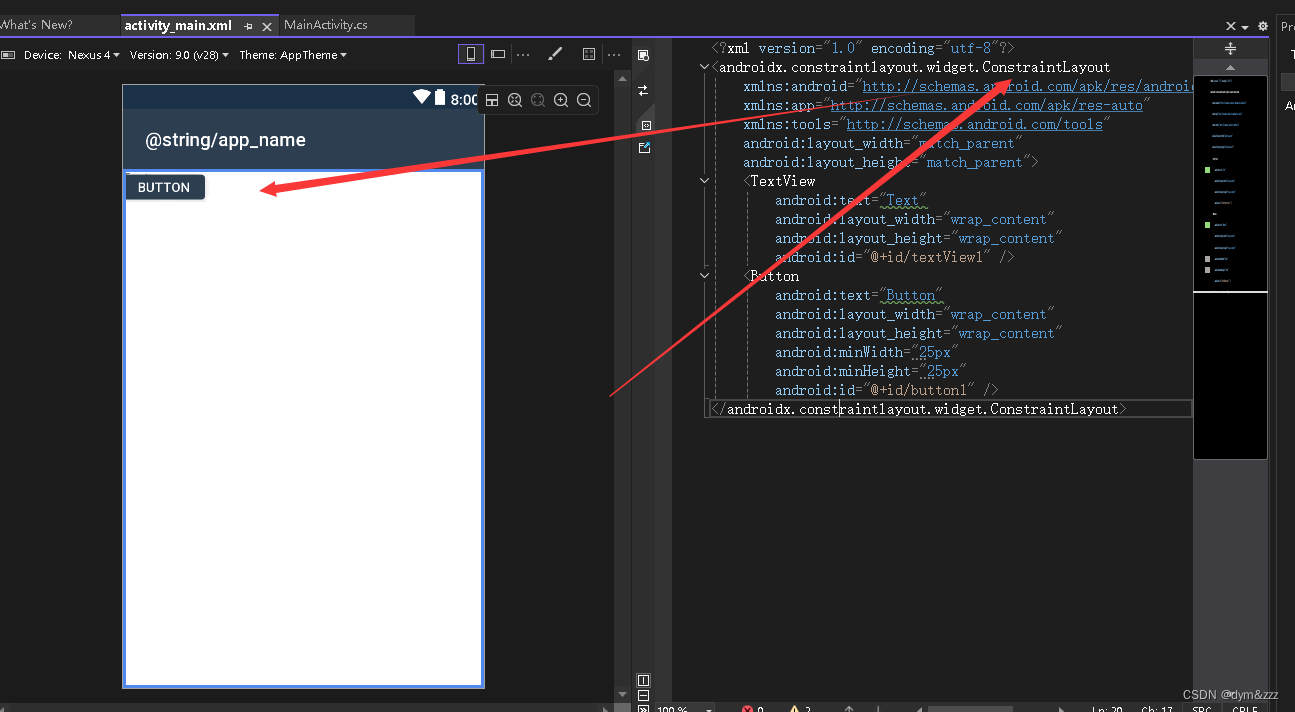
Xamarin.Android项目使用ConstraintLayout约束布局
Xamarin.AndroidX.ConstraintLayout Xamarin.Android.Support.Constraint.Layout Xamarin.AndroidX.ConstraintLayout.Solver Xamarin.AndroidX.DataBinding.ViewBinding Xamarin.AndroidX.Legacy.Support.Core.UI Xamarin.AndroidX.Lifecycle.LiveData ![在这里插入图片描述]…...

探索Java 18:未来技术趋势与革新之路
Java,作为一门历史悠久而又历久弥新的编程语言,始终站在技术发展的前沿,引领着软件开发的潮流。随着Java 18的发布,我们再次见证了这门语言的自我迭代与革新。本文将深入探讨Java 18带来的新特性、技术趋势,以及它如何…...

毕业论文怎么写? 推荐4个AI工具
写作这件事一直让我们从小学时期就开始头痛,初高中时期800字的作文让我们焦头烂额,一篇作文里用尽了口水话,拼拼凑凑才勉强完成。 大学时期以为可以轻松顺利毕业,结果毕业前的最后一道坎拦住我们的是毕业论文,这玩意不…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...