算法--动态规划
动态规划(Dynamic Programming, DP)是一种算法设计技巧,用于解决具有重叠子问题和最优子结构性质的问题。通过将原问题分解为相对简单的子问题的方式来求解复杂问题,动态规划避免了计算重复子问题,从而提高了算法的效率。
动态规划的关键特点包括:
- 重叠子问题:在求解过程中,相同的子问题会被多次计算。动态规划通过存储这些子问题的解(通常是在一个表格中),每个子问题只解决一次,以避免不必要的计算。
- 最优子结构:一个问题的最优解包含其子问题的最优解。这意味着可以通过组合子问题的最优解来构造原问题的最优解。
- 状态转移方程:动态规划算法的核心,它描述了问题的状态如何从一个状态转移到另一个状态。状态转移方程通常取决于当前决策和相应的子问题解。
动态规划的步骤通常包括:
- 定义状态:确定问题的状态,以及状态之间的关系。
- 确定状态转移方程:找出状态之间如何转移的规则。
- 初始化条件:确定初始状态的值。
- 计算顺序:确定计算状态的顺序,确保在计算当前状态时,所需的子状态已经计算过。
- 构造最优解:根据计算出的状态值,构造问题的最优解。
动态规划广泛应用于各种领域,包括但不限于:
- 最短路径问题:如Dijkstra算法和Floyd-Warshall算法。
- 序列对齐问题:如生物信息学中的序列对齐。
- 资源分配问题:如背包问题。
- 字符串编辑距离:如计算两个字符串之间的最小编辑距离。
- 最长公共子序列:找出两个序列共有的最长子序列。
动态规划是解决优化问题的强大工具,但它要求问题具有重叠子问题和最优子结构的特性。正确识别和定义这些特性是应用动态规划成功的关键。
0-1背包问题
0-1背包问题是动态规划中的经典问题。给定一组物品,每种物品都有自己的重量和价值,在限定的总重量内,选择其中若干个(也即每种物品可以选择0个或1个),设计选择方案使得物品的总价值最高。
以下是使用动态规划解决0-1背包问题的C语言实现:
#include <stdio.h>
#include <stdlib.h>// 返回两个整数中的最大值
int max(int a, int b) {return (a > b) ? a : b;
}// 动态规划解决0-1背包问题
// 参数:W为背包最大容量,wt为物品重量数组,val为物品价值数组,n为物品数量
int knapSack(int W, int wt[], int val[], int n) {int i, w;// 创建一个二维数组dp,其中dp[i][w]表示在前i个物品中,能够装入容量为w的背包中的最大价值int **dp = (int **)malloc((n + 1) * sizeof(int *));for (i = 0; i <= n; i++) {dp[i] = (int *)malloc((W + 1) * sizeof(int));}// 填充表格for (i = 0; i <= n; i++) {for (w = 0; w <= W; w++) {if (i == 0 || w == 0)dp[i][w] = 0;else if (wt[i - 1] <= w)dp[i][w] = max(val[i - 1] + dp[i - 1][w - wt[i - 1]], dp[i - 1][w]);elsedp[i][w] = dp[i - 1][w];}}// 存储结果int result = dp[n][W];// 释放dp数组for (i = 0; i <= n; i++) {free(dp[i]);}free(dp);return result;
}// 测试代码
int main() {int val[] = {60, 100, 120};int wt[] = {10, 20, 30};int W = 50;int n = sizeof(val) / sizeof(val[0]);printf("背包中物品的最大价值为:%d", knapSack(W, wt, val, n));return 0;
}
这段代码首先定义了一个max函数,用于返回两个整数中的最大值。knapSack函数是动态规划解决0-1背包问题的核心,它创建了一个二维数组dp,其中dp[i][w]表示在前i个物品中,能够装入容量为w的背包中的最大价值。通过填充这个表格,最终在dp[n][W]中得到了在给定物品和背包容量限制下的最大价值。最后,函数释放了dp数组所占用的内存,并返回了最大价值结果。
最长公共子序列问题
最长公共子序列(Longest Common Subsequence, LCS)问题是寻找两个序列共有的最长子序列的长度,这个子序列不需要在原序列中是连续的。以下是使用动态规划解决最长公共子序列问题的C语言实现:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>// 返回两个整数中的最大值
int max(int a, int b) {return (a > b) ? a : b;
}// 动态规划解决LCS问题
int lcs(char *X, char *Y, int m, int n) {int L[m+1][n+1];int i, j;// 构建L[m+1][n+1],以便保存LCS的长度for (i = 0; i <= m; i++) {for (j = 0; j <= n; j++) {if (i == 0 || j == 0)L[i][j] = 0;else if (X[i-1] == Y[j-1])L[i][j] = L[i-1][j-1] + 1;elseL[i][j] = max(L[i-1][j], L[i][j-1]);}}// L[m][n]包含了X[0..m-1]和Y[0..n-1]的LCS的长度return L[m][n];
}// 打印LCS,这是一个辅助函数
void printLCS(char *X, char *Y, int m, int n) {int index = lcs(X, Y, m, n);char lcs[index+1];lcs[index] = '\0'; // 设置字符串的终止符int i = m, j = n;while (i > 0 && j > 0) {if (X[i-1] == Y[j-1]) {lcs[index-1] = X[i-1]; // 如果当前字符在LCS中i--; j--; index--; // 减少值}else if (L[i-1][j] > L[i][j-1])i--;elsej--;}// 打印LCSprintf("LCS of %s and %s is %s\n", X, Y, lcs);
}// 测试代码
int main() {char X[] = "AGGTAB";char Y[] = "GXTXAYB";int m = strlen(X);int n = strlen(Y);printf("Length of LCS is %d\n", lcs(X, Y, m, n));// 如果需要打印LCS,取消注释下面的行// printLCS(X, Y, m, n);return 0;
}
这段代码首先定义了一个max函数,用于返回两个整数中的最大值。lcs函数是动态规划解决LCS问题的核心,它创建了一个二维数组L,其中L[i][j]表示字符串X[0…i-1]和Y[0…j-1]的LCS的长度。通过填充这个表格,最终在L[m][n]中得到了两个字符串的LCS的长度。
请注意,上述代码中的printLCS函数用于打印LCS,但由于它依赖于L数组,而L数组在lcs函数中是局部变量,直接使用printLCS函数可能会导致编译错误。为了使printLCS函数正常工作,需要对代码进行适当的修改,以便能够访问或重新计算L数组的值。这里提供的printLCS函数主要是为了展示如何根据L数组回溯找到LCS,实际使用时需要注意这一点。
相关文章:

算法--动态规划
动态规划(Dynamic Programming, DP)是一种算法设计技巧,用于解决具有重叠子问题和最优子结构性质的问题。通过将原问题分解为相对简单的子问题的方式来求解复杂问题,动态规划避免了计算重复子问题,从而提高了算法的效率…...
Python基础详解一
一,print打印 print("hello word") print(hello word) 双引号和单引号都可以 二,数据类型 Python中常用的有6种值的类型 输出类型信息 print(type(11)) print(type("22")) print(type(22.2)) <class int> <class str&…...
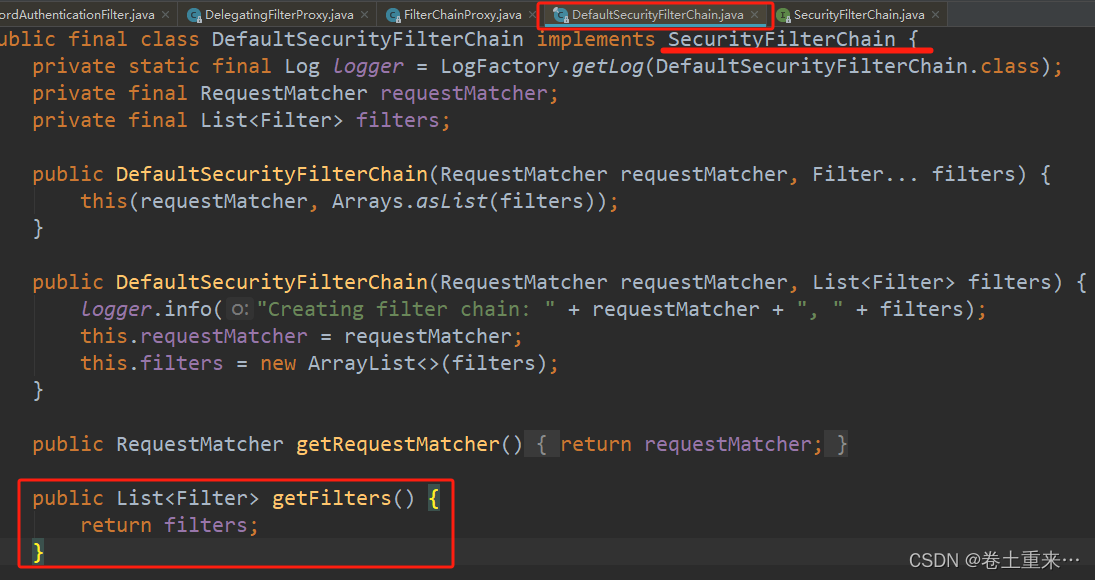
3.SpringSecurity基本原理
SpringSecurity本质是一个过滤器链。十多个过滤器构成一个过滤器链。 这些过滤器在项目启动就会进行加载。每个过滤器执行放行操作才会执行下一个过滤器。 常见过滤器 FilterSecurityInterceptor 是一个方法级的权限过滤器,基本位于过滤器链的最底部。 Excepti…...
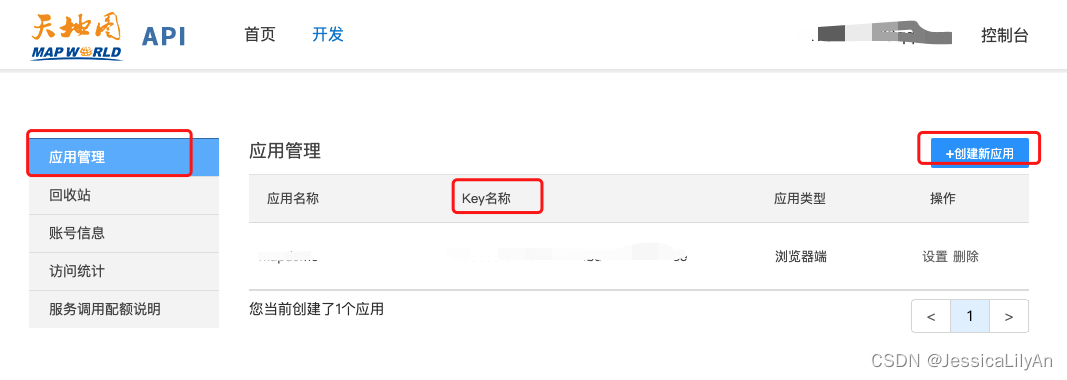
Cesium--加载天地图
背景:vue-admin-temlate cesium 天地图 天地图地址:国家地理信息公共服务平台 天地图 步骤一:申请成为天地图开发者,创建应用 1,天地图使用方法(点击开发资源即可看到此页面) 2,点击控制台-登录账号 …...
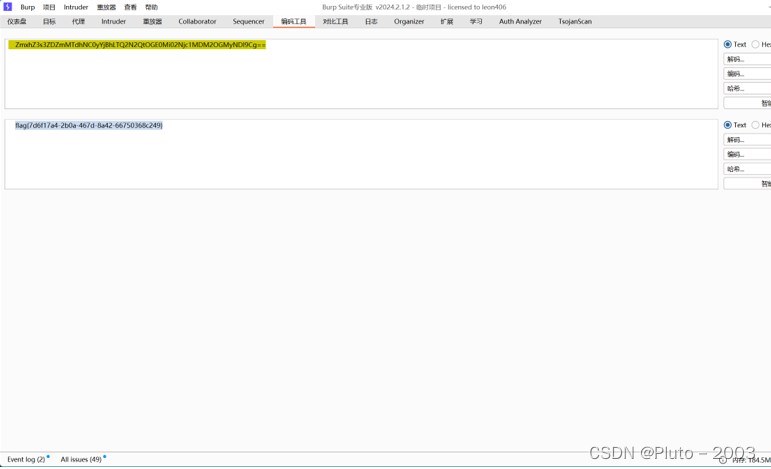
2024蓝桥杯CTF writeUP--packet
根据流量分析,我们可以知道129是攻击机,128被留了php后门,129通过get请求来获得数据 129请求ls Respons在这 里面有flag文件 这里请求打开flag文件,并以base64编码流传输回来 获得flag的base64的数据 然后解码 到手...
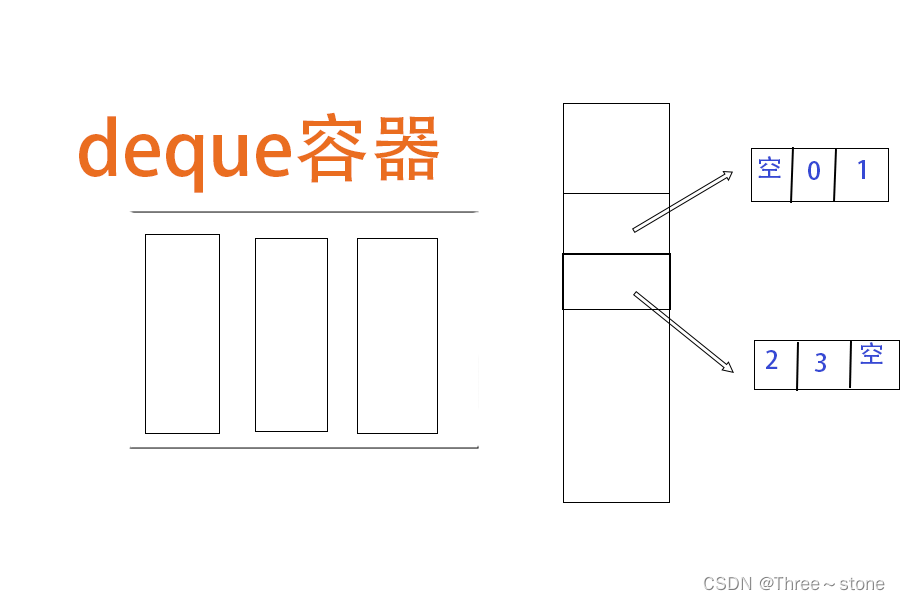
C++容器——deque
deque容器 定义:动态数组,是一种双向开口的线性容器,意味着你不仅可以像在普通队列的末尾添加和移除元素,还可以在前端执行这些操作。 与其他容器相比不同的点: 与vector的主要区别: 连续性:…...
docker-compose安装es+kibana 8.12.2
小伙伴们,你们好,我是老寇,我又回来辣,几个月不见甚是想念啊!!! 因云平台需要改造,es7升级为es8,所以记录一下,es8需要开启ssl认证,需要配置证书…...
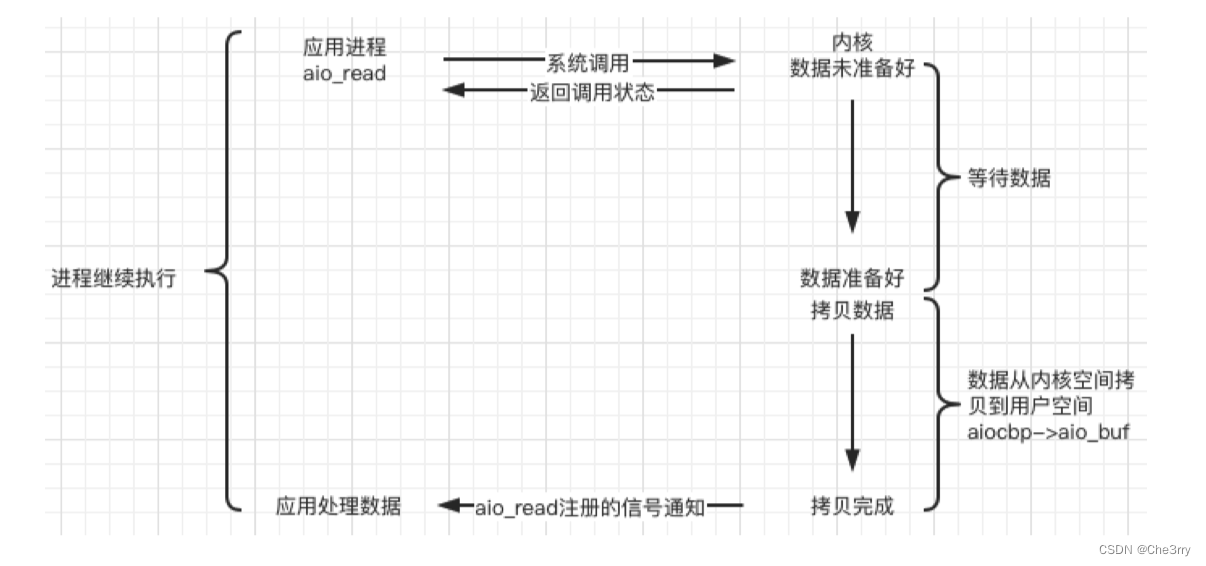
websevere服务器从零搭建到上线(二)|Linux上的五种IO模型
文章目录 阻塞 blocking非阻塞 non-blockingIO复用 IO multiplexing信号驱动 signal-driven异步 asynchronous拓展知识 看过上篇文章英国基本能理解本文五张图的内容websevere服务器从零搭建到上线(一)|阻塞、非阻塞、同步、异步 本文要能够在…...

STM32外设编程指南:GPIO、UART、SPI和I2C
STM32外设编程是嵌入式系统开发中的重要组成部分。以下是对STM32中GPIO(通用输入输出)、UART(通用异步接收传输器)、SPI(串行外设接口)和I2C(互连集成电路)等常见外设的编程指南&…...

git对远程和本地分支进行重命名
要同时对Git的远程和本地分支进行重命名,你需要分几个步骤操作: 重命名本地分支 切换到其他分支:在重命名当前分支之前,确保你不在你想要重命名的那个分支上。你可以通过以下命令切换到另一个分支(比如切换到master分…...

if 语句逻辑判断顺序
C 里面写if语句的时候是按照书写顺序来判断的,不好意思我之前没有考虑过这个问题; 如if(path.back nums[i] && !path.empty()),当path为空时,就会报错,因为编译器先判断的前面的path.back nums[i]࿰…...

第IV章-Ⅱ Vue3中的插槽使用
第IV章-Ⅱ Vue3中的插槽使用 基本插槽默认内容 具名插槽作用域插槽 在 Vue 3 中,插槽(slots)是一种强大的模式,用于将模板代码从父组件注入到子组件中,使得子组件的内容可以在使用时被自定义。Vue 3 中的插槽用法包括基…...

【半个月我拿下了软考证】软件设计师高频考点--系统化教学-网络安全
👨💻 收录于专栏:软件设计师考点暴击 ⭐🅰️进入狂砍分⭐ ⭐软件设计师高频考点文档, ⭐软件设计师高频考点专栏 ⭐软件设计师高频考点⭐ 🎶(A) 考点1,网络攻击 理解记忆 &#…...

E2PROM读写函数
void EEP_write(u8 add,u8 date) {I2CStart();I2CSendByte(0xa0);I2CWaitAck();I2CSendByte(add);I2CWaitAck();I2CSendByte(date);I2CWaitAck();I2CStop();HAL_Delay(5); }这段代码是一个用于向一个I2C设备写入数据的函数。 函数定义: void EEP_write(u8 add,u8 data)这定义…...

MySql中什么是回表? 如何减少回表的次数
背景 在InnerDB中, B数的叶子节点存储数据的索引是聚集索引,也就是我们说的主键索引,而B数的叶子节点存储主键索引的是非聚集索引,也就是其他的索引 普通索引 唯一索引 组合索引,也就是非主键索引,在InnerD…...

【Linux】目录和文件相关的命令,补充:centos7系统目录结构
【Linux】Linux操作系统的设计理念之一就是“一切皆文件”(Everything is a file),即将设备、文件等都当作“文件”处理。 “文件”主要类型有:目录(即文件夹),链接文档(即快捷方式…...

【读点论文】SAM-LIGHTENING: A LIGHTWEIGHT SEGMENT ANYTHING MODEL,改进自注意力机制,然后知识蒸馏提点
SAM-LIGHTENING: A LIGHTWEIGHT SEGMENT ANYTHING MODEL WITH DILATED FLASH ATTENTION TO ACHIEVE 30 ACCELERATION ABSTRACT 分割任意模型(SAM)由于其零样本泛化能力,在分割任务中引起了广泛的关注。然而,SAM在现实世界实践中…...

PostgreSQL函数和运算符
PostgreSQL为内置的数据类型提供了大量的函数和运算符,用户也可以定义自己的函数和运算符,使用psql命令\df和\do可以列出所有可用的函数和运算符 1. 逻辑运算符 常用的逻辑运算符有AND、OR、NOT,逻辑系统有三个值true、fase和nullÿ…...

使用网络工具监控网络性能
网络工具和实用程序有助于有效地检测网络问题,诊断其原因和位置,以及缓解和解决问题,这有助于确保网络环境的稳定性,使用户免受设备连接问题带来的麻烦。 网络工具已经成为每个网络管理员用于有效诊断和处理网络问题的解决方案中…...

Gradle基础笔记
配置镜像 修改 gradle>wrapper>gradle-wrapper.properties distributionUrlhttps://mirrors.aliyun.com/macports/distfiles/gradle/gradle-8.6-all.zip 配置父项目 使用 subprojects 编码问题处理 [compileJava, compileTestJava, javadoc].options.encoding ‘UTF-…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
