SQLite3简单操作
SQLite命令
文章目录
- SQLite命令
- 一、创建数据库
- 二、表的操作
- 1、创建表
- 2、删除表
一、创建数据库
注:使用Ubuntu服务器操作,安装sqlite3
sudo apt update
sudo apt install sqlite3
sqlite3 --version
1、SQLite主要使用命令sqlite3来创建新的数据库
sqlite3 test.db
2、.open test.db 也可以打开数据库文件(如果不存在就新建)
.open test.db
3、.quit 退出数据库
4、附加数据库,绑定数据库文件到其它地方
ATTACH DATABASE 'testDB.db' as 'TEST';
5、分离数据库
DETACH DATABASE 'test.db';
二、表的操作
1、创建表
CREATE TABLE DEPARTMENT(ID INT PRIMARY KEY NOT NULL,DEPT CHAR(50) NOT NULL,EMP_ID INT NOT NULL
);
.table:可以查看自己建立的表
2、删除表
DROP TABLE COMPANY;
相关文章:

SQLite3简单操作
SQLite命令 文章目录 SQLite命令一、创建数据库二、表的操作1、创建表2、删除表 一、创建数据库 注:使用Ubuntu服务器操作,安装sqlite3 sudo apt update sudo apt install sqlite3 sqlite3 --version1、SQLite主要使用命令sqlite3来创建新的数据库 sq…...

从“制造”到“智造”:“灯塔”经验助力中国制造业转型升级-转载
作者:Karel Eloot,侯文皓,Francisco Betti,Enno de Boer和Yves Giraud 作为中国实体经济的主体,制造业是推动中国经济发展乃至全球制造业持续增长的重要引擎。站在历史与未来交汇的新起点上,中国制造业将背…...
——容器操作)
C++ 容器(二)——容器操作
一、容器的修改 容器修改函数 insert():在指定位置插入一个或多个元素erase():删除指定位置或指定范围的元素push_back():将元素添加到容器的末尾pop_back():删除容器的最后一个元素 push_front():将元素添加到容器的开…...

操作系统——进程控制
创建进程 fork fork是一个系统调用函数,用来创建子进程,通过多个执行流完成任务。子进程和父进程共用一份代码,子进程数据使用写时拷贝,即子进程数据在创建的时候和父进程相同,但是当要修改数据的时候,子进…...
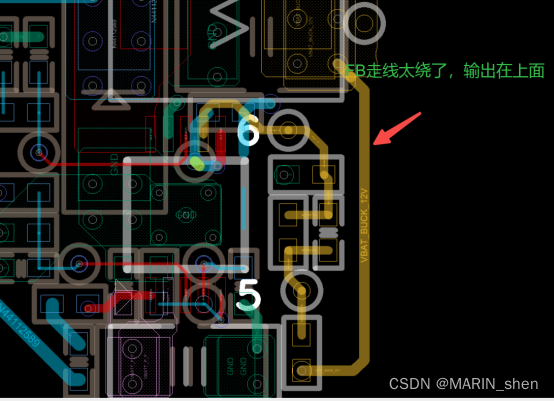
Marin说PCB之国产电源芯片方案 ---STC2620Q
随着小米加入的造车大家庭,让这个本来就卷的要死的造车大家庭更加卷了。随之带来的蝴蝶效应就是江湖上各个造成门派都开始了降本方案的浪潮啊,开始打响价格战了。各家的新能源车企也是不得不开始启动了降本方案的计划了,为了应对降价的浪潮。…...

已解决java.lang.StringIndexOutOfBoundsException: 字符串索引越界异常的正确解决方法,亲测有效!!!
已解决java.lang.StringIndexOutOfBoundsException: 字符串索引越界异常的正确解决方法,亲测有效!!! 目录 问题分析 报错原因 解决思路 解决方法 检查索引范围 检查字符串长度 管理循环中的索引 总结 问题分析 java.lan…...
、@Accessors(chain = true)的作用)
关于实体类注解@Data、@EqualsAndHashCode(callSuper = true)、@Accessors(chain = true)的作用
笔记:都是lombook插件的注解,作用是简化优化代码等,比如getter、setter,一般三者连用能避免一些如继承类的导致的一些坑,比如equal()方法的错误,具体用法可查阅每个注解及属性的作用。 Accessors(chain tr…...

5.9号模拟前端面试10问
5.9号模拟前端面试10问 1.html语义化的理解 HTML语义化是指使用具有明确含义的HTML标签来描述内容,而不仅仅是使用<div>和<span>等通用容器标签。语义化的HTML代码更易于阅读和维护,同时也有助于搜索引擎优化(SEO)。…...

vue3 JSX的使用与警告【JSX 元素隐式具有类型 “any“,因为不存在接口 “JSX.IntrinsicElements“】解决办法
一、安装 pnpm i vitejs/plugin-vue-jsx -D 二、配置 1、tsconfig.json "compilerOptions":{"jsx":"preserve" } 2、vite.config.ts import VueJsx from "vitejs/plugin-vue-jsx"...plugin:[vue(),VueJsx() ] 三、简单使用案例…...
一、计算机基础(Java零基础一)
🌻🌻目录 一、🌻🌻剖析学习Java前的疑问🌻🌻1.1 零基础学习编程1.2 英语不好能学吗?1.3 理解慢能学好吗?1.4 现在学Java晚吗?1.5 Java 和 Python 还有 Go 的选择1.6 Java…...
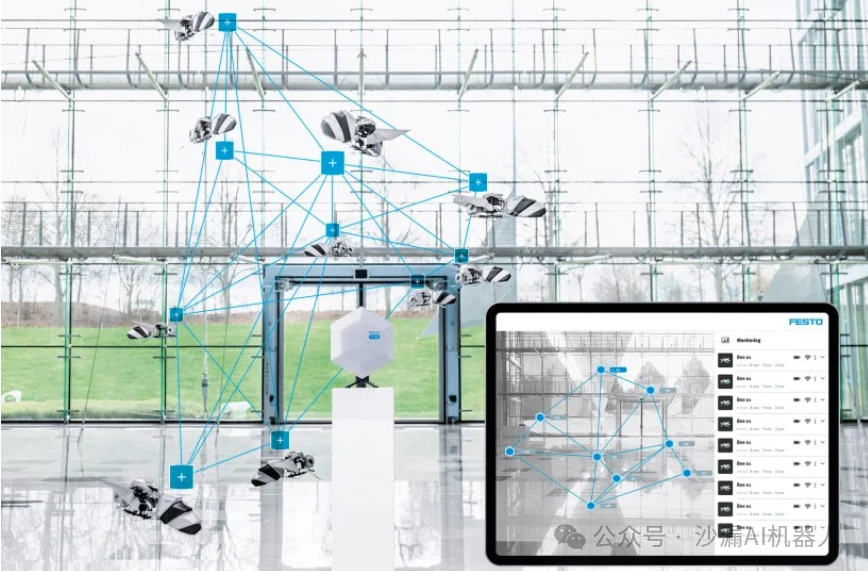
德国著名自动化公司Festo设计了一款仿生蜜蜂,仅重34g,支持多只蜜蜂编队飞行!...
德国著名的气动元件研发及自动化解决方案供应商Festo公司近日展示了一款仿生蜜蜂(BionicBee),重量只有34g,却完全可以实现自主飞行,还支持多只相同的蜜蜂机器人编队飞行。 BionicBee 重约 34 克,长 22 厘米…...

折腾记:C++用开源库Snap7通过S7协议连接西门子PLC
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 不是教程,是避坑指…...
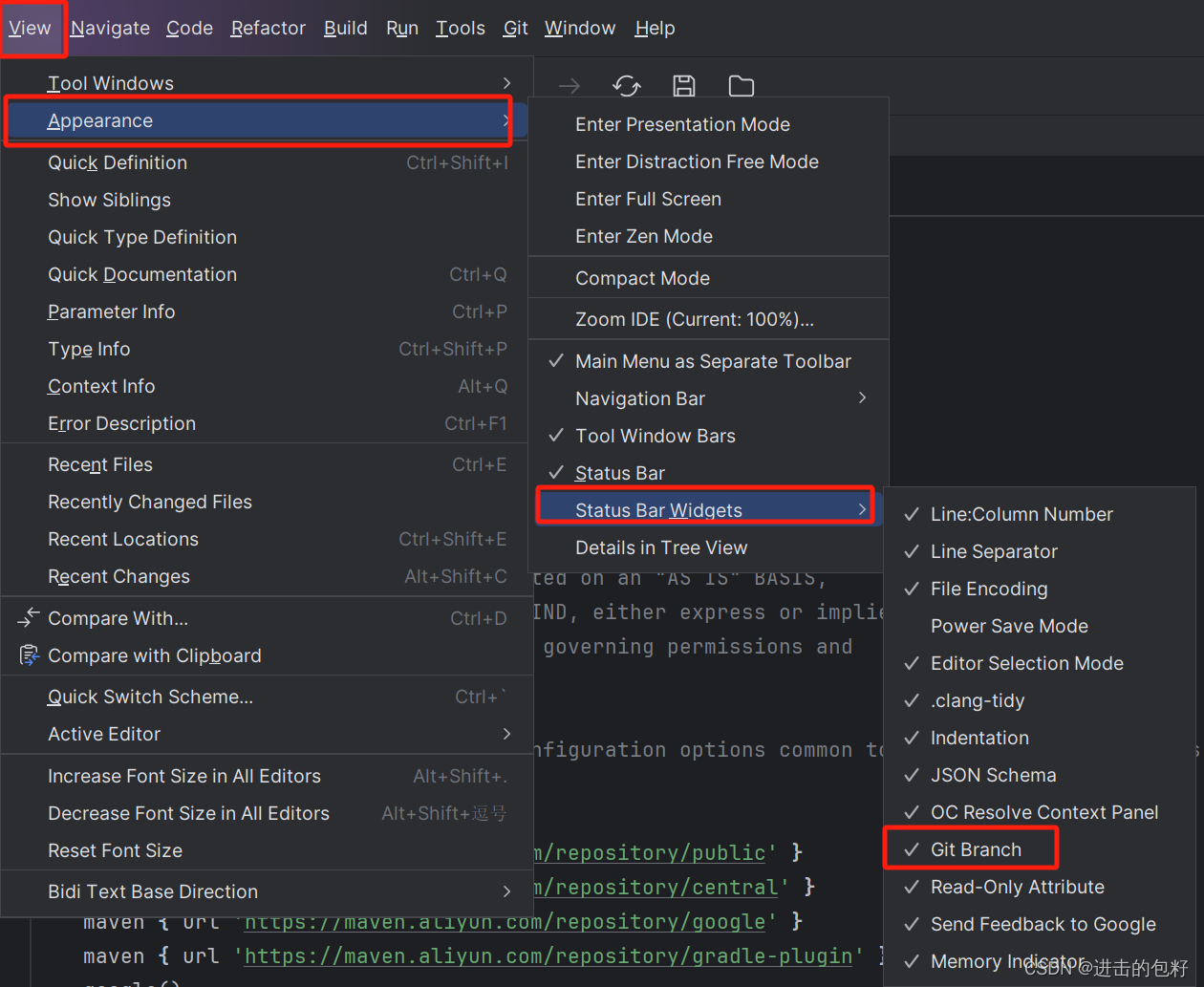
Android studio 新版本 NewUI toolbar显示快捷按钮
新版本的Android studio 启用新的界面,以前许多快捷按键位置有变化 文章目录 设置始终显示主菜单设置ToolBar快捷按钮显示设置右下角显示分支 设置始终显示主菜单 原本要点击左上角几个横向才显示的菜单 设置始终显示,View -> Appearance -> Mai…...

辛普森公式求函数的近似积分【通用计算】
利用辛普森公式可以近似求出复杂函数的积分值,公式如下: ∫ a b f ( x ) d x ≈ h 3 [ y 0 y 2 n − 1 4 ( ∑ i 1 n − 1 y 2 i − 1 ) ∑ i 1 n − 1 y 2 i ] \int_{a}^{b} f(x) dx \approx \frac{h}{3}\left[ y_0 y_{2n-1} 4(\sum\limits_{i1…...

即插即用 | YOLOv8热力图可视化方法详解,揭秘AI如何「看」世界!【附完整源码】
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...
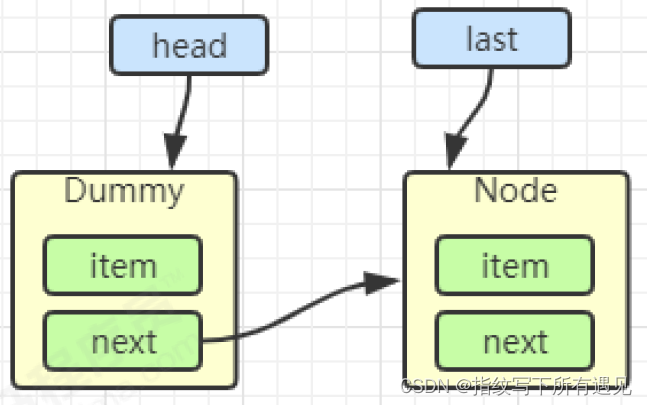
多线程学习D10 收尾了应该
线程安全集合类概述 重点介绍java.util.concurrent.* 下的线程安全集合类,可以发现它们有规律,里面包含三类关键词:Blocking、CopyOnWrite、Concurrent Blocking 大部分实现基于锁,并提供用来阻塞的方法 CopyOnWrite 之类容器修改…...

ai可以做思维导图吗?当然是可以的!
ai可以做思维导图吗?在快节奏的现代生活中,思维导图作为一种高效的信息组织和表达工具,越来越受到人们的青睐。随着人工智能(AI)技术的不断发展,AI思维导图软件也应运而生,它们不仅能够帮助用户…...

景源畅信数字:抖音小店的入住门槛大不大?
近年来,随着短视频平台的崛起,抖音小店逐渐成为了众多商家和创业者关注的焦点。那么,抖音小店的入住门槛究竟大不大呢?本文将从四个方面对这一问题进行详细阐述。 一、注册流程 抖音小店的注册流程相对简单,只需按照官方指引完成…...
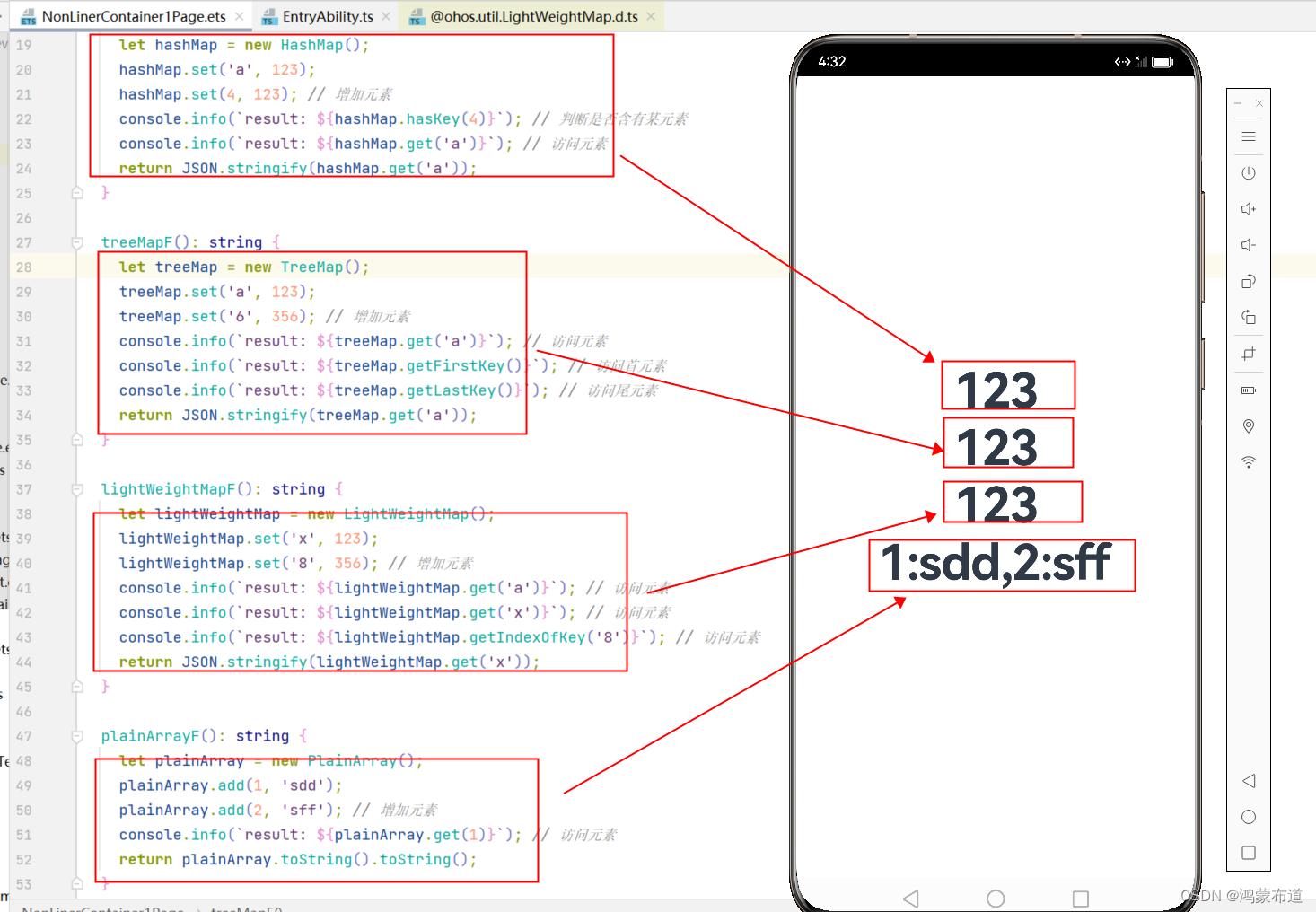
鸿蒙开发-ArkTS语言-容器-非线性容器
鸿蒙开发-UI-web 鸿蒙开发-UI-web-页面 鸿蒙开发-ArkTS语言-基础类库 鸿蒙开发-ArkTS语言-并发 鸿蒙开发-ArkTS语言-并发-案例 鸿蒙开发-ArkTS语言-容器 文章目录 前言 一、非线性容器 1.HashMap 2.HashSet 3.TreeMap 4.TreeSet 5.LightWeightMap 6.LightWeightSet 7.P…...

【C语言】指针篇- 深度解析Sizeof和Strlen:热门面试题探究(5/5)
🌈个人主页:是店小二呀 🌈C语言笔记专栏:C语言笔记 🌈C笔记专栏: C笔记 🌈喜欢的诗句:无人扶我青云志 我自踏雪至山巅 文章目录 一、简单介绍Sizeof和Strlen1.1 Sizeof1.2 Strlen函数1.3 Sie…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
