力扣题目101:对称二叉树
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。
会一些的技术:数据分析、算法、SQL、大数据相关、python
欢迎加入社区:码上找工作
作者专栏每日更新:
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化:企业实战案例
python源码解读
程序员必备的数学知识与应用
备注说明:方便大家阅读,统一使用python,带必要注释,公众号 数据分析螺丝钉 一起打怪升级
题目描述
给定一个二叉树,检查它是否是镜像对称的。
输入格式
- root:二叉树的根节点。
输出格式
- 返回布尔值,表示树是否对称。
示例
示例 1
输入:root = [1,2,2,3,4,4,3]
输出:True
示例 2
输入:root = [1,2,2,null,3,null,3]
输出:False
方法一:递归判断
解题步骤
- 基本情况:如果两个节点都是
None,返回True;一个是None另一个不是,返回False。 - 比较节点:比较当前两节点的值,如果不相等,返回
False。 - 递归比较:递归比较左子树的左孩子和右子树的右孩子,以及左子树的右孩子和右子树的左孩子。
Python 示例
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef isSymmetric(root):"""判断二叉树是否对称:param root: TreeNode, 二叉树的根节点:return: bool, 是否对称"""def isMirror(left, right):if not left and not right:return Trueif not left or not right:return Falsereturn left.val == right.val and isMirror(left.left, right.right) and isMirror(left.right, right.left)return isMirror(root, root)# 示例调用
root = TreeNode(1, TreeNode(2, TreeNode(3), TreeNode(4)), TreeNode(2, TreeNode(4), TreeNode(3)))
print(isSymmetric(root)) # 输出: True
算法分析
- 时间复杂度:(O(n)),其中 (n) 是树中节点的数量,因为需要访问树中的每一个节点。
- 空间复杂度:(O(h)),其中 (h) 是树的高度,空间消耗来自递归的栈空间。
方法二:迭代使用队列
解题步骤
- 初始化队列:将根节点的两份加入队列。
- 迭代比较:每次从队列中取出两个节点并比较它们。
- 子节点入队:如果节点相同,则将它们的子节点按对称顺序加入队列。
Python 示例
from collections import dequedef isSymmetric(root):"""使用队列迭代判断二叉树是否对称:param root: TreeNode, 二叉树的根节点:return: bool, 是否对称"""queue = deque([root, root])while queue:t1, t2 = queue.popleft(), queue.popleft()if not t1 and not t2:continueif not t1 or not t2 or t1.val != t2.val:return Falsequeue.append(t1.left)queue.append(t2.right)queue.append(t1.right)queue.append(t2.left)return True# 示例调用
root = TreeNode(1, TreeNode(2, None, TreeNode(3)), TreeNode(2, None, TreeNode(3)))
print(isSymmetric(root)) # 输出: False
算法分析
- 时间复杂度:(O(n)),因为需要访问每个节点。
- 空间复杂度:(O(n)),在最坏的情况下,队列中需要存储所有节点。
方法三:使用栈进行迭代
解题步骤
- 使用栈:将根节点的两份压入栈中。
- 迭代比较:从栈中弹出两个节点并进行比较。
- 子节点压栈:如果节点相同,则将它们的子节点按对称顺序压入栈中。
Python 示例
def isSymmetric(root):"""使用栈迭代判断二叉树是否对称:param root: TreeNode, 二叉树的根节点:return: bool, 是否对称"""if not root:return Truestack = [(root.left, root.right)]while stack:left, right = stack.pop()if not left and not right:continueif not left or not right or left.val != right.val:return Falsestack.append((left.left, right.right))stack.append((left.right, right.left))return True# 示例调用
root = TreeNode(1, TreeNode(2, None, TreeNode(3)), TreeNode(2, None, TreeNode(3)))
print(isSymmetric(root)) # 输出: False
算法分析
- 时间复杂度:(O(n)),需要访问每个节点。
- 空间复杂度:(O(n)),在最坏的情况下,栈中需要存储所有节点。
不同算法的优劣势对比
| 特征 | 方法一:递归 | 方法二:迭代队列 | 方法三:迭代栈 |
|---|---|---|---|
| 时间复杂度 | (O(n)) | (O(n)) | (O(n)) |
| 空间复杂度 | (O(h)) | (O(n)) | (O(n)) |
| 优势 | 易于实现 | 不使用递归 | 不使用递归 |
| 劣势 | 可能栈溢出 | 空间开销大 | 空间开销大 |
应用示例
这些方法可以用于计算机视觉中对象的对称性检测,软件测试中的树结构数据验证,或者在机器学习数据预处理中检查数据的对称性。
相关文章:

力扣题目101:对称二叉树
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。 会一些的技术:数据分析、算法、SQL、大数据相关、python 欢迎加入社区:码上找工作 作者专栏每日更新: LeetCode解锁1000题: 打怪升级之旅 python数据分析…...
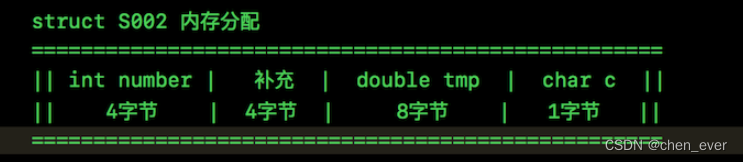
struct和union大小计算规则
Union 一:联合类型的定义 联合也是一种特殊的自定义类型,这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间(所以联合也叫共用体) 比如:共用了 i 这个较大的空间 二: 联合的…...

数据库课程设计《基于Spring Boot + MyBatis + MySQL 实现Java医院药品管理系统》+源代码
文章目录 源代码下载地址项目介绍项目功能 项目备注源代码下载地址 源代码下载地址 点击这里下载源码 项目介绍 项目功能 库存管理 登记入库的药品。 登记出库的药品。 每日检查库存下限,报警。 每日检查过期的药品,报警并做退回销毁处理。 对有问题…...
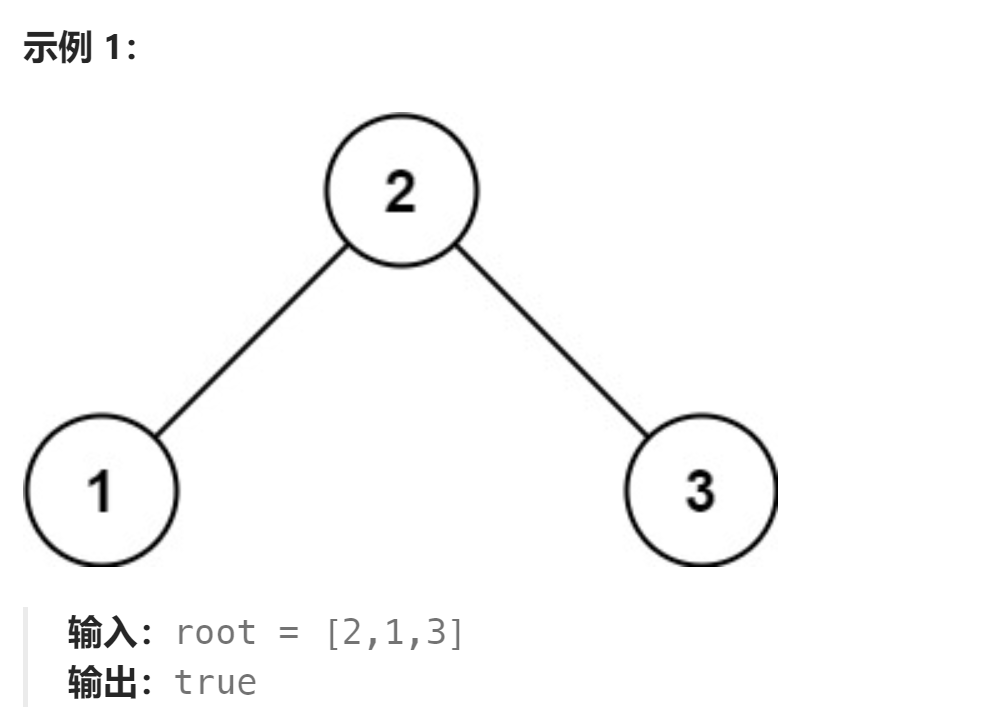
【每日力扣】98. 验证二叉搜索树 与 108. 将有序数组转换为二叉搜索树
🔥 个人主页: 黑洞晓威 😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害 98. 验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下&a…...

Django3 个人开发笔记
查询函数 select_related 在 Django ORM 中,select_related 是一个查询性能优化工具,用于解决关联对象的查询效率问题。当你有两个通过外键(ForeignKey)或一对一字段(OneToOneField)连接的模型时…...
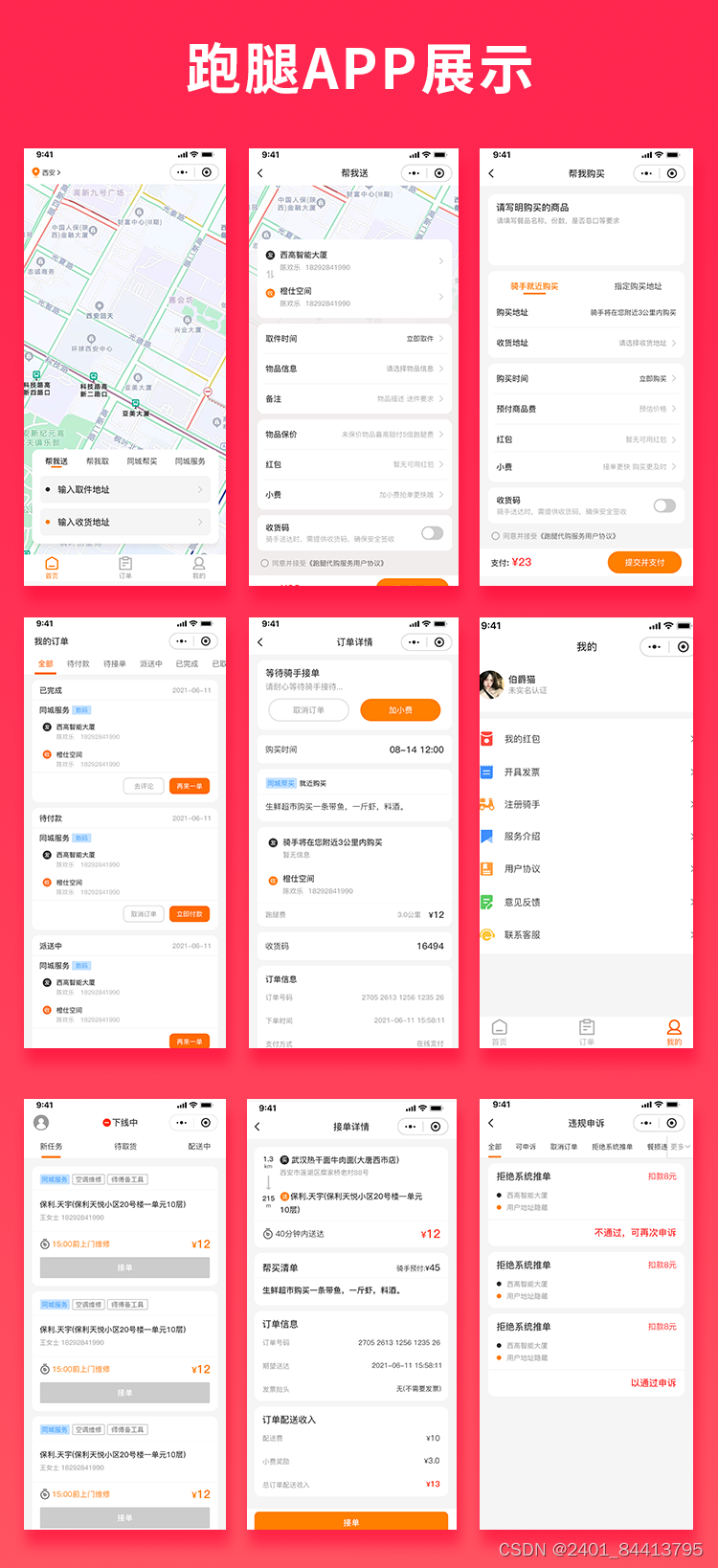
【全开源】Java U U跑腿同城跑腿小程序源码快递代取帮买帮送源码小程序+H 5+公众号跑腿系统
特色功能: 智能定位与路线规划:UU跑腿小程序能够利用定位技术,为用户提供附近的跑腿服务,并自动规划最佳路线,提高配送效率。订单管理:包括订单查询、订单状态更新、订单评价等功能,全行业覆盖…...

物联网实战--平台篇之(五)账户界面
目录 一、界面框架 二、首页(未登录) 三、验证码登录 四、密码登录 五、帐号注册 六、忘记密码 本项目的交流QQ群:701889554 物联网实战--入门篇https://blog.csdn.net/ypp240124016/category_12609773.html 物联网实战--驱动篇https://blog.csdn.net/ypp240124016/cat…...
9. Django Admin后台系统
9. Admin后台系统 Admin后台系统也称为网站后台管理系统, 主要对网站的信息进行管理, 如文字, 图片, 影音和其他日常使用的文件的发布, 更新, 删除等操作, 也包括功能信息的统计和管理, 如用户信息, 订单信息和访客信息等. 简单来说, 它是对网站数据库和文件进行快速操作和管…...

ELK+kafka日志采集
ElasticSeach(存储日志信息) Logstash(搬运工) Kibana 连接ElasticSeach图形化界面查询日志 ELK采集日志的原理: 在每个服务器上安装LogstashLogstash需要配置固定读取某个日志文件Logstash将日志文件格式化为json的…...

【C++ list所有函数举例如何使用】
C 中的 std::list 是一个双向链表,提供了在列表中添加、删除、访问元素等操作的方法。以下是一些常用的 std::list 函数以及如何使用它们的示例: push_back(const T& value): 在列表的末尾添加一个值为 value 的元素。 std::list<int> mylis…...

HTML5(1)
目录 一.HTML5(超文本(链接)标记(标签<>)语言) 1.开发环境(写代码,看效果) 2.vscode 使用 3.谷歌浏览器使用 4.标签语法 5.HTML基本骨架(网页模板) 6.标签的…...

【LAMMPS学习】八、基础知识(6.2)LAMMPS GitHub 教程
8. 基础知识 此部分描述了如何使用 LAMMPS 为用户和开发人员执行各种任务。术语表页面还列出了 MD 术语,以及相应 LAMMPS 手册页的链接。 LAMMPS 源代码分发的 examples 目录中包含的示例输入脚本以及示例脚本页面上突出显示的示例输入脚本还展示了如何设置和运行各…...

专业习惯:避开本地语言,使用通用语言
如果你的目标是走一步看一步,那躺平就得了,学习什么的都没有必要。如果你的目标是远方,那么就需要未雨绸缪。 在工作之中,本地语言及习惯固然可用,但非常局限,随便换一个地方和场景,别人就难以理…...

【Leetcode每日一题】 综合练习 - 逆波兰表达式求值(难度⭐⭐)(73)
1. 题目解析 题目链接:150. 逆波兰表达式求值 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 2.算法原理 数据结构选择: 使用栈(stack<int>)来存储操作数,以便进…...

2G 3G LTE 5G的区别
2G、3G、LTE和5G是不同代的移动通信技术,每一代技术都在其前一代的基础上提供了改进的性能、更高的数据速率和新的功能。以下是这些技术的主要区别: ### 2G (第二代移动通信技术): - **数据速率**:较低的数据速率,通常在几百kbps…...

《21天学通C++》(第二十章)STL映射类(map和multimap)
为什么需要map和multimap: 1.查找高效: 映射类允许通过键快速查找对应的值,这对于需要频繁查找特定元素的场景非常适合。 2.自动排序: 会自动根据键的顺序对元素进行排序 3.多级映射: 映射类可以嵌套使用,创…...

5月游戏市场迎来新的体验,网易两款游戏重磅出炉
易采游戏网5月9日消息,随着科技的飞速发展,手机游戏已经成为人们休闲娱乐的重要方式。在这个领域,网易作为国内领先的游戏开发商,一直致力于为玩家带来高品质的游戏体验。近日,网易携手国际大厂Square Enix,…...
15_Scala面向对象编程_访问权限
文章目录 Scala访问权限1.同类中访问2.同包不同类访问3.不同包访问4.子类权限小结 Scala访问权限 知识点概念 private --同类访问private[包名] --包私有; 同类同包下访问protected --同类,或子类 //同包不能访问(default)(public)默认public --公…...

LeetCode|700. Search in Binary Search Tree
题目 You are given the root of a binary search tree (BST) and an integer val. Find the node in the BST that the node’s value equals val and return the subtree rooted with that node. If such a node does not exist, return null. Example 1: Input: root […...
MacOS下载安装JDK8
一、前言 今天给苹果电脑安装JDK环境,后续打算把Mac系统也用起来,也体验一把用苹果系统开发。 JDK就不过多介绍了,大家都是JAVA开发,JDK就是JAVA开发的必要环境。目前已经更新到JDK20了,不过我是不会更新的࿰…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
