力扣爆刷第133天之动态规划收尾(距离编辑与回文子串)
力扣爆刷第133天之动态规划收尾(距离编辑与回文子串)
文章目录
- 力扣爆刷第133天之动态规划收尾(距离编辑与回文子串)
- 一、72. 编辑距离
- 二、647. 回文子串
- 三、516. 最长回文子序列
一、72. 编辑距离
题目链接:https://leetcode.cn/problems/edit-distance/description/
思路:本题也是前面重复子序列的变体,可以对字符串进行增删替换操作,其中增加和删除是一样的,而替换依赖的是前一个位置。
定义dp[i][j]表示以下标i为结尾的word1和以下标j为结尾的word2要相等所需要的操作。
如果word1[i] == word2[j],那么所需次数依赖于word1[i-1]和word2[j-1],即dp[i][j] = dp[i-1][j-1]。
如果word1[i] != word2[j],那么增删对应的都是dp[i-1][j],dp[i][j-1],替换对应的是dp[i-1][j-1],取三者最低。
class Solution {public int minDistance(String word1, String word2) {int m = word1.length(), n = word2.length();int[][] dp = new int[m+1][n+1];for(int i = 0; i <= m; i++) dp[i][0] = i;for(int i = 0; i <= n; i++) dp[0][i] = i;for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(word1.charAt(i) == word2.charAt(j)) {dp[i+1][j+1] = dp[i][j];}else{dp[i+1][j+1] = Math.min(Math.min(dp[i+1][j], dp[i][j+1]), dp[i][j]) + 1;}}}return dp[m][n];}
}二、647. 回文子串
题目链接:https://leetcode.cn/problems/palindromic-substrings/description/
思路:
常规做法:本题求回文子串的个数,子串是要求连续的,我们可以从单点和双点,向字符串两段遍历,并且记录下子串的个数。
也可以使用动态规划,定义dp[i][j]表示,区间s[i,j]是回文子串,dp[i][j]依赖于dp[i+1][j-1],也就是当前位置的左下方。
class Solution {public int countSubstrings(String s) {int sum = 0;for(int i = 0; i < s.length(); i++) {sum += countSum(s, i, i);sum += countSum(s, i, i+1);}return sum;}int countSum(String s, int i, int j) {int count = 0;while(i >= 0 && j < s.length()) {if(s.charAt(i) == s.charAt(j)) {count++;i--;j++;}else{break;}}return count;}}动态规划解法:
class Solution {public int countSubstrings(String s) {int len = s.length(), sum = 0;boolean[][] dp = new boolean[len][len];for(int i = len-1; i >= 0; i--) {for(int j = i; j < len; j++) {if(s.charAt(i) == s.charAt(j) && (j-i<=2 || dp[i+1][j-1])) {dp[i][j] = true;sum++;}}}return sum;}
}三、516. 最长回文子序列
题目链接:https://leetcode.cn/problems/longest-palindromic-subsequence/
思路:上一题求的是回文子串的个数,本题求的是回文子序列的长度,一个连续一个不连续。定义dp[i][j]表示区间[i, j]中的最长回文子序列的长度是dp[i][j],例如a b b b a的长度依赖于 bbb中回文子序列的长度,所以遍历的方式是从下往下,从左往右。s[i] = s[j]时依赖于左下角的元素dp[i][j] = dp[i+1][j-1],s[i] != s[j]时,就类似于a b b b 或者 b b b a,即dp[i][j] = Math.max(dp[i][j-1], dp[i+1][j]);
class Solution {public int longestPalindromeSubseq(String s) {int len = s.length();int[][] dp = new int[len][len];for(int i = 0; i < len; i++) dp[i][i] = 1;for(int i = len-1; i >= 0; i--) {for(int j = i+1; j < len; j++) {if(s.charAt(i) == s.charAt(j)) {dp[i][j] = dp[i+1][j-1] + 2;}else{dp[i][j] = Math.max(dp[i][j-1], dp[i+1][j]);}}}return dp[0][len-1];}
}相关文章:
)
力扣爆刷第133天之动态规划收尾(距离编辑与回文子串)
力扣爆刷第133天之动态规划收尾(距离编辑与回文子串) 文章目录 力扣爆刷第133天之动态规划收尾(距离编辑与回文子串)一、72. 编辑距离二、647. 回文子串三、516. 最长回文子序列 一、72. 编辑距离 题目链接:https://l…...

List集合中对asList的使用
List<String> sArrays.asList(“qwe”,”cvb”,”mnb”); List<String> s1s.subList(1,2); System.out.Pintln(“s”);//输出结果:[qwe,cvb,mnb] System.out.Pintln(“s1”);//输出结果:[cvb] s1.add(“123qwe”);//报错:java…...

软件测试所有测试方法
β测试_Beta测试 β测试,英文是Beta testing。又称Beta测试,用户验收测试(UAT)。 β测试是软件的多个用户在一个或多个用户的实际使用环境下进行的测试。开发者通常不在测试现场,Beta测试不能由程序员或测试员完成。 …...

linux 下 /usr/local的作用
在Linux系统中,/usr/local目录扮演着特定的角色,它是为用户自安装的软件提供一个标准位置。以下是/usr/local目录的主要用途和特点: 用户级程序目录:该目录用于存放用户自行编译安装的软件或者第三方应用程序,区别于操…...
【web网页制作】html+css旅游家乡河南开封主题网页制作(4页面)【附源码】
HTMLCSS家乡河南主题网页目录 🍔涉及知识🥤写在前面🍧一、网页主题🌳二、页面效果Page1 首页Page2 开封游玩Page 3 开封美食Page4 留言 🌈 三、网页架构与技术3.1 脑海构思3.2 整体布局3.3 技术说明书 🐋四…...

MySQL用命令行导出数据库
问题: 交作业的时候要求交数据文件,因为用的MySQL数据库,就在想怎么用命令行导出数据库,在csdn上找了其他文章,使用MySQL的命令行用下面语句,结果发生报错 mysqldump -u 用户名 -p 数据库名 > 输出地址…...
uniapp video 层级覆盖
层级覆盖 cover-view组件 我这里做了个判断 监听全屏时隐藏按钮 根据项目需求自行更改...
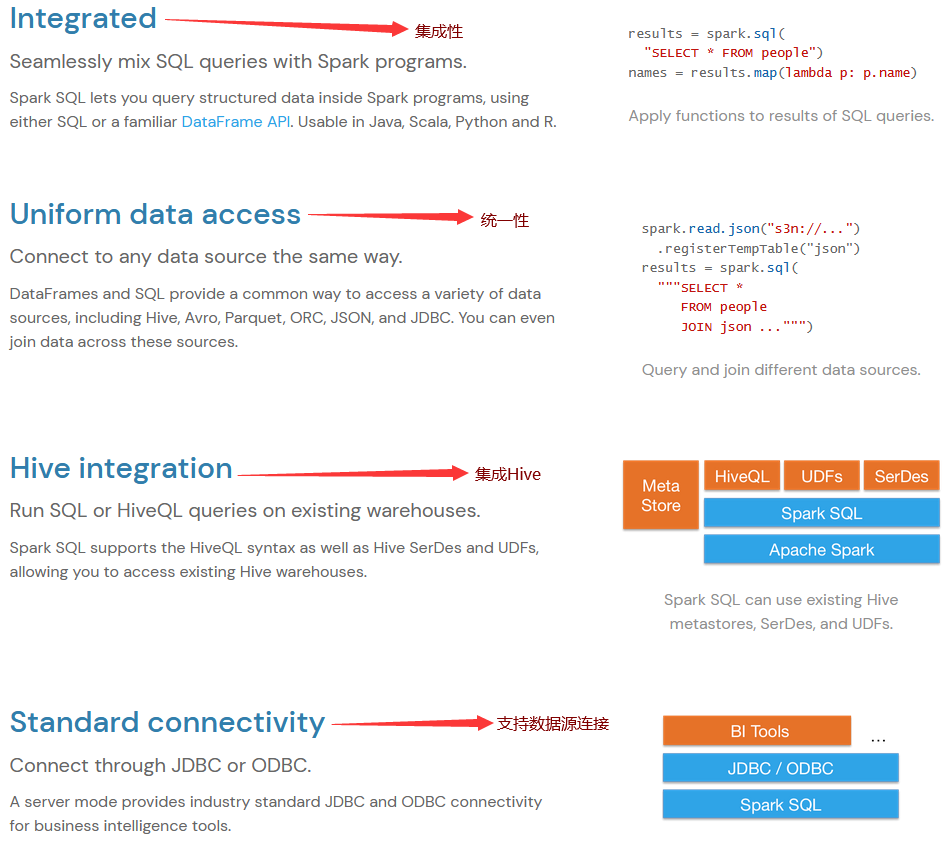
SparkSQL概述
1.1. SparkSQL介绍 SparkSQL,就是Spark生态体系中的构建在SparkCore基础之上的一个基于SQL的计算模块。SparkSQL的前身不叫SparkSQL,而是叫做Shark。最开始的时候底层代码优化、SQL的解析、执行引擎等等完全基于Hive,总是Shark的执行速度要比…...

docker 和 docker-compose
Docker是一种开源的容器化平台,它可以帮助开发人员将应用程序及其所有依赖项打包到一个独立的、可移植的容器中。这意味着您可以在任何地方运行Docker容器,而不需要担心环境差异或依赖项的问题。 Docker Compose是Docker官方提供的一个工具,…...

微信小程序支付(完整版)-ThinkPHP/Uniapp
技术说明 1.前端:uniapp、vue3 2.接口:PHP8、ThinkPHP8、MySQL8.0 3.微信支付- PHP,官方示例文档 4.示例代码的模型及业务自己进行调整,不要一味的复制粘贴!!! 流程说明 1.小程序调用接口…...
同时安装多个nodejs版本可切换使用,或者用nvm管理、切换nodejs版本(两个详细方法)
目录 一.使用nvm的方法: 1.卸载nodejs 2.前往官网下载nvm 3.安装nvm 4.查看安装是否完成 5.配置路径和淘宝镜像 6.查看和安装各个版本的nodejs 7.nvm的常用命令 二.不使用nvm,安装多个版本: 1.安装不同版本的nodejs 2.解压到你想放…...
马化腾用了一年多的时间,告诉所有人,视频号小店是新风口!
大家好,我是电商笨笨熊 当腾讯说出自己要做电商的时候,所有人都在说,根本不可能; 甚至在视频号小店正式推出之后,依旧有人说,腾讯做电商就是笑话; 一个“抄”过来的项目,毫无特色…...

代码随想录算法训练营第36期DAY19
DAY19 104二叉树的最大深度 根节点的高度就是最大深度。 非递归法: /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) …...
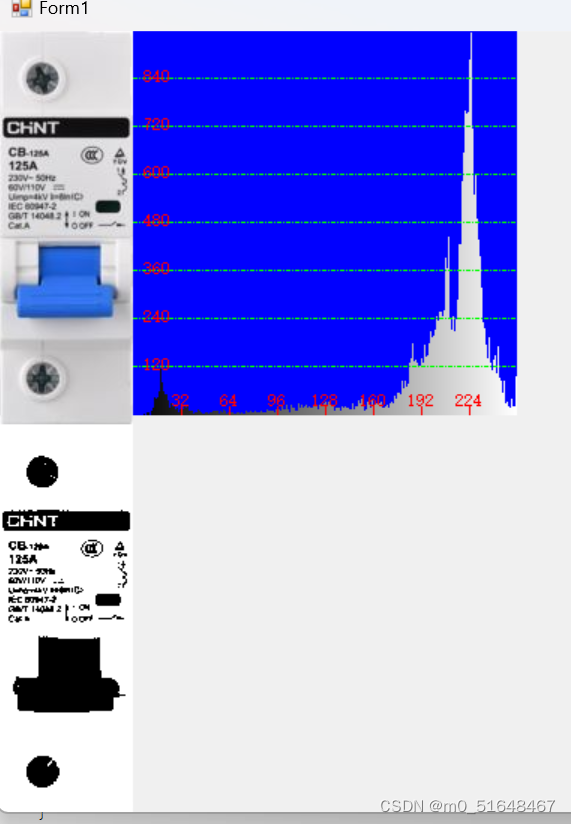
C#图像:1.图像区域分割与提取
(1)创建一个名为SplitImage的窗体的应用程序,将窗体改名为FormSplitImage。 (2)创建一个名为ImageProcessingLibrary的类库程序,为该工程添加名为ImageProcessing的静态类 (3)为Imag…...
炸弹使用技巧
掼蛋掼蛋,打的就是炸弹。炸弹是指掼蛋中由4-8张相同牌点的牌组成的牌型,需要注意的是:每局牌中都有两张红桃的牌型为逢人配,可以配除了大小王以外的任意牌,因此掼蛋中牌数最多的炸弹可以达到10张。 两副扑克牌中&#…...
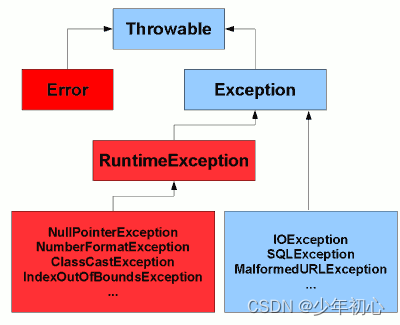
SpringAop详解
文章目录 一、Spring自定义注解1、什么是注解👨🏫2、注解的目的或作用💞3、JDK内置注解💫 【内置元注解 一共八个固定注解】4、元注解 🎯5、自定义注解📸5、Java反射API和类加载过程51、什么是反射基本原…...
对XYctf的一些总结
对XYctf的一些总结 WEB 1.http请求头字段 此次比赛中出现的: X-Forwarded-For/Client-ip:修改来源ip via:修改代理服务器 还有一些常见的字段: GET:此方法用于请求指定的资源。GET请求应该安全且幂等,…...

Visual Studio和Visual Studio Code适用于哪些编程语言
Visual Studio和Visual Studio Code都适用于多种编程语言,它们的适用编程语言如下: Visual Studio适用于: C#Visual Basic .NETF#CJavaScriptTypeScriptPythonHTML/CSSJava(通过插件支持) Visual Studio Code适用于…...
缓存菜品操作
一:问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大。 二:实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: 每个分…...

达梦数据库常用命令整理
1.数据库自身信息 1.1 查询实例信息 SQL> select name inst_name from v$instance;行号 INST_NAME ---------- --------- 1 DMSERVER已用时间: 11.211(毫秒). 执行号:15.1.2 查询数据库当前状态 SQL> select status$ from v$instance;行号 STATUS$ -…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
