C# WinForm —— 12 ListBox绑定数据
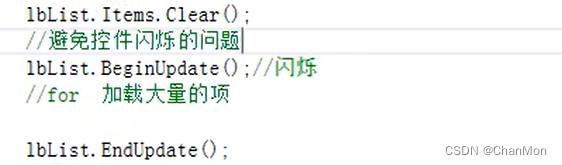
ListBox加载大量数据时,避免窗体闪烁的方法:
在加载语句的前后分别加上 BeginUpdate()方法 和 EndUpdate()方法
指定一个集合为绑定的数据源
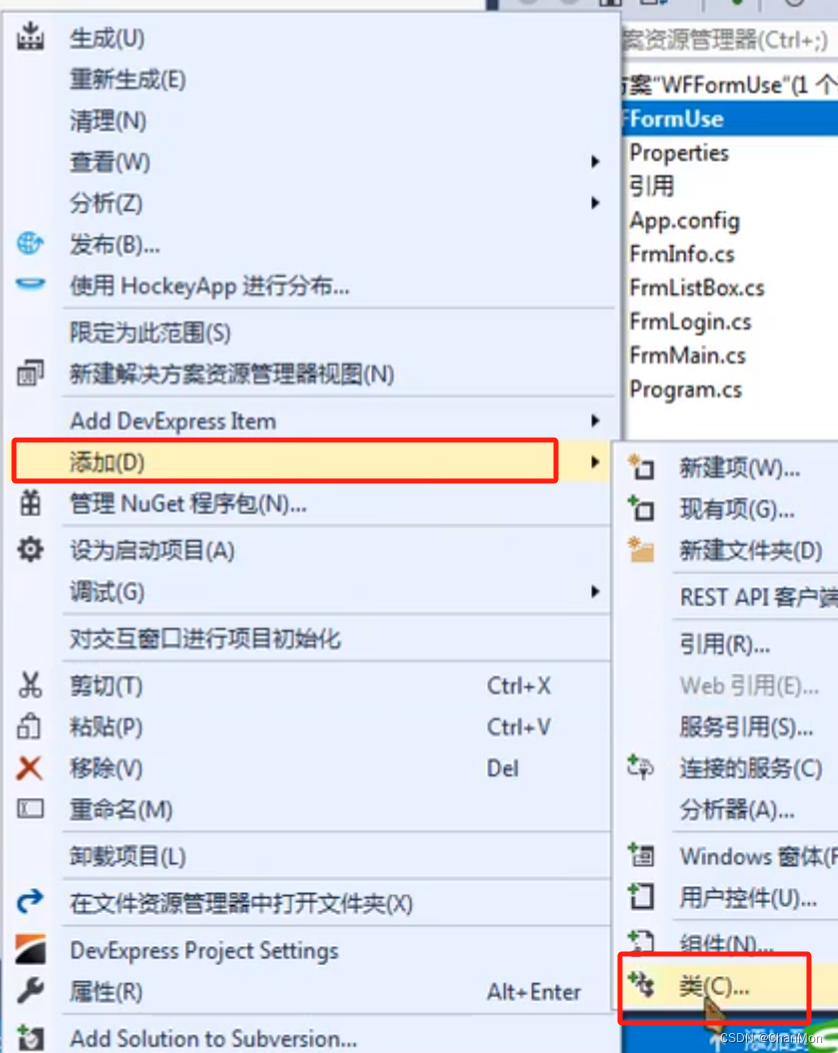
1. 首先,右键项目,添加类
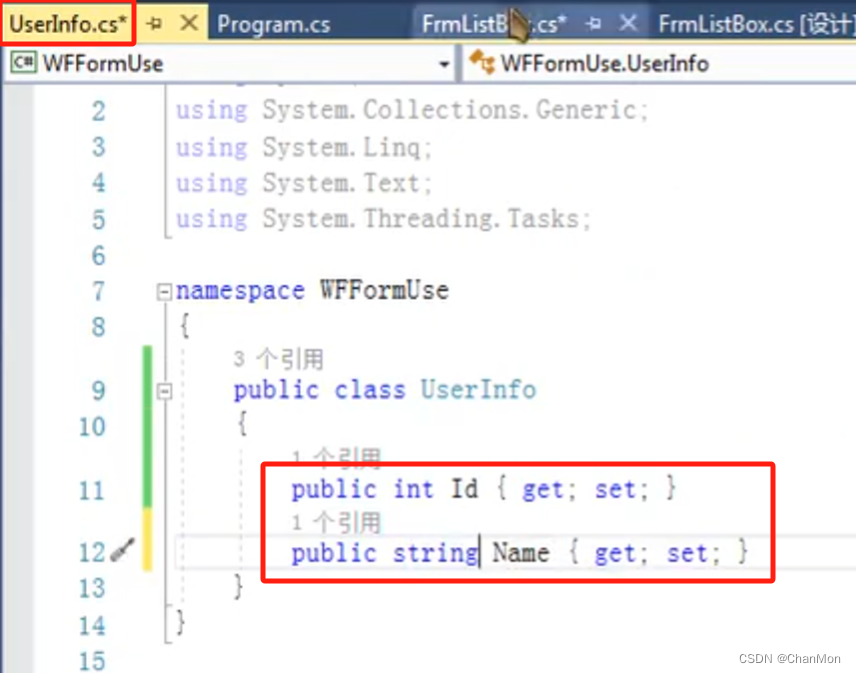
2. 在新建的类文件中添加属性值信息
3. 构建初始化的对象集合
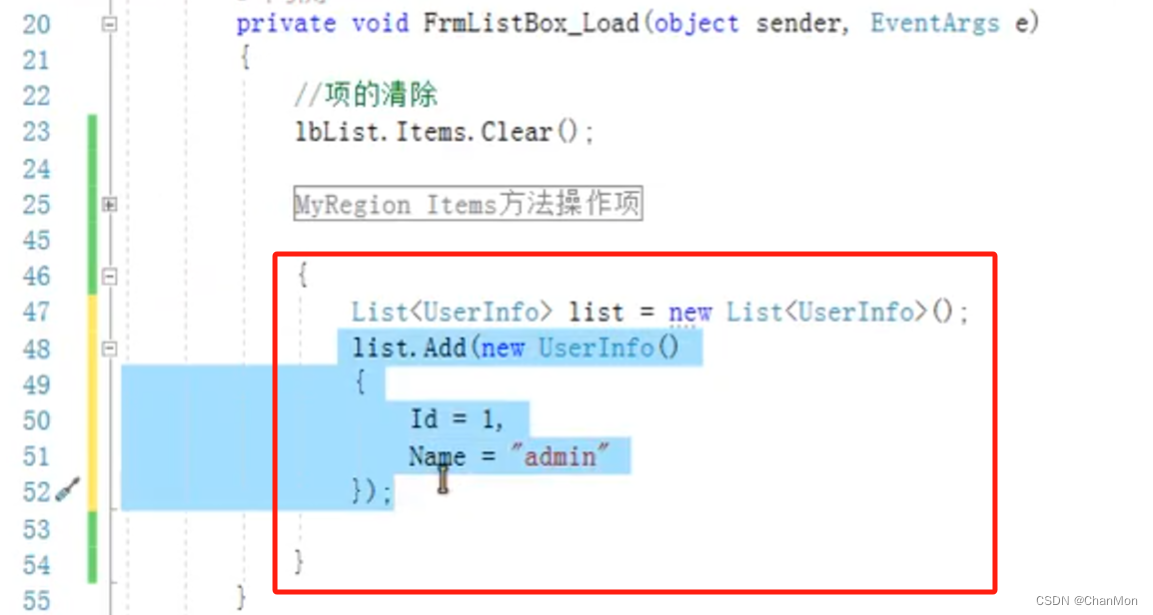
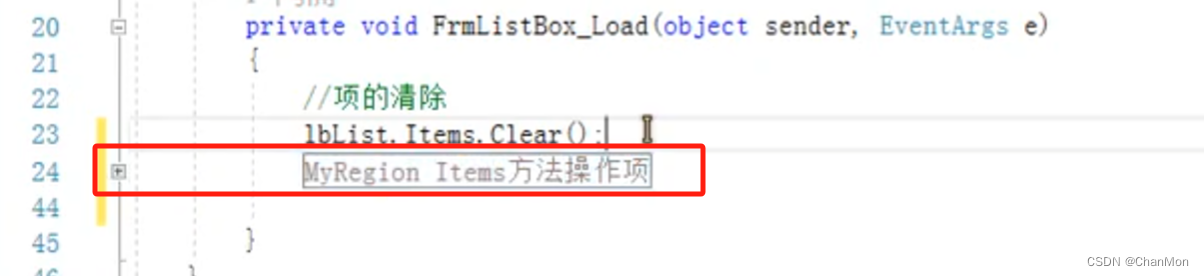
lbList.Items.Clear();
{List<UserInfo> list = new List<UserInfo>();list.Add(new UserInfo()){Id = 1,Name = "admin"});list.Add(new UserInfo()){Id = 2,Name = "lycchun"});list.Add(new UserInfo()){Id = 3,Name = "lwb"});list.Add(new UserInfo()){Id = 4,Name = "Eleven"});list.Add(new UserInfo()){Id = 5,Name = "Jason"});
}
4. 将构建的数据源添加到 ListBox
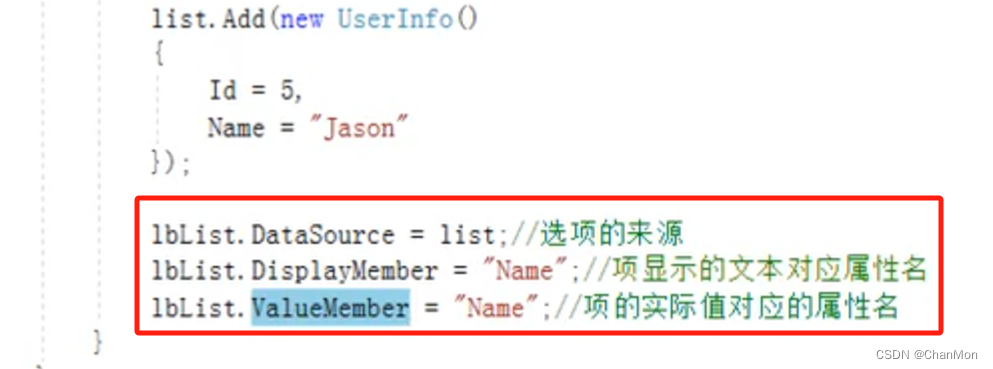
注意:当用Items添加项的时候,如果添加的每个项也是这种对象的话,也要加上这两句话:
lbList.DisplayMember = "Name"; //项显示的文本对应属性名
lbList.ValueMember = "Name"; //项的实际值对应的属性名
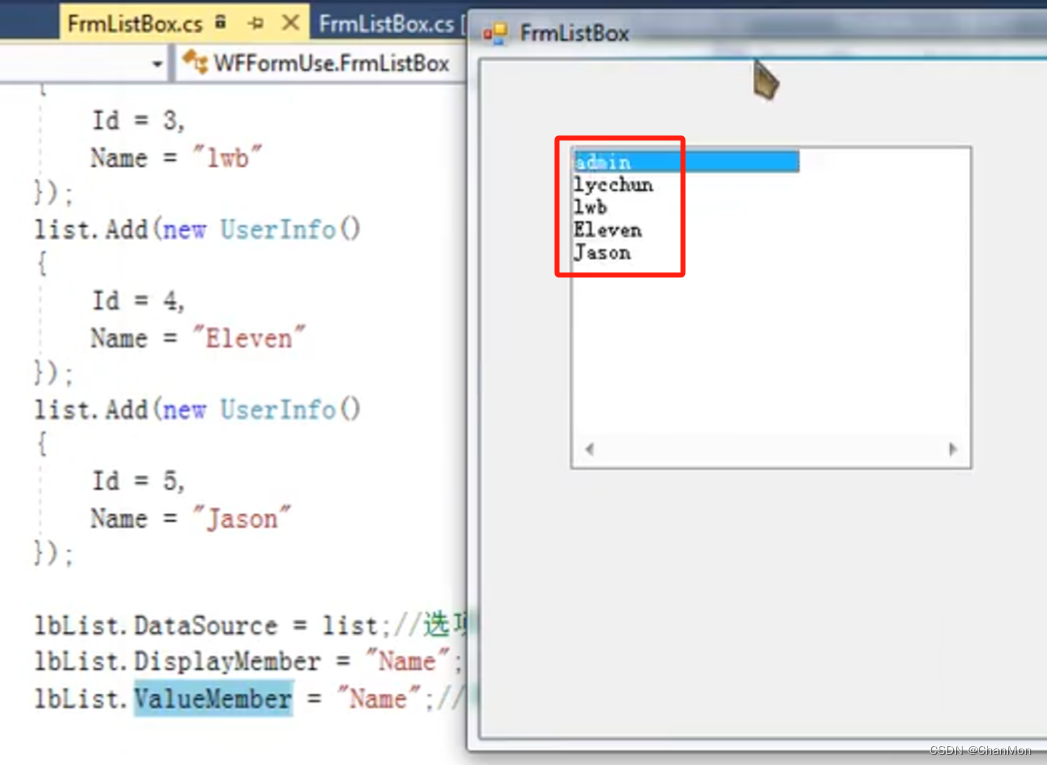
5. 对显示的文本进行操作
在窗体界面添加一个按钮,通过 点击按钮 执行操作
5.1 显示选中项的内容

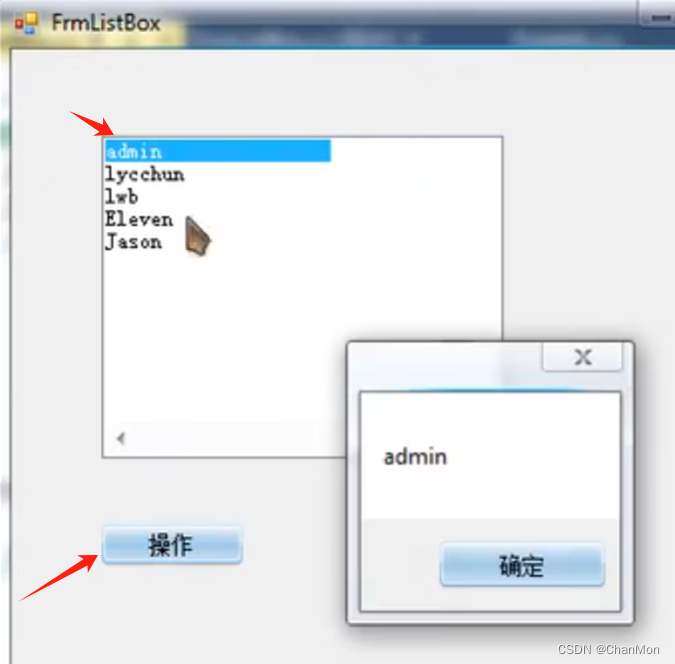
将实际值对应的属性名改为 ID(一般来说,项的实际值,会指定对应显示值的编号),再重新运行

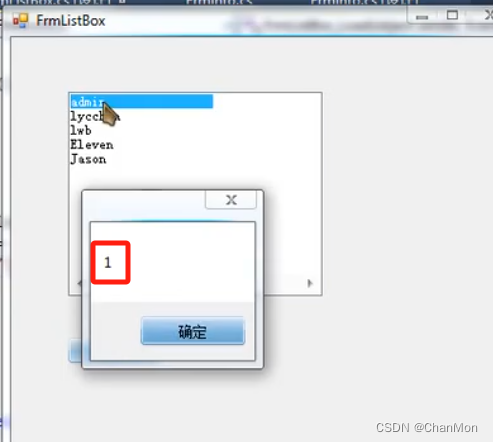
5.2 在 TextBox 中显示选中的多项的索引、ID、Name
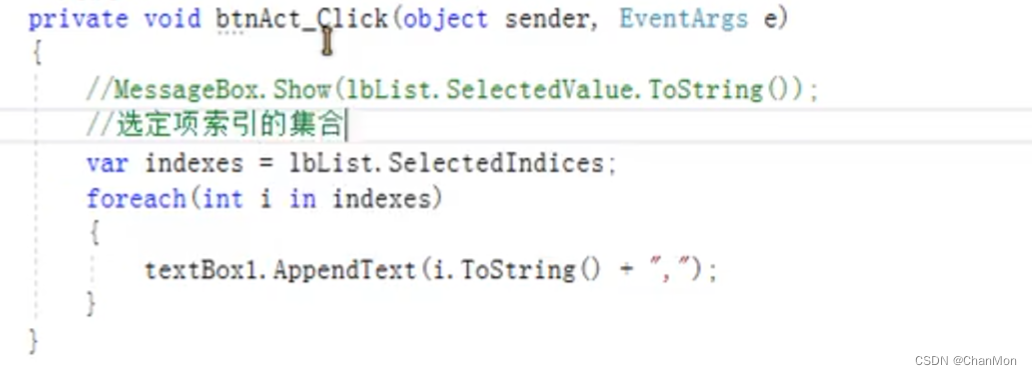
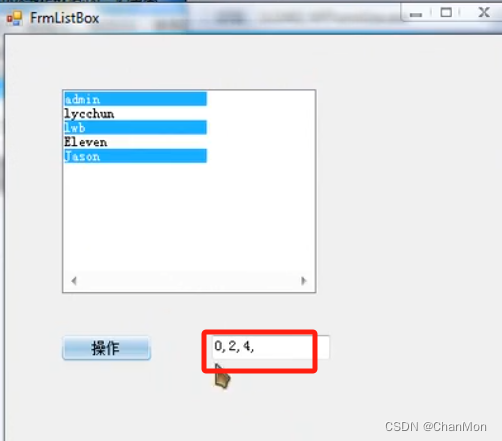
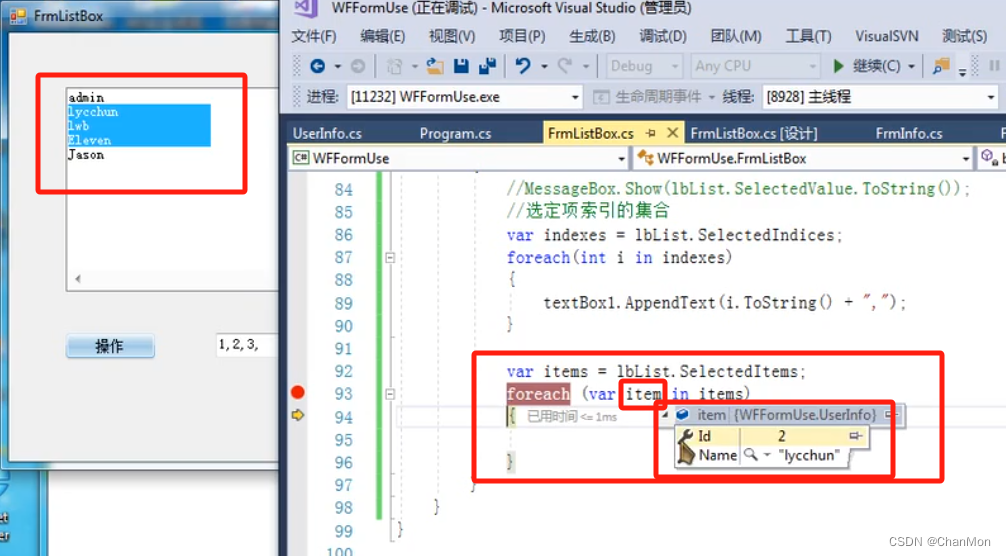
遍历选定项的 ID、Name
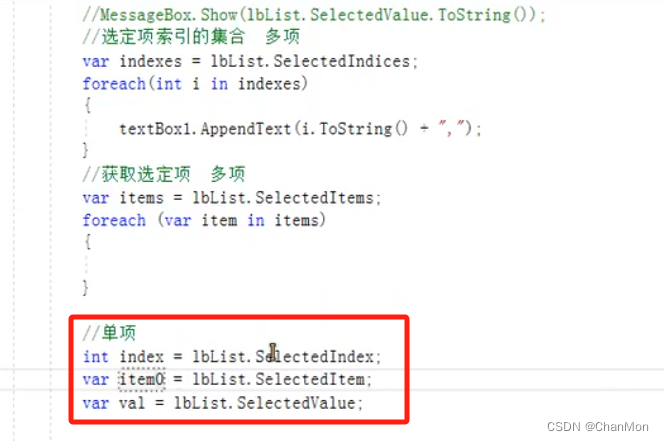
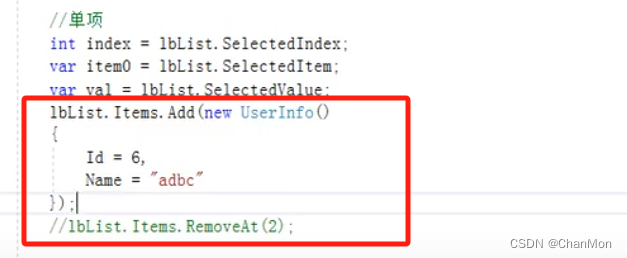
5.3 单项的操作
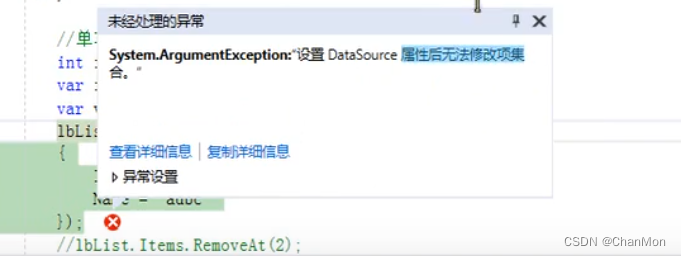
5.4 设置DataSource之后,无法修改项的集合
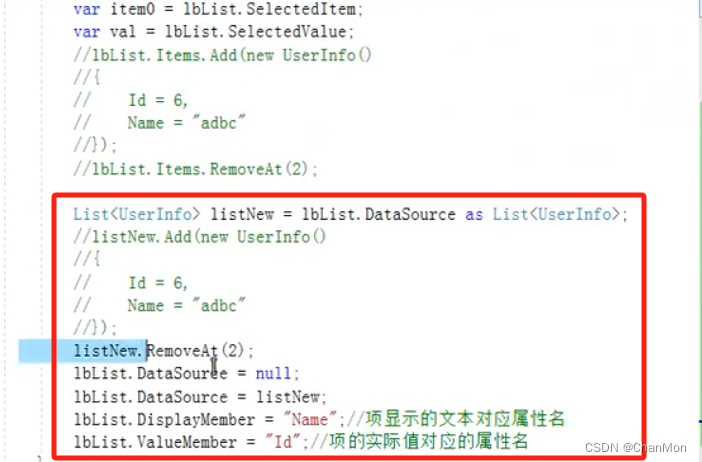
解决方法:把对 对象的操作 变成 对数据源的操作
region折叠代码
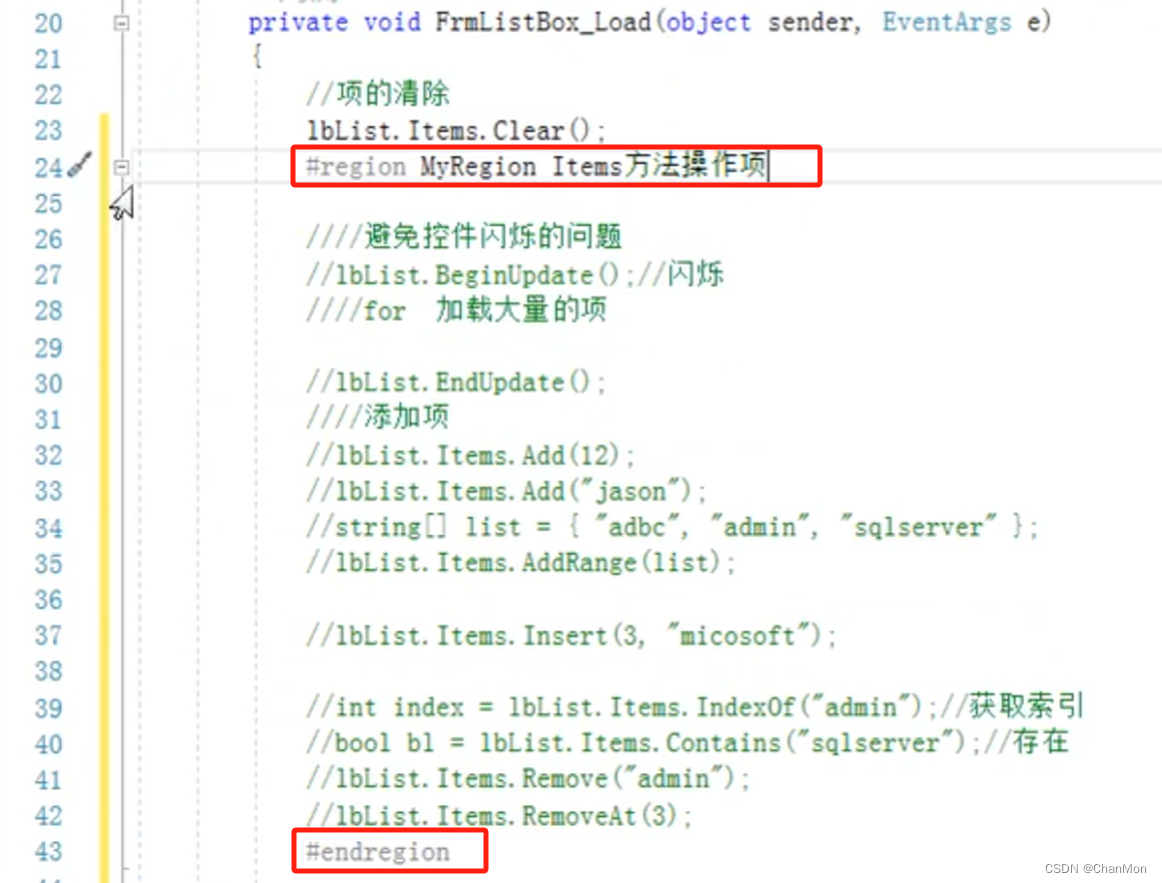
折叠后:
参考:2023年C#之WinForm零基础教程50讲
相关文章:

C# WinForm —— 12 ListBox绑定数据
ListBox加载大量数据时,避免窗体闪烁的方法: 在加载语句的前后分别加上 BeginUpdate()方法 和 EndUpdate()方法 指定一个集合为绑定的数据源 1. 首先,右键项目,添加类 2. 在新建的类文件中添加属性值信息 3. 构建初始化的对象…...

自动驾驶主流芯片及平台架构(二)特斯拉自动驾驶芯片平台介绍
早期 对外采购mobileye EyeQ3 芯片摄像头半集成方案,主要是为了满足快速量产需求,且受制于研发资金不足限制; 中期 采用高算力NVIDIA 芯片平台其他摄像头供应商的特斯拉内部集成方案,mobileye开发节奏无法紧跟特斯拉需求ÿ…...

powershell@管道符过滤的顺序问题@powershell管道符如何工作
文章目录 select 和 where谁先执行powershell管道符stop-service 为例查看文档中的典型参数介绍stop-process为例介绍管道符传参是怎么工作的Id参数InputObject 参数Name参数额外的试验反面例子应用:get-process 和stop-process配合 select 和 where谁先执行 在执行筛选时&…...

SMI接口
目录 SMI 接口帧格式读时序写时序 IP 设计IP 例化界面IP 接口IP 验证 SMI 接口 SMI(Serial Management Interface)串行管理接口,也被称作 MII 管理接口(MII Management Interface),包括 MDC 和 MDIO 两条信…...

【C++】转换构造函数和类型转换函数
目录 转换构造函数转换构造函数调用 类型转换函数类型转换函数定义形式应用 转换构造函数 转换构造函数就是一种构造函数,将一个其他类型的数据转换成一个类的对象的构造函数。 类型->类对象 转换构造函数调用 (1)显式强制类型转换&…...
全栈开发之路——前端篇(5)组件间通讯和接口等知识补充
全栈开发一条龙——前端篇 第一篇:框架确定、ide设置与项目创建 第二篇:介绍项目文件意义、组件结构与导入以及setup的引入。 第三篇:setup语法,设置响应式数据。 第四篇:数据绑定、计算属性和watch监视 辅助文档&…...
4.【Orangepi Zero2】Linux定时器(signal、setitimer),软件PWM驱动舵机(SG90)
Linux定时器(signal、setitimer),软件PWM驱动舵机(SG90) signalsetitimer示例 软件PWM驱动舵机(SG90) signal 详情请看Linux 3.进程间通信(shmget shmat shmdt shmctl 共享内存、si…...
K8S哲学 - 资源调度 HPA (horizontal pod autoScaler-sync-period)
kubectl exec: kubectl exec -it pod-name -c container-name -- /bin/sh kubectl run 通过一个 deployment来 演示 apiVersion: apps/v1 kind: Deployment metadata:name: deploylabels: app: deploy spec: replicas: 1selector: matchLabels:app: deploy-podt…...
uniapp/微信小程序实现加入购物车点击添加飞到购物车动画
1、预期效果 2、实现思路 每次点击添加按钮时,往该按钮上方添加一个悬浮元素,通过位移动画将元素移到目标位置。 1. 为每个点击元素设置不同的class,才能通过uni.createSelectorQuery来获取每个元素的节点信息; 2. 添加一个与…...

电商大数据的采集||电商大数据关键技术【基于Python】
.电商大数据采集API 什么是大数据? 1.大数据的概念 大数据即字面意思,大量数据。那么这个数据量大到多少才算大数据喃?通常,当数据量达到TB乃至PB级别时,传统的关系型数据库在处理能力、存储效率或查询性能上可能会遇…...

H264 SP帧等知识笔记
H.264是一种广泛使用的视频编码标准,它使用多种类型的帧来实现高效的视频压缩。在H.264中,参考帧和重建帧是两个重要的概念,它们之间既有区别又有联系。 参考帧: 参考帧是用于预测其他帧的帧。在H.264中,编码器会利用…...

流量印钞机:每日稳定收入1500+
标题:“流量印钞机:每日稳定收入1500” 随着互联网的迅速发展,越来越多的人开始利用网络平台来赚取稳定的收入。在这个信息爆炸的时代,拥有了一定的流量就意味着拥有了一台“印钞机”,可以每日稳定地创造超过1500元的…...

Tomcat中服务启动失败,如何查看启动失败日志?
1. 查看 localhost.log 这个日志文件通常包含有关特定 web 应用的详细错误信息。运行以下命令查看 localhost.log 中的错误: sudo tail -n 100 /opt/tomcat/latest/logs/localhost.YYYY-MM-DD.log请替换 YYYY-MM-DD 为当前日期,或选择最近的日志文件日…...
React19学习-初体验
升级react19版本 安装 npm install reactbeta react-dombeta如果使用ts则需要在package.json中添加。等正式版发布直接可以使用types/react了 "overrides": {"types/react": "npm:types-reactbeta","types/react-dom": "npm:ty…...

【UE5】数字人基础
这里主要记录一下自己在实现数字人得过程中涉及导XSens惯性动捕,视频动捕,LiveLinkFace表捕,GRoom物理头发等。 一、导入骨骼网格体 骨骼网格体即模型要在模型雕刻阶段就要雕刻好表捕所需的表情体(blendshape),后面表捕的效果直…...

OSTEP Projects:KV
本文将介绍操作系统导论(Operating Systems: Three Easy Pieces)作者所开源的操作系统相关课程项目 的 KV 部分,包含个人的代码实现和设计思路。 思路 题目要求实现一个最简单的数据库,以支持数据的持久化。 每个操作由格式为 o…...
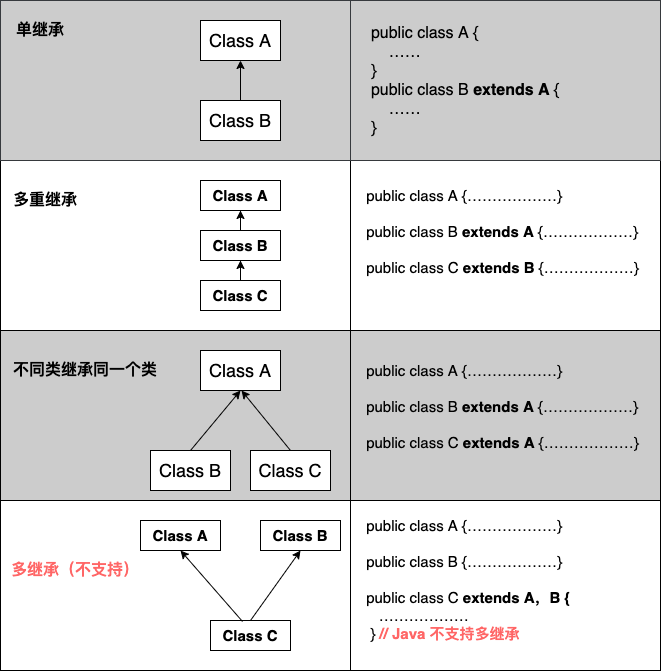
JAVA学习笔记(第三周)
文章目录 继承概述使用场景继承的特点子类继承的内容成员变量访问特点成员方法访问特点方法的重写构造方法this super 多态多态的表现形式多态的前提成员变量和方法调用instanceof优势弊端 包包名的规则全类名final常量 权限修饰符代码块 继承 概述 继承就是子类继承父类的特征…...

linux 内核驱动 -- reboot -f 导致内核死机 而 reboot则不会引起问题
问题描述,定于与解决:...
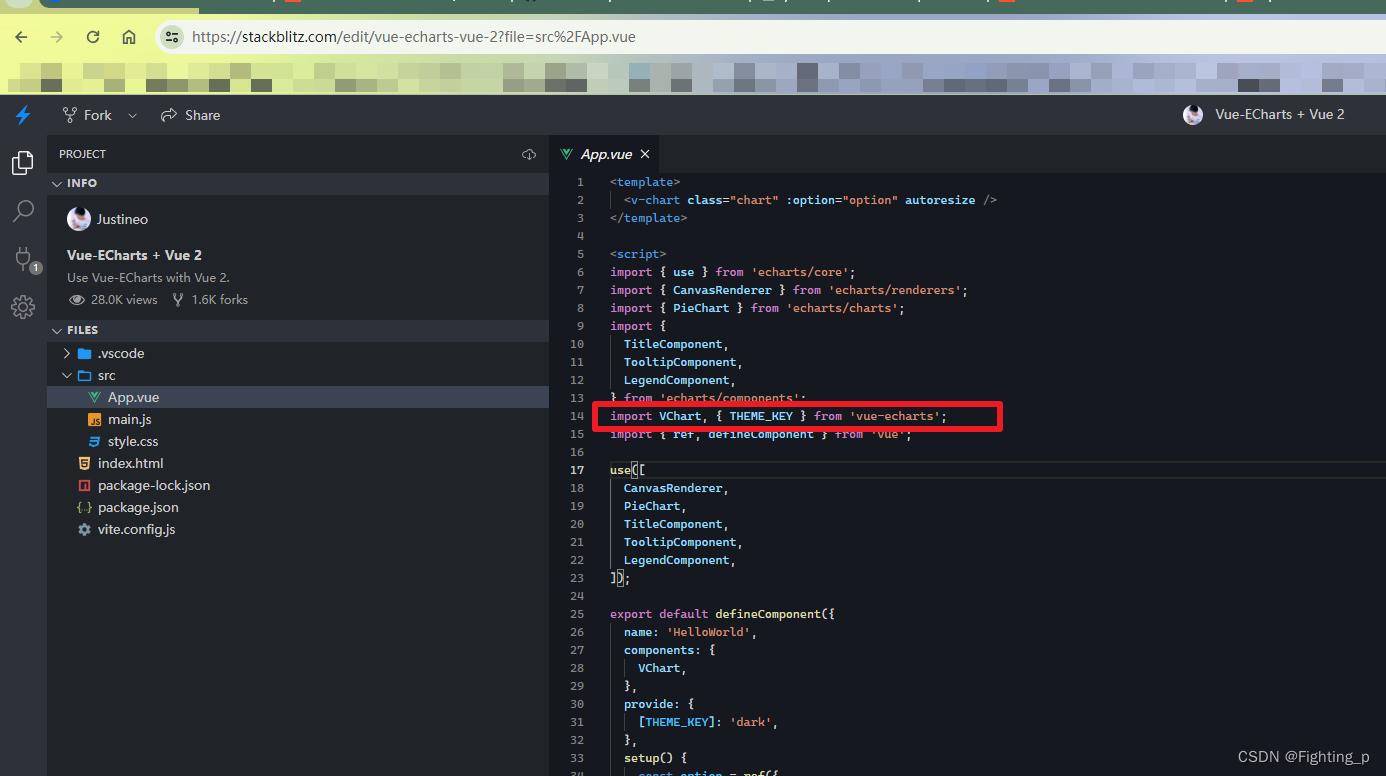
【vue-echarts】 报错问题解决 “Error: Component series.pie not exists. Load it first.“
目录 问题描述解决【解决1】【解决2】 问题描述 使用 vue-echarts 时导入的文件 import VChart from vue-echarts/components/ECharts import echarts/lib/chart/line import echarts/lib/chart/bar import echarts/lib/chart/pie import echarts/lib/component/legend impor…...

MySQL慢查询SQL优化
一、慢查询日志 描述:通过慢查询日志等定位那些执行效率较低的SQL语句 查看 # 慢查询是否开启 show variables like slow_query_log%; # 慢查询超时时间 show variables like long_query_time%;执行SQL 开启慢查询日志 set global slow_query_log ON;设置慢查…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
