每周一算法:无向图的最小环
题目链接
观光之旅
题目描述
给定一张无向图,求图中一个至少包含 3 3 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。
该问题称为无向图的最小环问题。
你需要输出最小环的方案,若最小环不唯一,输出任意一个均可。
输入格式
第一行包含两个整数 N N N 和 M M M,表示无向图有 N N N 个点, M M M 条边。
接下来 M M M 行,每行包含三个整数 u , v , l u,v,l u,v,l,表示点 u u u 和点 v v v 之间有一条边,边长为 l l l。
输出格式
输出占一行,包含最小环的所有节点(按顺序输出),如果不存在则输出 No solution.。
样例 #1
样例输入 #1
5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20
样例输出 #1
1 3 5 2
提示
【数据范围】
1 ≤ N ≤ 100 1≤N≤100 1≤N≤100,
1 ≤ M ≤ 10000 1≤M≤10000 1≤M≤10000,
1 ≤ l < 500 1≤l<500 1≤l<500
算法思想
根据题目描述,求的是无向图中的最小环,要求环中至少包含 3 3 3 个节点,且环上的节点不重复。当边权都为正数式,最小环中的节点一定不会重复,否则就不是最小环了,如下图所示。
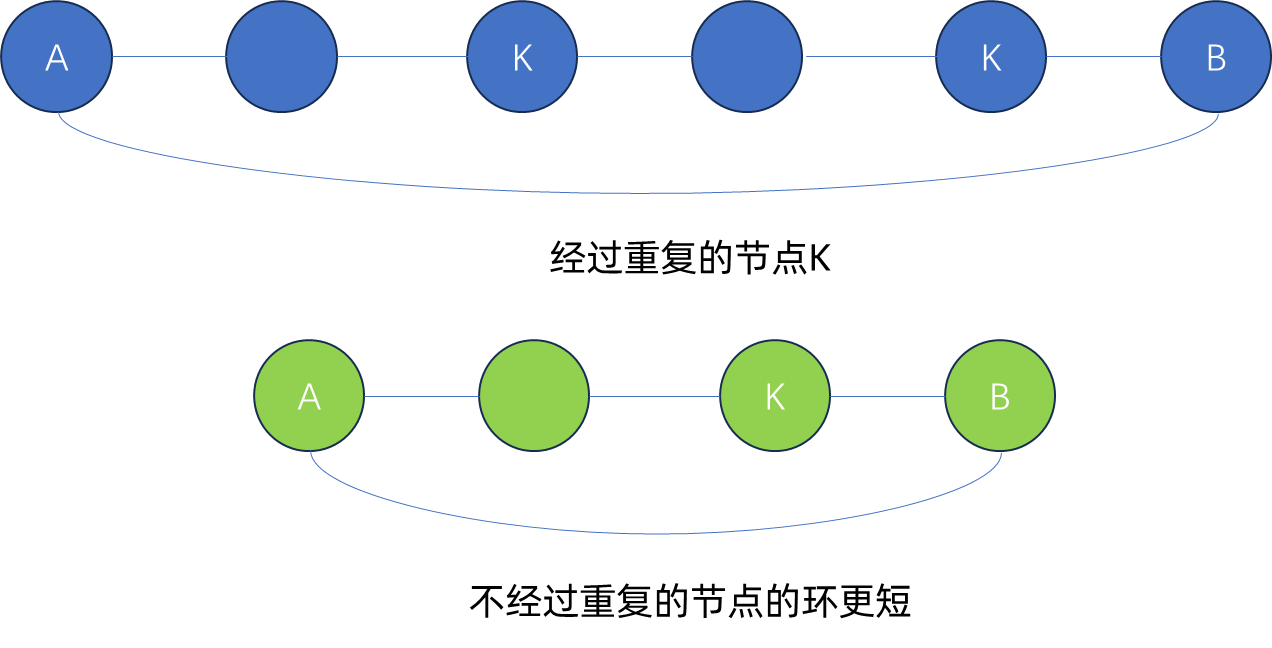
求最小环的长度
无向图的最小环问题可以使用「Floyd」算法解决。基本思想是:
- 当外层循环 k k k刚开始时, d [ i , j ] d[i,j] d[i,j]保存着从节点 i i i到 j j j经过编号不超过 k − 1 k-1 k−1的最短路径长度
- 此时,如果引入新节点 k k k构成了环,那么环的长度为 d [ i , j ] + g [ j ] [ k ] + g [ k ] [ i ] d[i,j]+g[j][k]+g[k][i] d[i,j]+g[j][k]+g[k][i],如下图所示:
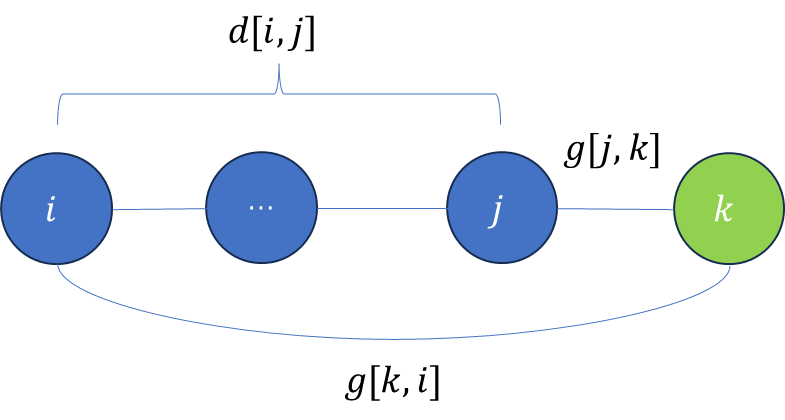
那么, m i n { d [ i , j ] + g [ j ] [ k ] + g [ k ] [ i ] } min\{d[i,j]+g[j][k]+g[k][i]\} min{d[i,j]+g[j][k]+g[k][i]},其中 1 ≤ i < j < k 1\le i\lt j\lt k 1≤i<j<k,就是满足以下两个条件的最小环长度:- 由编号不超过 k k k的节点构成
- 经过节点 k k k
从 1 ∼ n 1\sim n 1∼n枚举 k k k,取上式的最小值,就可以得到整张图的最小环长度。
求最小环上的节点
除了计算最小环之外,题目还要求记录最小环的上所有节点。当更新最小环时,环上的节点包含 i i i、 i i i到 j j j之间最短路上的节点,以及 i i i和 k k k。那么如何得到 i i i到 j j j之间最短路上的节点
使用Floyd算法计算最短路时,当 d [ i ] [ j ] > d [ i ] [ k ] + d [ k ] [ j ] d[i][j]>d[i][k]+d[k][j] d[i][j]>d[i][k]+d[k][j]时,可以更新节点 i i i到 j j j的最短路,同时记录节点 i i i到 j j j的最短路是经过 k k k点中转得到的,不妨记 p o s [ i , j ] = k pos[i,j]=k pos[i,j]=k。
那么经过节点 i i i到 j j j的最短路径的可以分成两个部分:
- 节点 i i i到 k k k的最短路
- 节点 k k k到 j j j的最短路
可以通过递归的方式,分别获取这两部分经过的节点。
时间复杂度
Floyd算法内可以同时求最小环和最短路,因此时间复杂度为 O ( n 3 ) O(n^3) O(n3)。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 105, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], d[N][N];
int pos[N][N];//pos[i][j]表示i和j最短路经过k点中转
vector<int> path; //保存最小环路径
void get_path(int i, int j)
{if(pos[i][j] == 0) return; //i和j之间不存在中转点int k = pos[i][j]; //k是i和j最最短路的中转点get_path(i, k); //递归后取i-k最短路上的节点path.push_back(k);get_path(k, j); //递归后取k-j最短路上的节点
}
int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g); //初始化邻接矩阵for(int i = 1; i <= n; i ++) g[i][i] = 0;while (m -- ){int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = min(g[a][b], c); //无向图,可能存在重边}int ans = INF;memcpy(d, g, sizeof d); //初始化最短路for(int k = 1; k <= n; k ++){//计算由编号不超过k的节点构成的最小环for(int i = 1; i < k; i ++) //枚举环中的点for(int j = i + 1; j < k; j ++){if((long long)d[i][j] + g[j][k] + g[k][i] < ans) //出现更小的环{ans = d[i][j] + g[j][k] + g[k][i];path.clear(); //清除之前的最小环路径path.push_back(k); //k-i-最短路路径-jpath.push_back(i);get_path(i, j);//获取i-j最短路径上的节点path.push_back(j);}}//计算最短路for(int i = 1; i <= n; i ++)for(int j = 1; j <= n; j ++)if(d[i][j] > d[i][k] + d[k][j]){d[i][j] = d[i][k] + d[k][j];pos[i][j] =k; //记录最短路中转点}}if(ans == INF) puts("No solution.");else //存在最小环{for(int i : path) cout << i << " ";}
}
相关文章:

每周一算法:无向图的最小环
题目链接 观光之旅 题目描述 给定一张无向图,求图中一个至少包含 3 3 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。 该问题称为无向图的最小环问题。 你需要输出最小环的方案,若最小环不唯一,输出…...
分布式websocket IM即时通讯聊天开源项目如何启动
前言 自己之前分享了分布式websocket的视频有同学去fork项目了,自己启动一下更方便理解项目嘛。然后把项目启动需要的东西全部梳理出来。支持群聊单聊,表情包以及发送图片。 支持消息可靠,消息防重,消息有序。同时基础架构有分布式权限&…...
环境准备写个简单例子(小白手册)-20240506)
tensorflow学习笔记(1)环境准备写个简单例子(小白手册)-20240506
一、安装python、tensorflow 1、Mac上默认python已经安装,自带pip 2、pip3 install tensorflow 如果报错,提示pip3版本较低,可以根据提示来更新pip3:/Library/Developer/CommandLineTools/usr/bin/python3 -m pip install --upgrade pip 3、然后再使用pip3来安装tensor…...
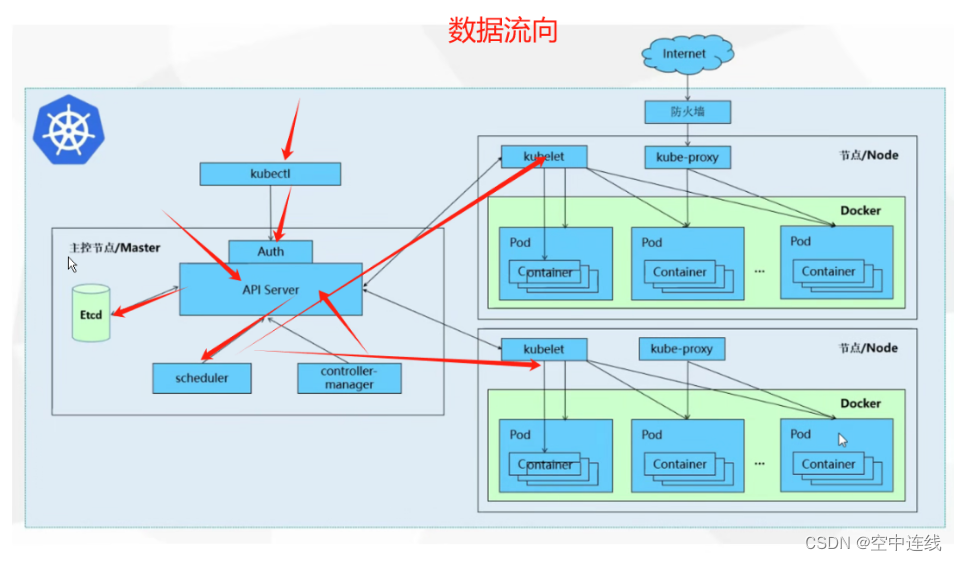
kubernate 基本概念
一 K8S 是什么? K8S 全称:Kubernetes 1 kubernate基本概念 作用: 用于自动部署、扩展和管理“容器化(containerized)应用程序”的开源系统。 可以理解成 K8S 是负责自动化运维管理多个容器化程序(比如…...
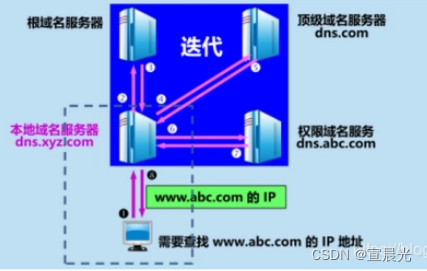
【系统架构师】-选择题(十二)计算机网络
1、网闸的作用:实现内网与互联网通信,但内网与互联网不是直连的 2、管理距离是指一种路由协议的路由可信度。15表示该路由信息比较可靠 管理距离越小,它的优先级就越高,也就是可信度越高。 0是最可信赖的,而255则意味…...

代码随想录|总结篇
完结篇: 60天,还是坚持了下来,达成算法路上的一个小目标。 加入代码随想录训练营之前,也断断续续刷到了树那一章节,但后面因为导师项目等种种情况,一直耽搁到年后。年后打算重新开始刷题时,正好…...

网络编程套接字和传输层tcp,udp协议
认识端口号 我们知道在网络数据传输的时候,在IP数据包头部有两个IP地址,分别叫做源IP地址和目的IP地址。IP地址是帮助我们在网络中确定最终发送的主机,但是实际上数据应该发送到主机上指定的进程上的,所以我们不仅要确定主机&…...

通过wget下载ftp文件
通过wget下载ftp文件 基础用法带密码的http文件带密码的ftp文件补充 基础用法 在下载的过程中会显示进度条,包含百分比,已下载字节,下载速度,剩余时间。 # 下载单个文件 wget [url_file]# 下载目录全部文件 wget [url_dir/*] wg…...

Acrobat Pro DC 2023 for Mac:PDF处理的终极解决方案
Acrobat Pro DC 2023 for Mac为Mac用户提供了PDF处理的终极解决方案。它具备强大的文档处理能力,无论是查看、编辑还是创建PDF文件,都能轻松胜任。在编辑功能方面,Acrobat Pro DC 2023支持对文本、图像进行精准的修改和调整,还能添…...

map容器
目录 map构造和赋值 map大小和交换 map插入和删除 map查找和统计 map排序 map构造和赋值 map中所有元素都是pair(即一对) pair中第一个元素为key(键值),起到索引作用,第二个元素为value(…...

GNU/Linux - 是否可以多次打开同一个设备文件
使用设备/dev/ttyS1举例来说明。 一个设备文件打开多次 在 Linux 中,多次打开 /dev/ttyS1 以读取数据通常是可以接受的。多次打开 /dev/ttyS1 并向 /dev/ttyS1 发送数据时,所有打开的文件描述符都能接收数据。每个打开的文件描述符都代表与串行端口的独立…...
Visual Studio的使用方法
目录 1. 下载软件 2. 软件安装 3. 软件使用 4. VS工具的字体背景美化 5. 程序调试 1. 下载软件 官网地址:Visual Studio 2022 IDE - 适用于软件开发人员的编程工具 (microsoft.com) 2. 软件安装 1.选中vs_Professional,鼠标右击选择“以管理员身份…...

【35分钟掌握金融风控策略18】贷前风控策略详解-3
目录 编辑 贷前风控数据源 第三方数据 贷前风控数据源 第三方数据 在金融风控过程中,金融机构通常会引入一些第三方的风控数据(或第三方金融技术)来辅助识别贷款个人或贷款企业的风险状况,帮助金融机构进行风控决策&#x…...

秋招后端开发面试题 - MySQL事务
目录 MySQL事务前言面试题什么是数据库事务为什么要有事务呢?项目中遇到的事务事务的传播机制事务的特性?事务并发存在的问题四大隔离级别四大隔离级别,都会存在哪些并发问题呢数据库是如何保证事务的隔离性的呢?如何解决加锁后的…...

C语言栈的含义与栈数据操作代码详解!
引言:在本篇博客中,我们将学到数据结构——栈,讲到栈的含义与关于栈的数据操作代码。栈可以在顺序表、双向链表以及单链表的基础上实现,而于本篇博客中,我们选择在顺序表的基础上实现栈。 更多有关C语言和数据结构知识…...
数据库基础语法二
一、数据库 1、登陆数据库 2、创建数据库zoo 3、修改数据库zoo字符集为gbk 4、选择当前数据库为zoo 5、查看创建数据库zoo信息 6、删除数据库zoo mysql -uroot -p #登陆数据库 create database zoo; #创建数据库zoo alter database zoo character set gbk collate gbk_…...

数据库的一些知识点
在Sno between列上创建约束,要求Sno的值在18至22岁之间,约束名Sno_CK。请写出对应的完整性命名子句constraint Sno_CK primary key check and。 本题得分: 0分 正确答案: 填空1 : 学号填空2 : snobetween18and22 2.单选题 (12分) 下述SQL命令的短语中…...
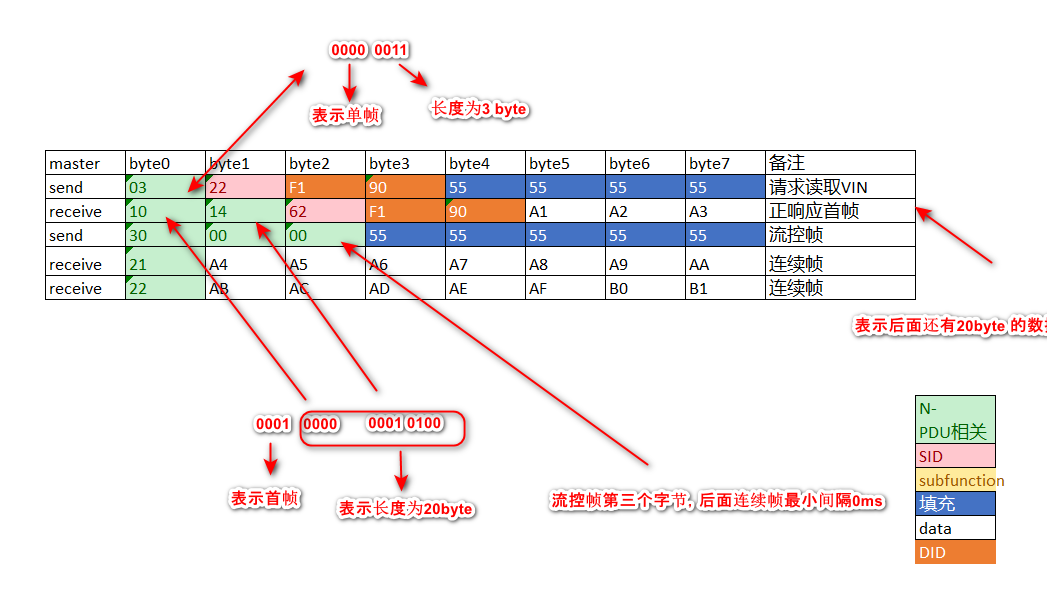
[AutoSar]BSW_Com021单帧 首帧 流控帧 连续帧 详解
目录 关键词平台说明一、N_PDU和N_PCI二、单帧三、首帧四、流控帧五、连续帧六、case 关键词 嵌入式、C语言、autosar、OS、BSW、UDS、diagnostic 平台说明 项目ValueOSautosar OSautosar厂商vector , EB芯片厂商TI 英飞凌编程语言C,C编译器HighTec (…...

CSS学习笔记之中级教程(一)
1、CSS 布局 - display 属性 1.1 display 属性 display 属性是用于控制布局的最重要的 CSS 属性。 display 属性规定是否/如何显示元素。 每个 HTML 元素都有一个默认的 display 值,具体取决于它的元素类型。大多数元素的默认 display 值为 block 或 inline。 …...
Spring Cloud Alibaba 网关 Gateway 集成(7)
项目的源码地址 Spring Cloud Alibaba 工程搭建(1) Spring Cloud Alibaba 工程搭建连接数据库(2) Spring Cloud Alibaba 集成 nacos 以及整合 Ribbon 与 Feign 实现负载调用(3) Spring Cloud Alibaba Ribbo…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
