【外币兑换,简单贪心】
小明刚从美国回来,发现手上还有一些未用完的美金,于是想去银行兑换成人民币。可是听说最近人民币将会升值,并从金融机构得到了接下来十二个月可能的美元对人民币汇率,现在,小明想要在接下来一年中把美金都兑换成人民币,请问最多能得到多少人民币?
输入
输入的第一行是一个实数N(1.00<=N<=100.00),表示小明现有的美金数量。
接下来一行,包含12个实数ai,表示接下来十二个月的美元对人民币汇率。
输出
输出一个小数R,表示小明最多能获得的人民币数量,结果保留两位小数。
样例输入 复制
46.91
6.31 6.32 6.61 6.65 5.55 5.63 6.82 6.42 6.40 5.62 6.78 5.60样例输出 复制
319.93思路:
1.读完题有点疑惑是全部在兑换率最大的一个月换,还是该给每个月分配多少钱兑换
2.直接猜想将全部美元都在兑换率最大的一个月换---->>>带入数据验证
#include <bits/stdc++.h>
using namespace std;
int main()
{double n;double a[12];cin>>n;for(int i=0;i<12;i++){cin>>a[i];}sort(a,a+12);double t=a[11]*n; //最大兑换率乘总金额printf("%.2f",t);return 0;}相关文章:

【外币兑换,简单贪心】
小明刚从美国回来,发现手上还有一些未用完的美金,于是想去银行兑换成人民币。可是听说最近人民币将会升值,并从金融机构得到了接下来十二个月可能的美元对人民币汇率,现在,小明想要在接下来一年中把美金都兑换成人民币…...
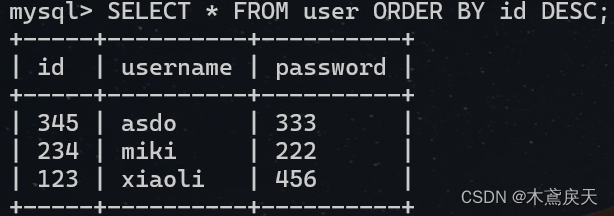
数据库入门(sql文档+命令行)
一.基础知识 1.SQL(Structured Query Language)结构化查询语言分类: DDL数据定义语言用来定义数据库对象:数据库、表、字段DML数据操作语言对数据库进行增删改查DQL数据查询语言查询数据库中表的信息DCL数据控制语言用来创建数据…...
【机器学习300问】84、AdaGrad算法是为了解决什么问题?
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题,解决这个问题的过程称为最优化。因为参数空间非常复杂,无法轻易找到最优解,而且在深度神经网络中,参数的数量非常庞大,导致最优化问…...

Java算法-力扣leetcode-14. 最长公共前缀
14. 最长公共前缀 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 ""。 示例 1: 输入: strs ["flower","flow","flight"] 输出: "fl"示…...
视频拼接融合产品的产品与架构设计(二)
视频拼接融合产品的产品与架构设计一 以上是第一期,以前思考的时候还是比较着急,现在思考的更多了,现实世界的拼接更加需要我们沉下心来做,尤其是对于更多画面,画面更加清晰怎么做 本篇章不在于其他功能,在…...

【docker 】push 镜像到私服
查看镜像 docker images把这个hello-world 推送到私服 docker push hello-world:latest 报错了。不能推送。需要标记镜像 标记Docker镜像 docker tag hello-world:latest 192.168.2.1:5000/hello-world:latest 将Docker镜像推送到私服 docker push 192.168.2.1:5000/hello…...
Java框架精品项目【用于个人学习】
源码获取:私聊回复【项目关键字】获取 更多选题参考: Java练手项目 & 个人学习等选题参考 推荐菜鸟教程Java学习、Javatpoint学习 前言 大家好,我是二哈喇子,此博文整理了各种项目需求 此文下的项目用于博主自己学习&#x…...
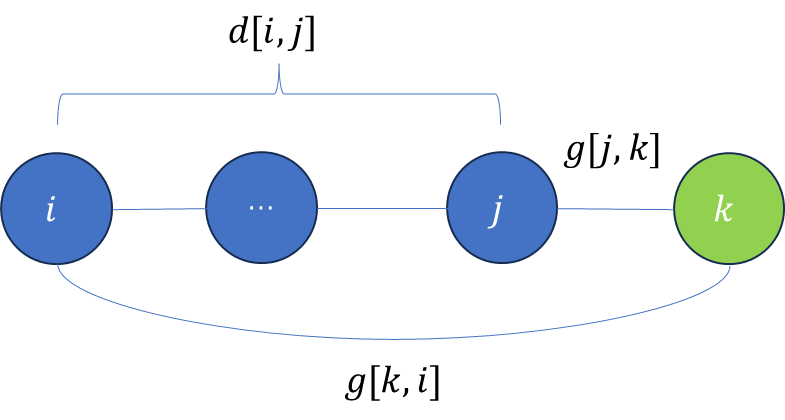
每周一算法:无向图的最小环
题目链接 观光之旅 题目描述 给定一张无向图,求图中一个至少包含 3 3 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。 该问题称为无向图的最小环问题。 你需要输出最小环的方案,若最小环不唯一,输出…...
分布式websocket IM即时通讯聊天开源项目如何启动
前言 自己之前分享了分布式websocket的视频有同学去fork项目了,自己启动一下更方便理解项目嘛。然后把项目启动需要的东西全部梳理出来。支持群聊单聊,表情包以及发送图片。 支持消息可靠,消息防重,消息有序。同时基础架构有分布式权限&…...
环境准备写个简单例子(小白手册)-20240506)
tensorflow学习笔记(1)环境准备写个简单例子(小白手册)-20240506
一、安装python、tensorflow 1、Mac上默认python已经安装,自带pip 2、pip3 install tensorflow 如果报错,提示pip3版本较低,可以根据提示来更新pip3:/Library/Developer/CommandLineTools/usr/bin/python3 -m pip install --upgrade pip 3、然后再使用pip3来安装tensor…...
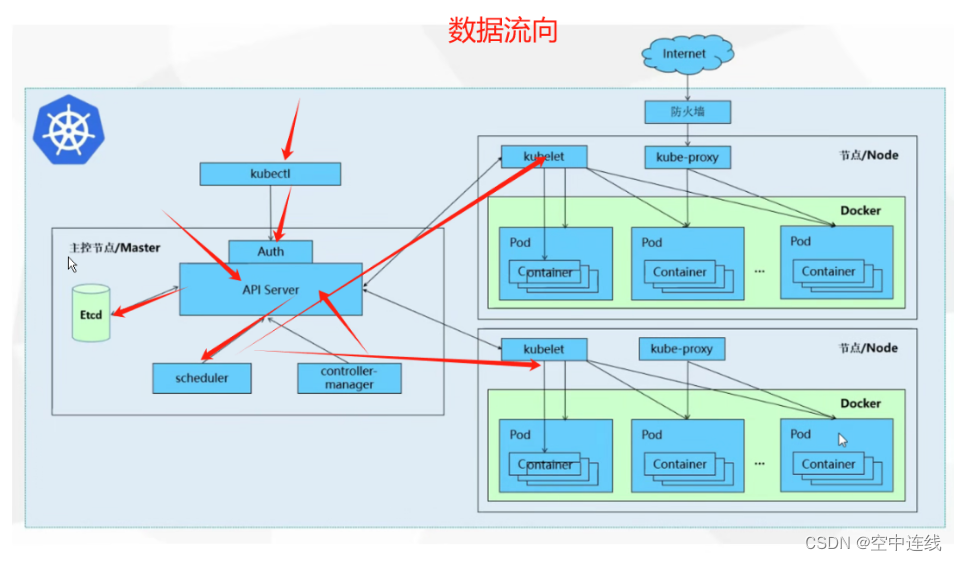
kubernate 基本概念
一 K8S 是什么? K8S 全称:Kubernetes 1 kubernate基本概念 作用: 用于自动部署、扩展和管理“容器化(containerized)应用程序”的开源系统。 可以理解成 K8S 是负责自动化运维管理多个容器化程序(比如…...
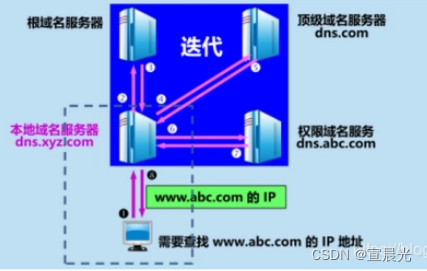
【系统架构师】-选择题(十二)计算机网络
1、网闸的作用:实现内网与互联网通信,但内网与互联网不是直连的 2、管理距离是指一种路由协议的路由可信度。15表示该路由信息比较可靠 管理距离越小,它的优先级就越高,也就是可信度越高。 0是最可信赖的,而255则意味…...

代码随想录|总结篇
完结篇: 60天,还是坚持了下来,达成算法路上的一个小目标。 加入代码随想录训练营之前,也断断续续刷到了树那一章节,但后面因为导师项目等种种情况,一直耽搁到年后。年后打算重新开始刷题时,正好…...

网络编程套接字和传输层tcp,udp协议
认识端口号 我们知道在网络数据传输的时候,在IP数据包头部有两个IP地址,分别叫做源IP地址和目的IP地址。IP地址是帮助我们在网络中确定最终发送的主机,但是实际上数据应该发送到主机上指定的进程上的,所以我们不仅要确定主机&…...

通过wget下载ftp文件
通过wget下载ftp文件 基础用法带密码的http文件带密码的ftp文件补充 基础用法 在下载的过程中会显示进度条,包含百分比,已下载字节,下载速度,剩余时间。 # 下载单个文件 wget [url_file]# 下载目录全部文件 wget [url_dir/*] wg…...

Acrobat Pro DC 2023 for Mac:PDF处理的终极解决方案
Acrobat Pro DC 2023 for Mac为Mac用户提供了PDF处理的终极解决方案。它具备强大的文档处理能力,无论是查看、编辑还是创建PDF文件,都能轻松胜任。在编辑功能方面,Acrobat Pro DC 2023支持对文本、图像进行精准的修改和调整,还能添…...

map容器
目录 map构造和赋值 map大小和交换 map插入和删除 map查找和统计 map排序 map构造和赋值 map中所有元素都是pair(即一对) pair中第一个元素为key(键值),起到索引作用,第二个元素为value(…...

GNU/Linux - 是否可以多次打开同一个设备文件
使用设备/dev/ttyS1举例来说明。 一个设备文件打开多次 在 Linux 中,多次打开 /dev/ttyS1 以读取数据通常是可以接受的。多次打开 /dev/ttyS1 并向 /dev/ttyS1 发送数据时,所有打开的文件描述符都能接收数据。每个打开的文件描述符都代表与串行端口的独立…...
Visual Studio的使用方法
目录 1. 下载软件 2. 软件安装 3. 软件使用 4. VS工具的字体背景美化 5. 程序调试 1. 下载软件 官网地址:Visual Studio 2022 IDE - 适用于软件开发人员的编程工具 (microsoft.com) 2. 软件安装 1.选中vs_Professional,鼠标右击选择“以管理员身份…...

【35分钟掌握金融风控策略18】贷前风控策略详解-3
目录 编辑 贷前风控数据源 第三方数据 贷前风控数据源 第三方数据 在金融风控过程中,金融机构通常会引入一些第三方的风控数据(或第三方金融技术)来辅助识别贷款个人或贷款企业的风险状况,帮助金融机构进行风控决策&#x…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
