AVL树的旋转
目录
1.平衡因子
2.旋转
a.节点定义
b.插入
插入
平衡因子更新
旋转
左单旋
右单旋
右左双旋
左右双旋
3.AVL树的验证
1.平衡因子
我们知道搜索二叉树有缺陷,就是不平衡,比如下面的树
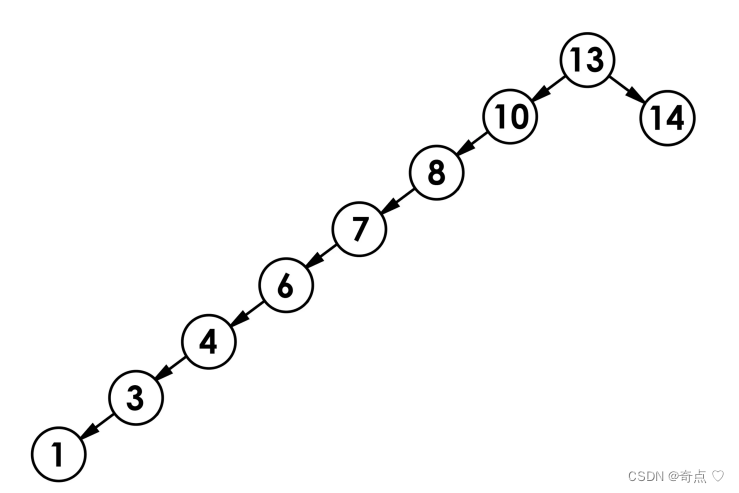
什么是搜索树的平衡?就是每个节点的左右子树的高度差不超过1,称平衡的搜索树为AVL树, 那我们怎么控制搜索树的平衡呢?
给出了平衡因子,每个节点的平衡因子=节点右子树的高度-节点左子树的高度(或者反过来,我们用前面那种)平衡因子=[-1,1],当超出这个范围,搜索树就不平衡了
树的平衡因子可以这样表示:

2.旋转
a.节点定义
template<class K,class V>
class AVLNode
{
public:typedef AVLNode<K,V> Node;AVLNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}Node* _left;Node* _right;Node* _parent;pair<K, V> _kv;//库里面提供的结构体,表示key和valueint _bf;//平衡因子};
b.插入
插入
左边小插左边,右边大插右边
template<class K,class V>
class AVLTree
{
public:typedef AVLNode<K, V> Node;bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv .first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//更新平衡因子//...............return true;}protected:
//........
private:Node* _root=nullptr;
};平衡因子更新
前面都好理解插入一个节点,那插入节点后平衡因子怎么更新呢?
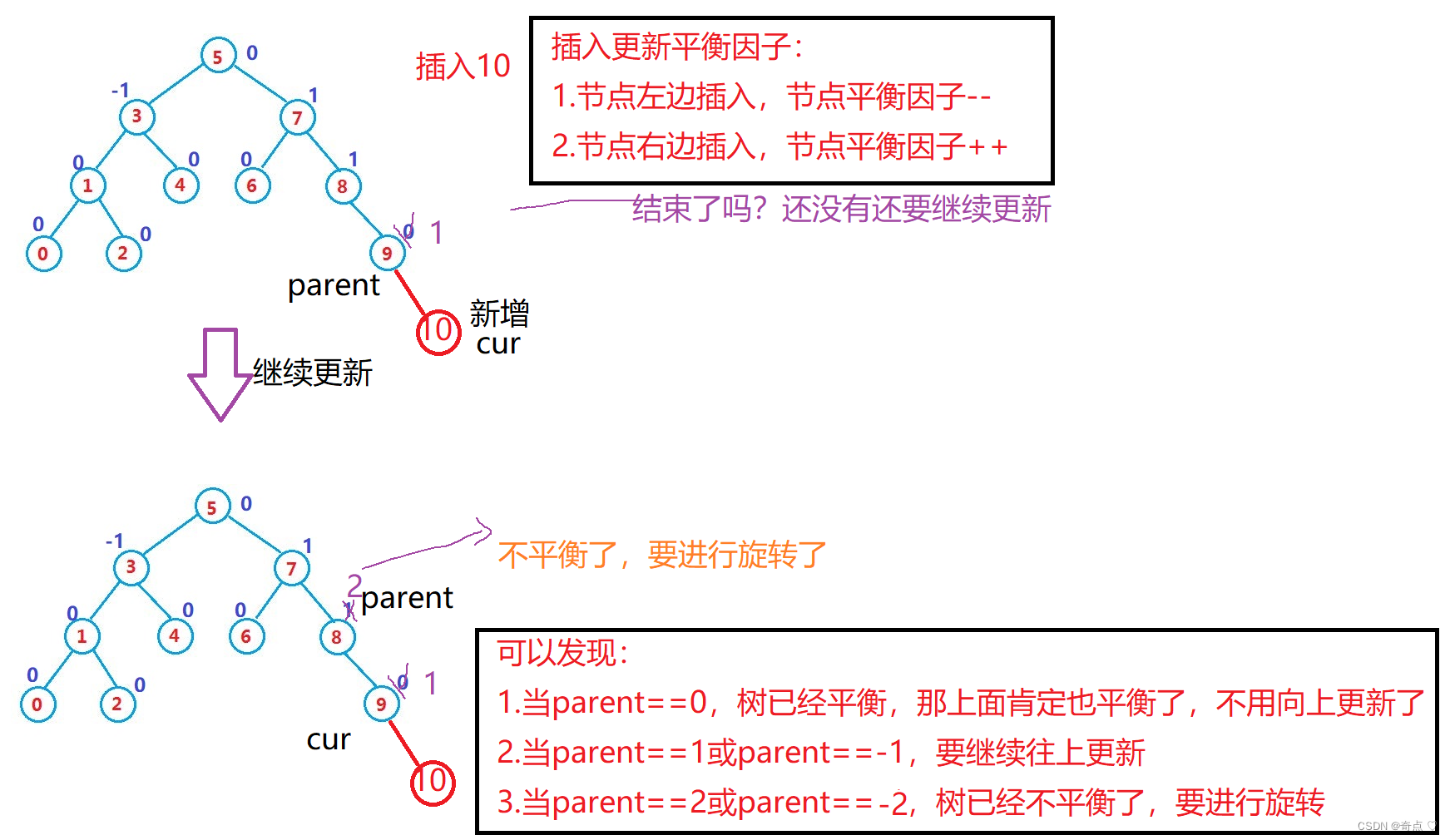
//更新平衡因子while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 1 || parent->_bf == -1){//继续更新parent = parent->_parent;cur =cur->_parent;}else if (parent->_bf == 0){//已经平衡break;}else if (parent->_bf == 2 || parent->_bf == -2){//进行旋转//...........}else{assert(false);//有可能不会出现上面的情况,出现大问题了,立马断死}break;//直接跳出了}旋转
有四种情况需要旋转
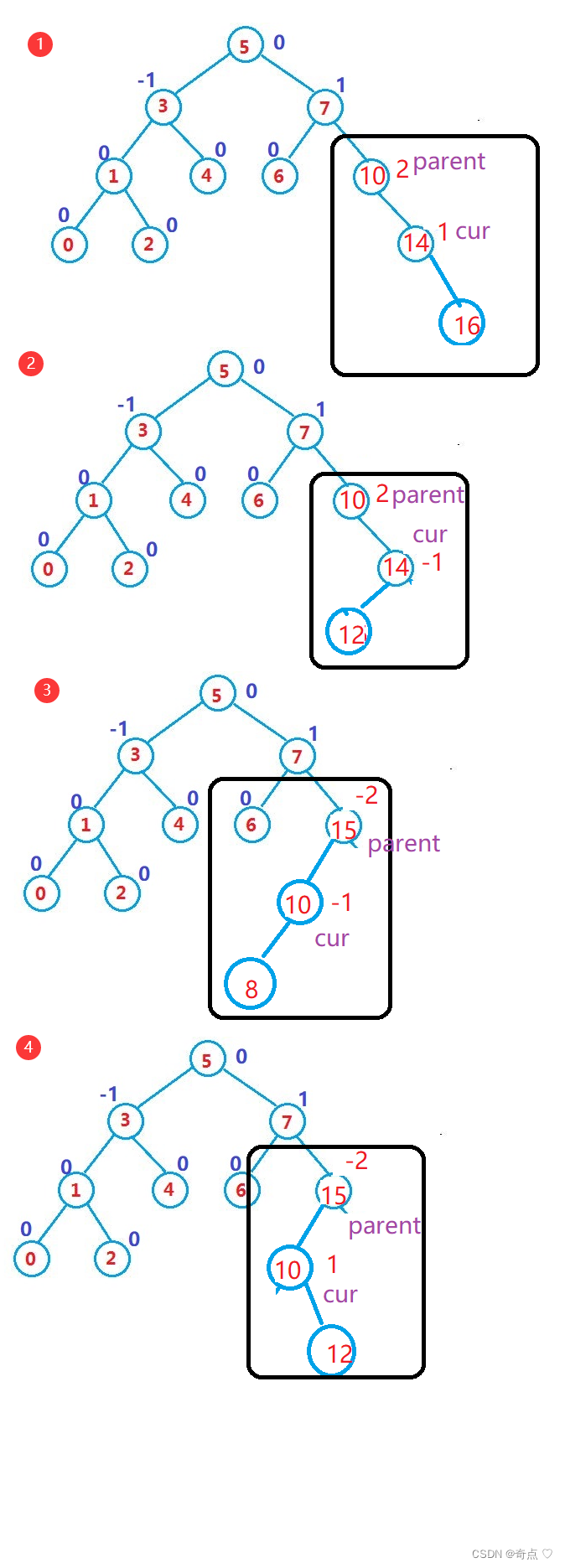
else if (parent->_bf == 2 || parent->_bf == -2){// 进行旋转处理 -- 1、让这颗子树平衡 2、降低这颗子树的高度if(parent->_bf==2&&cur->_bf==1){ }else if (parent->_bf == 2 && cur->_bf == -1){}else if (parent->_bf == -2 && cur->_bf == 1){}else if (parent->_bf == -2 && cur->_bf == -1){}else{assert(false);//有可能不会出现上面的情况,出现大问题了,立马断死}}
左单旋

代码怎么写呢?
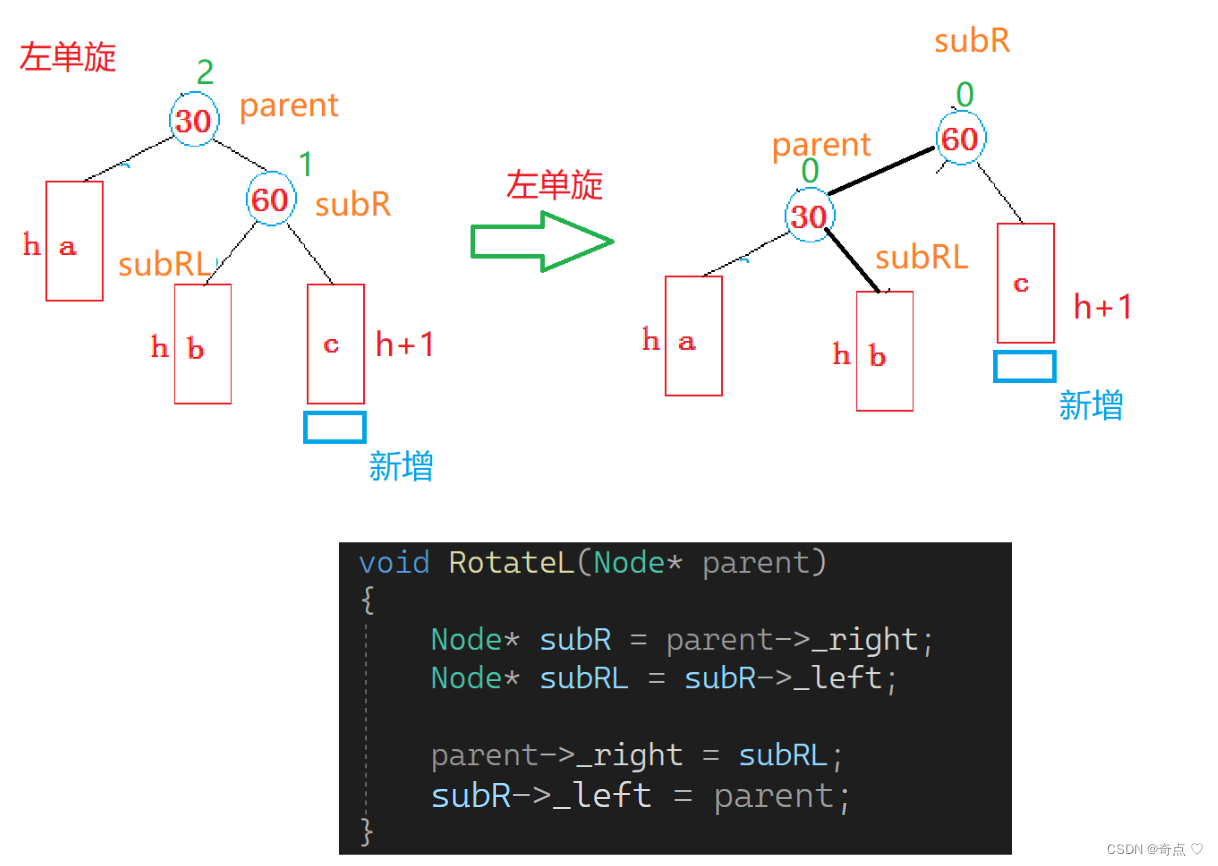 是不是感觉这样就链接上了,其实不对的,每个节点的父亲也要更新的
是不是感觉这样就链接上了,其实不对的,每个节点的父亲也要更新的
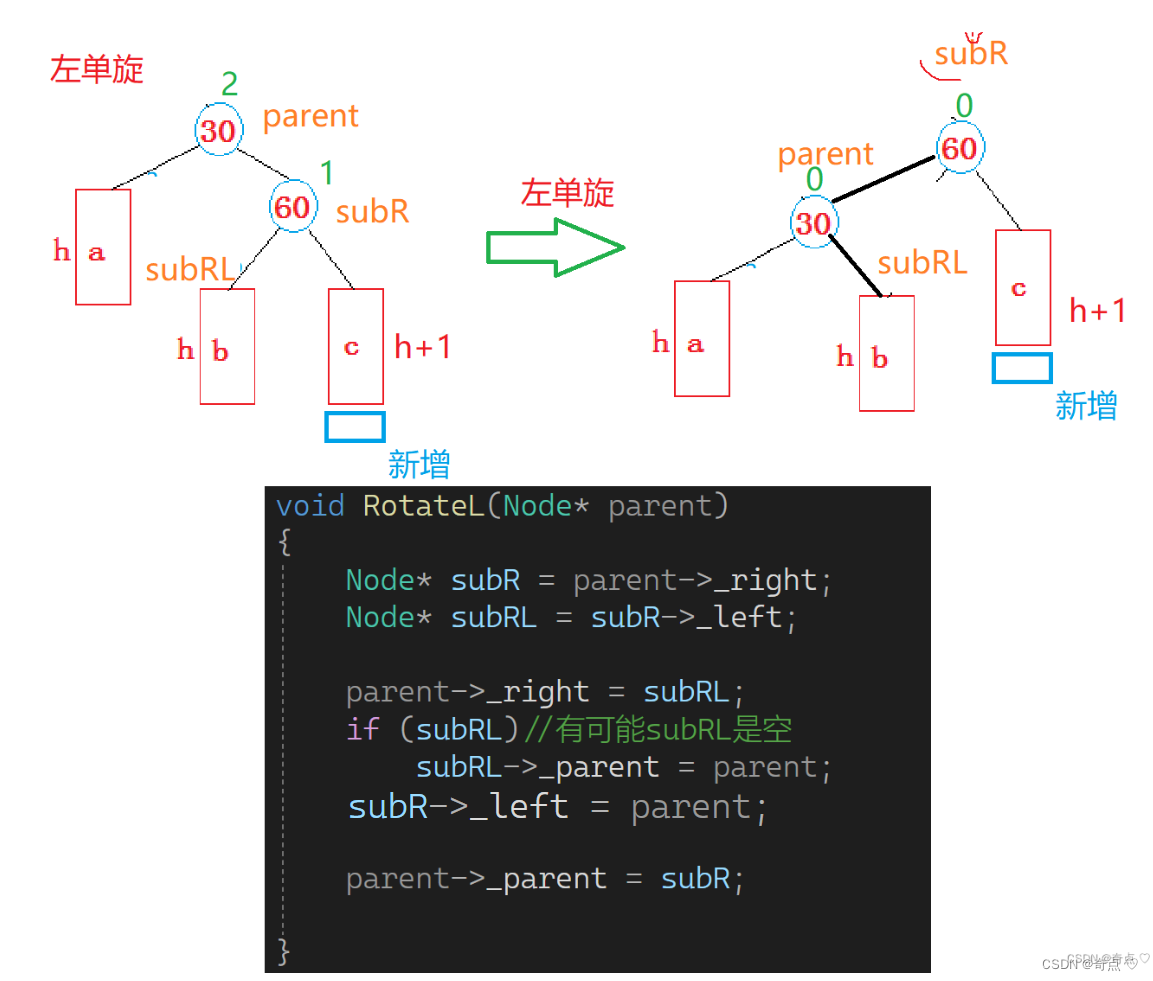 你以为又结束了吗?
你以为又结束了吗?
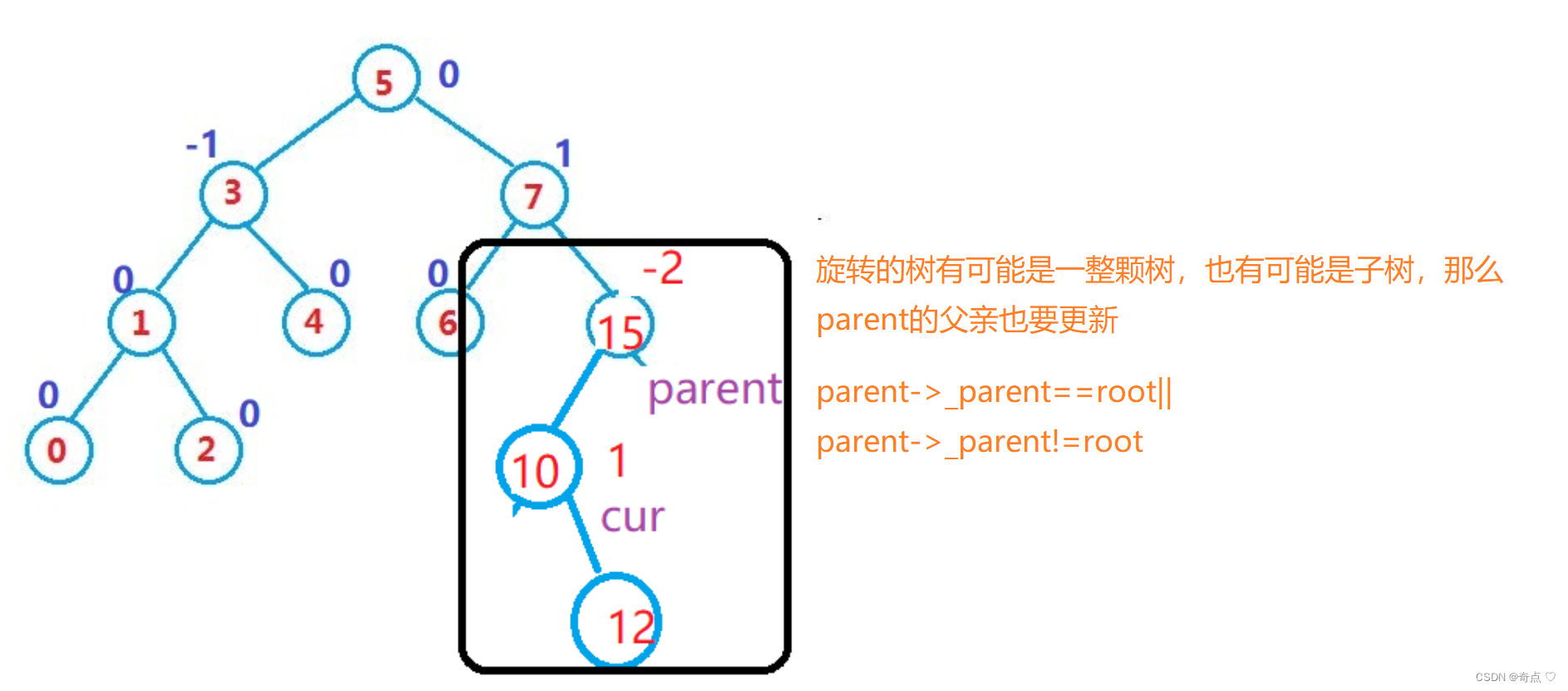
protected:void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)//有可能subRL是空subRL->_parent = parent;//记录父亲的父亲节点Node* pparent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}//更新平衡因子parent->_bf = subR->_bf = 0; }总结:更新节点指向是一定要更新他的父亲节点的指向
右单旋
和左单旋是类似的,读者可以模仿上面来分析,自己把它写出来
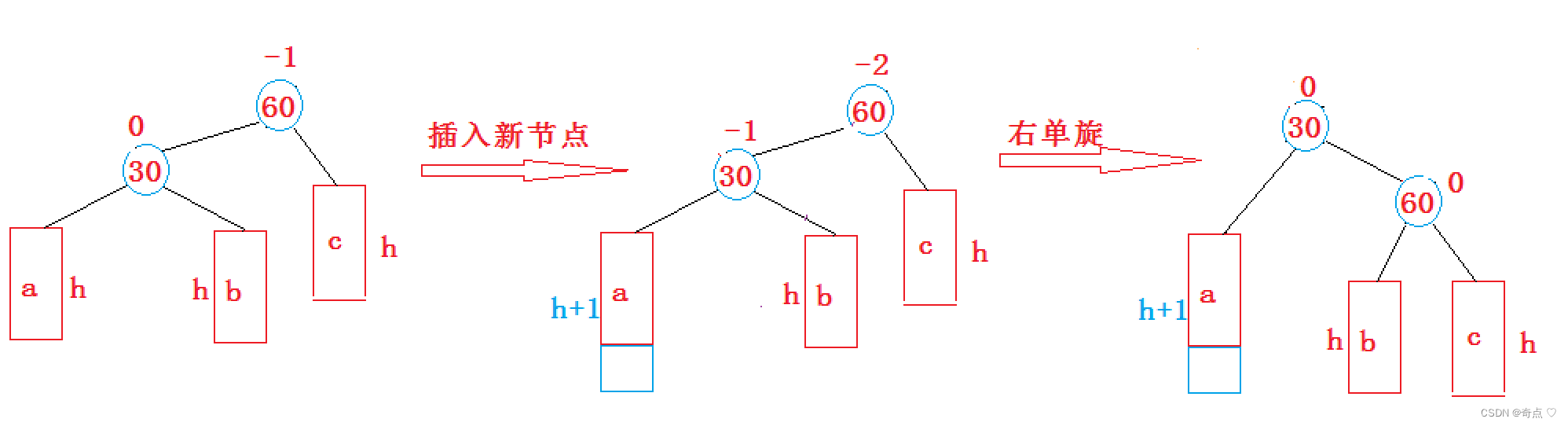
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subR->_right;parent->_left = subLR;if (subLR) //有可能subLR是空subLR->_parent = parent;//记录父亲的父亲节点Node* pparent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}//更新平衡因子parent->_bf = subL->_bf = 0;}右左双旋
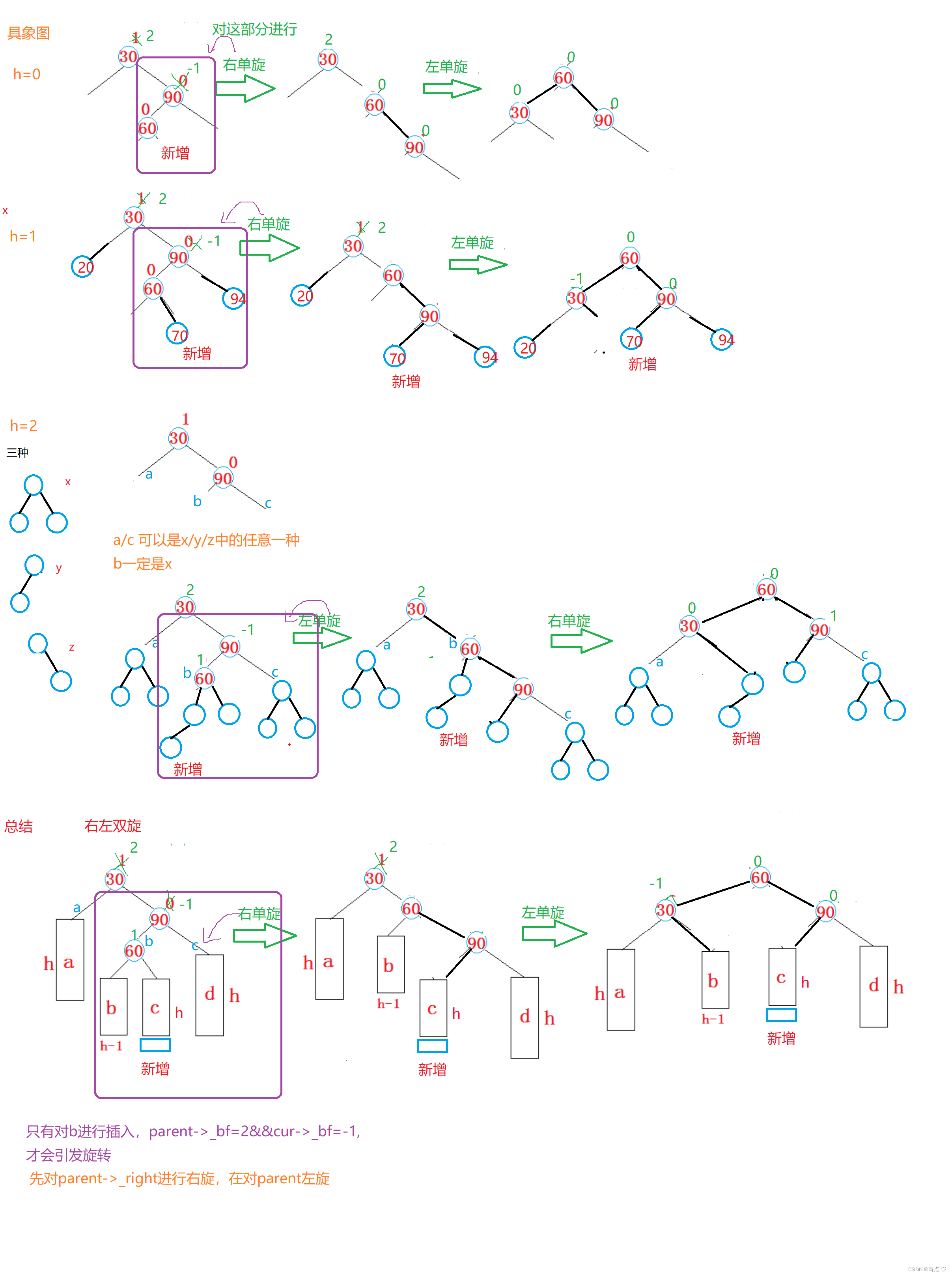
代码怎么写呢?
我们可以对单旋进行复用
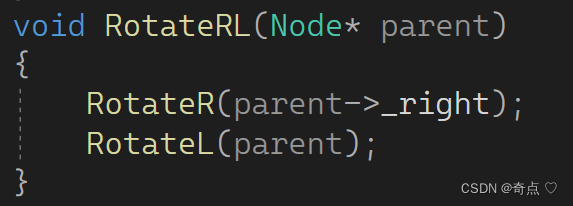
这样就可以了吗?不是,单旋会把平衡因子都置为0,所以还要更新平衡因子
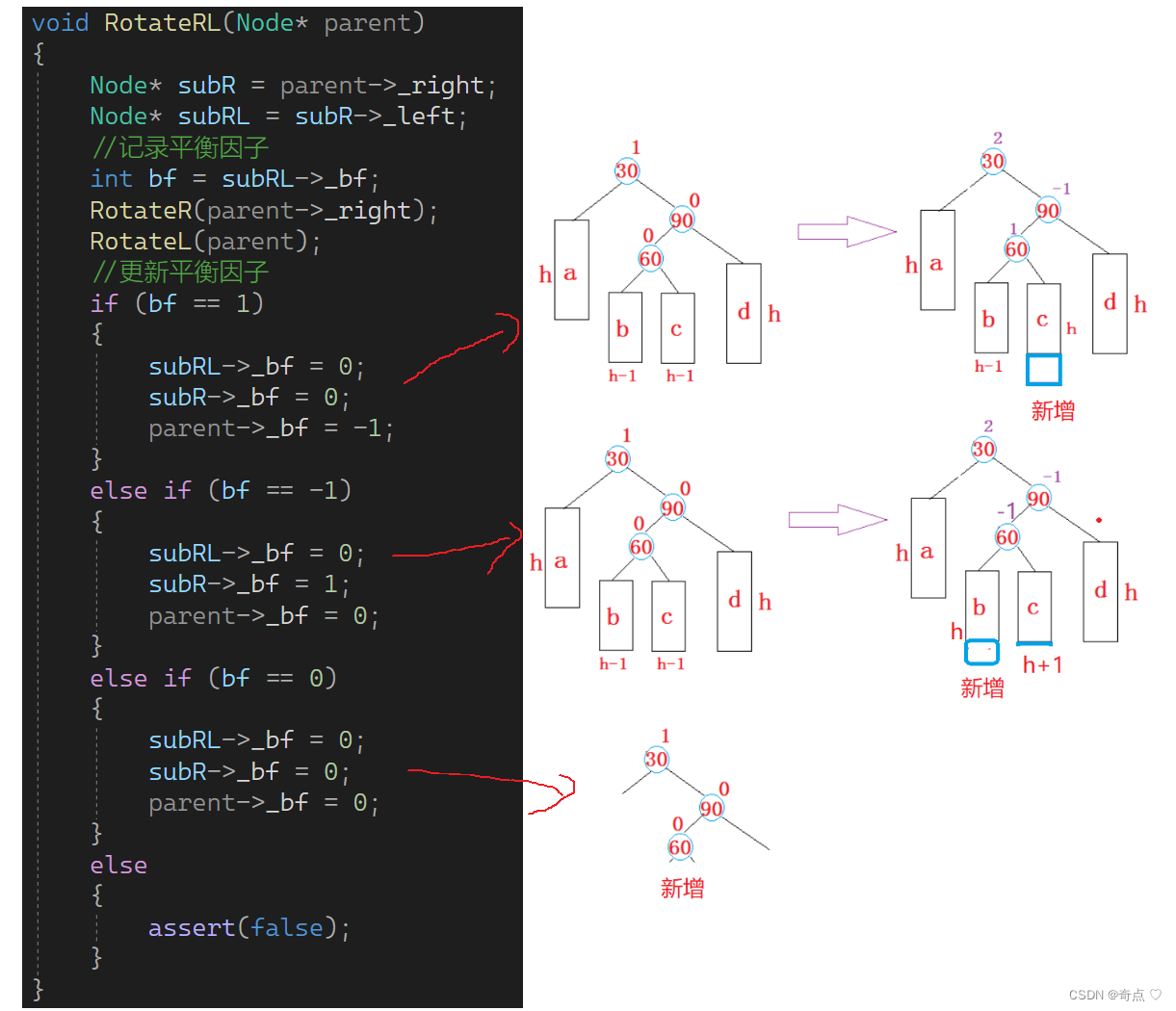
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//记录平衡因子int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//更新平衡因子if (bf == 1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 0;subR->_bf = 1;parent->_bf = 0;}else if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}}左右双旋
类似的,读者自行分析
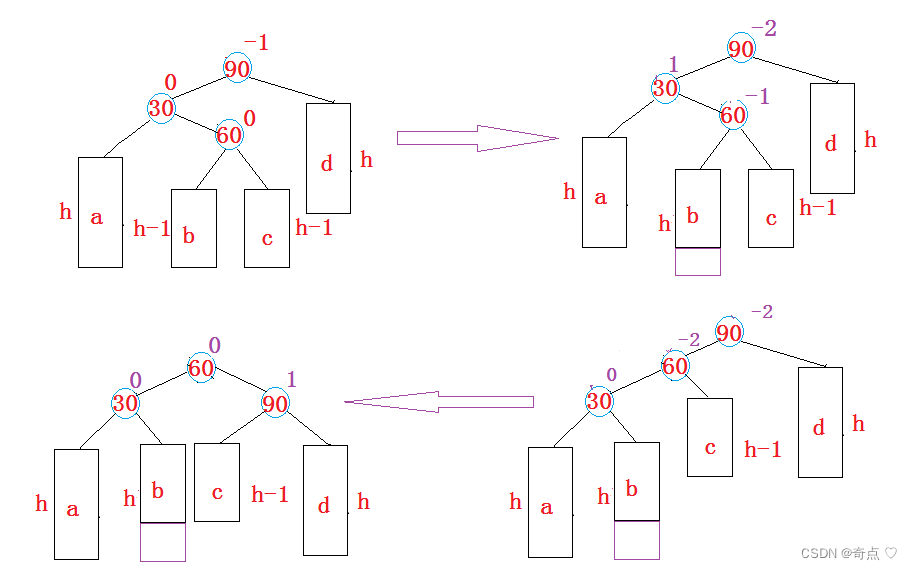
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf== 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}}else if (parent->_bf == 2 || parent->_bf == -2){// 进行旋转处理 -- 1、让这颗子树平衡 2、降低这颗子树的高度if(parent->_bf==2&&cur->_bf==1){ RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else{assert(false);//有可能不会出现上面的情况,出现大问题了,立马断死}break;//直接跳出}3.AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
1. 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子),节点的平衡因子是否计算正确
第一点很简单啦!!!!
void Inorder(){_Inorder(_root);cout << endl;}
void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ' ';_Inorder(root->_right);}怎么验证平衡树呢?
bool Isbalance(){return _Isbalance(_root);}bool _Isbalance(Node* root){if (root == nullptr)return true;int leftH = _Height(root->_left);int rightH = _Height(root->_right);//用于快速判断哪个节点错误if (rightH - leftH != root->_bf){cout << root->_kv.first << "节点平衡因子异常" << endl;return false;}//不只检查本节点左右子树的平衡,其他节点的子树也要检查return abs(leftH - rightH) < 2&& _Isbalance(root->_left)&& _Isbalance(root->_right);}int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr){return 0;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH+ 1;}你们可以用这两个用例
void testAVLtree1()
{/*int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };*/int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };AVLTree<int, int> av;for (auto e : a){if (e == 14){int a = 0;}av.Insert(make_pair(e, e));}av.Inorder();cout << av.Isbalance()<<endl;
}也要用随机数验证
void testAVLtree2()
{srand(time(0));const size_t N = 500000;AVLTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.Isbalance() << endl;cout << t.Height() << endl;
}
这两个都过了说明你的树就没问题了
相关文章:

AVL树的旋转
目录 1.平衡因子 2.旋转 a.节点定义 b.插入 插入 平衡因子更新 旋转 左单旋 右单旋 右左双旋 左右双旋 3.AVL树的验证 1.平衡因子 我们知道搜索二叉树有缺陷,就是不平衡,比如下面的树 什么是搜索树的平衡?就是每个节点的左右子树的…...
)
C++(动态规划之拆分整数)
其实我交上去都有点似懂非懂 题目:(343. 整数拆分 - 力扣(LeetCode)) 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 …...

unix C之环境变量
什么是环境变量 每个进程都有自己的一张环境变量表,表中的每个条目都是形如 keyvalue 的键值对形式的环境变量。 进程可以通过环境变量访问计算机资源。 在终端下输入env命令,可以查看环境变量列表。 通过echo $name 可以查看某个环境变量的值。 环…...

Flutter实战记录-协作开发遇到的问题
一.前言 Android项目使用了混合架构,部分模块使用Flutter进行开发。在电脑A上开发的项目提交到git仓库,电脑B拉取后进行操作,遇到两个问题,特此做一下记录; 二.问题A Settings file ‘D:\xxx\settings.gradle’ line…...

Linux 安装JDK和Idea
安装JDK 下载安装包 下载地址: Java Downloads | Oracle (1) 使用xshell 上传JDK到虚拟机 (2) 移动JDK 包到/opt/environment cd ~ cd /opt sudo mkdir environment # 在 /opt下创建一个environment文件夹 ls# 复制JDK包dao /opt/environment下 cd 下载 ls jd…...

c#绘制渐变色的Led
项目场景: c#绘制渐变色的button using System; using System.ComponentModel; using System.Drawing; using System.Drawing.Drawing2D; using System.Windows.Forms; using static System.Windows.Forms.AxHost;namespace WindowsFormsApp2 {public class Gradie…...
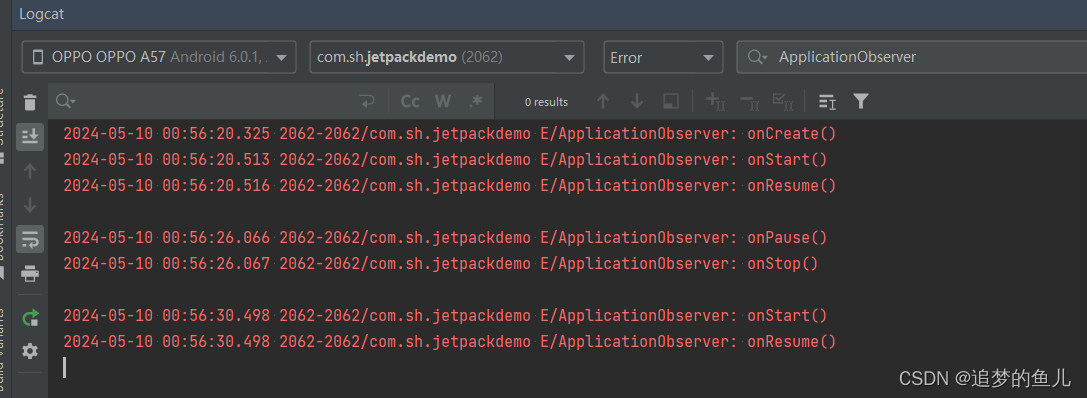
LifeCycle之ProcessLifeCycleOwner
问题:想要知道应用程序当前处在前台、后台、或从后台回到前台,想要知道应用的状态, LifeCycle提供了ProcessLifeCycleOwner的类,方便我们知道整个应用程序的生命周期情况 ProcessLifeCycleOwner 使用方法 1.首先添加依赖 imple…...

C++ | Leetcode C++题解之第79题单词搜索
题目: 题解: class Solution { public:bool exist(vector<vector<char>>& board, string word) {rows board.size();cols board[0].size();for(int i 0; i < rows; i) {for(int j 0; j < cols; j) {if (dfs(board, word, i, …...

如何通过PHP语言实现远程控制空调
如何通过PHP语言实现远程控制空调呢? 本文描述了使用PHP语言调用HTTP接口,实现控制空调,通过不同规格的通断器,来控制不同功率的空调的电源。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备名称…...

【AI+换脸换装】从OpenAI 探索色情露骨内容领域浅聊AI换脸换装
5月9日消息,据外电报道,OpenAI 周三发布了文档草案,阐述了它希望 ChatGPT 及其其他人工智能技术如何运作。冗长的Model Spec 文件的一部分透露,该公司正在探索进军色情和其他露骨内容领域。 看完这个,心里有点惊讶&am…...
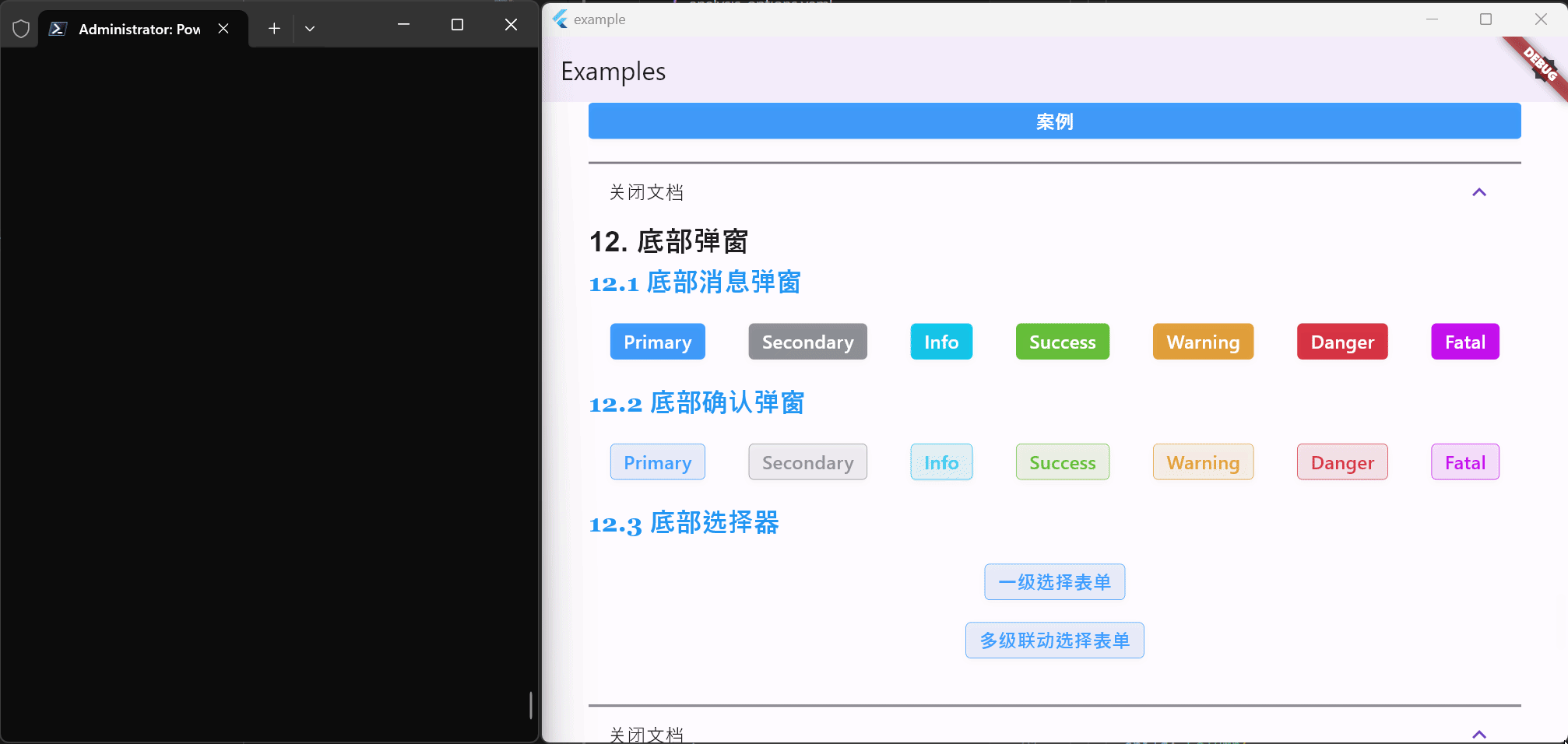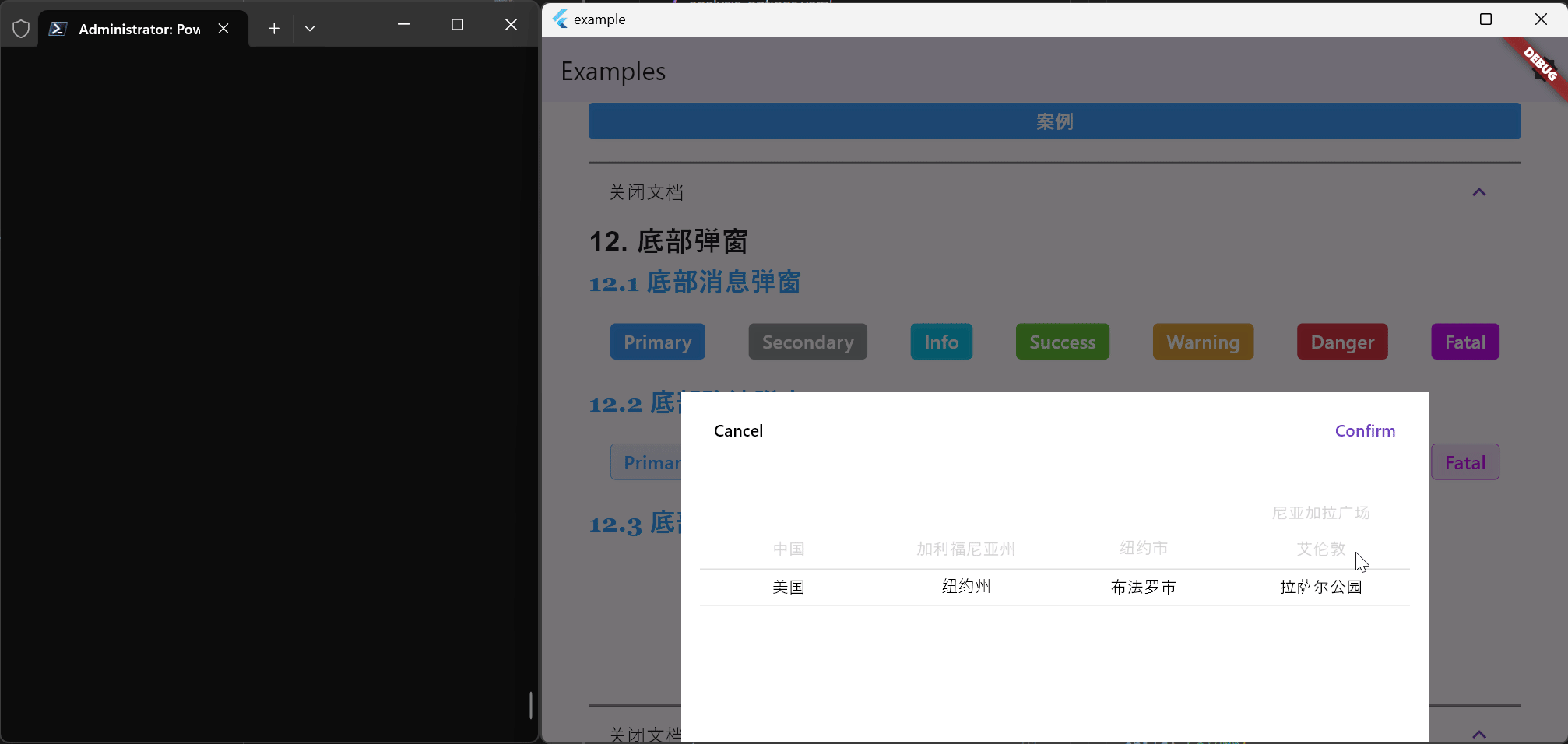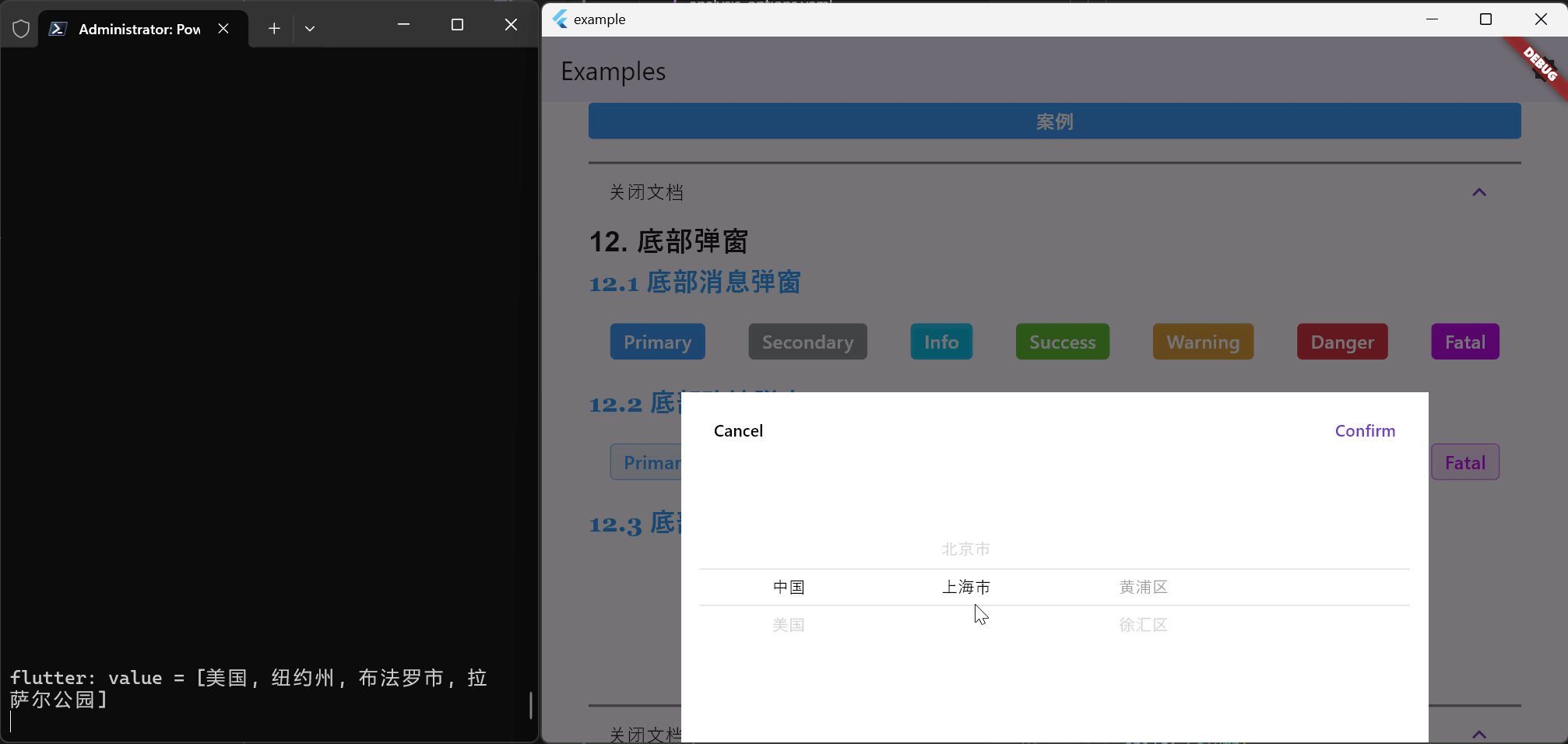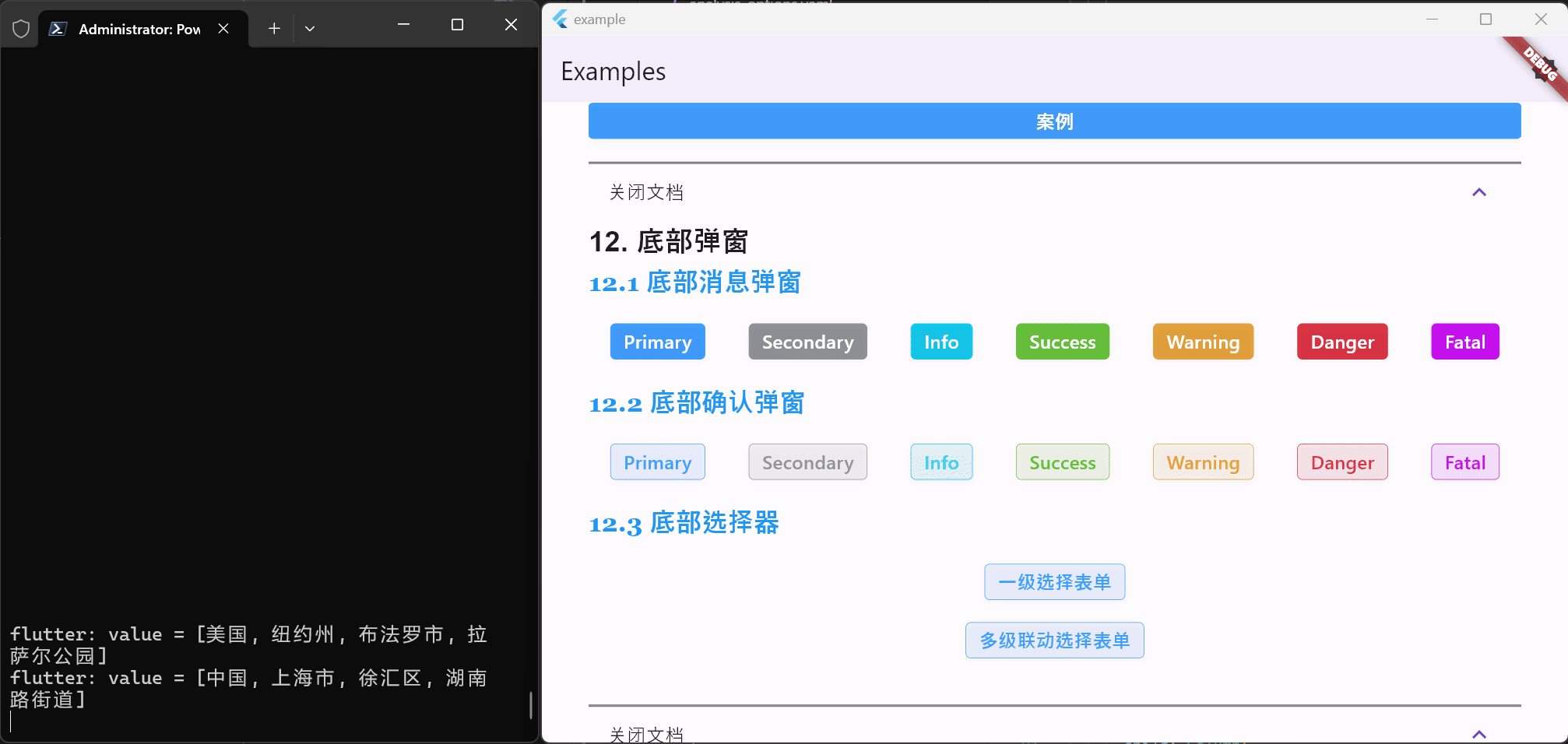
Flutter笔记:Widgets Easier组件库(13)- 使用底部弹窗
Flutter笔记 Widgets Easier组件库(13)使用底部弹窗 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this …...
RobbitMQ基本消息队列的消息发送过程
RabbitMQ: One broker to queue them all | RabbitMQ RabbitMQ官网 SpringAmqp的官方地址:Spring AMQP 代码示例:对着代码看应该能看明白 publisher:消息发送者的代码示例 package cn.itcast.mq.helloworld;import com.rabbitmq.client.Channel; import com.rabb…...

MongoDB聚合运算符:$topN
MongoDB聚合运算符:$topN 文章目录 MongoDB聚合运算符:$topN语法用法关于null和缺失值的处理BSON数据类型排序 举例查找三个得分最高的查找全部游戏中三个最高的得分基于分组key来计算参数n $topN聚合运算符返回分组中指定顺序的最前面 n个元素…...

什么是顶级域名、二级域名、三级域名?
什么是顶级域名、二级域名、三级域名? 一般域名都由两部分组成,中间用“.”隔开,一个域名是几级域名,简单的可以通过数“.”的方式来判断。 如baidu.com,它是由baidu和后缀“.com”组成,我们可以认定它是顶…...
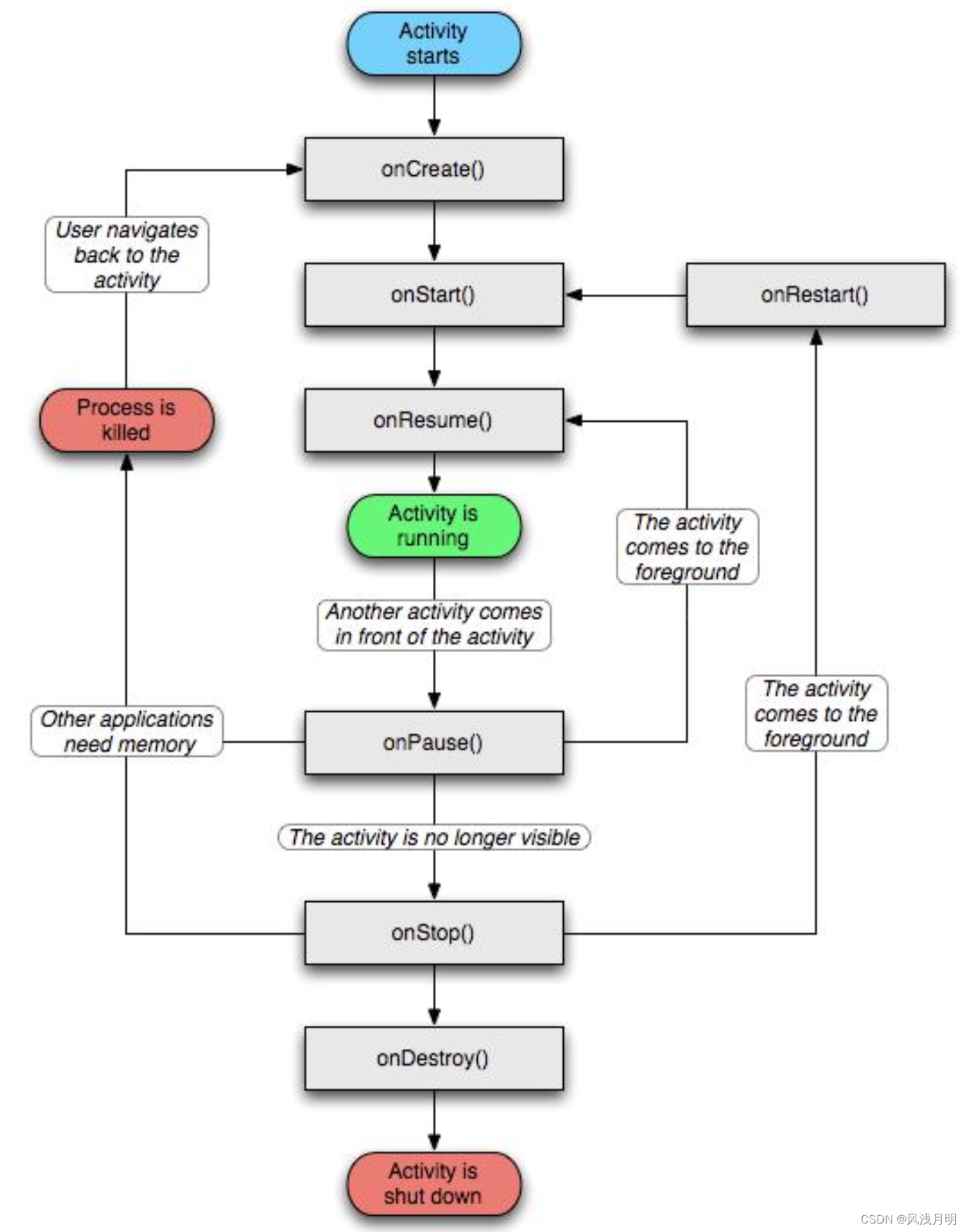
[Android]四大组件简介
在 Android 开发中,“四大组件”(Four Major Components)是指构成 Android 应用程序的四种核心组件,它们通过各自的方式与系统交互,实现应用的多样功能。这些组件是:Activity、Service、Broadcast Receiver…...
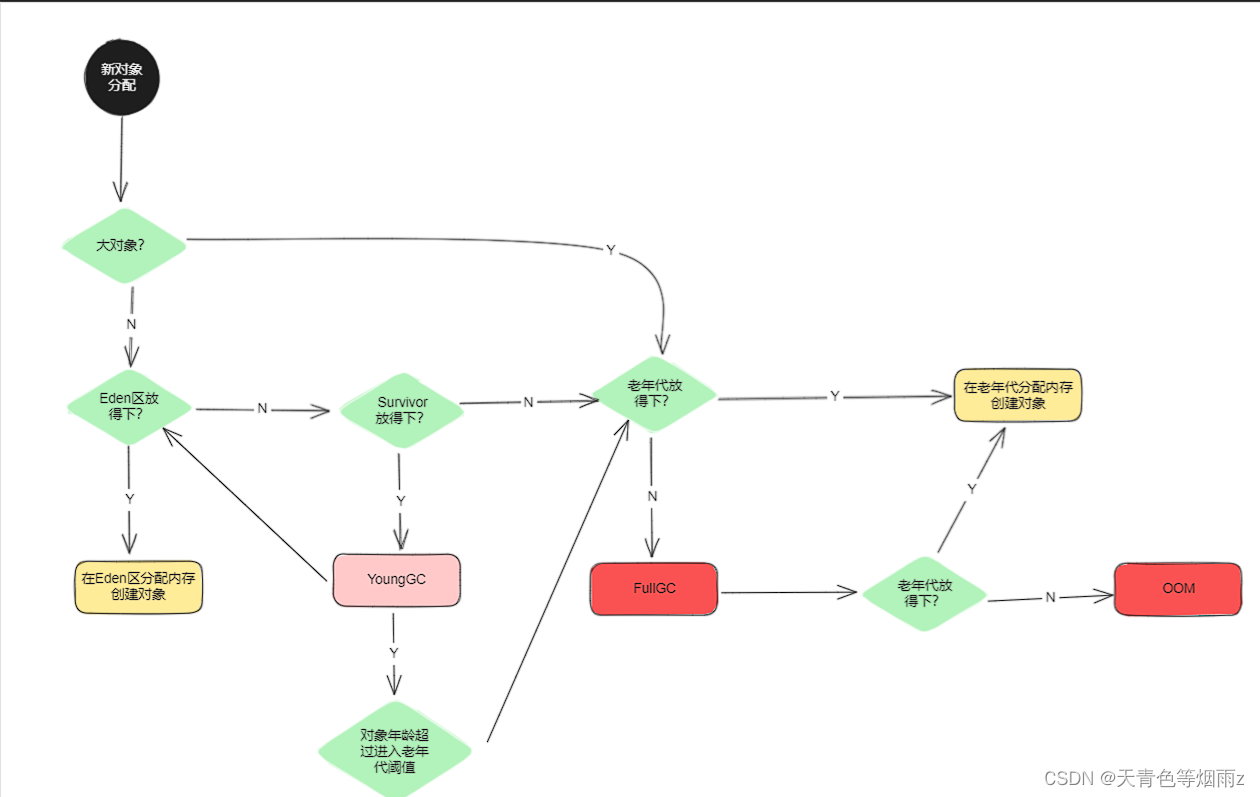
一次完整的GC流程
Java堆中内存区分 Java的堆由新生代(Young Generation)和老年代(Old Generation)组成。新生代存放新分配的对象,老年代存放长期存在的对象。 新生代(Young)由年轻区(Eden&a…...
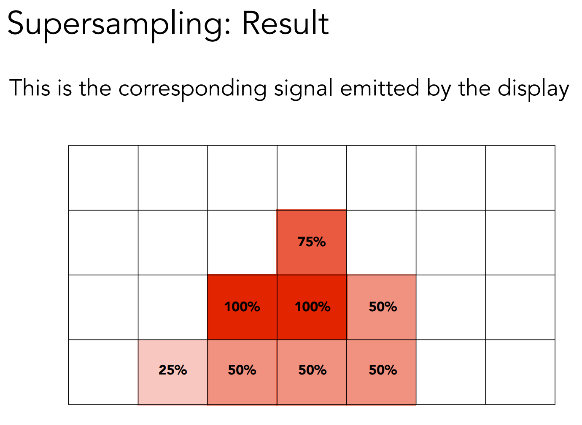
GAME101-Lecture06学习
前言 上节课主要讲的是三角形的光栅化。重要的思想是要利用像素的中心对三角形可见性的函数进行采样。 这节课主要就是反走样。 课程链接:Lecture 06 Rasterization 2 (Antialiasing and Z-Buffering)_哔哩哔哩_bilibili 反走样引入 通过采样,得到…...
等级考试试卷(二级))
202203青少年软件编程(Python)等级考试试卷(二级)
第 1 题 【单选题】 关于Python中的列表,下列描述错误的是?( ) A :列表是Python中内置可变序列,是若干元素的有序集合; B :列表中的每一个数据称为“元素”; C :在Python中,一个列表中的数据类型可以各不相同; D :可以使用s[1]来获取列表s的第一个元素。 正确答案…...

带有-i选项的sed命令在Linux上执行成功,但在MacOS上失败了
问题: 我已经成功地使用以下 sed 命令在Linux中搜索/替换文本: sed -i s/old_string/new_string/g /path/to/file然而,当我在Mac OS X上尝试时,我得到: command i expects \ followed by text我以为我的Mac运行的是…...

[Linux_IMX6ULL驱动开发]-GPIO子系统和Pinctrl子系统
目录 Pinctrl子系统的概念 GPIO子系统的概念 定义自己的GPIO节点 GPIO子系统的函数 引脚号的确定 基于GPIO子系统的驱动程序 驱动程序 设备树修改 之前我们进行驱动开发的时候,对于硬件的操作是依赖于ioremap对寄存器的物理地址进行映射,以此来达…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
