C++|二叉搜索树
一、二叉搜索树的概念
二叉搜索树又称为二叉排序树,它或者是一颗空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根结点的值
- 它的每一颗子树都是搜索二叉树,满足该三条规则。
可以简单的总结一下,整个左子树的值比根小,整个右子树的值比根大,且每一颗子树符合该规则
例如: 二叉搜索树 非二叉搜索树,3的左子树大于根
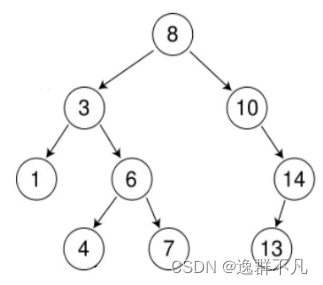
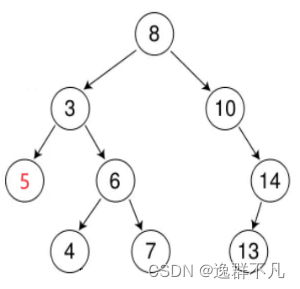
二、二叉搜索树的实现
二叉搜索树的实现,首先得创建一个节点类,用来存放数据,接着再创建树的框架,用来管理节点的插入,查找,删除等操作 。
2.1节点创建
实现成模板,可以存放各种类型的数据,为了让节点与节点之间关联起来,所以有两个指针,_left,_right分别指向左右节点 ,_data则是存放具体值。构造函数则是初始化节点的内容
template<class T>struct BSTnode{BSTnode(const T& data = T())//初始化节点内容:_left(nullptr), _right(nullptr), _data(data){}BSTnode<T>* _left;BSTnode<T>* _right;T _data;};2.2构造与拷贝构造
创建节点后,接着创建树,用来管理节点,首先就是实现构造函数对节点进行初识化,然后实现拷贝构造,拷贝构造需要将一颗树的所有节点值全拷贝过来,故可以采用递归的方式实现。
template<class T>class BSTree{typedef BSTnode<T> Node;typedef Node* PNode;public:BSTree():_Root(nullptr){}BSTree(const BSTree<T>& t){_Root = CopyNode(t._Root);}PNode CopyNode(PNode Root){if (Root == nullptr){return nullptr;}PNode node = new Node;//创建新结点,存放节点值node->_data = Root->_data;//拷贝节点值node->_left = CopyNode(Root->_left);//链接左节点node->_right = CopyNode(Root->_right);//链接右节点return node;}private:PNode _Root;//采用节点指针};
2.3插入(循环版本&&递归版本)
接下来进行具体的管理节点,首先就是节点的插入,思想的实现可以分为两个步骤:
1.树为空,则直接新增节点,赋值给_Root 指针
2.树不为空,按二叉树的性质搜索查找插入位置,插入新节点
3.若出现相同的值则不插入
二叉搜索树需要不断的进行比较,最终插入,所以其实现可以用循环和递归实现,为了表示是否插入成功,所以使其需要返回值。
例如:插入新节点,16、0。根据二叉搜索树的性质,进行比较,插入
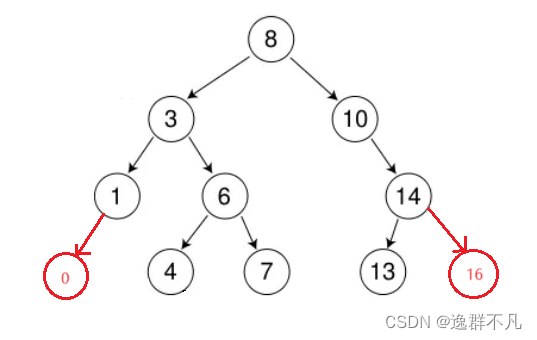
循环版本
bool Insert(const T& data){//空树,新增节点if (_Root == nullptr){_Root = new Node;_Root->_data = data;return true;}//不为空,进行比较PNode cur = _Root;PNode parent = nullptr;//存放cur的上一个位置while (cur){parent = cur;if (data < cur->_data)//小于根节点,则往左子树{cur = cur->_left;}else if (data > cur->_data)//大于根节点,则往右子树{cur = cur->_right;}else//有相同值,返回假{return false;}}//循环结束,说明找到了要插入的位置,但cur为空//而parent是cur的上一个位置,所以用parent比较插入if (data < parent->_data){PNode node = new Node;node->_data = data;parent->_left = node;}else if (data > parent->_data){PNode node = new Node;node->_data = data;parent->_right = node;}return true;}递归版本
bool Insert(const T& data){return _Insert(_Root,data);}bool _Insert(PNode& Root,const T& data){//为空,新增节点,直接返回,或者,不为空在最后插入节点,返回if (Root == nullptr){//PNode node = new Node;//Root = node;//node->_data = data;Root = new Node(data);return true;}if (data < Root->_data)//小于根节点,往左子树return _Insert(Root->_left, data);else if (data > Root->_data)return _Insert(Root->_right, data);//大于根节点,往右子树elsereturn false;}2.4查找(循环版本&&递归版本)
同理,查找需要不断进行比较,依然可以通过循化和递归实现。 查找成功,返回当前位置指针,否则返回nullptr
循环版本
PNode Find(const T& data){//树空if (_Root == nullptr){return nullptr;}//不为空PNode cur = _Root;while (cur){if (data < cur->_data){cur = cur->_left;}else if (data > cur->_data){cur = cur->_right;}else{return cur;//找到,返回该位置指针}}return nullptr;}
递归版本
PNode Find(const T& data){return _Find(_Root,data);}PNode _Find(PNode Root,const T& data){if (Root == nullptr){return nullptr;}if (data < Root->_data){return _Find(Root->_left, data);}else if (data > Root->_data){return _Find(Root->_right, data);}else{return Root;}}
2.5删除(循环版本&&递归版本)
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的节点可能分下面四种情况:
1.要删除的结点无孩子结点
2.要删除的结点只有左孩子
3.要删除的结点只有右孩子
4.要删除的结点有左、右孩子结点
①要删除的节点无孩子、只有左孩子、右孩子可以归类为一种情况。 都是让删除节点的父亲指向删除节点的孩子即可。
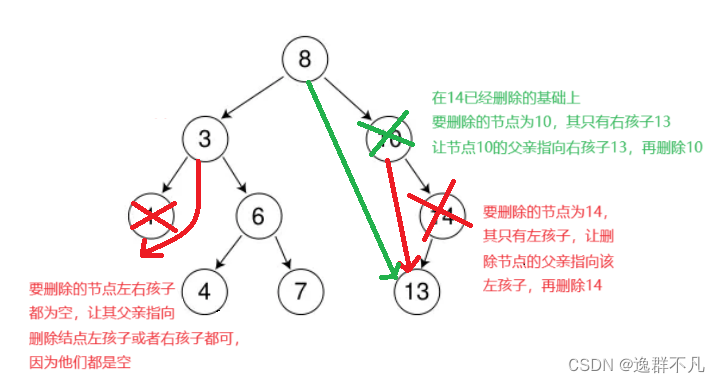
②要删除的节点有左右孩子可以归类为一种情况。
删除该节点时,其还有左右孩子,所以导致的问题是得重新排序链接。为了保持二叉搜索树的结构,可以采用替换删除法:找一个替换我的节点,交换值,转换删除他。那么其有两种删除方式。
a.找删除结点的左子树的最大节点进行交换删除(左子树最右节点)
b.找删除结点的右子树的最小节点进行交换删除(右子树最左节点)
解释:因为左子树中的最大节点比删除结点的左孩子大、右孩子小。右子树中的最小节点也比删除结点的左孩子大、右孩子小。那么交换删除,依然满足二叉搜索树的结构。
在代码实现中,就采用第二种,找右子树的最小节点。
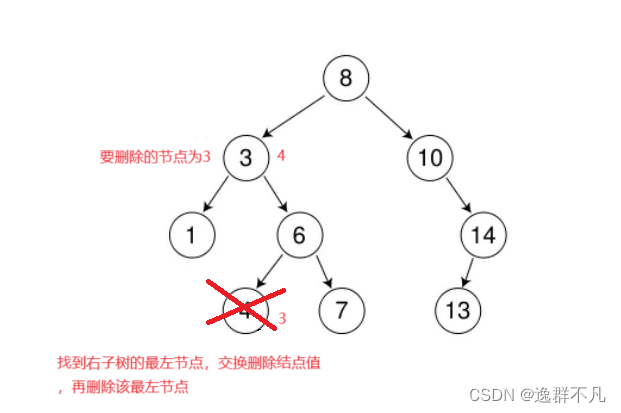
循环版本
bool Erase(const T& data){if (_Root == nullptr)//树为空,返回faslereturn false;PNode cur = _Root;PNode parent = _Root;//跟踪cur,始终保持为cur的父亲//查找要删除节点位置while (cur){if (data < cur->_data){parent = cur;cur = cur->_left;}else if (data > cur->_data){parent = cur;cur = cur->_right;}elsebreak;//找到跳出}//未找到,返回FALSEif (cur == nullptr)return false;//要删除的节点只有右孩子if (cur->_left == nullptr){//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_right;}//判断该删除结点是父亲的左孩子还是右孩子if (data < parent->_data)//是父亲的左孩子{parent->_left = cur->_right;}else if(data > parent->_data)//是父亲的右孩子{parent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//要删除的结点只有左孩子{//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_left;}//判断该删除结点是父亲的左孩子还是右孩子if (data < parent->_data)//是父亲的左孩子{parent->_left = cur->_left;}else if(data > parent->_data)//是父亲的右孩子{parent->_right = cur->_left;}delete cur;}else//跟右子树的最左节点(即最小节点)进行交换,再删除{PNode pparent = cur;//跟踪parentparent = cur->_right;//先指向右子树的根节点//找右子树最左节点while (parent->_left){pparent = parent;parent = parent->_left;}//交换,重新链接,删除cur->_data = parent->_data;if (cur == pparent){pparent->_right = parent->_right;}else{pparent->_left = parent->_right;}delete parent;}return true;//删除成功,返回true}
递归版本
bool Erase(const T& data){return _Erase(_Root, data);}bool _Erase(PNode& Root,const T& data)//Root采用引用,引用的是上一个Root->_left。目的是,当找到删除结点,其只有一个孩子或者无孩子,就可以让删除结点的父亲指向孩子,该父亲就是当前Root,引用的是上一个Root->_left。即PNode& Root= Root->_left{if (Root == nullptr){return false;}//查找删除结点if (data < Root->_data){_Erase(Root->_left, data);//小于查找节点,到左子树查找}else if (data > Root->_data){_Erase(Root->_right, data);//大于查找节点,到右子树查找}else//找到删除结点,判断其是否有孩子,进行交换删除{PNode cur = Root;//要删除的节点只有右孩子if (Root->_left == nullptr){ Root = Root->_right;//链接右孩子}else if (Root->_right == nullptr)//要删除的节点只有左孩子{Root = Root->_left;//链接左孩子}else//要删除的节点有左右孩子,采用替换法删除{cur = Root->_right;//寻找最左节点while (cur->_left){cur = cur->_left;}//交换swap(Root->_data,cur->_data);return _Erase(Root->_right, data);//转换成在删除结点的右子树中查找交换后要删除的节点,因为交换后的删除的节点其要么只有一个孩子要么没有孩子}delete cur;cur = nullptr;return true;}}2.6析构
void Delete(PNode Root)//后序递归删除{if (Root == nullptr)return;Delete(Root->_left);Delete(Root->_right);delete Root;}~BSTree(){if (_Root == nullptr)delete _Root;Delete(_Root);}2.7总代码(循环版本&&递归版本)
循环版本:
//BSTeee-key.h
#include <iostream>
using namespace std;namespace bit
{template<class T>struct BSTnode{BSTnode(const T& data = T()):_left(nullptr), _right(nullptr), _data(data){}BSTnode<T>* _left;BSTnode<T>* _right;T _data;};template<class T>class BSTree{typedef BSTnode<T> Node;typedef Node* PNode;public:BSTree():_Root(nullptr){}BSTree(const BSTree<T>& t){_Root = CopyNode(t._Root);}PNode CopyNode(PNode Root){if (Root == nullptr){return nullptr;}PNode node = new Node;node->_data = Root->_data;node->_left = CopyNode(Root->_left);node->_right = CopyNode(Root->_right);return node;}//插入bool Insert(const T& data){//空树if (_Root == nullptr){_Root = new Node;_Root->_data = data;return true;}//不为空PNode cur = _Root;PNode parent = nullptr;while (cur){parent = cur;if (data < cur->_data){cur = cur->_left;}else if (data > cur->_data){cur = cur->_right;}else{return false;}}if (data < parent->_data){PNode node = new Node;node->_data = data;parent->_left = node;}else if (data > parent->_data){PNode node = new Node;node->_data = data;parent->_right = node;}return true;}//查找PNode Find(const T& data){//树空if (_Root == nullptr){return nullptr;}//不为空PNode cur = _Root;while (cur){if (data < cur->_data){cur = cur->_left;}else if (data > cur->_data){cur = cur->_right;}else{return cur;}}return nullptr;}//删除--替换删除法bool Erase(const T& data){if (_Root == nullptr)//树为空,返回faslereturn false;PNode cur = _Root;PNode parent = _Root;//跟踪cur,始终保持为cur的父亲//查找要删除节点位置while (cur){if (data < cur->_data){parent = cur;cur = cur->_left;}else if (data > cur->_data){parent = cur;cur = cur->_right;}elsebreak;//找到跳出}//未找到,返回FALSEif (cur == nullptr)return false;//要删除的节点只有右孩子if (cur->_left == nullptr){//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_right;}//判断该删除结点是父亲的左孩子还是右孩子if (data < parent->_data)//是父亲的左孩子{parent->_left = cur->_right;}else if(data > parent->_data)//是父亲的右孩子{parent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//要删除的结点只有左孩子{//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_left;}//判断该删除结点是父亲的左孩子还是右孩子if (data < parent->_data)//是父亲的左孩子{parent->_left = cur->_left;}else if(data > parent->_data)//是父亲的右孩子{parent->_right = cur->_left;}delete cur;}else//跟右子树的最左节点(即最小节点)进行交换,再删除{PNode pparent = cur;//跟踪parentparent = cur->_right;//先指向右子树的根节点//找右子树最左节点while (parent->_left){pparent = parent;parent = parent->_left;}//交换,重新链接,删除cur->_data = parent->_data;if (cur == pparent){pparent->_right = parent->_right;}else{pparent->_left = parent->_right;}delete parent;}return true;//删除成功,返回true}void Delete(PNode Root){if (Root == nullptr)return;Delete(Root->_left);Delete(Root->_right);delete Root;}~BSTree(){if (_Root == nullptr)delete _Root;Delete(_Root);}void _InOrder(PNode Root){if (Root == nullptr)return;_InOrder(Root->_left);cout << Root->_data << " ";_InOrder(Root->_right);}void InOrder(){_InOrder(_Root);cout << endl;}private:PNode _Root;//采用节点指针};void BSTreetest(){BSTree<int> t;int a[] = { 8,3,1,10,6,4,7,14,13 };for (int i = 0; i < 9; i++){t.Insert(a[i]);}t.Erase(6);BSTree<int> ts(t);ts.InOrder();}}测试:
test.cpp
#include "BSTeee-key.h"
int main()
{bit::BSTreetest();return 0;
}输出结果:

递归版本:
//BSTeee-key2.h
#include <iostream>
using namespace std;namespace bit
{template<class T>struct BSTnode{BSTnode(const T& data = T()):_left(nullptr), _right(nullptr), _data(data){}BSTnode<T>* _left;BSTnode<T>* _right;T _data;};template<class T>class BSTree{typedef BSTnode<T> Node;typedef Node* PNode;public:BSTree():_Root(nullptr){}BSTree(const BSTree<T>& t){_Root = CopyNode(t._Root);}PNode CopyNode(PNode Root){if (Root == nullptr){return nullptr;}PNode node = new Node;node->_data = Root->_data;node->_left = CopyNode(Root->_left);node->_right = CopyNode(Root->_right);return node;}//插入bool Insert(const T& data){return _Insert(_Root,data);}bool _Insert(PNode& Root,const T& data){if (Root == nullptr){PNode node = new Node;Root = node;node->_data = data;return true;}if (data < Root->_data)return _Insert(Root->_left, data);else if (data > Root->_data)return _Insert(Root->_right, data);elsereturn false;}//查找PNode Find(const T& data){return _Find(_Root,data);}PNode _Find(PNode Root,const T& data){if (Root == nullptr){return nullptr;}if (data < Root->_data){return _Find(Root->_left, data);}else if (data > Root->_data){return _Find(Root->_right, data);}else{return Root;}}//删除--替换删除法bool Erase(const T& data){return _Erase(_Root, data);}bool _Erase(PNode& Root,const T& data){if (Root == nullptr){return false;}if (data < Root->_data){_Erase(Root->_left, data);}else if (data > Root->_data){_Erase(Root->_right, data);}else{PNode cur = Root;//要删除的节点只有右孩子if (Root->_left == nullptr){Root = Root->_right;//链接右孩子}else if (Root->_right == nullptr)//要删除的节点只有左孩子{Root = Root->_left;//链接左孩子}else//要删除的节点有左右孩子,采用替换法删除{cur = Root->_right;//寻找最左节点while (cur->_left){cur = cur->_left;}//交换swap(Root->_data, cur->_data);return _Erase(Root->_right, data);//转换成在删除结点的右子树中查找交换后要删除的节点,因为交换后的删除的节点其要么只有一个孩子要么没有孩子}delete cur;cur = nullptr;return true;}}void Delete(PNode Root){if (Root == nullptr)return;Delete(Root->_left);Delete(Root->_right);delete Root;}~BSTree(){if (_Root == nullptr)delete _Root;Delete(_Root);}void _InOrder(PNode Root){if (Root == nullptr)return;_InOrder(Root->_left);cout << Root->_data << " ";_InOrder(Root->_right);}void InOrder(){_InOrder(_Root);cout << endl;}private:PNode _Root;//采用节点指针};void BSTreetest(){BSTree<int> t;int a[] = { 8,3,1,10,6,4,7,14,13 };for (int i = 0; i < 9; i++){t.Insert(a[i]);}BSTnode<int>* p = t.Find(5);if (p == nullptr){t.Insert(5);}t.Erase(3);t.Erase(6);BSTree<int> ts(t);ts.InOrder();}
}测试:
//test.cpp
#include "BSTeee-key2.h"
int main()
{bit::BSTreetest();return 0;
}输出结果:
三、二叉搜索树的应用
3.1 k模型 && kv模型
K模型:k模型即只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值。就跟上面的代码实现一样。
比如:查询某人是否买了机票。就可以建立采用搜索二叉树,在二叉搜索树中查询该人是否存在,存在,已买,否则,未买。
kv模型:每一个关键码key,都有与之对应的值value,即<key,value>的键值对。
比如:英汉词典就是英文与中文的对应关系,通过英文了以快速找到与其对应的中文,英文单词与其对应的中文(apple,"苹果")就构成一种键值对;
3.2 KV模型的实现
对于kv模型的实现没有什么太大变化,就是在加一个模板参数,在插入节点时,给另一个模板参数也进行赋值即可。进行比较时,还是按第一个参数来比较,即按key来比较,跟value无关。
//BSTree.h
#include <iostream>
#include <string>
using namespace std;namespace bit
{template<class K,class V>struct BSTnode{BSTnode(const K& key = K(),const V& value= V()):_left(nullptr), _right(nullptr), _key(key),_value(value){}BSTnode<K, V>* _left;BSTnode<K, V>* _right;K _key;V _value;};template<class K, class V>class BSTree{public:typedef BSTnode<K, V> Node;typedef Node* PNode;public:BSTree():_Root(nullptr){}//插入bool Insert(const K& key, const V& value){//空树if (_Root == nullptr){_Root = new Node;_Root->_key = key;_Root->_value = value;return true;}//不为空PNode cur = _Root;PNode parent = nullptr;while (cur){parent = cur;if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return false;}}if (key < parent->_key){PNode node = new Node;node->_key = key;node->_value = value;parent->_left = node;}else if (key > parent->_key){PNode node = new Node;node->_key = key;node->_value = value;node->_value = value;parent->_right = node;}return true;}//查找PNode Find(const K& key){//树空if (_Root == nullptr){return nullptr;}//不为空PNode cur = _Root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;}}return nullptr;}//删除--替换删除法bool Erase(const K& key){if (_Root == nullptr)return false;PNode cur = _Root;PNode parent = nullptr;//查找要删除节点位置while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}elsebreak;}//未找到,返回FALSEif (cur == nullptr)return false;//要删除的节点只有右孩子if (cur->_left == nullptr){//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_right;}//判断该删除结点是父亲的左孩子还是右孩子if (key < parent->_key)//是父亲的左孩子{parent->_left = cur->_right;delete cur;}else if(key > parent->_key)//是父亲的右孩子{parent->_right = cur->_right;delete cur;}}else if (cur->_right == nullptr)//要删除的节点只有右孩子{//要删除的节点是根节点,更新根节点,再删除if (cur == _Root){_Root = cur->_right;}//判断该删除结点是父亲的左孩子还是右孩子if (key < parent->_key)//是父亲的左孩子{parent->_left = cur->_left;delete cur;}else if(key > parent->_key)//是父亲的右孩子{parent->_right = cur->_left;delete cur;}}else//跟右子树的最左节点(即最小节点)进行交换,再删除{PNode pparent = cur;parent = cur->_right;//找最左节点while (parent->_left){pparent = parent;parent = parent->_left;}//交换删除cur->_key = parent->_key;if (cur == pparent){pparent->_right = parent->_right;}else{pparent->_left = parent->_right;}delete parent;}return true;}~BSTree(){if (_Root == nullptr)delete _Root;Delete(_Root);}void InOrder(){_InOrder(_Root);cout << endl;}private:void Delete(PNode Root){if (Root == nullptr)return;Delete(Root->_left);Delete(Root->_right);delete Root;}void _InOrder(PNode Root){if (Root == nullptr)return;_InOrder(Root->_left);cout << Root->_key << ":" << Root->_value << endl;;_InOrder(Root->_right);}PNode _Root;//采用节点指针};/*void BSTreetest(){BSTree<int> t;t.Insert(1);t.Insert(28);t.Insert(3);t.Insert(4);t.InOrder();}*///void BSTreetest2()//{// BSTree<int, int> t;// t.Insert(1, 1);// t.Insert(1, 1);// t.Insert(2, 1);// t.Insert(3, 1);// t.Insert(4, 1);// t.Insert(5, 1);// t.Insert(6, 1);// t.Erase(3);// t.InOrder();//}//查询单词//void BSTreetest3()//{// BSTree<string, string> dict;// //插入单词// dict.Insert("string", "字符串");// dict.Insert("binary", "二叉");// dict.Insert("search", "搜索");// dict.Insert("tree", "树");// dict.Insert("sort", "排序");// //查询单词是否在// string str;// while (cin >> str)// {// BSTnode<string, string>* ret = dict.Find(str);// if(ret == nullptr)// {// cout << "单词拼写错误,词库中没有这个单词:" << str << endl;// }// else// {// cout << str << "中文翻译:" << ret->_value << endl;// }// }//}//统计水果出现的次数void BSTreetest4(){string str[] = { "香蕉","苹果","荔枝","梨","苹果", "苹果", "西瓜","香蕉","香蕉","梨" };BSTree<string, int> countTree;for (const auto& s : str){BSTnode<string, int>* ret = countTree.Find(s);if (ret == NULL){countTree.Insert(s, 1);}else{ret->_value++;}}countTree.InOrder();}
}
测试:
//test.cpp
#include "BSTeee.h"
int main()
{bit::BSTreetest4();return 0;
}输出结果:

3.3二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个节点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是节点在二叉搜索树的深度的函数,即节点越深,则比较次数越多。
但对于同一个关键码的集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
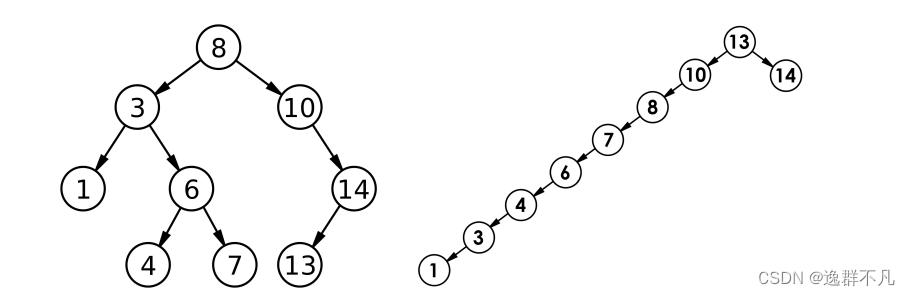
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log N
最差情况下,二叉搜索树退化为单支树,其平均比较次数为: N^2
所以问题就是,如果退化成单支树,二叉搜索树的性能就失去了。为了解决该问题,大佬们发明了了AVL树和红黑树,待后续章节进行学习。
end~
相关文章:

C++|二叉搜索树
一、二叉搜索树的概念 二叉搜索树又称为二叉排序树,它或者是一颗空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根结…...

网页html版面分析-- BeauifulSoup(python 文档解析提取)
介绍 BeauifulSoup 是一个可以从HTML或XML 文件中提取数据的python库;它能通过转换器实现惯用的文档导航、查找、修改文档的方式。 BeauifulSoup是一个基于re开发的解析库,可以提供一些强大的解析功能;使用BeauifulSoup 能够提高提取数据的效…...

第五十八节 Java设计模式 - 适配器模式
Java设计模式 - 适配器模式 我们在现实生活中使用适配器很多。例如,我们使用存储卡适配器连接存储卡和计算机,因为计算机仅支持一种类型的存储卡,并且我们的卡与计算机不兼容。 适配器是两个不兼容实体之间的转换器。适配器模式是一种结构模…...

程序员的归宿。。
大家好,我是瑶琴呀。 相信每个进入职场的人都考虑过自己的职业生涯规划,在不同的年龄段可能面临不同挑战,这点对于 35 的人应该更为感同身受。 对于程序员来说,大部分人的职业道路主要是下面三种:第一条,…...
ROS服务器通信
目录 一、角色 二、流程 注意 三、例子描述 四、srv文件 编译配置文件 vscode配置 五、Server.cpp编写例子 编写CMakeList 六、观察server的效果 七、Client编写例子 编写CMakeList 八、观察Client的结果 九、Client优化(动态输入) 了解argc…...

双向带头循环链表(图解)
文章目录 头节点(哨兵位)双向循环结构头插尾插头删尾删在指定位置之前插入数据删除指定位置之前的数据销毁链表 全部代码结语 单链表地址 头节点(哨兵位) 什么是头节点呢?头节点也叫哨兵节点,他在链表中进行不了任何操作,只是用来放哨用的,在单链表中我们当我们尾插的时候我们…...
富文本编辑器 iOS
https://gitee.com/klkxxy/WGEditor-mobile#wgeditor-mobile 采用iOS系统浏览器做的一款富文本编辑器工具。 原理就是使用WKWebView加载一个本地的一个html文件,从而达到编辑器功能的效果! 由于浏览器的一些特性等,富文本编辑器手机端很难做…...

【OceanBase诊断调优】—— checksum error ret=-4103 问题排查
适用版本 OceanBase 数据库所有版本。 什么是 checksum data checksum:一个 SSTable 中所有宏块内存二进制计算出来的 checksum 值。反映了宏块中的数据和数据分布情况。如果宏块中数据一致但是数据分布不一致,计算出来的 checksum 也不相等。 column…...
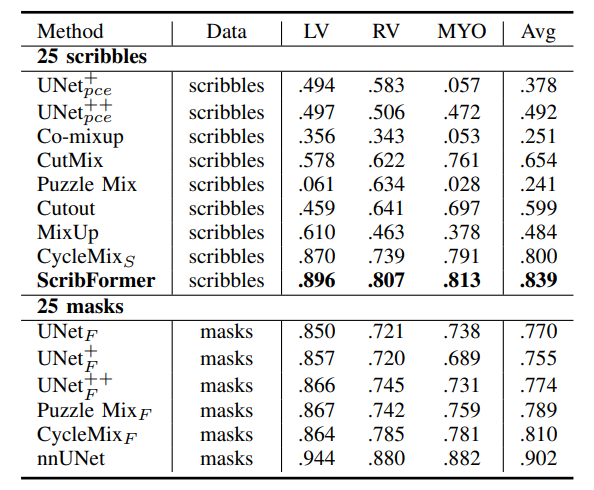
融合Transformer与CNN,实现各任务性能巅峰,可训练参数减少80%
论文er看过来,今天给各位推荐一个热门创新方向:CNNTransformer。 众所周知,CNN通过多层卷积自动学习空间层级特征,能够有效提取图像局部特征。而Transformer通过自注意力机制全局建模,能够有效处理长距离依赖关系。 …...

K8s 多租户管理
一、K8s 多租户管理 多租户是指在同一集群中隔离多个用户或团队,以避免他们之间的资源冲突和误操作。在K8s中,多租户管理的核心目标是在保证安全性的同时,提高资源利用率和运营效率。 在K8s中,该操作可以通过命名空间࿰…...

Java面试题:Synchronized和Lock的对比
Synchronized和Lock对比 语法层面 Synchronized是关键字,源码在jvm中,用c语言实现 使用时,退出同步代码块时会自动释放 Lock是接口,源码由jdk提供,用java语言实现 使用时,需要手动调用unlock方法进行释放 功能层面 都属于悲观锁,具备基本的互斥,同步,锁重入功能 但Lock…...
VPN方案和特点
VPN方案和特点 VPN,或者称为虚拟专用网络,是一种保护你的在线安全和隐私的技术。它可以创建一个加密的连接,使你的在线活动对其他人不可见。以下是一些常见的VPN协议和它们的特点: 开放VPN (OpenVPN):这是一种极为可…...
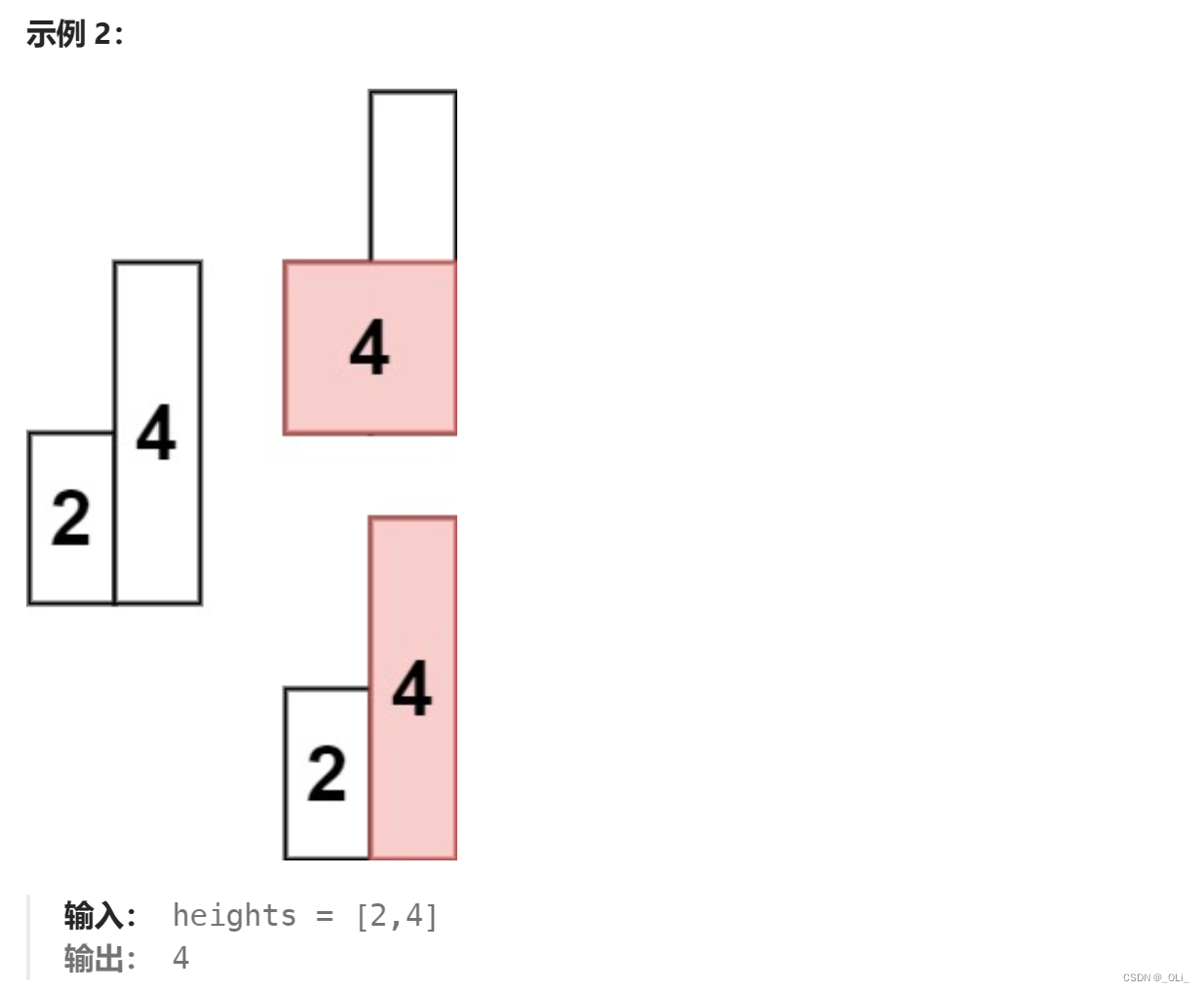
力扣HOT100 - 84. 柱状图中最大的矩形
解题思路: 单调栈 对于一个高度height[ i ],找左右两边均严格小于它的值。 class Solution {public int largestRectangleArea(int[] heights) {int n heights.length;int[] left new int[n];int[] right new int[n];Deque<Integer> mono_st…...
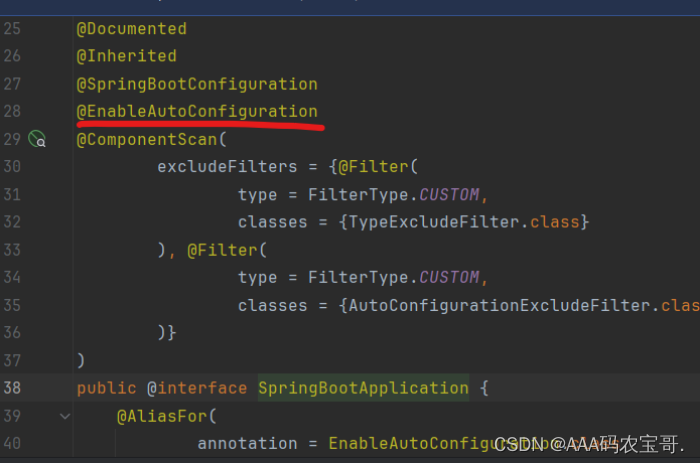
【吃透Java手写】3-SpringBoot-简易版-源码解析
【吃透Java手写】SpringBoot-简易版-源码解析 1 SpringbootDemo2 准备工作2.1 Springboot-my2.1.1 依赖2.1.2 SpringBootApplication2.1.3 SJBSpringApplication2.1.3.1 run方法 2.2 Springboot-user2.2.1 依赖2.2.2 UserController2.2.3 UserApplication 2.3 分析run方法的逻辑…...
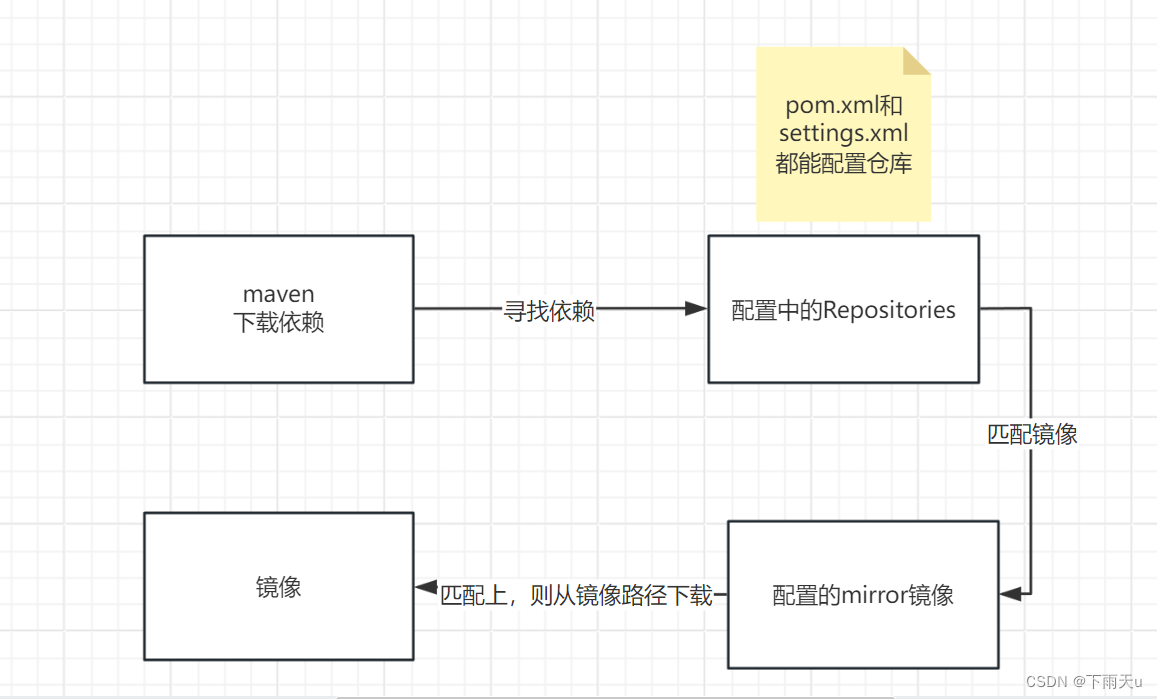
maven mirrorOf的作用
在工作中遇到了一个问题导致依赖下载不了,最后发现是mirror的问题,决定好好去看一下mirror的配置,以及mirrorOf的作用,以前都是直接复制过来使用,看了之后才明白什么意思。 过程 如果你设置了镜像,镜像会匹…...
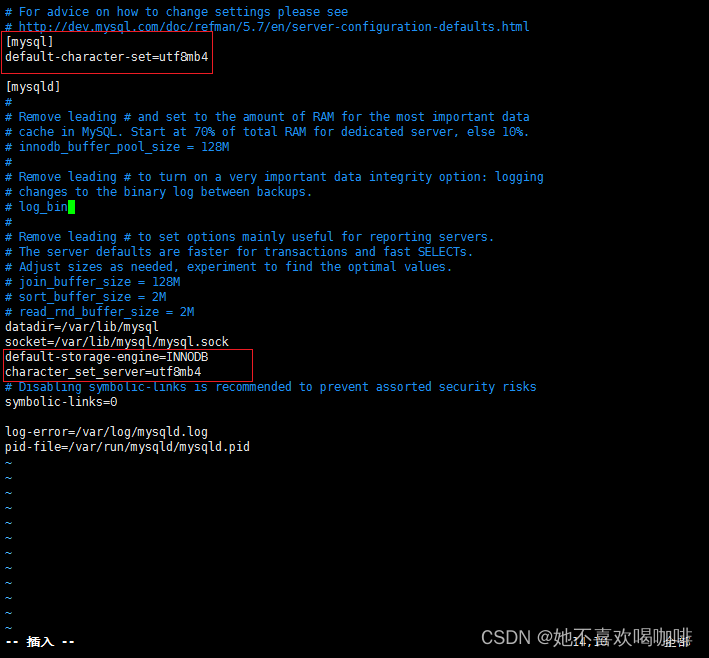
Centos7 安装 MySQL5.7 使用 RPM 方式
1 访问网站 https://downloads.mysql.com/archives/community/ 选择合适的版本,点击 Download。 2 上传下载好的 mysql-5.7.44-1.el7.x86_64.rpm-bundle.tar 文件到 Centos7 机器,这里放到了 下载 目录。 3 解压 mysql-5.7.44-1.el7.x86_64.rpm-bundle.…...

代码随想录算法训练营day21 | 513.找树左下角的值、112. 路径总和、106.从中序与后序遍历序列构造二叉树
513.找树左下角的值 迭代法比较简单,层序遍历,找到最下面一层的第一个节点。题目已经说明节点数>1了 class Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:queue collections.deque()queue.append(root)result ro…...

微信小程序知识点归纳(一)
前言:适用于有一定基础的前端开发同学,完成从网页开发到小程序开发的知识转换。 先立框架,后砌墙壁 回顾:了解微信小程序开发流程-CSDN博客 初始页面结构,三部分pages、utils、配置,分别存放页面、工具类…...
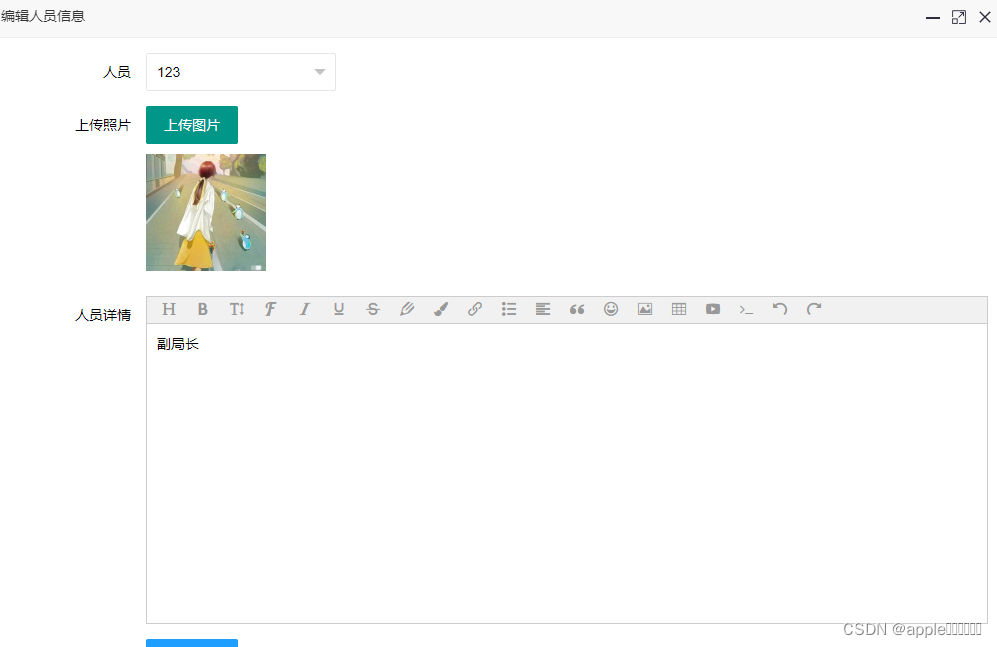
wangEditor富文本编辑器与layui图片上传
记录:js 显示默认的wangEditor富文本编辑器内容和图片 <style>body {background-color: #ffffff;}.layui-form-select dl{z-index:100000;} </style> <div class"layui-form layuimini-form"><div class"layui-form-item"…...

爬虫学习:XPath提取网页数据
目录 一、安装XPath 二、XPath的基础语法 1.选取节点 三、使用XPath匹配数据 1.浏览器审查元素 2.具体实例 四、总结 一、安装XPath 控制台输入指令:pip install lxml 二、XPath的基础语法 XPath是一种在XML文档中查找信息的语言,可以使用它在HTM…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
