判断点在多边形内部
0. 介绍
网上资料很多,只简单介绍下,方便自己今后的理解。
1. 射线法
从该点引一条射线出来,如果和多边形有偶数个交点,则点在多边形外部。
因为有入必有出,所以从外部引进来的射线一定是交多边形偶数个点。
如图

这种方法唯一注意点是处理,引出的这条射线包括了多边形的边或者端点。
对此为了保证不重复,我们忽略在该射线上的边,和终点在该射线上的点。
实现
#define MIN(x,y) (x < y ? x : y)
#define MAX(x,y) (x > y ? x : y)
#define INSIDE 0
#define OUTSIDE 1typedef struct {double x,y;
} Point;int InsidePolygon(Point *polygon,int N,Point p)
{int counter = 0;int i;double xinters;Point p1,p2;p1 = polygon[0];for (i=1;i<=N;i++) {p2 = polygon[i % N];if (p.y > MIN(p1.y,p2.y)) // 确保了点在多边形端点上,点的相邻边只被计算了一次。{if (p.y <= MAX(p1.y,p2.y)) {if (p.x <= MAX(p1.x,p2.x)) {// 为使得水平射线与边相交的条件 // y_0 < y <= y_1// min(x_0,x_1) < xif (p1.y != p2.y) {xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;// 判断点是否在这条边的左侧if (p1.x == p2.x || p.x <= xinters)counter++;}}}}p1 = p2;}if (counter % 2 == 0)return(OUTSIDE);elsereturn(INSIDE);
}
判断点在边的左侧的示意图
2. 内角和
当点在多边形内时,内角和为 2 π 2 \pi 2π。
实现参考
typedef struct {int h,v;
} Point;int InsidePolygon(Point *polygon,int n,Point p)
{int i;double angle=0;Point p1,p2;for (i=0;i<n;i++) {p1.h = polygon[i].h - p.h;p1.v = polygon[i].v - p.v;p2.h = polygon[(i+1)%n].h - p.h;p2.v = polygon[(i+1)%n].v - p.v;angle += Angle2D(p1.h,p1.v,p2.h,p2.v);}if (ABS(angle) < PI)return(FALSE);elsereturn(TRUE);
}/*Return the angle between two vectors on a planeThe angle is from vector 1 to vector 2, positive anticlockwiseThe result is between -pi -> pi
*/
double Angle2D(double x1, double y1, double x2, double y2)
{double dtheta,theta1,theta2;theta1 = atan2(y1,x1);theta2 = atan2(y2,x2);dtheta = theta2 - theta1;while (dtheta > PI)dtheta -= TWOPI;while (dtheta < -PI)dtheta += TWOPI;return(dtheta);
}
3. 同侧法
当多边形为凸多边形时,我们可以判断该点是否在各个边形成的直线的一侧;
来判断点是否在多边形的内部。实际上就是一个线性规划问题。
凹多边形的凹角附近不满足该条件。
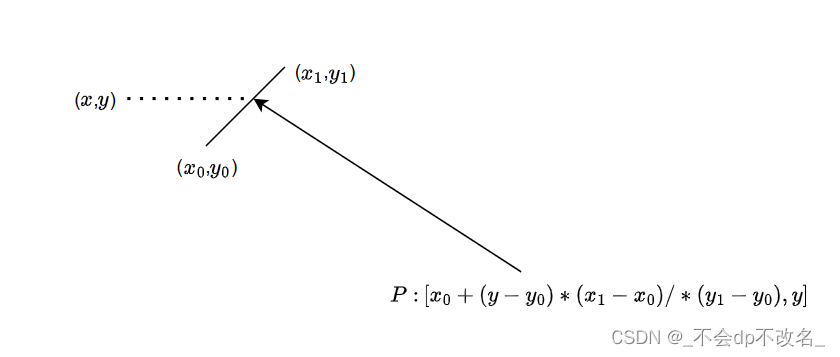
只需要判断
( x − x 0 ) ( y 1 − y 0 ) + ( y − y 0 ) ( x 0 − x 1 ) (x-x_0)(y_1-y_0)+(y-y_0)(x_0-x_1) (x−x0)(y1−y0)+(y−y0)(x0−x1)
的值即可判断,点在多边形边的哪一侧。
给定两个点 P 0 ( x 0 , y 0 ) , P 1 ( x 1 , y 1 ) P_0(x_0,y_0),P_1(x_1,y_1) P0(x0,y0),P1(x1,y1),直线一般方程 A x + B y + c = 0 Ax+By+c=0 Ax+By+c=0推导。
- x 0 = x 1 x_0=x_1 x0=x1
x − x 0 = 0 x-x_0=0 x−x0=0 - x 0 ≠ x 1 x_0 \ne x_1 x0=x1
直线点斜式方程 y = k x + b k = y 1 − y 0 x 1 − x 0 带入 P 0 , P 1 b = y 0 − k x 0 b = y 1 − k x 1 2 b = ( y 0 + y 1 ) − k ( x 0 + x 1 ) 带入 k ,化简得到 b = x 1 y 0 − x 0 y 1 x 1 − x 0 化为一般式子得到 ( y 1 − y 0 ) x + ( x 0 − x 1 ) y + x 1 y 0 − x 0 y 1 = 0 更加统一的形式 ( y 1 − y 0 ) ( x − x 0 ) + x 0 y 1 − x 0 y 0 + ( x 0 − x 1 ) ( y − y 0 ) + x 0 y 0 − x 1 y 0 + x 1 y 0 − x 0 y 1 = 0 合并化简得到 ( x − x 0 ) ( y 1 − y 0 ) − ( y − y 0 ) ( x 1 − x 0 ) = 0 直线点斜式方程y=kx+b\\ k=\frac{y_1- y_0}{x_1-x_0}\\ 带入P_0,P_1\\ b=y_0-kx_0\\ b=y_1-kx_1\\ 2b=(y_0+y_1)-k(x_0+x_1)\\ 带入k,化简得到\\ b=\frac{x_1y_0-x_0y_1}{x_1-x_0}\\ 化为一般式子得到\\ (y_1-y_0)x+(x_0-x_1)y+x_1y_0-x_0y_1=0\\ 更加统一的形式\\(y_1-y_0)(x-x_0)+x_0y_1-x_0y_0+\\(x_0-x_1)(y-y_0)+x_0y_0-x_1y_0+x_1y_0-x_0y_1=0\\ 合并化简得到\\ (x-x_0)(y_1-y_0)-(y-y_0)(x_1-x_0)=0 直线点斜式方程y=kx+bk=x1−x0y1−y0带入P0,P1b=y0−kx0b=y1−kx12b=(y0+y1)−k(x0+x1)带入k,化简得到b=x1−x0x1y0−x0y1化为一般式子得到(y1−y0)x+(x0−x1)y+x1y0−x0y1=0更加统一的形式(y1−y0)(x−x0)+x0y1−x0y0+(x0−x1)(y−y0)+x0y0−x1y0+x1y0−x0y1=0合并化简得到(x−x0)(y1−y0)−(y−y0)(x1−x0)=0 - 将 x 0 = x 1 x_0=x_1 x0=x1代入 ( x − x 0 ) ( y 1 − y 0 ) − ( y − y 0 ) ( x 1 − x 0 ) = 0 (x-x_0)(y_1-y_0)-(y-y_0)(x_1-x_0)=0 (x−x0)(y1−y0)−(y−y0)(x1−x0)=0;
得到 x − x 0 = 0 x-x_0=0 x−x0=0
归纳可得直线一般式方程
( y 1 − y 0 ) x + ( x 0 − x 1 ) y + x 1 y 0 − x 0 y 1 = 0 或 ( x − x 0 ) ( y 1 − y 0 ) − ( y − y 0 ) ( x 1 − x 0 ) = 0 (y_1-y_0)x+(x_0-x_1)y+x_1y_0-x_0y_1=0\\ 或\\ (x-x_0)(y_1-y_0)-(y-y_0)(x_1-x_0)=0 (y1−y0)x+(x0−x1)y+x1y0−x0y1=0或(x−x0)(y1−y0)−(y−y0)(x1−x0)=0
4. 原文
eecs
相关文章:

判断点在多边形内部
0. 介绍 网上资料很多,只简单介绍下,方便自己今后的理解。 1. 射线法 从该点引一条射线出来,如果和多边形有偶数个交点,则点在多边形外部。 因为有入必有出,所以从外部引进来的射线一定是交多边形偶数个点。 如图…...

livox雷达斜装修改
fast_lio中的mid360.yaml中的外参 extrinsic_est_en: false # true: enable the online estimation of IMU-LiDAR extrinsicextrinsic_T: [ -0.011, -0.02329, 0.04412 ]extrinsic_R: [ 1, 0, 0,...
【Spring】初识 Spring AOP(面向切面编程)
目录 1、介绍AOP 1.1、AOP的定义 1.2、AOP的作用 1.3、AOP的核心概念及术语 2、AOP实现示例 3、EnableAspectJAutoProxy注解 1、介绍AOP 1.1、AOP的定义 AOP(Aspect Orient Programming),直译过来就是面向切面编程,AOP 是一…...

k8s各个组件的作用
Kubernetes(K8s)是一个开源的容器编排平台,用于自动化计算机容器化应用程序的部署、扩展和管理。以下是 Kubernetes 中的关键组件及其作用: API 服务器(API Server): 作为集群中所有资源操作的入…...
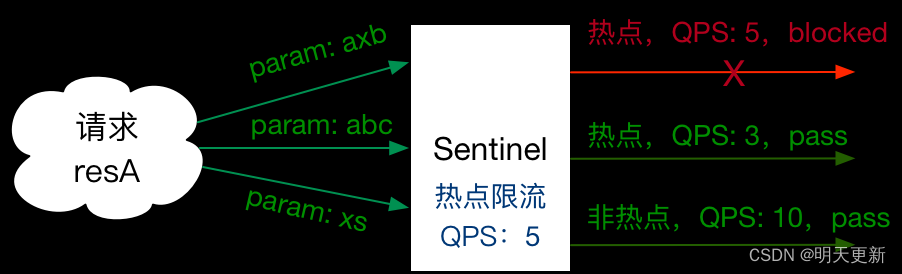
Spring Cloud 整合Sentinel
1、引入依赖 版本说明 alibaba/spring-cloud-alibaba Wiki GitHub 父pom <spring.cloud.version>Hoxton.SR12</spring.cloud.version> <spring.cloud.alibaba.version>2.2.10-RC1</spring.cloud.alibaba.version>Sentinel应用直接引用starter <…...
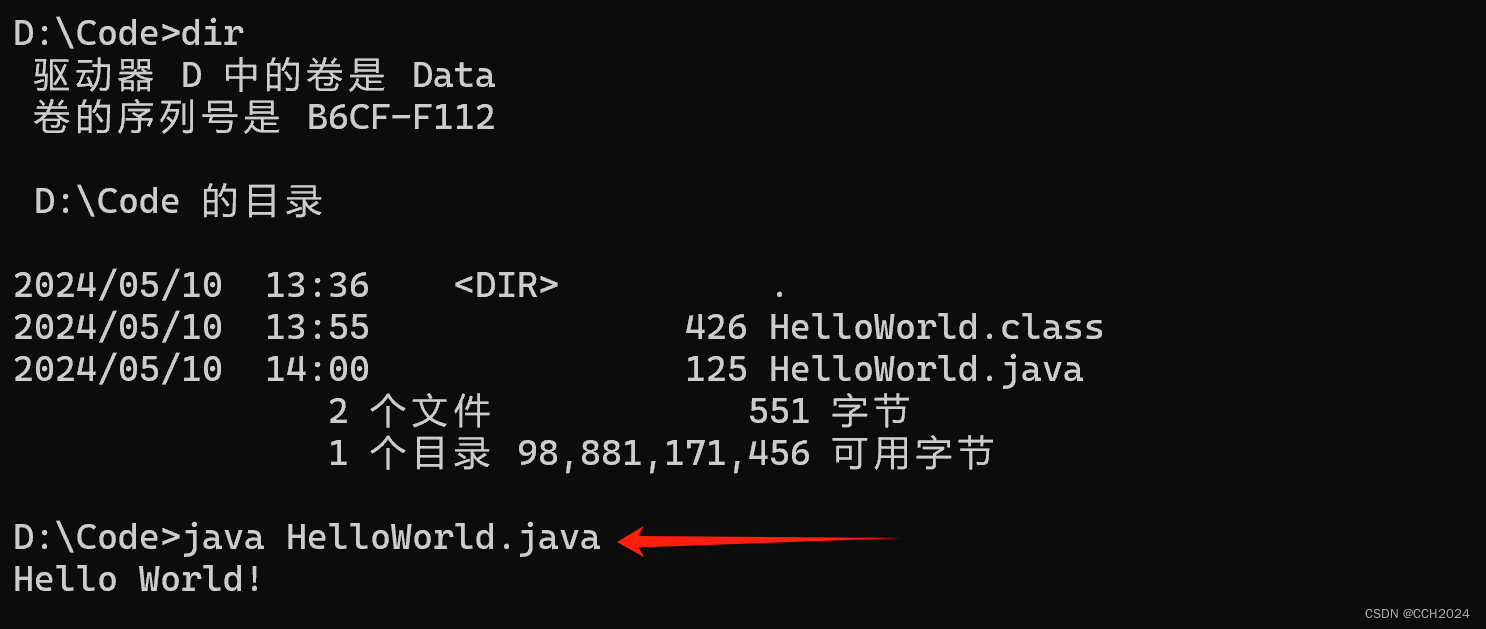
Java入门基础学习笔记4——开发Helloworld入门程序
Java程序开发的三个步骤: 1)编写代码 2)编译代码 3)运行代码 注意事项: 第一个java程序建议使用记事本来编写。 建议代码文件名全英文、首字母大写、满足驼峰模式,源代码文件的后缀必须是.java 注意&a…...

了解WebSocket
1.概念: WebSocket是一种在单个TCP连接上进行全双工通信的协议,属于应用层协议。 WebSocket使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。在WebSocket API中,浏览器和服务器只需要完成一次握…...
从开发角度理解漏洞成因(02)
文章目录 文件上传类需求文件上传漏洞 文件下载类需求文件下载漏洞 扩展 留言板类(XSS漏洞)需求XSS漏洞 登录类需求cookie伪造漏洞万能密码登录 持续更新中… 文章中代码资源已上传资源,如需要打包好的请点击PHP开发漏洞环境(SQL注…...

Web实时通信的学习之旅:轮询、WebSocket、SSE的区别以及优缺点
文章目录 一、通信机制1、轮询1.1、短轮询1.2、长轮询 2、Websocket3、Server-Sent Events 二、区别1、连接方式2、协议3、兼容性4、安全性5、优缺点5.1、WebSocket 的优点:5.2、WebSocket 的缺点:5.3、SSE 的优点:5.4、SSE 的缺点࿱…...
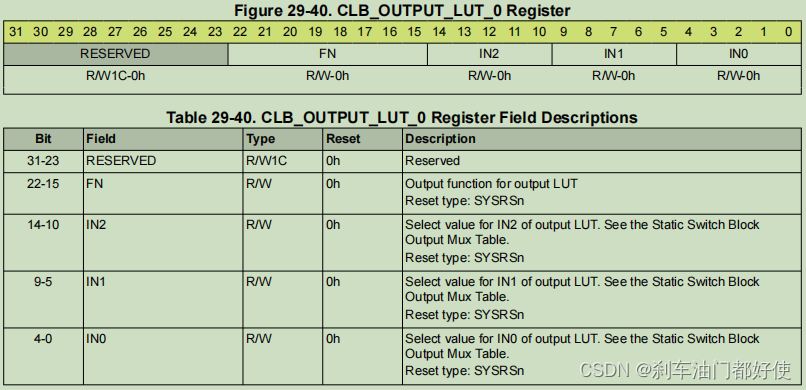
TMS320F280049 CLB模块--LUT4 OUTLUT(4)
LUT4 示意图如下: OUTLUT 示意图如下: 寄存器 参考文档: TMS320F28004x Real-Time Microcontrollers Technical Reference Manual (Rev. G)...
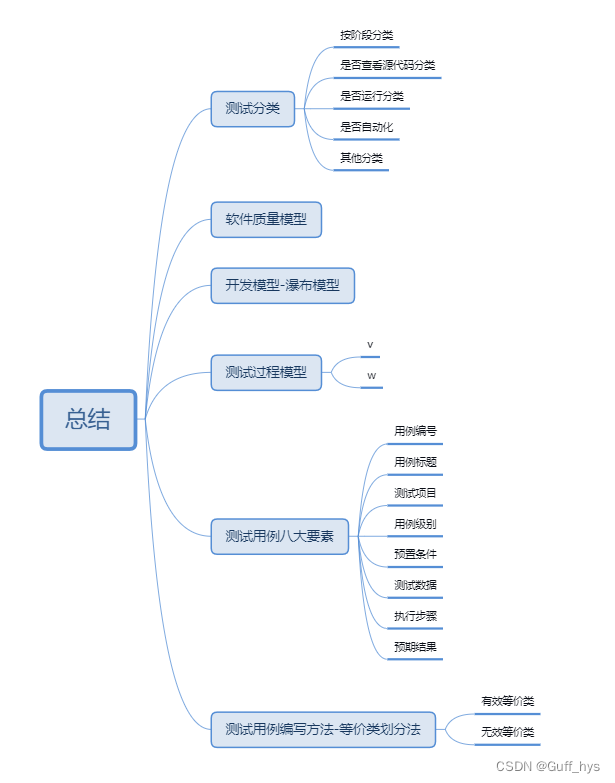
功能测试_分类_用例_方法
总结 测试分类 按阶段分类 是否查看源代码分类 是否运行分类 是否自动化 其他分类 软件质量模型 开发模型-瀑布模型 测试过程模型 v w 测试用例八大要素 用例编号 用例标题 …...

[沫忘录]MySQL 锁
[沫忘录]MySQL 锁 锁能够协调多线程或多进程并发访问某资源产生的数据冲突与错乱。而在数据库中,锁也是协调数据库访问的有效工具。 全局锁 能够锁住当前服务器所有数据库及其表。后续所有事务都只能进行读操作,而不能进行写操作或表属性更改。 典型…...
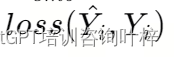
噪声嵌入提升语言模型微调性能
在自然语言处理(NLP)的快速发展中,大模型(LLMs)的微调技术一直是研究的热点。最近,一篇名为《NEFTUNE: NOISY EMBEDDINGS IMPROVE INSTRUCTION FINETUNING》的论文提出了一种新颖的方法,通过在训…...

XML文档基本语法
XML文档基本语法包括以下几个知识点: 开始标记(Start Tag):开始标记是XML元素的起始符号,由左尖括号(<)和元素名称组成。例如,是一个开始标记,表示一个名为"book…...

git开发工作流程
git开发工作流程 (1)先将远程代码pull到本地 (2)在本地上分支上进行开发 (3)开发完之后,push到远程分支 (4)由远程的master进行所有分支合并...

JDK生成https配置
keytool -genkey -v -alias tomcat -keyalg RSA -keystore D:\https证书\weChat.keystore -validity 36500 -keypass 250250 keytool -importkeystore -srcstoretype JKS -srckeystore D:\https证书\weChat.keystore -srcstorepass 250250 -srcalias tomcat -srckeypass 25025…...
通过 Java 操作 redis -- set 集合基本命令
目录 使用命令 sadd ,smembers 使用命令 sismember 使用命令 scard 使用命令 spop 使用命令 sinter,sinterstore,sunion,sunionstore,sdiff,sdiffstore 关于 redis set 集合类型的相关命令推荐看Redis …...
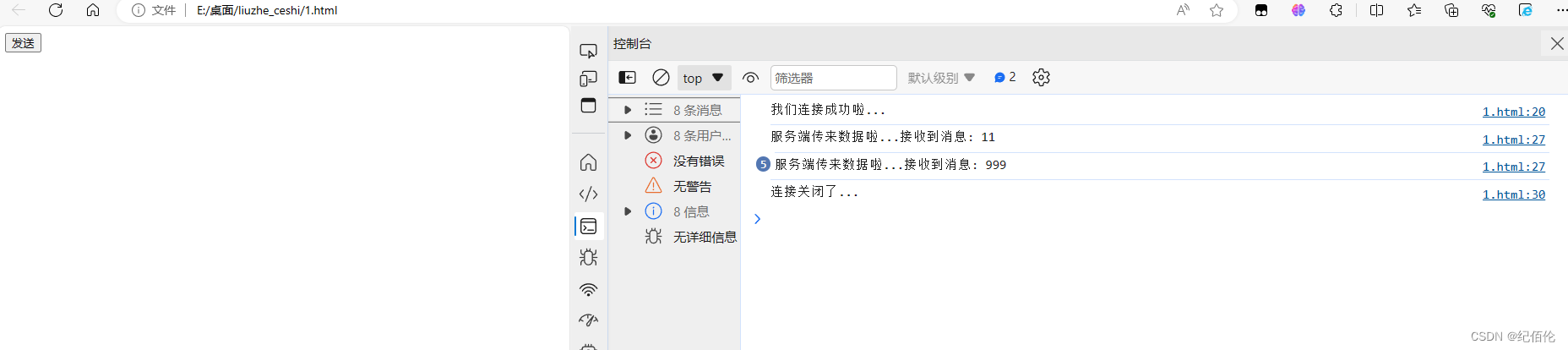
WebSocket前后端建立以及使用
1、什么是WebSocket WebSocket 是一种在 Web 应用程序中实现双向通信的协议。它提供了一种持久化的连接,允许服务器主动向客户端推送数据,同时也允许客户端向服务器发送数据,实现了实时的双向通信。 这部分直接说你可能听不懂;我…...
C++数据结构之链表树图的存储
本文主要介绍用数组存储,结构只做简单介绍 目录 文章目录 前言 结构体实现 1、链表的存储 2、树的存储 3、图的存储 数组实现 1、链表实现 2、树和图的实现 总结 前言 在正常工程中,我们通常使用结构体或者类,来定义并使用如链表…...
又一位互联网大佬转行当网红,能写进简历么?
最近半个月,有两个中年男人仿佛住进了热搜。 一个是刚刚辟谣自己“卡里没有冰冷的 40 亿”的雷军,另一个则是在今年年初就高呼“如果有可能,企业家都要去当网红”的 360 创始人周鸿祎。 他也确实做到了。 先是作为当年 3Q 大战的当事人&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
