洛谷 P3391:文艺平衡树 ← Splay树模板题
【题目来源】
https://www.luogu.com.cn/problem/P3391
【题目描述】
您需要写一种数据结构(可参考题目标题),来维护一个有序数列。 其中需要提供以下操作:翻转一个区间,例如原有序序列是 5 4 3 2 1,翻转区间是 [2,4] 的话,结果是 5 2 3 4 1。
【输入格式】
第一行两个正整数 n,m,表示序列长度与操作个数。序列中第 i 项初始为 i。 接下来 m 行,每行两个正整数 l,r,表示翻转的区间。 输出格式 输出一行 n 个正整数,表示原始序列经过 m 次变换后的结果。
【输出格式】
输出一行 n 个正整数,表示原始序列经过 m 次变换后的结果。
【输入样例】
5 3
1 3
1 3
1 4
【输出样例】
4 3 2 1 5
【数据范围】
对于 100% 的数据,1≤n,m≤100000,1≤l≤r≤n。
【算法分析】
Splay 树简介:https://blog.csdn.net/hnjzsyjyj/article/details/138504578
● Treap 树解决平衡的办法是给每个结点加上一个随机的优先级,实现概率上的平衡。Splay 树直接用旋转调整树的形态,通过旋转改善树的平衡性。计算量小,效果好。
● Splay 树的旋转主要分为“单旋”和“双旋”。
所谓“单旋”,即把结点 x 与它的父结点交换位置,使结点 x 上升一层。“单旋”不会减少树的层数,对改善平衡性没有帮助。根据旋转方向,“单旋”又分为左旋(zag)与右旋(zig)。
所谓“双旋”,即两次“单旋”。“双旋”同时旋转结点 x,父结点 f 及祖父结点 g 等3个结点,能改善平衡性。“双旋”又分为“一字旋”与“之字旋”。
● Splay 树的旋转示意图
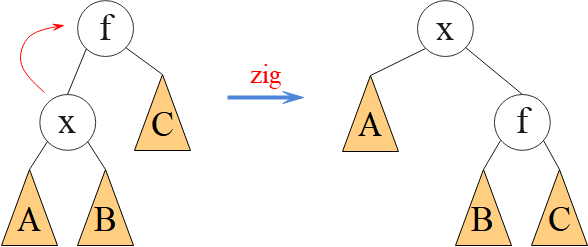

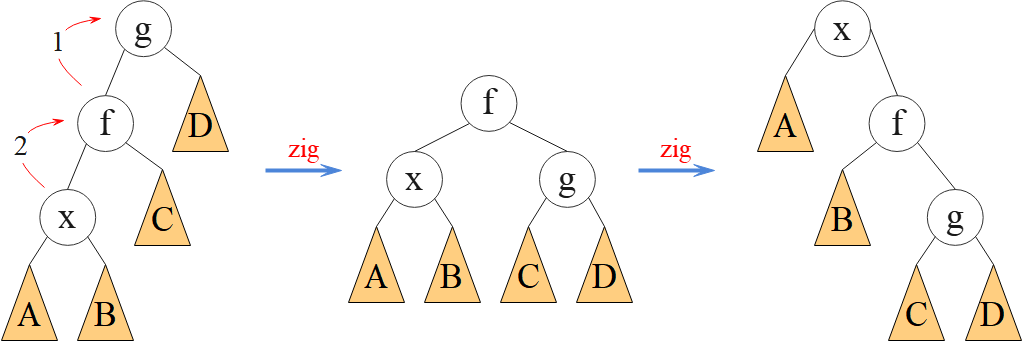
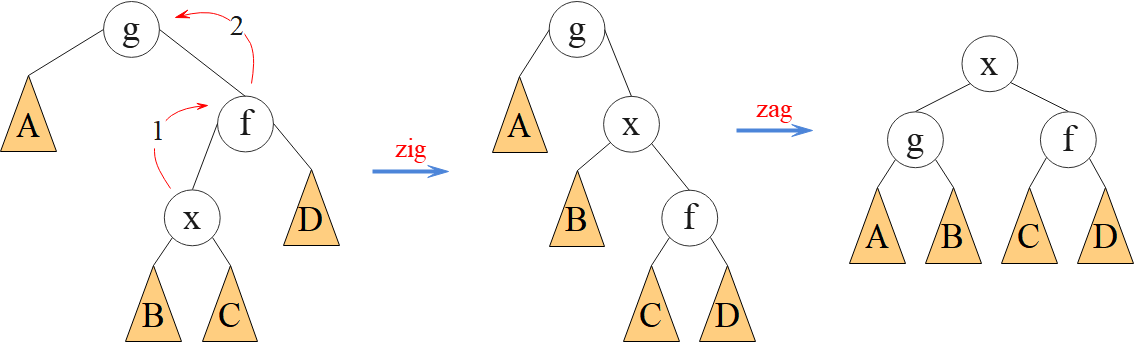
● Splay 树的基本操作是把结点旋转到树的根部,这样下次访问它时,只需查一次就 OK 了。
● Splay 树是动态树(LCT,Link Cut Tree)与树链剖分的基础。
● Splay 树曾经是最常使用的 BST。不过,现在经常使用 FHQ Treap 树实现很多传统的 Splay 树的题目。因为,FHQ Treap 树代码更容易写,效率也很高,且可做持久化。
【算法代码】
下面代码是 Splay 树的模板代码,但其中包含了本题(洛谷 P3391)未用的函数。例如:
本例使用了 pushup()、pushdown()、rotate()、splay()、insert()、get_val_by_pri() 、output() 等7个函数;未使用 find()、get_pre()、get_suc()、remove()、get_pri_by_val() 等5个函数。
#include <bits/stdc++.h>
using namespace std;const int maxn=1e5+5;
int n,m;
int root,idx;struct Node {int s[2],v,p; //subtree,val,rootint size,cnt;int lazy;
} tr[maxn];void pushup(int x) {tr[x].size=tr[tr[x].s[0]].size+tr[tr[x].s[1]].size+tr[x].cnt;
}void pushdown(int x) {if(tr[x].lazy) {swap(tr[x].s[0],tr[x].s[1]);tr[tr[x].s[0]].lazy^=1;tr[tr[x].s[1]].lazy^=1;tr[x].lazy=0;}
}void rotate(int x) {int y=tr[x].p;int z=tr[y].p;int k=(tr[y].s[1]==x);tr[z].s[tr[z].s[1]==y]=x, tr[x].p=z;tr[y].s[k]=tr[x].s[k^1], tr[tr[x].s[k^1]].p=y;tr[x].s[k^1]=y, tr[y].p=x;pushup(y), pushup(x);
}void splay(int x,int k) {while(tr[x].p!=k) {int y=tr[x].p;int z=tr[y].p;if(z!=k) {if((tr[y].s[0]==x)^(tr[z].s[0]==y)) rotate(x);else rotate(y);}rotate(x);}if(!k) root=x;
}void insert(int x) {int u=root, p=0;while(u && tr[u].v!=x) {p=u;u=tr[u].s[x>tr[u].v];}if(u) tr[u].cnt++;else {u=++idx;if(p) tr[p].s[x>tr[p].v]=u;tr[u].p=p, tr[u].v=x, tr[u].size=1;tr[u].cnt=1;}splay(u,0);
}void find(int x) {int u=root;while(tr[u].s[x>tr[u].v] && tr[u].v!=x) u=tr[u].s[x>tr[u].v];splay(u,0);
}int get_pre(int x) {find(x);if(tr[root].v<x) return root;int u=tr[root].s[0];while(tr[u].s[1]) u=tr[u].s[1];splay(u,0);return u;
}int get_suc(int x) {find(x);if(tr[root].v>x) return root;int u=tr[root].s[1];while(tr[u].s[0]) u=tr[u].s[0];splay(u,0);return u;
}void remove(int x) {int pre=get_pre(x), suc=get_suc(x);splay(pre,0), splay(suc,pre);int del=tr[suc].s[0];if(tr[del].cnt>1) tr[del].cnt--, splay(del,0);else tr[suc].s[0]=0, splay(suc,0);
}int get_pri_by_val(int x) {insert(x);int ans=tr[tr[root].s[0]].size;remove(x);return ans;
}int get_val_by_pri(int x) {int u=root;while(true) {pushdown(u);if(x<=tr[tr[u].s[0]].size) u=tr[u].s[0];else if(x==tr[tr[u].s[0]].size+1) return u;else x-=tr[tr[u].s[0]].size+1, u=tr[u].s[1];}return -1;
}void output(int x) {pushdown(x);if(tr[x].s[0]) output(tr[x].s[0]);if(1<=tr[x].v && tr[x].v<=n) printf("%d ",tr[x].v);if(tr[x].s[1]) output(tr[x].s[1]);
}int main() {scanf("%d %d",&n,&m);for(int i=0; i<=n+1; i++) insert(i);while(m--) {int le,ri;scanf("%d%d",&le,&ri);le=get_val_by_pri(le);ri=get_val_by_pri(ri+2);splay(le,0);splay(ri,le);tr[tr[ri].s[0]].lazy^=1;}output(root); //inorderreturn 0;
}/*
in:
5 3
1 3
1 3
1 4out:
4 3 2 1 5
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/138504578
https://www.acwing.com/file_system/file/content/whole/index/content/6921304/
https://www.acwing.com/file_system/file/content/whole/index/content/6420964/
相关文章:

洛谷 P3391:文艺平衡树 ← Splay树模板题
【题目来源】https://www.luogu.com.cn/problem/P3391【题目描述】 您需要写一种数据结构(可参考题目标题),来维护一个有序数列。 其中需要提供以下操作:翻转一个区间,例如原有序序列是 5 4 3 2 1,翻转区间…...

【高校科研前沿】北师大陈晋教授团队在遥感顶刊发表最新成果:ClearSCD模型:在高空间分辨率遥感影像中综合利用语义和变化关系进行语义变化检测
01文章简介 论文名称:The ClearSCD model: Comprehensively leveraging semantics and change relationships for semantic change detection in high spatial resolution remote sensing imagery(ClearSCD模型:在高空间分辨率遥感影像中综合…...

关于YOLO8学习(五)安卓部署ncnn模型--视频检测
教学视频地址 B站 前文 关于YOLO8学习(一)环境搭建,官方检测模型部署到手机 关于YOLO8学习(二)数据集收集,处理 关于YOLO8学习(三)训练自定义的数据集 关于YOLO8学习(四)模型转换为ncnn 简介 本文将会讲解: (1)使用前文生成的ncnn模型,部署到安卓端,并且实…...

从哪些方面可以看出光伏的未来发展好?
光伏发电是一种基于半导体材料的光伏效应将太阳光转化为直流电能的发电技术。近年来,随着全球对可再生能源和环境保护的关注度不断提升,光伏发电行业发展迅速,成为未来能源领域的重要发展方向。 首先,从能源角度来看,光…...

VBA_MF系列技术资料1-605
MF系列VBA技术资料1-605 为了让广大学员在VBA编程中有切实可行的思路及有效的提高自己的编程技巧,我参考大量的资料,并结合自己的经验总结了这份MF系列VBA技术综合资料,而且开放源码(MF04除外),其中MF01-0…...

算法题① —— 数组专栏
1. 滑动窗口 1.1 长度最小的子数组 力扣:https://leetcode.cn/problems/minimum-size-subarray-sum/description/ int minSubArrayLen(int s, vector<int>& nums) {int result INT32_MAX; int sum 0; // 子序列的数值之和int subLength 0; // 子序列…...
)
算法学习笔记(差分约束系统)
前置:spfa 从例题入手: 【模板】差分约束系统 | StarryCoding 题目描述 给定 n n n未知量和一个大小为 m m m的不等式(或等式)组,请你判断这个不等式(或等式)组是否有解。 1 1 1 i i i j …...

HCIP的学习(14)
过滤策略—filter-policy 思科中:分发列表 过滤策略是只能够针对于路由信息进行筛选(过滤)的工具,而无法针对于LSA进行过滤。 在R4的出方向上配置过滤策略,使得R1不能学习到23.0.0.0/24路由信息1、抓取流量 […...

行业新应用:电机驱动将成为机器人的动力核心
电机已经遍布当今社会人们生活的方方面面,不仅应用范围越来越广,更新换代的速度也日益加快。按照工作电源分类,可以将它划分为直流电机和交流电机两大类型。直流电机中,按照线圈类型分类,又可以分为有铁芯的电机、空心…...

大模型模型简化机器人训练;简单易用的 3D 工具Project Neo;特斯拉放出了擎天柱机器人最新训练视频
✨ 1: DrEureka 利用大语言模型自动化将机器人仿真环境训练结果转移到真实世界 DrEureka是一种利用大型语言模型(LLMs)自动化和加速从仿真(sim)到现实世界(real)转移的技术。在机器人技能学习领域&#x…...
Win11安装Docker Desktop运行Oracle 11g 【详细版】
oracle docker版本安装教程 步骤拉取镜像运行镜像进入数据库配置连接数据库,修改密码Navicat连接数据库 步骤 拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/helowin/oracle_11g运行镜像 docker run -d -p 1521:1521 --name oracle11g registry.cn-ha…...
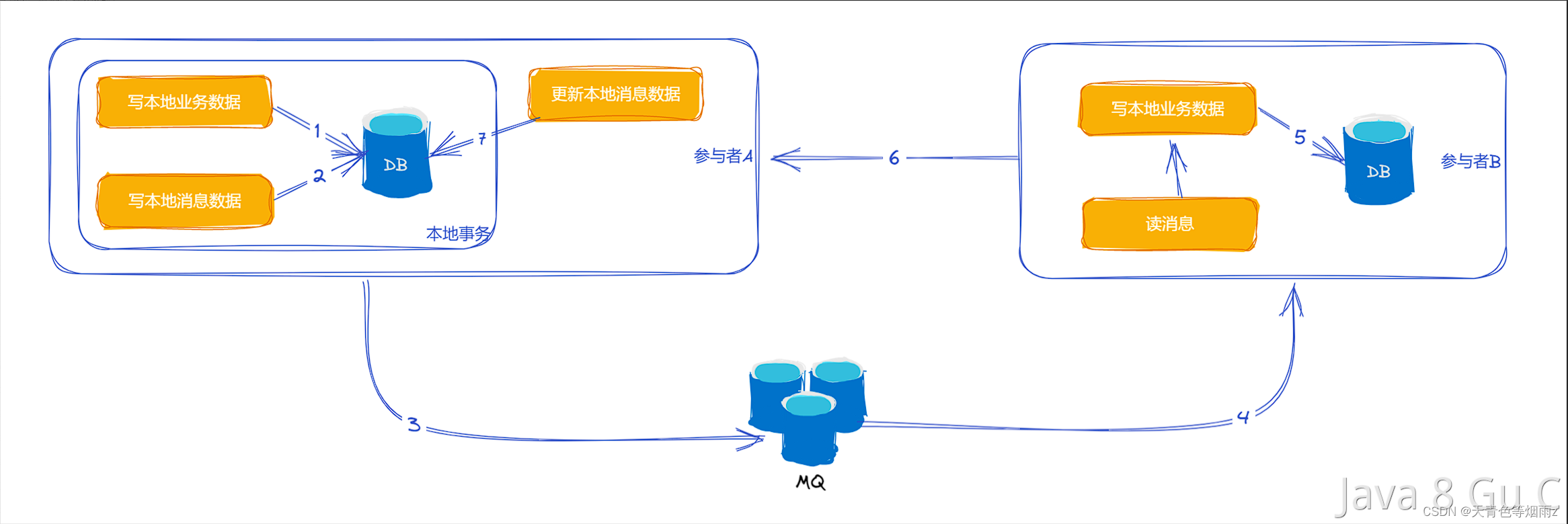
分布式事务?哪几种方式实现?一文看懂!
什么是分布式事务 分布式事务是指在分布式系统中涉及到多个数据库或多个应用程序之间的事务处理,这些数据库或应用程序可能分布在不同的物理节点上,甚至可能位于不同的地理位置。在分布式事务中,需要确保所有参与者的事务操作都能够保持一致性…...
词令蚂蚁庄园今日答案如何在微信小程序查看蚂蚁庄园今天问题的正确答案?
词令蚂蚁庄园今日答案如何在微信小程序查看蚂蚁庄园今天问题的正确答案? 1、打开微信,点击搜索框; 2、打开搜索页面,选择小程序搜索; 3、在搜索框,输入词令搜索点击进入词令微信小程序; 4、打开…...

【Delphi 爬虫库 6】使用正则表达式提取猫眼电影排行榜top100
正则表达式库的简单介绍 正则表达式易于使用,功能强大,可用于复杂的搜索和替换以及基于模板的文本检查。这对于输入形式的用户输入验证特别有用-验证电子邮件地址等。您还可以从网页或文档中提取电话号码,邮政编码等,在日志文件中…...

Markdown和Latex中文字上下标的方法
技术背景 在Markdown和Latex中,如果只是写公式,不论是行内公式还是行间公式,都可以直接使用^和_这两个符号实现上下标。但有个问题是,如果只是使用公式来做上下标,出来的字体是斜着的。例如这样的语法: $$ …...
VSCode:设置顶部文件标签页滚动条的宽度
使用VSCode打开多个文件后,顶部的文件标签可以通过滚动条进行滚动,但是缺点是该滚动条太窄了,不好选择。 可以通过如下方法修改改滚动条的宽度: 1.点击设置 2.选择工作台->编辑管理->Title Scrollbar Sizing->Large 3.可…...

MySQL变量的定义与使用
# 关系运算 select x < y as 大小判断;# 返回结果1代表true,如果是0代表false select x > y; # 逻辑运算 select TRUE and FALSE;# 依然符合&(and)与、|(or)或、^(xor)亦或。 select …...

python-pytorch seq2seq+attention笔记0.5.00
python-pytorch seq2seq+attention笔记0.5.00 1. LSTM模型的数据size2. 关于LSTM的输入数据包含hn和cn时,hn和cn的size3. LSTM参数中默认batch_first4. Attention机制的三种算法5. 模型的编码器6. 模型的解码器7. 最终模型8. 数据的准备9. 遇到的问题10. 完整代码1. LSTM模型的…...

ansible 深入介绍之 主机清单与playbook
目录 一 inventory 主机清单 1,主机清单 是什么 2,主机清单 定义方式 2.1 自定义主机端口 2.2 定义 范围ip 地址 2.3 定义 拥有相似的主机名 3, inventory 中的变量 3.1 常见 变量 3.2 主机变量 3.3 组变量 3.…...

【MySQ】9.构建高可用数据库:MySQL集群模式部署大全
单个MySQL节点的主要风险在于它构成了一个单点故障,这意味着任何硬件故障、软件崩溃或维护需求都可能导致整个数据库服务中断,从而影响到业务的连续性和数据的安全性。此外,它还限制了系统的扩展性,使得性能提升和负载均衡变得困难…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
