【贪心算法】哈夫曼编码Python实现
文章目录
- @[toc]
- 哈夫曼编码
- 不同编码方式对比
- 前缀码
- 构造哈夫曼编码
- 哈夫曼算法的正确性
- 贪心选择性质
- 证明
- 最优子结构性质
- 证明
- 总结
- `Python`实现
- 时间复杂性
文章目录
- @[toc]
- 哈夫曼编码
- 不同编码方式对比
- 前缀码
- 构造哈夫曼编码
- 哈夫曼算法的正确性
- 贪心选择性质
- 证明
- 最优子结构性质
- 证明
- 总结
- `Python`实现
- 时间复杂性
哈夫曼编码
- 哈夫曼编码是广泛用于数据文件压缩的十分有效的编码方法,其压缩率通常为 20 % 20\% 20%到 90 % 90\% 90%
- 哈夫曼编码算法使用字符在文件中出现的频率表来建立一个用 0 0 0、 1 1 1串表示各字符的最优表示方式
不同编码方式对比
- 假设有一个数据文件包含 100000 100000 100000个字符,要用压缩的方式存储它,该文件中共有 6 6 6个不同字符出现,各字符出现的频率如下表所示
| a a a | b b b | c c c | d d d | e e e | f f f | |
|---|---|---|---|---|---|---|
| 频率(千次) | 45 45 45 | 13 13 13 | 12 12 12 | 16 16 16 | 9 9 9 | 5 5 5 |
- 有多种方法表示文件中的信息,考察用 0 0 0、 1 1 1码串表示字符的方法,即每个字符用唯一的一个 0 0 0、 1 1 1串表示
- 若使用定长码,则表示 6 6 6个不同的字符需要 3 3 3位: a = 000 a = 000 a=000, b = 001 b = 001 b=001, ⋯ \cdots ⋯, f = 101 f = 101 f=101,用这种方法对整个文件进行编码需要 300000 300000 300000位
- 使用变长码要比使用定长码好得多,给出现频率高的字符较短的编码,出现频率较低的字符以较长的编码,可以大大缩短总码长,下表给出了一种变长码编码方案,其中 a a a用一位串 0 0 0表示,而字符 f f f用 4 4 4位串 1100 1100 1100表示
| a a a | b b b | c c c | d d d | e e e | f f f | |
|---|---|---|---|---|---|---|
| 变长码 | 0 0 0 | 101 101 101 | 100 100 100 | 111 111 111 | 1101 1101 1101 | 1100 1100 1100 |
- 用这种编码方案,整个文件的总码长为 ( 45 × 1 + 13 × 3 + 12 × 3 + 16 × 3 + 9 × 4 + 5 × 4 ) × 1000 = 224000 (45 \times 1 + 13 \times 3 + 12 \times 3 + 16 \times 3 + 9 \times 4 + 5 \times 4) \times 1000 = 224000 (45×1+13×3+12×3+16×3+9×4+5×4)×1000=224000位,比用定长码方案好,总码长减小约 25 % 25\% 25%,事实上,这是该文件的最优编码方案
前缀码
- 对每一个字符规定一个 0 0 0、 1 1 1串作为其代码,并要求任一字符的代码都不是其他字符代码的前缀,这种编码称为前缀码
- 编码的前缀性质可以使译码方法非常简单,由于任一字符的代码都不是其他字符代码的前缀,从编码文件中不断取出代表某一字符的前缀码,转换为原始字符串,即可逐个译出文件中的所有字符
- 例如上表中的变长码就是一种前缀码,对于给定的 0 0 0、 1 1 1串 001011101 001011101 001011101可以唯一地分解为 0 0 0、 0 0 0、 101 101 101、 1101 1101 1101,因而其译码为 a a b e aabe aabe
- 译码过程需要方便地取出编码的前缀,因此需要表示前缀码的合适的数据结构,为此可以用二叉树作为前缀编码的数据结构
- 在表示前缀码的二叉树中,树叶代表给定的字符,并将每个字符的前缀码看作从树根到代表该字符的树叶的一条路径
- 定长编码的二叉树表示

- 最优前缀编码的二叉树表示

- 最优前缀码的二叉树总是一棵完全二叉树,即树中任意结点都有 2 2 2个儿子,在一般情况下,若 C C C是字符集,表示其最优前缀码的二叉树中恰有 ∣ C ∣ |C| ∣C∣个叶子,每个叶子对应字符集中的一个字符,该二叉树恰有 ∣ C ∣ − 1 |C| - 1 ∣C∣−1个内部结点
- 给定编码字符集 C C C及其频率分布 f f f,即 C C C中任一字符 c c c以频率 f ( c ) f(c) f(c)在数据文件中出现, C C C的一个前缀码编码方案对应一棵二叉树 T T T,字符 c c c在树中的深度记为 d T ( c ) d_{T}(c) dT(c), d T ( c ) d_{T}{(c)} dT(c)也是字符 c c c的前缀码长,该编码方案的平均码长定义为 B ( T ) = ∑ c ∈ C f ( c ) d T ( c ) B(T) = \displaystyle\sum\limits_{c \in C}{f(c) d_{T}(c)} B(T)=c∈C∑f(c)dT(c),使平均码长达到最小的前缀码编码方案称为 C C C的最优前缀码
构造哈夫曼编码
-
哈夫曼提出了构造最优前缀码的贪心算法,由此产生的编码方案称为哈夫曼算法
-
哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树 T T T
-
算法以 ∣ C ∣ |C| ∣C∣个叶节点开始,执行 ∣ C ∣ − 1 |C| - 1 ∣C∣−1次的“合并”运算后产生最终要求的树 T T T
-
首先用字符集 C C C中每个字符 c c c的频率 f ( c ) f(c) f(c)初始化优先队列 Q Q Q,然后不断地从优先队列 Q Q Q中取出具有最小频率的两棵树 x x x和 y y y( f ( x ) ≤ f ( y ) f(x) \leq f(y) f(x)≤f(y)),将它们合并为一棵新树 z z z, z z z的频率是 x x x和 y y y的频率之和,新树 z z z以 x x x为其左儿子,以 y y y为其右儿子,经过 n − 1 n - 1 n−1次的合并后,优先队列中只剩下一棵树,即所要求的树 T T T
哈夫曼算法的正确性
- 要证明哈夫曼算法的正确性,只要证明最优前缀码问题具有贪心选择性质和最优子结构性质
贪心选择性质
- 设 C C C是编码字符集, C C C中字符 c c c的频率为 f ( c ) f(c) f(c),又设 x x x和 y y y是 C C C中具有最小频率的两个字符,则存在 C C C的最优前缀码使 x x x和 y y y具有相同码长且仅最后一位编码不同
证明
- 设二叉树 T T T表示 C C C的任意一个最优前缀码,下面证明可以对 T T T进行适当修改后,得到一棵新的二叉树 T ′ ′ T^{''} T′′,使得在新树中, x x x和 y y y是最深叶子且为兄弟,同时新树 T ′ ′ T^{''} T′′表示的前缀码也是 C C C的最优前缀码,如果能做到,则 x x x和 y y y在 T ′ ′ T^{''} T′′表示的最优前缀码中就具有相同的码长且仅最后一位编码不同
- 设 b b b和 c c c是二叉树 T T T的最深叶子且为兄弟,不失一般性,可设 f ( b ) ≤ f ( c ) f(b) \leq f(c) f(b)≤f(c), f ( x ) ≤ f ( y ) f(x) \leq f(y) f(x)≤f(y),由于 x x x和 y y y是 C C C中具有最小频率的两个字符,故 f ( x ) ≤ f ( b ) f(x) \leq f(b) f(x)≤f(b), f ( y ) ≤ f ( c ) f(y) \leq f(c) f(y)≤f(c)
- 首先在树 T T T中交换叶子 b b b和 x x x的位置得到树 T ′ T^{'} T′,然后在树 T ′ T^{'} T′中再交换叶子 c c c和 y y y的位置,得到树 T ′ ′ T^{''} T′′,如下图所示

- 由此可知,树 T T T和 T ′ T^{'} T′表示的前缀码的平均码长之差为
B ( T ) − B ( T ′ ) = ∑ c ∈ C f ( c ) d T ( c ) − ∑ c ∈ C f ( c ) d T ′ ( c ) = f ( x ) d T ( x ) + f ( b ) d T ( b ) − f ( x ) d T ′ ( x ) − f ( b ) d T ′ ( b ) = f ( x ) d T ( x ) + f ( b ) d T ( b ) − f ( x ) d T ( b ) − f ( b ) d T ( x ) = ( f ( b ) − f ( x ) ) ( d T ( b ) − d T ( x ) ) ≥ 0 \begin{aligned} B(T) - B(T^{'}) &= \displaystyle\sum\limits_{c \in C}{f(c) d_{T}(c)} - \displaystyle\sum\limits_{c \in C}{f(c) d_{T^{'}}(c)} \\ &= f(x) d_{T}{(x)} + f(b) d_{T}{(b)} - f(x) d_{T^{'}}(x) - f(b) d_{T^{'}}(b) \\ &= f(x) d_{T}{(x)} + f(b) d_{T}{(b)} - f(x) d_{T}(b) - f(b) d_{T}(x) \\ &= (f(b) - f(x))(d_{T}(b) - d_{T}(x)) \geq 0 \end{aligned} B(T)−B(T′)=c∈C∑f(c)dT(c)−c∈C∑f(c)dT′(c)=f(x)dT(x)+f(b)dT(b)−f(x)dT′(x)−f(b)dT′(b)=f(x)dT(x)+f(b)dT(b)−f(x)dT(b)−f(b)dT(x)=(f(b)−f(x))(dT(b)−dT(x))≥0
- 类似地,可以证明在 T ′ T^{'} T′中交换 y y y与 c c c的位置也不增加平均码长,即 B ( T ′ ) − B ( T ′ ′ ) B(T^{'}) - B(T^{''}) B(T′)−B(T′′)也是非负的
- 由此可知, B ( T ′ ′ ) ≤ B ( T ′ ) ≤ B ( T ) B(T^{''}) \leq B(T^{'}) \leq B(T) B(T′′)≤B(T′)≤B(T),另一方面, T T T表示的前缀码是最优的,故 B ( T ) ≤ B ( T ′ ′ ) B(T) \leq B(T^{''}) B(T)≤B(T′′),因此 B ( T ) = B ( T ′ ′ ) B(T) = B(T^{''}) B(T)=B(T′′),即 T ′ ′ T^{''} T′′表示的前缀码也是最优前缀码,且 x x x和 y y y具有最长的码长,同时仅最后一位编码不同
最优子结构性质
- 设 T T T是表示字符集 C C C的一个最优前缀码的完全二叉树, C C C中字符 c c c的出现频率为 f ( c ) f(c) f(c),设 x x x和 y y y是树 T T T中的两个叶子且为兄弟, z z z是它们的父亲,若将 z z z看作具有频率 f ( z ) = f ( x ) + f ( y ) f(z) = f(x) + f(y) f(z)=f(x)+f(y)的字符,则树 T ′ = T − { x , y } T^{'} = T - \set{x , y} T′=T−{x,y}表示字符集 C ′ = ( C − { x , y } ) ∪ { z } C^{'} = (C - \set{x , y}) \cup \set{z} C′=(C−{x,y})∪{z}的一个最优前缀码
证明
- 首先证明 T T T的平均码长 B ( T ) B(T) B(T)可用 T ′ T^{'} T′的平均码长 B ( T ′ ) B(T^{'}) B(T′)来表示
- 事实上,对任意 c ∈ C − { x , y } c \in C - \set{x , y} c∈C−{x,y}有 d T ( c ) = d T ′ ( c ) d_{T}(c) = d_{T^{'}}(c) dT(c)=dT′(c),故 f ( c ) d T ( c ) = f ( c ) d T ′ ( c ) f(c) d_{T}(c) = f(c) d_{T^{'}}(c) f(c)dT(c)=f(c)dT′(c)
- 另一方面, d T ( x ) = d T ( y ) = d T ′ ( z ) + 1 d_{T}(x) = d_{T}(y) = d_{T^{'}}(z) + 1 dT(x)=dT(y)=dT′(z)+1,故 f ( x ) d T ( x ) + f ( y ) d T ( y ) = ( f ( x ) + f ( y ) ) ( d T ′ ( z ) + 1 ) = f ( x ) + f ( y ) + f ( z ) d T ′ ( z ) \begin{aligned} f(x) d_{T}(x) + f(y) d_{T}(y) &= (f(x) + f(y))(d_{T^{'}}(z) + 1) \\ &= f(x) + f(y) + f(z) d_{T^{'}}(z) \end{aligned} f(x)dT(x)+f(y)dT(y)=(f(x)+f(y))(dT′(z)+1)=f(x)+f(y)+f(z)dT′(z)
- 由此可知, B ( T ) = B ( T ′ ) + f ( x ) + f ( y ) B(T) = B(T^{'}) + f(x) + f(y) B(T)=B(T′)+f(x)+f(y)
- 若 T ′ T^{'} T′表示的字符集 C ′ C^{'} C′的前缀码不是最优的,则有 T ′ ′ T^{''} T′′表示的 C ′ C^{'} C′的前缀码使得 B ( T ′ ′ ) < B ( T ′ ) B(T^{''}) < B(T^{'}) B(T′′)<B(T′),由于 z z z被看作 C ′ C^{'} C′中的一个字符,故 z z z在 T ′ ′ T^{''} T′′中是一树叶,若将 x x x和 y y y加入树 T ′ ′ T^{''} T′′中作为 z z z的儿子,则得到表示字符集 C C C的前缀码的二叉树 T ′ ′ ′ T^{'''} T′′′,且有 B ( T ′ ′ ′ ) = B ( T ′ ′ ) + f ( x ) + f ( y ) < B ( T ′ ) + f ( x ) + f ( y ) = B ( T ) B(T^{'''}) = B(T^{''}) + f(x) + f(y) < B({T^{'}}) + f(x) + f(y) = B(T) B(T′′′)=B(T′′)+f(x)+f(y)<B(T′)+f(x)+f(y)=B(T),这与 T T T的最优性矛盾,故 T ′ T^{'} T′表示的 C ′ C^{'} C′的前缀码是最优的
总结
- 由贪心选择性质和最优子结构性质立即推出哈夫曼算法是正确的,即哈夫曼算法产生 C C C的一棵最优前缀编码树
Python实现
from heapq import heappop, heappush
from collections import defaultdictclass HuffmanNode:def __init__(self, char, freq, left=None, right=None):self.char = char # 节点代表的字符self.freq = freq # 节点对应字符的频率self.left = left # 左子节点self.right = right # 右子节点def __lt__(self, other):return self.freq < other.freqdef build_frequency_table(text):frequency_table = defaultdict(int) # 存储字符频率的字典, 默认值为 0for char in text:frequency_table[char] += 1 # 统计字符频率return frequency_tabledef build_huffman_tree(frequency_table):priority_queue = [] # 存储 Huffman 节点的优先队列(最小堆)for char, freq in frequency_table.items():node = HuffmanNode(char, freq)heappush(priority_queue, node) # 将每个字符的频率作为优先级, 构建最小堆while len(priority_queue) > 1:left_node = heappop(priority_queue) # 弹出频率最小的节点作为左子节点right_node = heappop(priority_queue) # 弹出频率次小的节点作为右子节点parent_freq = left_node.freq + right_node.freq # 父节点的频率是左右子节点频率之和parent_node = HuffmanNode(None, parent_freq, left_node, right_node)heappush(priority_queue, parent_node) # 将父节点插入优先队列return heappop(priority_queue) # 返回最后剩余的根节点def generate_codes(node, current_code, codes):if node.char:codes[node.char] = current_code # 如果节点代表一个字符, 将字符和对应的编码存入字典else:generate_codes(node.left, current_code + '0', codes) # 递归生成左子树编码, 将当前编码加上 '0'generate_codes(node.right, current_code + '1', codes) # 递归生成右子树编码, 将当前编码加上 '1'def huffman_encoding(text):frequency_table = build_frequency_table(text) # 构建字符频率表huffman_tree = build_huffman_tree(frequency_table) # 构建 Huffman 树codes = {} # 存储字符和对应的 Huffman 编码的字典generate_codes(huffman_tree, '', codes) # 生成 Huffman 编码encoded_text = ''.join(codes[char] for char in text) # 将文本编码为 Huffman 编码return encoded_text, huffman_treedef huffman_decoding(encoded_text, huffman_tree):decoded_text = ''current_node = huffman_treefor bit in encoded_text:if bit == '0':current_node = current_node.left # 如果是 '0', 移动到左子节点else:current_node = current_node.right # 如果是 '1', 移动到右子节点if current_node.char: # 如果当前节点代表一个字符decoded_text += current_node.char # 将字符添加到解码文本中current_node = huffman_tree # 重置当前节点为根节点return decoded_texttext = 'Hello, Huffman!'
print(f'原始文本: {text}')encoded_text, huffman_tree = huffman_encoding(text)
print(f'编码后的文本: {encoded_text}')decoded_text = huffman_decoding(encoded_text, huffman_tree)
print(f'解码后的文本: {decoded_text}')
原始文本: Hello, Huffman!
编码后的文本: 01110100010010100010110110111000111111000110111001001
解码后的文本: Hello, Huffman!
时间复杂性
- 算法用最小堆实现优先队列 Q Q Q,初始化优先队列需要 O ( n ) O(n) O(n)计算时间,由于最小堆的删除结点和插入结点运算均需 O ( log n ) O(\log{n}) O(logn)时间, n − 1 n - 1 n−1次的合并共需要 O ( n log n ) O(n \log{n}) O(nlogn)计算时间
- 因此,关于 n n n个字符的哈夫曼算法的计算时间为 O ( n log n ) O(n \log{n}) O(nlogn)
相关文章:

【贪心算法】哈夫曼编码Python实现
文章目录 [toc]哈夫曼编码不同编码方式对比前缀码构造哈夫曼编码哈夫曼算法的正确性贪心选择性质证明 最优子结构性质证明 总结 Python实现时间复杂性 哈夫曼编码 哈夫曼编码是广泛用于数据文件压缩的十分有效的编码方法,其压缩率通常为 20 % 20\% 20%到 90 % 90\%…...

【RAG 博客】RAG 应用中的 Routing
Blog:Routing in RAG-Driven Applications ⭐⭐⭐⭐ 根据用户的查询意图,在 RAG 程序内部使用 “Routing the control flow” 可以帮助我们构建更实用强大的 RAG 程序。路由模块的关键实现就是一个 Router,它根据 user query 的查询意图&…...

鸿蒙ArkUI:【编程范式:命令式->声明式】
命令式 简单讲就是需要开发用代码一步一步进行布局,这个过程需要开发全程参与。 开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 Objective-C ObjectiveC 复制代码 UIView *cardView …...

【练习2】
1.汽水瓶 ps:注意涉及多个输入,我就说怎么老不对,无语~ #include <cmath> #include <iostream> using namespace std;int main() {int n;int num,flag,kp,temp;while (cin>>n) {flag1;num0;temp0;kpn;while (flag1) {if(kp<2){if(…...

oracle 新_多种块大小的支持9i
oracle 新_多种块大小的支持 conn sys/sys as sysdba SHOW PARAMETER CACHE ALTER SYSTEM SET DB_CACHE_SIZE16M; ALTER SYSTEM SET DB_4K_CACHE_SIZE8M; CREATE TABLESPACE K4 DATAFILE F:\ORACLE\ORADATA\ZL9\K4.DBF SIZE 2M BLOCKSIZE 4K; CREATE TABLE SCOTT.A1 TABLESP…...

Collections工具类
类java.util.Collections提供了对Set、List、Map进行排序、填充、查找元素的辅助方法。 方法名说明void sort(List)对List容器内的元素排序,排序规则是升序void shuffle(List)对List容器内的元素进行随机排列void reverse(List)对List容器内的元素进行逆序排列void…...
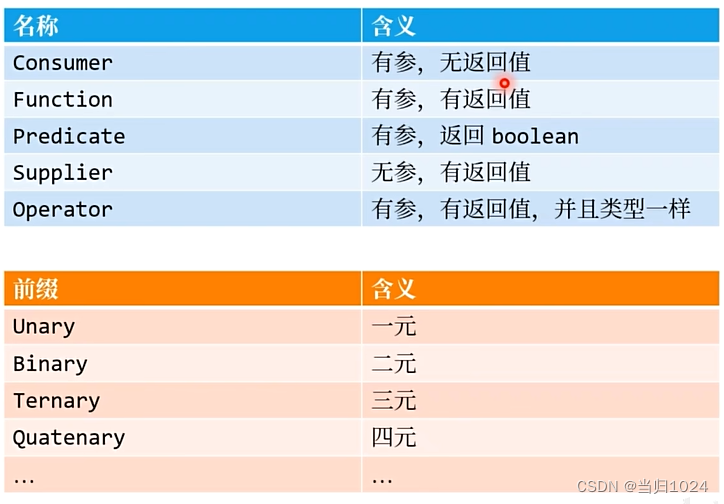
java-函数式编程-jdk
背景 函数式接口很简单,但是不是每一个函数式接口都需要我们自己来写jdk 根据 有无参数,有无返回值,参数的个数和类型,返回值的类型 提前定义了一些通用的函数式接口 IntPredicate 参数:有一个,类型是int类…...

qiankun实现微前端,vue3为主应用,分别引入vue2和vue3微应用
1、vue3主应用配置 1、安装 qiankun yarn add qiankun # 或者 npm i qiankun -S2、在主应用中注册微应用 import { registerMicroApps, start } from "qiankun" const apps [{ name: vue2App, // 应用名称 xs_yiqing_vue2entry: //localhost:8080, // vue 应用…...

写了 1000 条 Prompt 之后,我总结出了这 9 个框架【建议收藏】
如果你对于写 Prompt 有点无从下手,那么,本文将为你带来 9 个快速编写 Prompt 的框架,你可以根据自己的需求,选择任意一个框架,填入指定的内容,即可以得到一段高效的 Prompt,让 LLM 给你准确满意…...

事件代理 浅谈
事件代理是一种将事件处理委托给父元素或祖先元素来管理的技术。当子元素触发特定事件时,该事件不会直接在子元素上进行处理,而是会冒泡到父元素或祖先元素,并在那里进行处理。这样做的好处是可以减少事件处理函数的数量,提高性能…...

一对多在线教育系统,疫情后,在线教育有哪些变革?
疫情期间,全面开展的在线教育经历了从不适应到认可投入并常态化的发展过程。如何发挥在线教学优势,深度融合线上与线下教育,将在线教育作为育人方式变革动力,提升育人服务水平,是复学复课后学校教育教学面临的关键问题…...
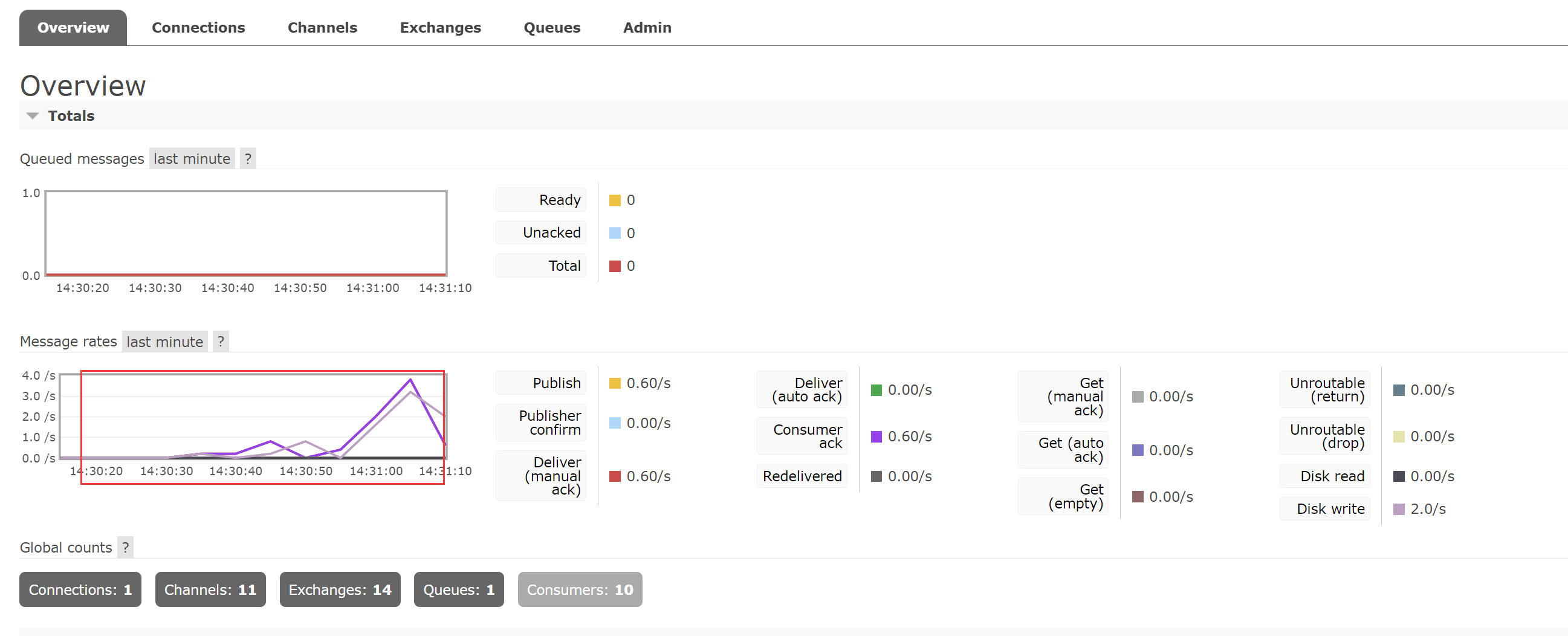
RabbitMQ(安装配置以及与SpringBoot整合)
文章目录 1.基本介绍2.Linux下安装配置RabbitMQ1.安装erlang环境1.将文件上传到/opt目录下2.进入/opt目录下,然后安装 2.安装RabbitMQ1.进入/opt目录,安装所需依赖2.安装MQ 3.基本配置1.启动MQ2.查看MQ状态3.安装web管理插件4.安装web管理插件超时的解决…...

JUC下的BlockingQueue详解
BlockingQueue是Java并发包(java.util.concurrent)中提供的一个接口,它扩展了Queue接口,增加了阻塞功能。这意味着当队列满时尝试入队操作,或者队列空时尝试出队操作,线程会进入等待状态,直到队列状态允许操作继续。这…...

ChatGPT理论分析
ChatGPT "ChatGPT"是一个基于GPT(Generative Pre-trained Transformer)架构的对话系统。GPT 是一个由OpenAI 开发的自然语言处理(NLP)模型,它使用深度学习来生成文本。以下是对ChatGPT进行理论分析的几个主…...

算法提高之魔板
算法提高之魔板 核心思想:最短路模型 将所有状态存入队列 更新步数 同时记录前驱状态 #include <iostream>#include <cstring>#include <algorithm>#include <unordered_map>#include <queue>using namespace std;string start&qu…...
服务器内存占用不足会怎么样,解决方案
在当今数据驱动的时代,服务器对于我们的工作和生活起着举足轻重的作用。而在众多影响服务器性能的关键因素当中,内存扮演着极其重要的角色。 服务器内存,也称RAM(Random Access Memory),是服务器核心硬件部…...

elasticsearch文档读写原理大致分析一下
文档写简介 客户端通过hash选择一个node发送请求,专业术语叫做协调节点 协调节点会对document进行路由,将请求转发给对应的primary shard primary shard在处理完数据后,会将document 同步到所有replica shard 协调节点将处理结果返回给…...

1 开发环境
开发环境(platformio python arduino框架)的搭建可以参考b站upESP32超详细教程-使用VSCode(基于Arduino框架)哔哩哔哩bilibili 这里推荐离线安装esp32库文件,要不然要等很久(b站教程很多) 搭…...

云视频,也称为视频云服务,是一种基于云计算技术理念的视频流媒体服务
云视频,也称为视频云服务,是一种基于云计算技术理念的视频流媒体服务。它基于云计算商业模式,为视频网络平台服务提供强大的支持。在云平台上,所有的视频供应商、代理商、策划服务商、制作商、行业协会、管理机构、行业媒体和法律…...

[Vision Board创客营]--使用openmv识别阿尼亚
文章目录 [Vision Board创客营]使用openmv识别阿尼亚介绍环境搭建训练模型上传图片生成模型 使用结语 [Vision Board创客营]使用openmv识别阿尼亚 🚀🚀五一和女朋友去看了《间谍过家家 代号:白》,入坑二刺螈(QQ头像也换…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
